基于Romax的圆柱齿轮微观修形分析研究

山东蓬翔汽车有限公司技术中心 山东烟台 265607

齿轮的啮合强度，除了受到齿轮本身模数、齿数、压力角以及配对安装距等宏观参数影响外，还受到微观几何参数的影响，其中齿轮修形就是一个重要的影响因素。轴、轴承等在受载情况下会发生变形，将导致两配对啮合的齿轮轮齿间因错位出现啮合偏载，引起振动增加噪声，使齿轮的寿命降低。此时传动系统总成的整体布置已经定型，无法再通过更改轴、轴承、齿轮的宏观参数来降低接触应力，此时可以尝试调整齿轮的微观几何参数，即通过齿轮修形来降低或抵消啮合错位的影响，降低齿轮接触应力、弯曲应力和传动误差，最终提高齿轮性能。

本文以重型货车中桥主减速器的主、从动圆柱齿轮为研究对象，通过在Romax下建立圆柱齿轮的参数化模型，对轮齿齿面修形前后的接触区域、单位载荷和端面传动误差等进行对比分析，最终得出齿面修形有助于提高齿轮传动性能。

现状分析

1.建立模型

图1所示为在Romax下对中桥主减速器圆柱齿轮传动建立完成的数字参数化模型[1]。在中桥输入轴和主动锥齿轮轴上分别安装固定有主、从动圆柱齿轮。除此之外，两根传动轴上还包含了对应的圆锥滚子轴承、圆柱滚子轴承和中桥输入突缘，各零部件参数及工作定位均按照中桥主减速器总成图样状态确定。建模后齿轮组的具体参数见表1。其中模数、齿数、压力角、螺旋角、齿宽以及工作中心距等各项具体参数全部包含在内。

图1 中桥主减速器圆柱齿轮传动模型

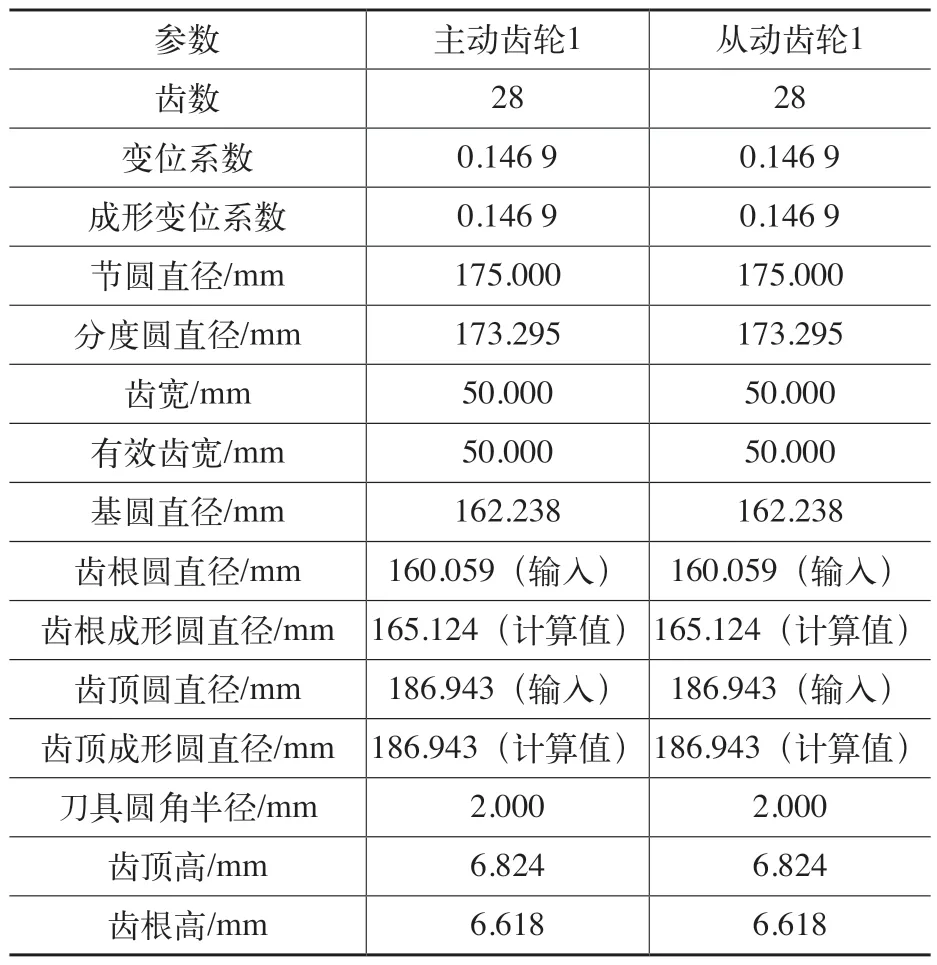
表1 主、从动圆柱齿轮组参数表

2.输入载荷

按照QC/T533汽车驱动桥台架试验方法输入载荷参数，包括输入转矩、转速、持续时间和工作温度，各项参数全部按照载荷谱功率流参数（见表2）执行。

表2 载荷谱功率流参数

输入扭矩、输入转速与总成功率存在如下关系

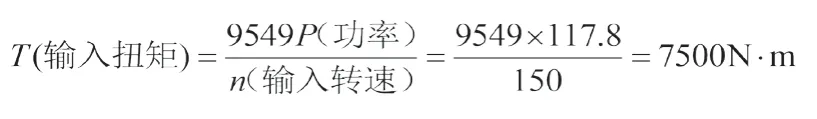
3.运行结果

从啮合运行结果（见表3）来看，受载情况明显不够理想。在现有结构状态和载荷参数下，圆柱齿轮组的接触应力和弯曲应力明显偏大，计算得到的接触和弯曲应力安全系数分别为0.9511和1.043，数值偏低。

如图2所示为齿轮端面传动线性误差曲线[3]，计算得到的误差值为41.43μm，此数值的大小为决定齿轮传动过程中振动大小的核心因素，数值越大，产生振动越大，这便是引起齿轮啸叫的原因[4]。

表3 啮合运行结果

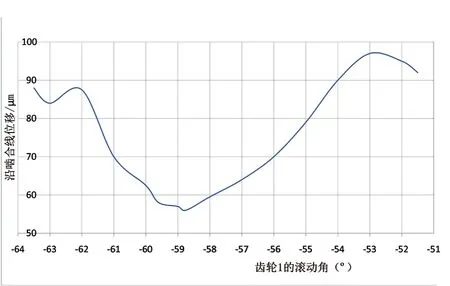
图2 传动线性误差

如图3所示为分析得到的齿轮单位线载荷的等高线云图，其上精确计算得出了轮齿齿面的单位长度载荷与滚动角和齿面距离的位置关系。如图4所示为该单位线载荷在齿轮啮合齿上的位置分布情况。至此就可以清晰直观地看到该对互相啮合的轮齿齿面上的接触斑情况。可以得出结论：当前情况下齿面上存在严重的偏载。

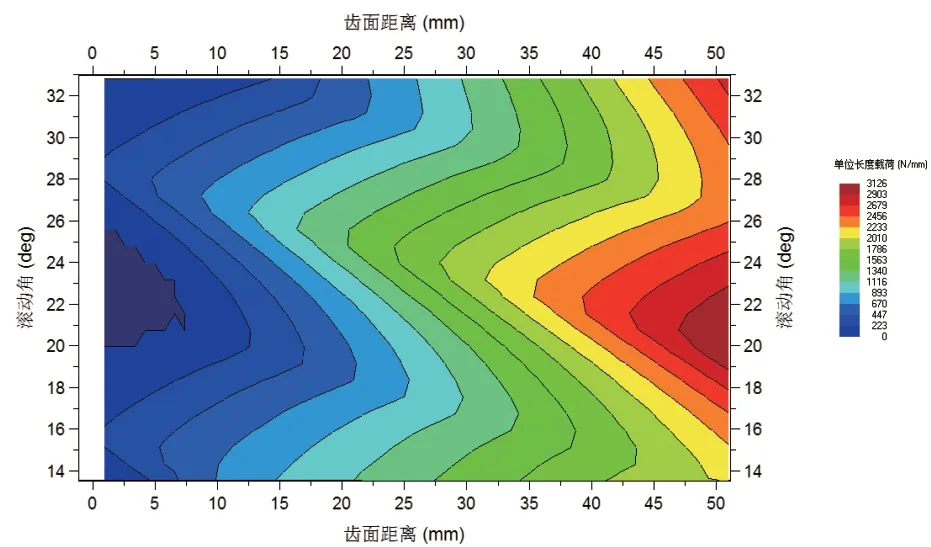
图3 单位线载荷等高线云图

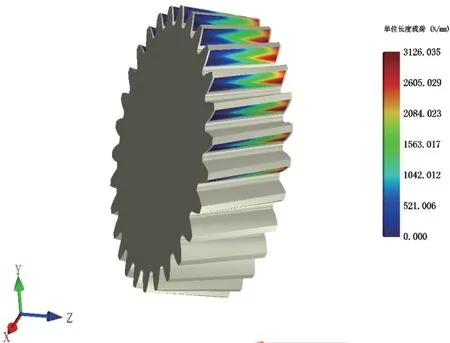
图4 啮合传动接触斑

轮齿修形改进

齿轮修形指的是对齿轮几何参数的微观调整，具体包括齿向修形和渐开线鼓形。齿向修形是指对轮齿沿着齿宽方向进行几何参数调整，包括齿向鼓形（见图5）和齿向斜度修正；渐开线修形是指调整齿廓方向的几何参数，降低由于轮齿弹性形变、制造和装配误差的影响[2]。

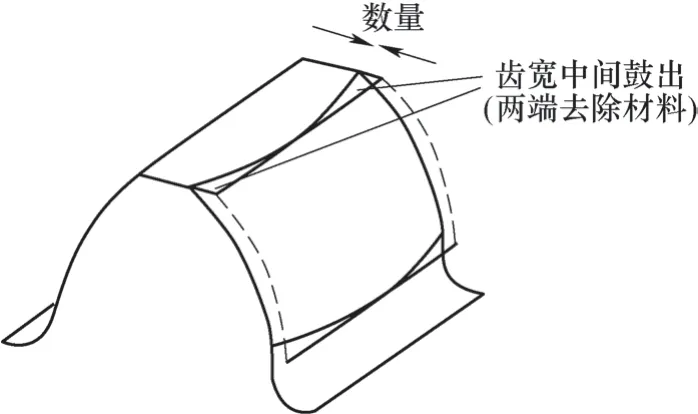
图5 齿向鼓形

1.修形参数

图6所示为轮齿修形前的齿面形状，可以看到，无论是齿向方向还是渐开线方向，其基节累计误差均为初始值，即齿向鼓形、齿向斜度以及渐开线鼓形等数值均为0[5]。

修形参数的最佳选择要权衡几项修形参数综合考虑，可通过全阶乘方法、蒙特卡洛法或遗传算法计算得出（本文不予详述），也可通过经验数据进行尝试，最后从几种方案中择优选择[6]。

图6 修形前齿面形状

图7所示即为最终择优选择的具体修形参数数据，其中包含有齿向鼓形、齿向斜度和渐开线鼓形。除此之外，还包括在齿顶位置去除材料的齿顶修缘。

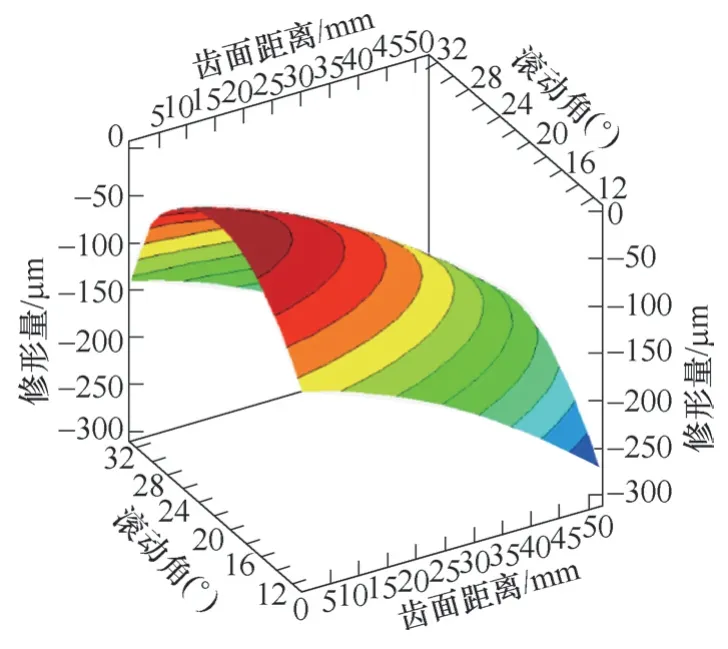
图7 修形后齿面形状

2.修形后运行结果

图8为修形后的齿轮端面传动线性误差曲线，计算得到的误差值为9.32μm，相比修形前的41.43μm降低了77.5%。

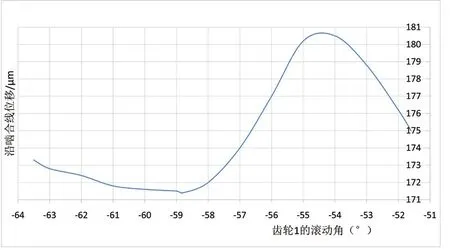
图8 传动线性误差（修形后）

图9所示为修形后计算得到的齿轮单位线载荷的等高线云图，图10为齿面上的啮合接触斑情况。由此可以清楚地看到，修形后，啮合接触斑由齿面边缘移到了正中，啮合接触情况大大改观。

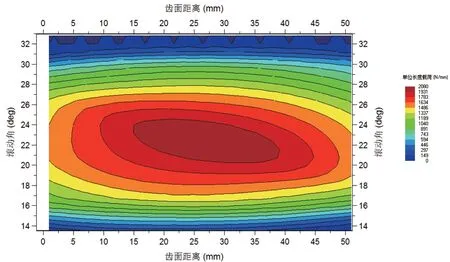
图9 修形后单位线载荷等高线云图

图10 修形后啮合传动接触斑

修形后，不仅原齿面啮合接触的严重偏载问题得到解决，传动线性误差也得到大幅提升，而且轮齿的接触应力和弯曲应力也明显降低。从表4的修行后啮合运行结果可以看到，接触和弯曲应力安全系数分别提升至1.272和1.617，分别提升了33.7%和55%。

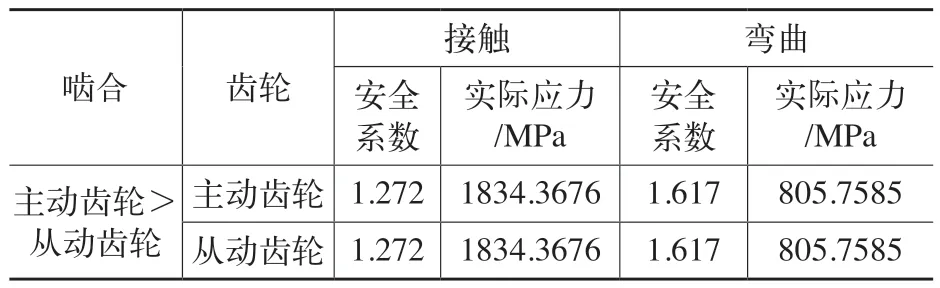
表4 修行后啮合运行结果

实际应用

一直以来，圆柱齿轮的市场故障始终居高不下，究其原因，除了整车运行工况、齿轮本身制造质量等因素外，在产品设计环节的微观几何参数不受重视，也是一个重要原因。近两年通过CAE理论分析，业内人士逐渐认识到齿轮微观修形的重要价值，并逐渐将其应用于生产实际。

结语

基于Romax运用数字模拟的方法，通过对圆柱齿轮微观修形前后的受载情况进行直接对比，让人清晰明了地看到了齿轮修形对于改善齿轮传动效果的重要性，解决了以往齿轮传动中大偏载、强振动、高噪声、短寿命的问题，取得了良好的效果。