基于视觉的标准渐开线直齿圆柱齿轮齿形缺陷检测
豆永坤 王洪申 张翔宇 徐鹏飞
(兰州理工大学机电工程学院 甘肃 兰州 730050)
0 引 言
标准渐开线直齿圆柱齿轮应用广泛,齿轮轮齿对于齿轮传动的平稳性起着关键性作用。齿轮的主要失效形式也集中在轮齿上,如:轮齿折断、齿面磨损、齿面点蚀等,这些失效形式都会对齿轮轮齿的轮廓造成影响。因此,可以通过对齿轮轮齿轮廓的检测,检测一个齿轮的轮齿是否失效;也可用来判定使用过的齿轮是否具有可继续使用性。
基于工业视觉的齿轮检测具有自动化程度高、非接触、低成本等优点。许多学者对其进行了研究,Saini等[1]借助图像处理算法与计算机视觉对塑料齿轮的缺陷进行识别;Ali等[2]应用计算机视觉的方法来改善齿轮轮廓检测的安全性和可靠性;Wang等[3]基于机器视觉设计了齿轮参数的检测系统;王文成[4]利用单个轮齿像素总数的比较方法对轮齿的缺陷进行检测;贺秋伟等[5]对微型齿轮轮齿缺陷采用图像处理技术和支持向量机的方法进行检测;杨淑莹等[6]对齿轮实际图像和设计图像采用互信息的方法进行配准,然后对两幅图像进行小波融合,基于两幅图像的重合效果,来判断齿轮产品是否合格;赵霞等[7]对齿轮的齿形误差通过建立齿形误差的图像法测量数学模型来进行检测。
本文借助Halcon软件,使用Microsoft Visual Studio 2010设计了齿轮齿型检测系统,系统结构流程如图1所示。首先对齿轮图像进行采集与预处理,对齿轮图像进行尺寸检测,获取齿轮基本参数;根据获取的参数,画出标准轮齿轮廓;然后提取待测齿轮轮齿轮廓;最后计算对应位置的实际轮齿轮廓与标准轮齿轮廓的Hausdorff距离,看是否小于设定的公差,来判定轮齿是否合格,完成对齿轮轮齿的检测。
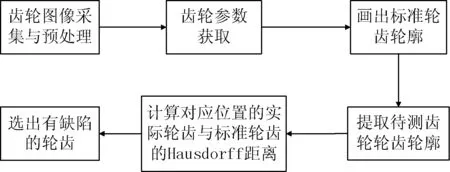
图1 系统结构流程图
1 齿轮图像采集及预处理
Halcon是德国MVtec公司开发的一套完善的标准的机器视觉算法包,拥有应用广泛的机器视觉集成开发环境。为了让使用者能在最短的时间里开发出视觉系统,其包含了一套交互式的程序设计界面HDevelop,可在其中以Halcon程序代码直接撰写、修改、执行程序,并且可以查看运行过程中的所有变量。设计完成后,可以直接输出C++等不同的程序代码,套入程序中。
如图2所示,使用HDevelop界面的菜单,运用一系列编辑的Halcon算子对图像进行处理。处理完成后,把算子以C++代码的形式导入开发的系统中。

图2 HDevelop界面
1.1 齿轮图像采集
本文采集图像所用的工业相机为西安维视MV-EM 120C工业相机,镜头分辨率为1 280×960,检测精度为0.05 mm。
使用open_framegrabber算子打开相机,grab_image_start算子对齿轮图像进行采集,得到的齿轮图像如图3所示。

图3 齿轮图像采集
1.2 齿轮图像的预处理
图像在采集和传输中会不可避免的受到噪声的污染,影响人们对图像的理解和分析处理。图像去噪的目的就是滤除噪声,减少噪声的影响。图像中主要的噪声是椒盐噪声和高斯噪声,首先使用Halcon中自带的中值滤波算子median_image对采集的齿轮图像进行处理,消除椒盐噪声的影响;再采用高斯滤波算子gauss_image,消除高斯噪声的影响。处理过的图像如图4所示。
1.3 图像分割
如式(1)所示,设原始图像为f(x,y),二值化后的图像为g(x,y),阈值为M,其中1为目标图像的值,0为背景图像的值。对图像进行二值化能够清晰地区分背景图像和目标图像。
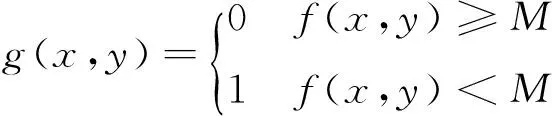
(1)
使用HDevelop界面中的灰度直方图工具,根据灰度直方图中图像灰度值分布的疏密程度,选用合适的阈值对滤波后的齿轮图像进行二值化, 齿轮图像的灰度直方图如图5(a)所示,二值化的图像如图5(b)所示。采用的算法如下:
threshold (ImageGauss, Regions, 0, 77)
其中,ImageGauss为输入的图像变量,Regions为输出的图像变量;0和77分别是选取的最小和最大灰度值。齿轮图像灰度值在0和77之间的被设定为目标图像,大于77的为背景图像。
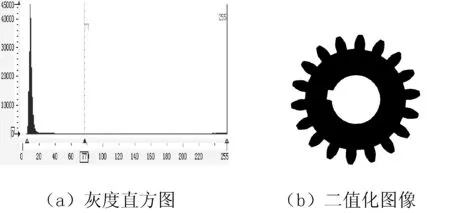
图5 图像分割
2 齿轮参数获取
二值化后的齿轮图像,虽然把目标齿轮和背景图像分别提取出来,难免会把图像中的一些杂点也当做目标区域提取了出来,因此需要使用算法把杂点滤掉,提取目标齿轮。Halcon中的connection算子可以根据区域的连通关系,把图像中的各个区域独立分开,只需要把齿轮区域提取出来即可。
而目标齿轮又是二值图像中最大的非背景区域,所以使用select_shape_std把二值图像中最大的非背景区域提取出来,也即把目标齿轮提取出来。算法如下:
select_shape_std(ConnectedRegions,SelectedRegions,′max_area′, 70)
其中,ConnectedRegions为图像中独立的各个非背景区域,SelectedRegions为选出的最大区域,即是齿轮区域。‘max_area’是最大区域参数,“70”为相似程度参数,数值越大相似程度越高,最大值为100,70为默认值。
2.1 获取齿顶圆直径和齿根圆直径
由齿轮的各个参数可以画出一个标准渐开线直齿圆柱齿轮,齿轮的渐开线齿廓形状也是由齿轮的参数决定的。可以使用Halcon中的算子获取齿轮的一些基本参数。采用的算子如下:
fill_up(SelectedRegions,RegionFillUp)
smallest_circle(RegionFillUp,OuterRow,OuterColumn,OuterRadius)
inner_circle(RegionFillUp,InnerRow,InnerColumn,InnerRadius)
fill_up算子把齿轮的内部的孔填充,以免内部的孔对参数获取造成影响;smallest_circle算子获取齿轮的齿顶圆半径和齿顶圆的中心坐标;inner_circle算子获取齿轮的齿根圆半径和齿根圆的中心坐标。其中RegionFillUp为填充内孔之后的齿轮区域,OuterRadius是获得的齿顶圆半径, (OuterRow,OuterColumn) 为齿顶圆的中心坐标,InnerRadius是获得的齿根圆半径, (InnerRow,InnerColumn) 为齿根圆的中心坐标。由da=2×OuterRadius和df=2×InnerRadius,可以得到齿轮的齿顶圆直径和齿根圆直径。
2.2 齿轮齿数、模数、分度圆直径和基圆直径的获取
(1) 根据齿根圆的中心坐标和齿根圆半径,生成一个圆区域,使得这个区域把齿根圆以内区域完全包含进去,如图6(a)所示,算子语句如下:
gen_circle(Circle,InnerRow,InnerColumn,InnerRadius)
采用下面的算子获取此圆区域的补集,如图6(b)所示。
complement(Circle,RegionComplement)
对填充齿轮区域和圆区域补集区域求交集,可以得到只包含轮齿的区域,这样可以采用相应的算法得到齿轮的齿数。得到的只包含轮齿图像如图6(c)所示。
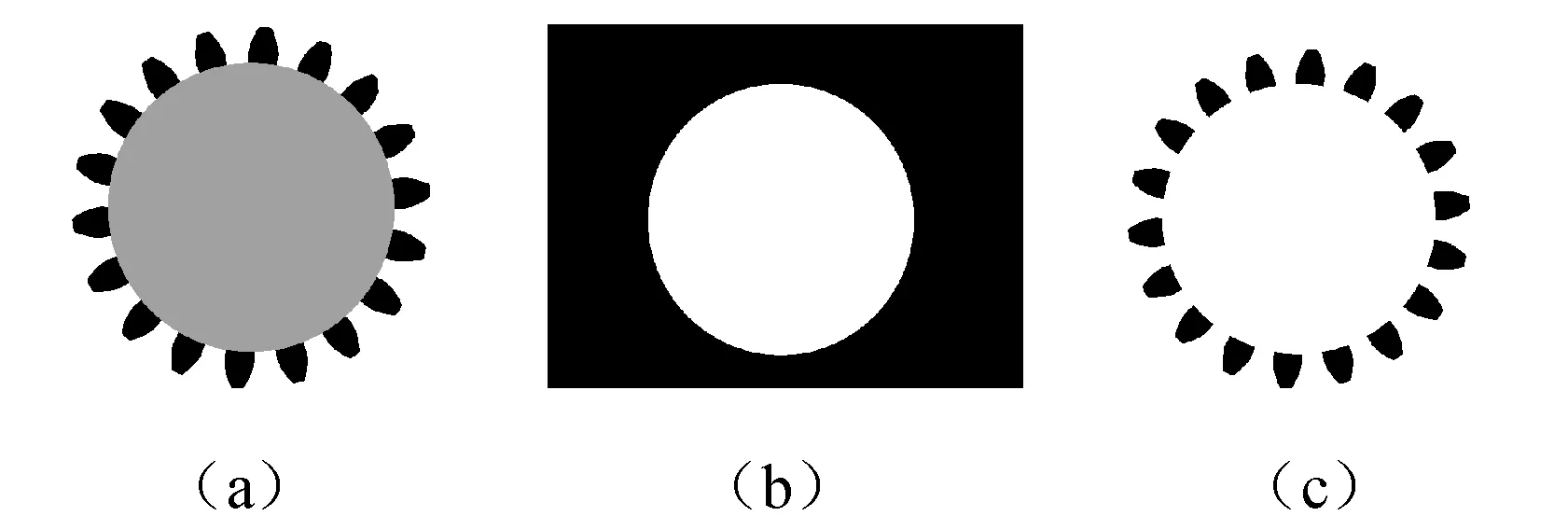
图6 提取轮齿过程
(2) 使用connection算子根据连通性把各个轮齿独立分开,再使用count_obj计算齿轮的轮齿数量,使用的算子语句如下:
connection(RegionIntersection,ConnectedDefect)
count_obj(ConnectedDefect,Z)
其中,ConnectedDefect表示根据连通性各个独立的轮齿区域,Z表示齿数。由公式m=da/(Z+2),d=mz,db=d×cosα,可以得到齿轮的模数m,分度圆直径d和基圆直径db。由齿数Z,可以得到两个轮齿中心的夹角P=360°/Z。
3 齿轮轮齿的检测
3.1 根据齿轮参数画出标准轮齿轮廓
图7为渐开线生成原理图,因为渐开线是从基圆上的点开始的,可以利用基圆上的点(x1,y1)来确定渐开线上对应的点(x,y)。图中,L为渐开线发生线,渐开线发生线L和渐开线发生线L在基圆上做纯滚动绕过的圆弧S距离相等。
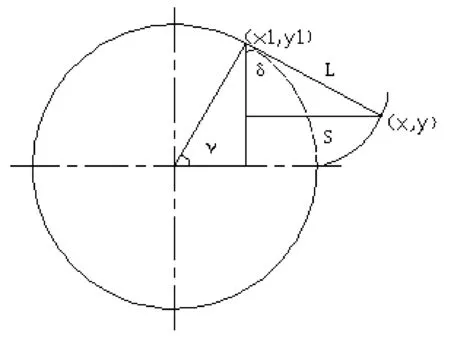
图7 渐开线生成原理图
用(x1,y1)表示(x,y)的公式如下所示:
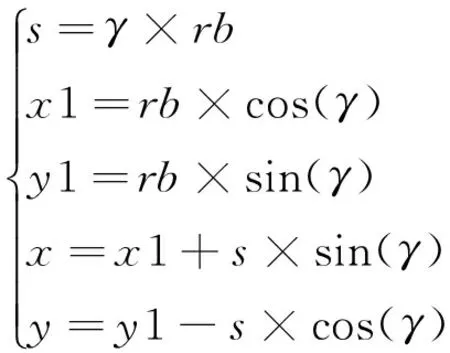
(2)
式中:rb为齿轮基圆的半径,γ为点(x1,y1)、基圆圆心连线与水平线的夹角。
基于此,以齿轮的齿顶圆中心为圆心,分别画出基圆、齿顶圆和水平位置齿轮轮齿两侧的渐开线,通过对这些轮廓求交、修剪,得到一个标准的轮齿轮廓。然后把这个轮齿轮廓以角度P顺时针旋转,得到齿轮的各个标准轮齿轮廓。处理的过程如图8所示。

图8 生成标准轮齿轮廓
3.2 获取待测齿轮的轮齿轮廓
3.2.1 对齿轮图像进行旋转
使用Halcon算子获取一个待测齿轮轮齿轮廓,并计算此轮齿轮廓与基圆的两个交点,可知这两个交点连线的中点与齿顶圆的中心连线肯定过轮齿的中心,如图9(a)所示。计算这条线与水平线的夹角为β。对待侧齿轮图像顺时针旋转β角,刚好选取的这个轮齿旋转到水平位置,如图9(b)所示。
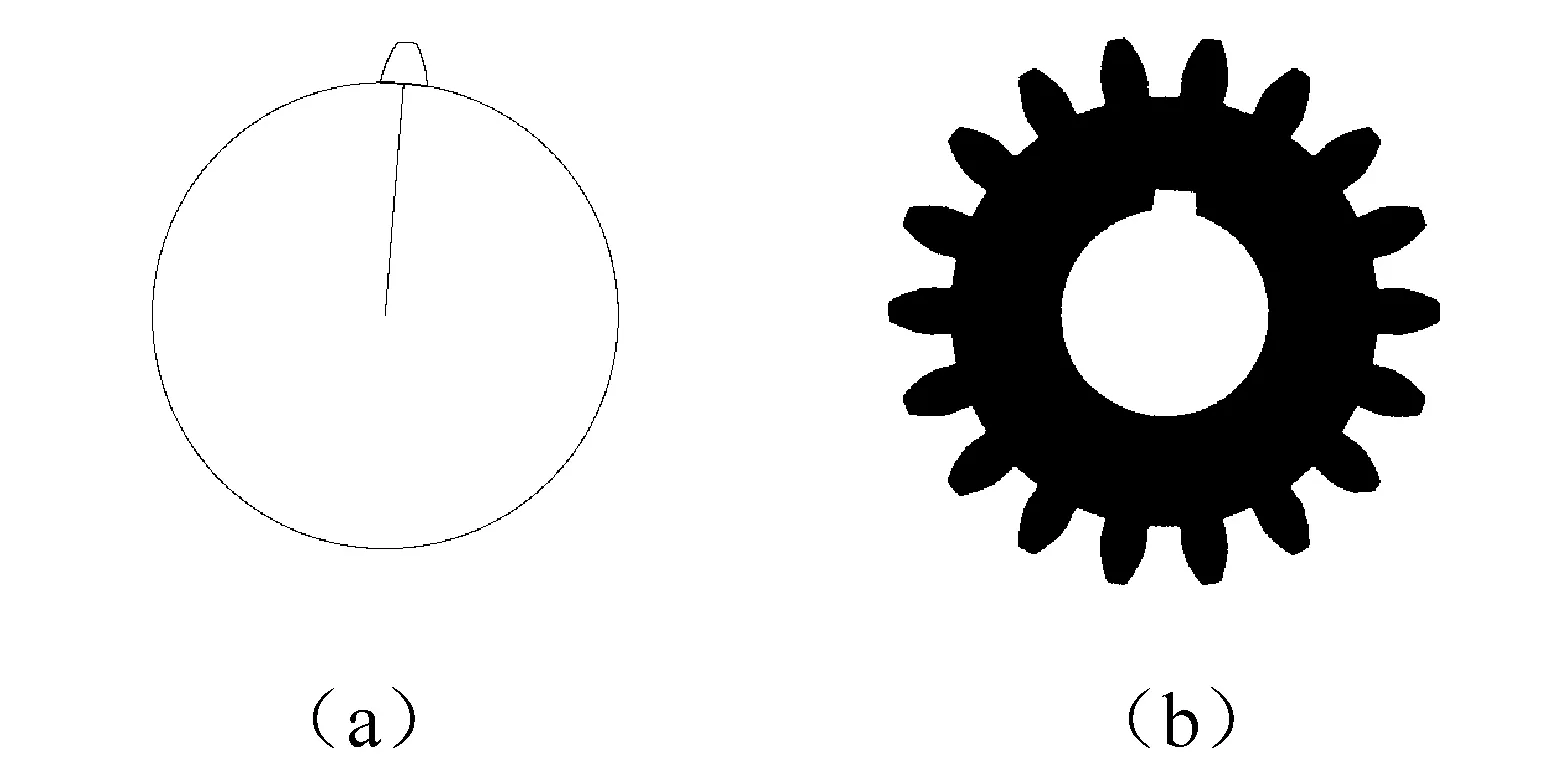
图9 齿轮图像旋转的过程
3.2.2 获取旋转后的齿轮区域的各个轮齿轮廓
获取各个轮齿的区域,然后提取其轮廓。如图10所示。
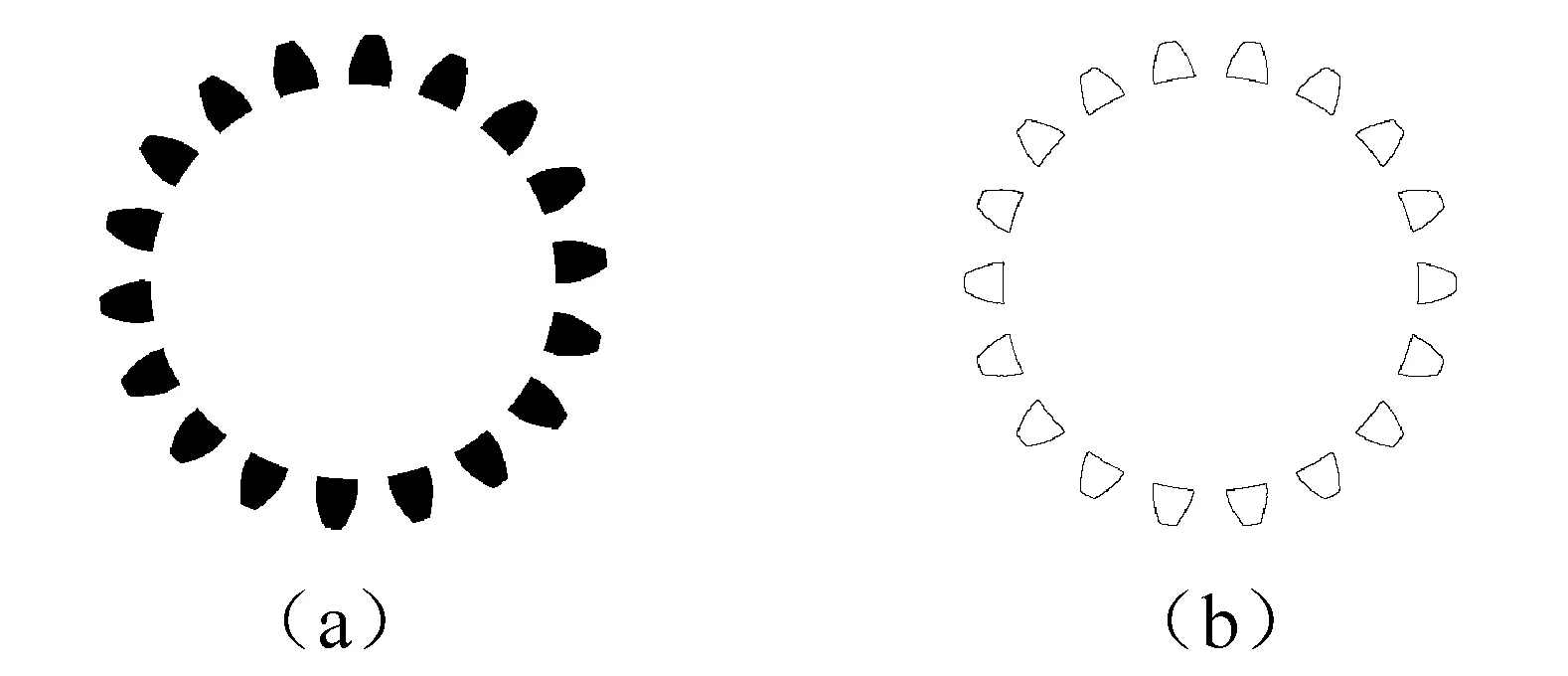
图10 提取实际齿轮的各个轮廓
使用的算子语句如下:
gen_contour_region_xld(DestRegions,Contours,′border′)
get_contour_xld(Contours,Row,Col)
其中,DestRegions为对应的轮齿区域,Contours为提取的轮齿轮廓,′border′为以“边界像素点的边界”为提取类型。Row和Col为对应轮廓的行坐标和列坐标。这里提取的齿廓是亚像素精度的轮廓。
3.3 Hausdorff距离
Hausdorff距离是用来计算两曲线间距离的一种重要的算法,常用于衡量两个集合之间差别的度量。现已广泛应用于计算几何、图像匹配、图像识别[8-11]等领域。
Hausdorff距离详述如下:平面中有两条曲线A、B,如图11所示。
图11 曲线A、B
其矢量方程可表示为:
A:A=A(a)
B:B=B(b)
平面中曲线A、B间的Hausdorff距离可分为单向和双向Hausdorff距离,其中A到B的单向Hausdorff距离是指曲线A上任意一点到曲线B的最小距离中的一个最大值[12],表示为:

式中:d(A(a),B(b))表示点a与点b间的欧几里得距离。同理,B到A的单向Hausdorff距离可表示为:
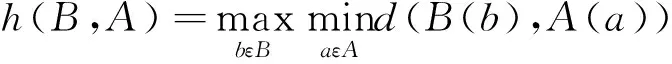
单向Hausdorff距离通常用来表示一条曲线相对于另一条曲线的最大偏差。我们取两个单向Hausdorff距离中的大者作为曲线A与B的双向Hausdorff距离,(简称Hausdorff距离)用来表示集合A、B间的最大偏差。通常表示为:
H(A,B)=max{h(A,B),h(B,A)}
3.4 齿轮轮齿缺陷的检测方法
选取一对实际齿廓与理论齿廓为例,如图12所示。其中虚线表示轮齿的实际齿廓线,实线表示轮齿的理论齿廓线。计算两条曲线的Hausdorff距离,以此值是否小于一定的公差来判定轮齿合格与否。

图12 实际齿廓与理论齿廓


图13 齿廓总偏差图形
由于灯光等因素的影响,采集的齿轮图像,与真实齿轮有所偏差。在边缘提取的过程中也会对齿轮齿廓形状造成误差,设定上述过程中造成的误差为1个像素值。
在对齿轮图像旋转过程中,选取的轮齿轮廓和基圆轮廓的两个交点取的都是整像素坐标点,同样会造成偏差,造成的偏差肯定小于1个像素值,这里取0.5个像素值。
综上所述,齿廓的总公差E等于齿廓偏差、图像采集误差与图像处理过程中造成的误差之和,得到齿廓的总公差为:
使用MFC与Halcon混合联编,设计一个基于对话框的齿轮轮齿缺陷检测系统,如图13所示。把在Halcon中使用的算子,导出并生成C++代码,套入此系统中。系统界面有采集齿轮图像、图像预处理、获取齿轮参数、画出标准渐开线轮齿轮廓、旋转齿轮图像、提取齿轮轮廓、计算Hausdorff距离及选出有缺陷的轮齿处理过程。
以实际齿廓与理论齿廓的Hausdorff距离是否小于公差E为准,来判定轮齿是否合格。不合格的轮齿将被选出,显示在图14中的图形显示窗口中。
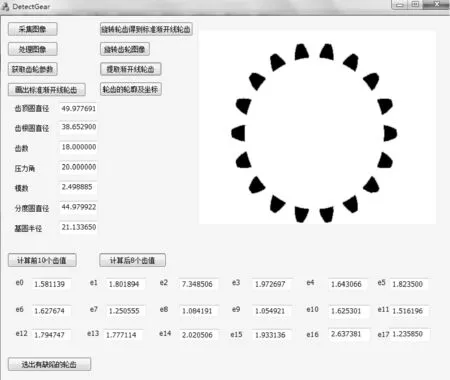
图14 轮齿检测系统界面
计算实际齿廓与理论齿廓的Hausdorff距离的程序如下:
//计算Hausdorff距离
double distance(feature_t *F1, feature_t *F2, int numA, int numB)
{
double hAB;
double hBA;
//结构体F1表示实际齿廓坐标点集合,结构体F2表示理
//论齿廓坐标点集合,numA为F1中的元素个数,numB为F2
//中的元素个数。
hAB = computeDirDistance(F1, F2, numA, numB) ;
hBA = computeDirDistance(F2, F1, numA, numB) ;
return max(hAB, hBA);
}
double computeDirDistance(feature_t *F1, feature_t *F2, int numA, int numB)
//计算单向Hausdorff距离
{
double *disA = new double[numA];
double temp;
double aB = MAX_DISTANCE;
//把一个极大值赋给aB
for (int i = 0; i < numA; i++)
{
for (int j = 0; j < numB; j++)
{
double dX = F1[i].X - F2[j].X, dY = F1[i].Y - F2[j].Y;
temp = sqrt((double)(dX*dX + dY*dY));
aB = min(temp,aB);
}//计算一个点与另一个集合各个点的欧几里得距离
disA[i] = aB;
aB = MAX_DISTANCE;
}//计算一个集合各个点与另一个集合各个点的欧几里
//得距离
sort(disA, numA);
double dis;
dis = disA[numA - 1];
delete []disA;
return dis;
}
void sort(double a[], int n)
//升序排列数组元素
{
double temp;
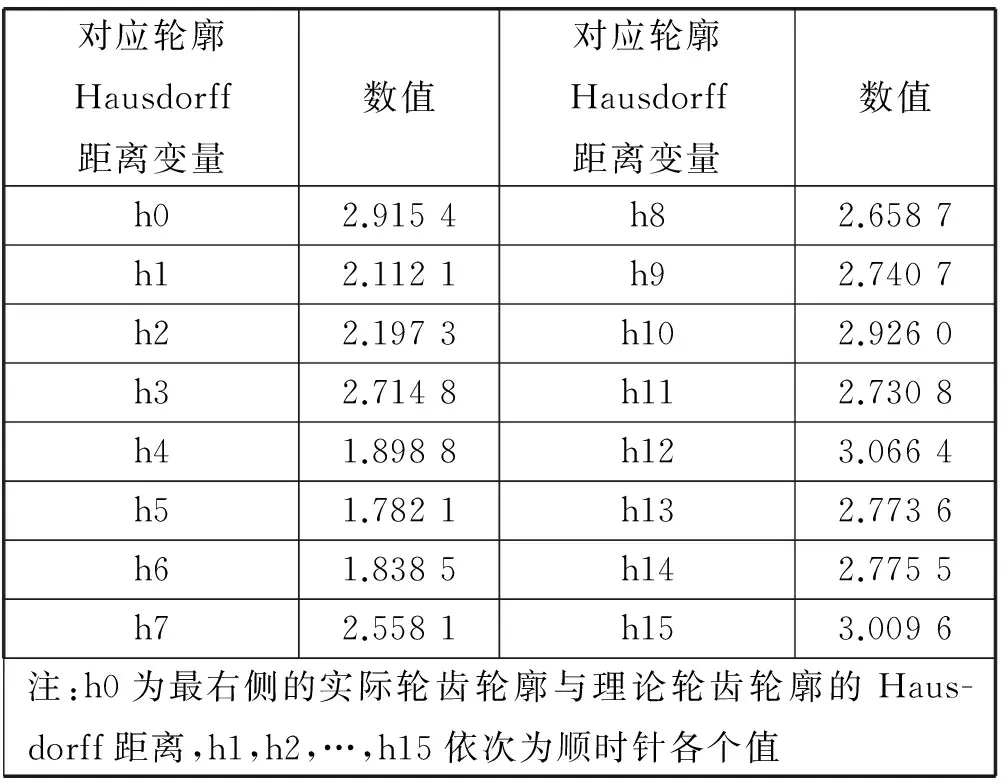
for(int i=0; i for(int j=i+1; j { if(a[i]>a[j]) { temp=a[i]; a[i]=a[j]; a[j]=temp; } } } 使用的齿轮为渐开线直齿圆柱齿轮,其中有一个轮齿已经断裂,使用本文方法对其进行检测。测得齿轮的齿数为18,模数为2.499 6,分度圆直径为44.992 8,采集的齿轮图像如图3所示。查阅第五版机械手册得:此参数下12级精度的渐开线直齿圆柱齿轮的齿廓总偏差为81 μm,因为相机精度为50 μm,换算为像素单位,齿廓总偏差为1.62个像素值。由此可以得到对应的齿廓总公差为: E=1+0.5+0.81=2.31 此齿轮对应的各个轮齿轮廓的Hausdorff距离如表1所示。 表1 各个轮齿轮廓Hausdorff距离 续表1 选出不合格的轮齿,如图15所示,黑色轮齿即为不合格轮齿。 图15 选出有缺陷的轮齿 图16为不合格的轮齿实际齿廓线与理论齿廓线。其中虚线表示轮齿的实际齿廓线,实线表示轮齿理论齿廓线,从图中可以看出断齿被选出来。 图16 有缺陷的轮齿的轮廓比较图 齿轮为使用过一段时间的渐开线直齿圆柱齿轮,经检测齿轮的齿数为16,模数为1.989 3,分度圆直径为31.828 8 mm,如图17所示。查阅第五版机械手册得:此参数下12级精度的渐开线直齿圆柱齿轮的齿廓总偏差为58 μm,换算为像素单位,齿廓总偏差为1.16个像素值。由此可以得到对应的齿廓总公差为: E=1+0.5+0.58=2.08 图17 齿轮图像 齿轮对应的各个轮齿轮廓的Hausdorff距离如表2所示。 表2 各个轮齿轮廓Hausdorff距离 选出不合格的轮齿,如图18所示,黑色轮齿即为不合格轮齿,可以看到有一半以上的轮齿已经损坏。 图18 选出有缺陷的轮齿 图19为从图18中选出的两对不合格的轮齿实际齿廓线与理论齿廓线。其中虚线表示轮齿的实际齿廓线,实线表示轮齿的理论齿廓线。 图19 有缺陷的轮齿的轮廓比较图 从上述的两个检测实例中可以看出,使用本算法可以较好地检测出标准渐开线直齿圆柱齿轮断齿缺陷和轮齿磨损。 本文借助Halcon,利用图像处理算法提取标准渐开线直齿圆柱齿轮实际轮齿轮廓。根据齿轮的基本参数画出标准的渐开线轮齿轮廓,并计算两者的Hausdorff距离,以其是否小于设定的公差,来判定齿轮轮齿是否合格。经过对实际齿轮的检测,可以看出,此方法可以很好地检测出有缺陷的齿轮轮齿。 由于是与标准轮廓相比较,本文算法能够较准确地检测出标准渐开线直齿圆柱齿轮轮齿表面的缺陷。其适用于对流水线上有缺陷的齿轮进行识别,也可以对使用过的齿轮进行检测,看是否有重用的价值。根据不同类型齿轮的特点,可以通过修改相应的处理过程,应用于对其他类型齿轮轮齿的检测。 [1] Saini P,Anand M R.Identification of Defects in Plastic Gears Using Image Processing and Computer Vision:A Review[J].International Journal of Engineering Research,2014,3(2):94-99. [2] Ali M H,Kurokawa S,Uesugi K.Application of machine vision in improving safety and reliability for gear profile measurement[J].Machine Vision & Applications,2014,25(6):1549-1559. [3] Wang Wencheng,Guan Fengnian,Ma Shiyong,et al.Measurement System of Gear Parameters Based on Machine Vision[J].Measure and Control,2015,48(8):242-248. [4] 王文成.基于Halcon的齿轮缺陷检测系统设计[J].机械传动,2014,38(9):60-62,98. [5] 贺秋伟,王龙山,于忠党,等.基于图像处理和支持向量机的微型齿轮缺陷检测[J].吉林大学学报(工学版),2008,38(3):565-569. [6] 杨淑莹,任翠池,张成,等.基于机器视觉的齿轮产品外观缺陷检测[J].天津大学学报(自然科学与工程技术版),2007,40(9):1111-1114. [7] 赵霞,毛建东.齿轮齿形误差图像测量方法的研究[J].机床与液压,2009,37(6):124-128. [8] Chen X D,Ma W,Xu G,et al.Computing the Hausdorff distance between two B-spline curves[J].Computer-Aided Design,2010,42(12):1197-1206. [9] Bai Y B,Yong J H,Liu C Y,et al.Polyline approach for approximation Hausdorff distance between plannar free-form curves[J].Computer-Aided Design,2011,43(6):687-698. [10] 郭桂旭,惠斌,冯剑.基于改进Hausdorff距离的分层景象匹配算法[J].计算机应用研究,2014,31(12):3837-3840. [11] 杨学文,冯志全,黄忠柱,等.结合手势主方向和类-Hausdorff距离的手势识别[J].计算机辅助设计与图形学学报,2016,28(1):75-81. [12] Alt H,Scharf L.Computing the Hausdorff Distance between Curved Objects[J].International Journal of Computational Geometry & Applications,2008,18(4):307-320.4 应用实例
4.1 断齿的检测




4.2 磨损齿轮轮齿的检测


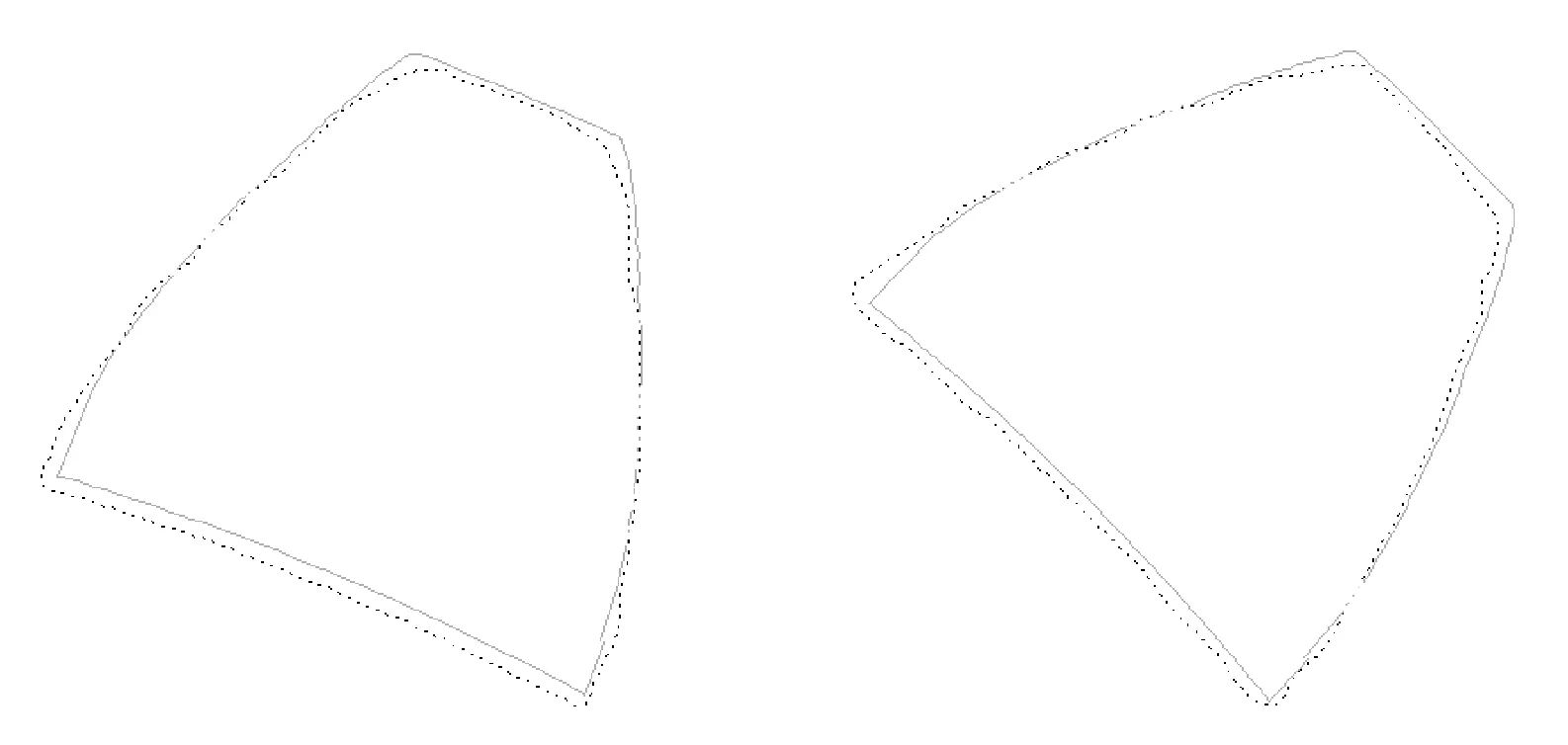
5 结 语

