有限视野下渐开线齿廓测量的坐标系校准*

杨叶茜，王建华，商执亿

(西安工业大学 机电工程学院，西安 710021)

采用光学法测量齿轮齿廓，由于测量范围和测量精度的矛盾，在有限视野下可获得高精度的齿廓数据点，但因测量视野限制导致无法准确地获得被测齿轮回转中心的位置。采用旁置式测量机测量大齿轮的齿廓，同样可获得高精度的齿廓数据点，但仍无法准确地将获得的数据点转换到以被测齿轮回转中心为原点的工件坐标系上。

由于坐标系建立不准确，直接影响齿廓测量结果的准确性，准确地将测量机的坐标原点建立在被测齿轮回转轴线上，是高精度齿廓测量的必要条件。为准确地建立测量坐标系，诸多学者开展相关研究。文献[1]提取齿轮内孔亚像素边缘轮廓的坐标点，利用最小二乘原理，给出齿轮中心坐标作为测量基准。文献[2-3]提出一种用三个已知直径的圆环获取齿轮中心孔端面圆心的方法，将此圆心作为测量渐开线齿廓和径向圆跳动的基准。文献[1-3]均能给出准确的坐标系，但获得坐标系的过程需要测得整个齿轮端面数据，位于被测齿廓上的测量点仅是整个端面测量点的一小部分，被测齿轮的直径如不是足够小，则无法获得高精度的齿廓数据。文献[4-5]根据标定圆盘上提取的一段短圆弧的坐标点，采用半径约束最小二乘圆，求解圆弧中心坐标建立坐标系。该方法虽能有效提高坐标系建立精度，但总是存在一定量的坐标系建立误差。文献[6-9]利用激光跟踪仪，通过建立被测齿轮的端平面、基准轴线以及旁置式测量机的坐标系，确定被测齿轮和旁置式测量机的位置，建立坐标转换关系。文献[10]提出将标准量块放置于被测齿轮上部空间适当位置，得到标准量块的一个测量面中心点位置后，调整回转平台180°，得到另一个测量面中心点位置，通过两个中心点位置计算齿轮回转中心位置，以此位置作为原点建立坐标系。然而，文献[6-10]所述方法均存在不同程度的坐标系建立误差。文献[11-12]建立在已知基圆半径条件下的非线性最小二乘方程，通过多条齿廓测量坐标数据求解基圆圆心坐标。该方法同样存在与文献[4-5]类似的问题。

为有效减小或消除坐标系建立误差对齿廓测量精度的影响，文中通过测量渐开线样板验证坐标系建立的准确性。如存在坐标系建立误差，可根据渐开线样板的测量数据，求出渐开线参数，得到坐标系建立误差，进而实现测量坐标系的校准。

1 渐开线参数的求解模型与算法

1.1 渐开线参数的分析

如图1所示，在所建立的测量坐标系中，测取渐开线样板坐标(xi,yi)。对应齿廓总偏差Fα的计算为

(1)

式中：Ei为齿廓在每个测量点的偏差；rb为渐开线样板基圆半径的检定值；中间变量λi是展开角;ψ为渐开线在测量坐标系中的起始角。

图1 渐开线样板坐标

如评定结果大于样板检定值，说明含有坐标系建立误差，需要对测量坐标系进行修正。假设在X轴方向上的坐标系建立误差为A，在Y轴方向上的坐标系建立误差为B，齿廓偏差Ei的计算发生变化为

(2)

基圆圆心坐标(A,B)是待求解的渐开线参数。分析式(1)和式(2)可知起始角ψ若不准确，虽不影响齿廓偏差Ei的评定结果，但会影响采用最小二乘法求解基圆圆心坐标(A,B)的求解结果，起始角ψ需作为待求解的渐开线参数。

1.2 求解模型与算法

文中提出基于齿廓偏差Ei平方和最小的原则，建立求解基圆圆心坐标(A,B)和起始角ψ的最小二乘模型，可得最小二乘模型的目标函数为

(3)

对函数最小值求解，一般令被求函数偏导数为零，求出未知参数带回被求函数，得到被求函数最小值。令P的各个偏导数为0，可得方程组，如式(4)，对此方程组求解，可获得渐开线参数的最优解Xk，最优解Xk就是坐标系建立误差为

Fm(Xk)=0,(m=1,2,3)。

(4)

目标函数是无约束非线性优化函数，所得到的式(4)是非线性的方程组，一般是将其线性化再求解。将齿廓偏差Ei线性化，线性化后的齿廓偏差Ei为

Ei=fA·A+fB·B+fψ·ψ+f0，

(5)

f0=Ei|X0-A0·fA-B0·fB-ψ0·fψ；

X0=(A0,B0,ψ0)T。

其中fA、fB、fψ分别为齿廓偏差Ei的3个偏导数在X0处的值;f0为齿廓偏差Ei线性化后的所有常数项；X0为迭代初值。假设坐标系建立误差属于小误差，在小误差条件下，可取渐开线参数的初值为零。

齿廓偏差Ei线性化后，非线性式(4)则转换为式(6)所示的线性方程组。

M·Xk=b，

(6)

式中：

一般情况下，该式(6)是病态的。其病态程度用系数矩阵M的条件数cond(M)∞来表示，条件数cond(M)∞愈大，方程组的病态程度愈严重。对系数矩阵M分析可知降低系数矩阵M的阶数，即减少待求渐开线参数的个数，条件数cond(M)∞就会显著减小。

比较基圆圆心坐标(A,B)和起始角ψ，可得将起始角ψ作为已知参数，条件数cond(M)∞最小，这时式(6)的系数矩阵M变为2阶矩阵。随着给定起始角ψ的不同，求解2阶矩阵，得到不同的基圆圆心坐标(A,B)，以齿廓总偏差Fα最小为优化目标，求解渐开线参数的最优解Xk。这样就将3阶病态矩阵的求解，转化成2阶矩阵和1维优化算法的求解。

2 渐开线参数仿真实验

2.1 仿真实验过程

利用渐开线函数，生成渐开线样板的测量数据(xi,yi)，该数据是在理论的渐开线上叠加齿廓偏差Ei和坐标系建立误差X=(A,B,ψ)为

(7)

渐开线样板基圆半径rb的取值，样板精度级别2级对应的齿廓形状偏差最大允许值P的取值，以及展开角λi的终点λn的取值[13]，见表1。

表1 标准样板参数

为避免改变理想的渐开线参数值，造成无法将求解得到的最优渐开线参数Xk和理想渐开线参数X进行对比，二者之差ΔX=|Xk-X|，齿廓偏差Ei选择加入多个周期的余弦函数值，如式(8)，在此区间内等间距取n=10 000个值，即数据采样个数n=10 000。

(8)

为避免样板有些坐标点可能因基圆圆心坐标(A,B)的初值位于基圆内，造成渐开线参数无实数解，取展开角λi的起点λ1=5.0°，在此区间内等展开角取采样个数n=10 000。

若不存在坐标系建立误差，即渐开线参数A=0.0000 mm、B=0.0000 mm、ψ=0.0″，以样板3为例，可得在所测样板区间内的齿廓偏差Ei，如图2所示。

图2 不存在坐标系建立误差的仿真评定结果

从图2可看出，齿廓总偏差Fα=2.0 μm、齿廓倾斜偏差fHα=0.0 μm、齿廓形状偏差ffα=2.0 μm，该偏差与叠加齿廓偏差Ei一致。

加入坐标系建立误差，取渐开线参数A=0.100 0 mm、B=0.100 0 mm、ψ=100.0″。

根据式(7)生成渐开线样板坐标(xi,yi)，对此样板坐标(xi,yi)进行渐开线参数的求解。

2.2 坐标系建立误差对测量结果的影响

取渐开线参数的初值A0=0.000 0 mm、B0=0.000 0 mm、ψ0=0.0″。选择样板3生成的样板坐标(xi,yi)，不进行渐开线参数的求解，直接用渐开线参数初值评定渐开线样板，可得在所测样板区间内的齿廓偏差Ei，如图3所示。

图3 仿真数据的直接评定结果

从图3可看出，齿廓总偏差Fα=68.5 μm、齿廓倾斜偏差fHα=-68.7 μm、齿廓形状偏差ffα=4.0 μm，该偏远远大于图2给定的齿廓偏差，说明存在坐标系建立误差。下面将说明根据渐开线样板的测量数据，求出坐标系建立误差的过程。

2.3 模型的求解算法对比

将基圆圆心坐标(A,B)和起始角ψ作为未知参数直接求解时，系数矩阵M是3阶矩阵，迭代终止条件是3个渐开线参数在亚微米级不变。可得不同渐开线样板的渐开线参数求解结果见表2。

表2 直接求解结果

从表2可得出，max(cond(M)∞)=1.4×1010，直接求解的条件数很大，求解结果max(ΔA)=0.001 1 mm，max(ΔB)=0.004 3 mm，max(rb·Δψ)=0.004 5 mm，与理想的渐开线参数相差很大。说明直接求解算法的求解误差比较大。

表3(a)是样板1的求解结果，最优渐开线参数Ak=0.100 0 mm、Bk=0.100 0 mm、ψk=100.0″；表3(b)是样板2的求解结果，最优渐开线参数Ak=0.100 0 mm、Bk=0.100 0 mm、ψk=100.0″表3(c)是样板3的求解结果，最优渐开线参数Ak=0.100 0 mm、Bk=0.100 0 mm、ψk=100.0″；表3(d)是样板4的求解结果，最优渐开线参数Ak=0.100 0 mm、Bk=0.100 0 mm、ψk=100.0″。

可得max(cond(M)∞)=167.3，优化求解的条件数相较于直接求解的条件数减小，求解结果max(ΔA)=0.000 0 mm，max(ΔB)=0.000 0 mm，max(rb·Δψ)=0.000 0 mm，上述4种不同规格渐开线样板数据对应渐开线参数的求解精度均为亚微米级。说明优化求解算法的求解误差非常小。

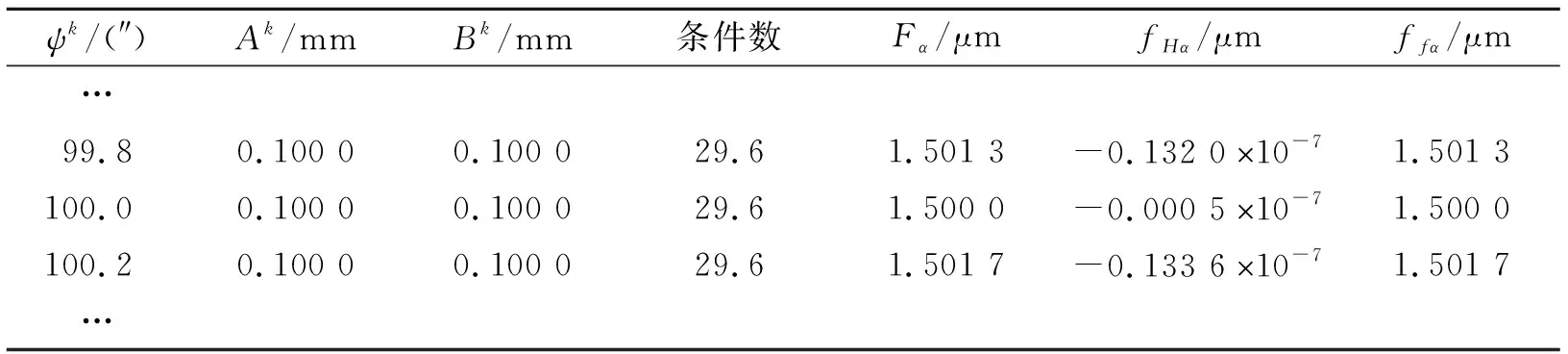
表3 优化求解结果

(b)样板2

(c)样板3

(d)样板4

2.4 仿真实验的坐标系校准

以样板3为例，取表3(c)中渐开线参数求解结果，修正测量坐标系，评定渐开线样板，可得齿廓总偏差Fα=2.0 μm、齿廓倾斜偏差fHα=0.0 μm、齿廓形状偏差ffα=2.0 μm，该偏差与图2给定的齿廓偏差一致。证明优化求解算法的正确性，采用校准后的测量坐标系，可获得准确的齿廓测量结果。

3 渐开线参数实测实验

3.1 实测实验过程

利用非相干线结构光法，测量渐开线样板的数据(xi,yi)。被测渐开线样板，如图4所示。

图4 被测渐开线样板

此渐开线样板的参数见表4。

表4 实测样板参数

非相干线结构光法测量系统主要包括：非相干光源、汇聚光路、装夹装置和图像采集系统四部分，如图5所示。

图5 非相干线结构光测量系统

其中非相干光源由LED光源和狭缝装置组成，用于产生非相干线结构光。汇聚光路由透镜组组成，主要实现光条宽度的调节。装夹装置由装夹机构、水平位移台、旋转位移台和俯仰台组成，主要实现工件的装夹、移动、旋转和微调。图像采集系统由相机、镜头和移动台组成，相机选用510万像素CCD相机，镜头选用畸变系数小的双远心镜头，移动台可以控制图像采集系统沿水平和垂直方向移动。此测量系统的轮廓测量精度约为4 μm，横向测量范围最大为10 mm，工作距离为63 mm，景深为1 mm。

实验原理是非相干光源发出的球面光经狭缝变为线结构光，通过汇聚光路变细后的线结构光照射在被测工件表面上，经被测表面反射后成像于CCD的光敏接受元件上，通过测得的像点位移信息，计算出被测工件表面的轮廓信息。

由于被测渐开线样板的齿廓长度大于非相干线结构光法的横向测量范围，实验只选取其中一段齿廓进行测量。测得渐开线样板坐标(xi,yi)，对此样板坐标(xi,yi)进行渐开线参数的求解。

3.2 渐开线参数初值的选取

该实验仅测得有限视野下的渐开线样板坐标(xi,yi)，数据采样个数n=1 621，未测得被测齿轮回转中心坐标。提出通过移动和旋转样板坐标(xi,yi)，将其与理论渐开线对比，使渐开线参数的初值为A0=0.000 0 mm、B0=0.000 0 mm、ψ0=0.0″。具体步骤如下：

① 渐开线样板数据首尾两点的连线，记为线段CD；样板数据跟随线段CD旋转，旋转至线段CD与X轴平行，绘制样板数据构成的曲线；

② 样板数据中与线段CD距离最远的数据点，记作点E；过点E作射线EF，射线EF与X轴的夹角为τ1=tan(α)，α是被测样板分度圆压力角，点F在靠近基圆圆心方向取值；过点E作圆S，圆S的半径为r1=r，r是被测样板分度圆半径；得到射线EF和圆S的交点位置O；

③ 以点O作为基圆圆心，-τ1作为渐开线起始角，绘制基圆G和理想渐开线；

④ 利用观察法，通过调整射线EF与X轴夹角τi和圆S的半径ri，重复步骤②和步骤③，使理想渐开线与被测样板曲线相重叠，记录此时的基圆圆心O的坐标(a,b)和渐开线起始角-τ的角度；

⑤ 将相重叠时的基圆圆心O在X轴方向上移动-a，在Y轴方向上移动-b，坐标轴逆时针方向旋转τ。

可得初步建立的测量坐标系，如图6所示，粗线为被测渐开线样板数据构成的曲线，细线为理想的渐开线。

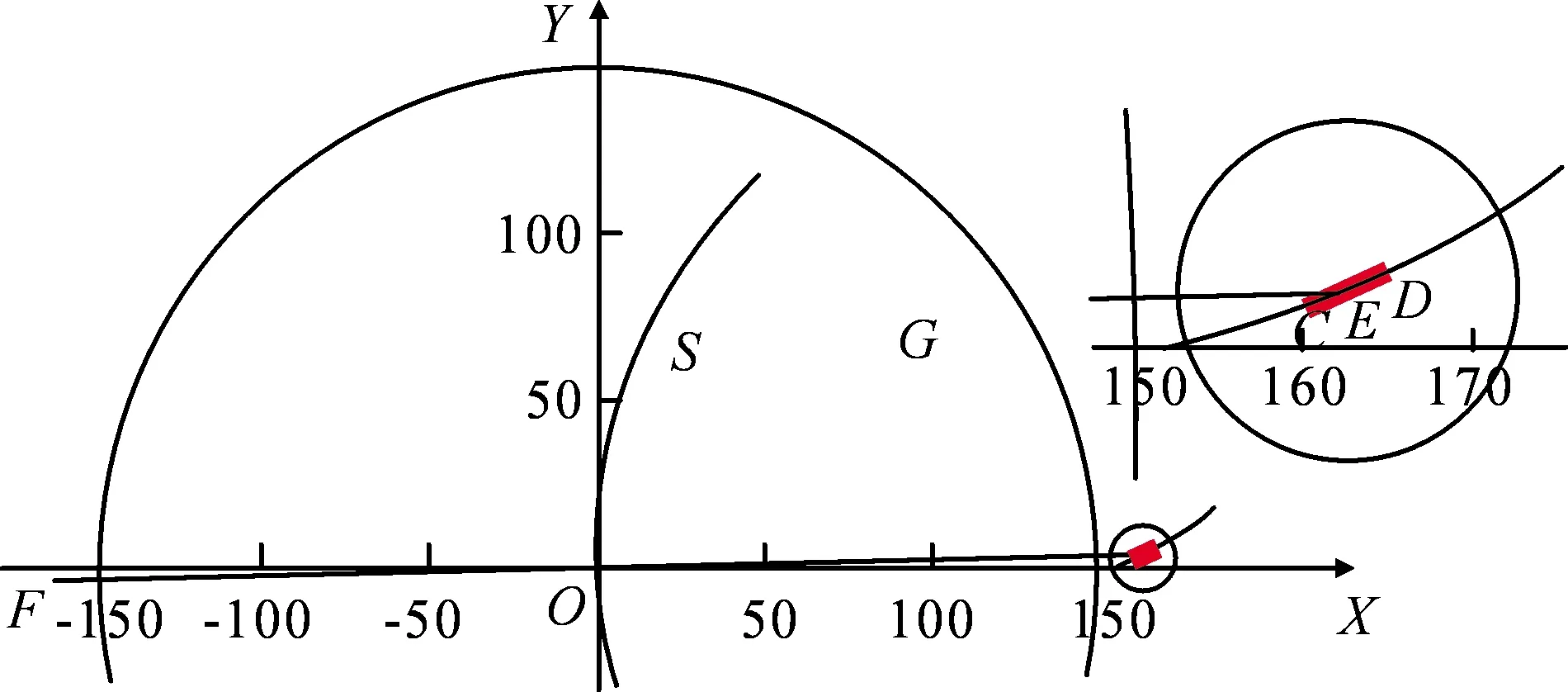
图6 测量坐标系的初步建立

3.3 渐开线参数的优化求解

当将起始角ψ作为已知参数优化求解，迭代终止条件和搜索终止条件与迭代终止条件为3个渐开线参数在亚微米不变，搜索终止条件为ΔAk<5×10-4mm且ΔBk<5×10-4mm一致。

第1次求解，起始角ψ的取值范围是[-20 000.0″,20 000.0″]，取值间距是2 000.0″；第2次求解，取值范围是[-4 000.0″,0.0″]，取值间距是200.0″；第3次求解，取值范围是[-1 200.0″,-800.0″]，取值间距是20.0″；第4次求解，取值范围是[-1 020.0″,-980.0″]，取值间距是2.0″；第5次求解，取值范围是[-1 002.0″,-998.0″]，取值间距是0.2″。可得渐开线参数求解的结果见表5。从表5可得出，求解得到的最优渐开线参数Ak=-0.502 9 mm，Bk=0.362 2 mm，ψk=-998.8″。

表5 实测数据的渐开线参数求解结果

3.4 实测实验的坐标系校准

取表5中渐开线参数求解结果，修正测量坐标系，评定渐开线样板，可得在所测样板区间内的齿廓偏差Ei，如图7所示，所测样板展开角λi的起点λ1=21.6°，终点λn=26.7°。

图7 实测数据的校准评定结果

从图7可得出，齿廓总偏差Fα=4.7 μm、齿廓倾斜偏差fHα=0.0 μm、齿廓形状偏差ffα=4.7 μm，该偏差与此系统的轮廓测量精度一致。证明优化求解算法的实用性，可获得准确的齿廓测量结果。

4 结 论

1) 测量坐标系存在误差的情况下，构建求解渐开线样板基圆圆心坐标和渐开线起始角的模型，提出用渐开线样板校准测量坐标系的方法。

2) 采用仿真方式生成的4种不同规格渐开线样板数据和采用非相干线结构光法测得的渐开线样板数据，通过2阶矩阵和1维优化算法，求解构建的渐开线参数模型，以齿廓总偏差最小为优化目标，求出渐开线参数，可获得亚微米级的坐标系建立精度和准确的齿廓测量结果。

3) 一般校准齿轮测量设备的渐开线样板基圆半径与被测齿轮的基圆半径大小一致，用于校准测量设备的渐开线样板一般带有回转轴线，而大尺寸的高精度渐开线样板制造难度比较大，本文建议研制一种用于大齿轮测量设备校准无回转轴线的小型渐开线样板。