基于改进时间序列DEA的石油企业技术创新效率评价

杨智勇余晓钟白 龙，2钟书丽

（1.西南石油大学经济管理学院，四川 成都 610500；2.中国石油西南油气田公司，四川 成都 610213；3.长城战略咨询公司，四川 成都 610000）

0 引言

数据包络分析（Data Envelopment Analysis，简称DEA）自1978年提出发展至今，已经受到众多学者青睐，DEA广泛应用于各个领域相对有效性评价。目前国内外文献主要集中于国家、地区、行业具有多个相同性质决策单元的相对效率评价，而针对单个决策单元的评价较少，特别是以不同时间段作为决策单元的有效性评价就更少［1］。究其原因，首先，DEA方法要求决策单元为一组截面数据或一组面板数据，如果不能获取面板数据或面板数据不适用，那么也不能使用指定某时间点的样本值作为截面数据来计算效率值。其次，决策单元的一组单期截面数据，仅能评价在某个指定时间点的技术创新效率，不能反映时间序列上特定研究对象的效率演进过程［2］。Malmquist指数虽能计算出技术进步效率，但对面板数据的数量有要求且不能反映单个企业每个时间点上的技术进步效率。目前，针对某个或少数几个样本评价时，有部分学者直接将时间作为决策单元计算效率值，未考虑不同时间点的外部环境因素对技术进步影响，即不同时间节点技术水平的差异性。

石油企业技术创新效率评价指标体系的构建要考虑石油企业的特殊性，需将其特点融入评价体系，指标选择过程中要兼顾数量恰当、分层明确，指标设计时要考虑数据收集的难易程度及完整性［3］。我国油气产业发展至今，由于各种因素我国石油资源和市场形成了中国石油天然气集团公司（以下简称中国石油）、中国石油化工集团公司（以下简称中国石化）、中国海油石油总公司（以下简称中国海油）为主的三大石油公司几乎占据了我国的石油资源和市场［4］。1978年以来，国有石油企业对人事、劳动、分配制度进行改革，三项制度实施多年虽有成效但推进艰难［5］。科学技术的进步使得大数据处理能与石油企业结合，通过历史数据能有效分析公司成本构成及成本费用变化趋势，为企业下一步降本增效提供决策依据［6］。为此，希望通过DEA模型的应用，能为我国三大石油公司解决技术创新模块上的历史问题提供一些思路。DEA模型的应用对样本和变量选取是很严格的［7］，三大石油企业市场结构、经营业务、集团规模也较为相似，评价其技术创新效率时，更具有可比性。笔者研究发现现行的DEA基本模型不适用该评价，C.Lynde和J.Richmond（1999）构建的时间序列DEA模型适用但存在一些问题，故在此基础上对时间序列DEA模型进行了改进。

1 模型建立

1.1 时间序列DEA模型

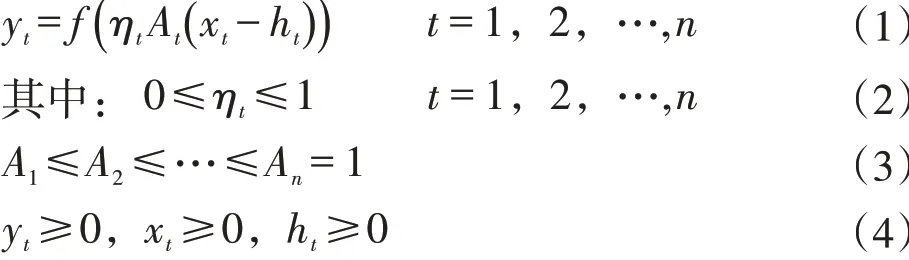
式中，yt∈Rm表示在t时刻的产出值，xt∈Rn表示在t时刻的投入值，ht∈Rm表示投入要素的松弛变量，At∈Rm表示技术进步指数，ηt∈Rn表示所有投入利用的总体技术效率。

式（3）表示技术是不可逆的，技术进步是与知识积累相关的。由上述公式推理并简化我们的假设f函数，令其为一阶齐次线性函数，即为任意常数，忽略生产边际递减的影响，并假设投入值x1t的生产技术是多变的，而其他因素固定不变，建立以投入导向的效率函数图，如图1所示。

如图1所示，X轴表示投入输入，Y轴表示投入输出。当ht＝0时，表示函数无松弛变量；当ηt＝1时，表示如果资源利用有效，那么给定的技术条件是适用的。如果ht＝0并且ηt＝1同时成立，则函数是一个没有考虑生产利用无效的标准生产函数。如果不存在松弛变量以及投入资源被有效的利用，则标准化At＝1得到函数那么此时f函数为最佳生产前沿面。

以投入指标1为例，在时间t＜n，P点表示实际输入和输出的结合表示投入导向下技术非效率的程度；如果因素明确松弛变量存在ht≠0，RQ就表示在此条件下的技术非效率，即松弛变量对yt的影响。因为存在着技术不可逆At＝An，SR则表示由于At≤1，有效投入是进一步按比例缩小的。因此我们定义在时间点t上的实际投入向量xt，若产出水平是yt情况下其有效投入向量zt：

根据DEA基本原理估计f函数以及参数ηt，ht和At。令e为一个n×1的向量，θt是一个标量其函数表示为

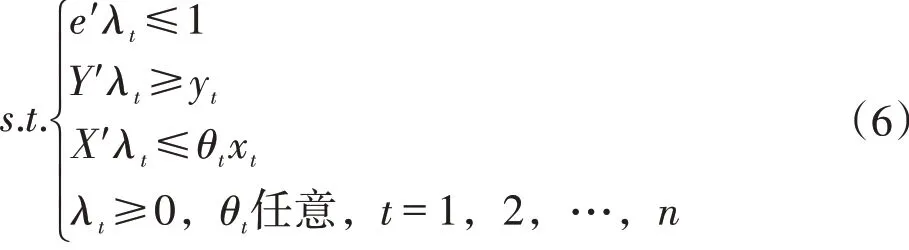
式中，X′表示决策单元DMUj的投入指标集合，其中m表示投入指标的个数［8-9］，Y′表示决策单元DMUj的产出指标集合［10］，s表示产出指标的个数，λt表示第t个决策单元DMUt的组合权重［11］。

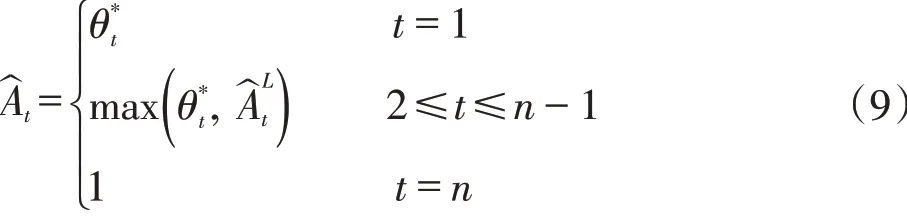
式中，γjt是第j个要素投入利用的相对强度，即RQ的距离，φjt表示总体技术效率与第j个投入利用的相对强度的乘积，即RP的距离，由于对估值的过程中将技术进步指数考虑其中，满足构建的生产前沿函数即SP距离能够被求出来，即由公式（7）可以进一步估计φjt：

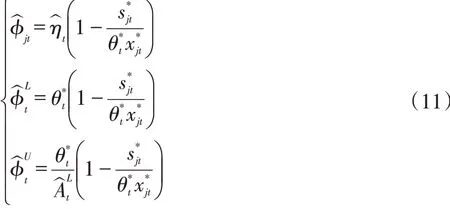
1.2 模型改进

原有模型偏向理论化，并未清晰表述估值的计算方式，通过模型改进使得在应用过程中简单有效，结果准确可靠。王兵等人在计算我国1952-2000年的生产率与效率时也利用了这个模型，其方法是利用超效率DEA模型找出最大综合效率值，然后运用C2R-DEA的模型求出的效率值去除最大综合效率值得出如果使用原式（6）计算出来的综合技术效率值达到DEA有效时均为1，达到DEA有效，而当大多数的决策单元值为1时，不能满足进一步模型计算要求，故利用Andersen和Petersen（1993）提出的超效率DEA（SE-DEA）模型［14］替换式（6），这个模型打破原有时间序列DEA一个投入多个产出的局限，使得实际应用中能够适用于多投入和多产出的相对有效性评价：

在计算超效率DEA过程中，为了避免计算过程中模型数量级差异巨大导致运算失败，将数据标准化。经多组数据实验佐证，投入产出的数据标准化后与标准化前所计算的SE-DEA的结果差异极小，可忽略不计。时间序列DEA的思想仍然是最小的投入与最大产出之间的相对关系，因此选择不改变向量极性的标准化处理公式：

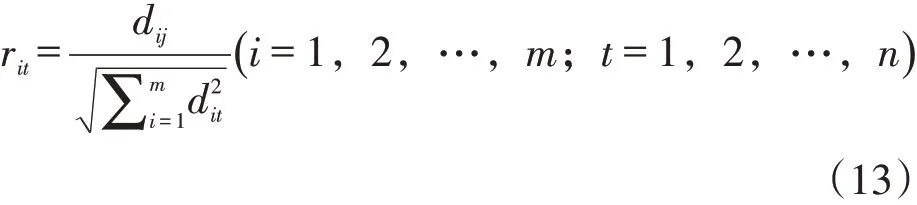
式中，rit表示向量标准化处理结果值，dij表示各指标不同年份的值，t表示时间年份，i表示各个指标。为了满足的取值范围要求，对求出的超效率DEA的综合效率值标准化处理得到新的直接运用超效率DEA求出的综合效率值去除最大综合效率值，更符合计算过程的一致性，即：

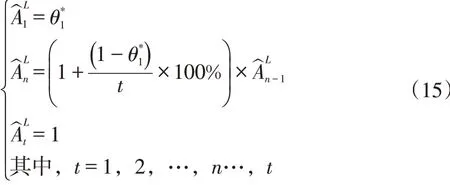
2 模型应用

2.1 评价样本的选择以及指标的确定

石油企业技术创新重点研究领域包括：勘探开发技术，石油化工技术，安全、环保、节能等技术。结合国内外研究成果，建立石油企业技术创新效率评价指标，如表1所示。指标通过收集三大石油企业2006-2016年的年报统计数据。

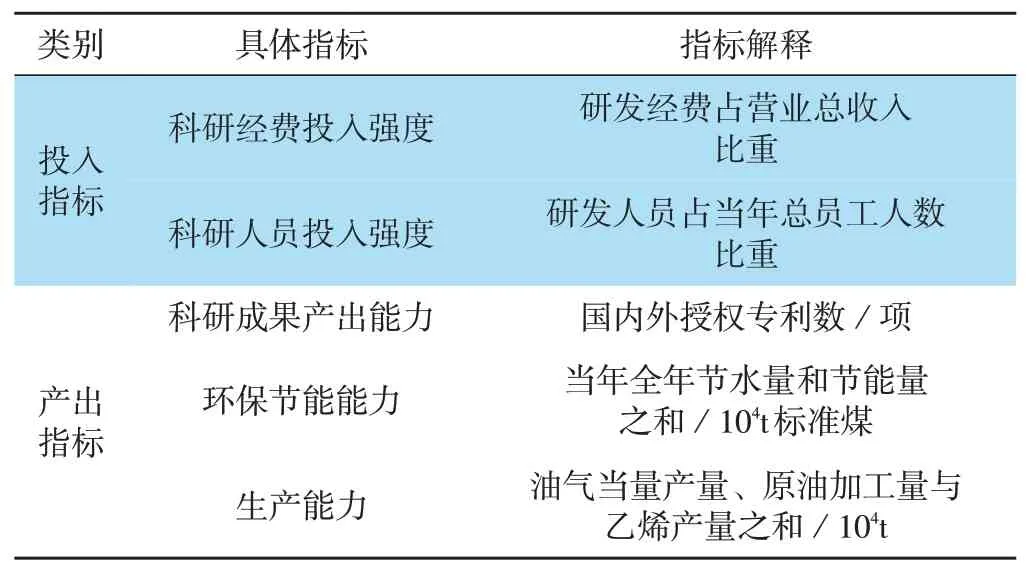
表1 石油企业技术创新效率评价指标

2.2 应用及结果分析

根据时间序列DEA模型及改进方法分别求出三大石油公司技术创新效率各参数值，如表2所示。

在不考虑时间因素带来的技术进步条件下的SEDEA综合效率值来看，中国石油技术创新的综合效率均值是1.042 0；中国石化技术创新的综合效率均值是1.043 8；中国海油技术创新的综合效率均值是0.928 3。由松弛变量来看，总体上三家石油企业的投入要素松弛范围很小，科研人员比科研经费的投入强度略低了一点。从技术进步指数来看，各企业技术创新效率的起点不同影响了技术进步效率，中国石油最高，其次是中国石化，最后是中国海油。

将时间因素考虑其中的科研经费投入和科研人员投入的相对利用强度φ1t和φ2t可以看出，中石油的科研经费投入效率下边界值和上边界值的均值范围在0.818 3～0.904 5，科研人员投入效率下边界值和上边界值的均值范围在0.803 2～0.889 5，总体的变化也很平稳，上、下边界值差距较小。中国石化的科研经费的投入效率上、下边界均值的范围在0.686 8～0.768 6，科研人员投入效率的平均范围在0.733 3～0.824 7，总体变化幅度和上、下边界估值差距较小。中海油的科研经费的投入效率上、下边界均值的范围在0.526 3～0.695 6，科研人员投入效率上、下边界均值的范围在0.385 6～0.479 5，两个投入变量的效率值变化幅度都非常大，且变化趋势不具有一致性。

2.3 结果比较

DEA基本模型有一定的局限性，无法动态的反映各投入指标的生产效率，也不能对单个企业进行评价。改进前的时间序列DEA模型由于忽视了样本的数量限制，得出的技术进步值无法满足模型计算要求，导致结果与实际不一致。改进后的时间序列DEA模型满足了计算过程的一致性，并且满足生产函数计算的约束条件。通过改进后的时间序列DEA模型对我国三大石油公司技术创新效率的分析，能够动态的反映出近些年我国三大石油公司技术创新效率变化的趋势、不同时间阶段的技术创新效率值以及投入要素利用的效率。研究结果表明我国三大石油公司的技术创新效率处于一个中等水平，与实际情况相符。同时印证了庞大的企业规模、雄厚的经济实力、强大的人才号召力以及国家政策的导向，更有利于企业技术创新。

3 结论与展望

总体而言，时间序列DEA模型解决了将时间序列作为决策单元的问题，并且很好地利用了时间序列的动态变化优势。同时时间序列DEA的生产函数模型较DEA基本模型能够进一步分析各投入指标的利用相对强度，也能够分析各产出指标的产出相对强度，对于深入研究企业各投入产出值实际情况及针对性提出应对措施具有良好的实践意义。模型的改进使得时间序列DEA模型在实际应用中更有逻辑性、可操作性和准确性。相比于改进前具有一定的优势，还能够深入分析各决策单元之间的差异，但对于投入利用效率情况仅仅给出了一个范围，缺乏一个准确的值。在多产出和多投入指标情况下，进一步研究并区分投入和产出的效率值，并结合其他模型对其优化的问题值得未来研究。