基于指数与倍数修正系数的天然气产量预测方法优化
陈艳茹余 果邹源红方一竹郑 姝
(1.中国石油西南油气田公司勘探开发研究院,610041;2.中国石油西南油气田公司,610051)
0 引言
随着国民经济的增长及生产力的提高,油气资源的需求量日益增加,油气供需矛盾已成为影响我国经济社会发展的重要因素。深入研究油气储产量变化规律并以此为依据建立预测模型,能够科学预测我国未来油气发展趋势,对国家制定能源开采计划及调整发展战略具有重要意义[1]。油气田产量大小受许多因素的影响,但从油气开发全过程看,一般都要经过产量上升、产量相对稳定、产量下降直至枯竭等几个阶段,具有典型的生命旋回特征,这是用峰值模型对油气田开发全过程进行描述的客观基础。对具体的气区或气田(气藏)产量趋势进行预测时,选择的峰值模型是否适宜,应以具体的实际分析为依据。由于各类峰值模型均有其适用条件与局限性,在峰值模型不能有效拟合具体气区或气田(气藏)产量发展特点时,需要对其进行优化与改进,并通过预测、检验,判断其合理性,检验后的峰值模型才能适用于该区域的产量预测。
1 油气产量预测模型
1.1 翁氏预测模型
对于油气田资源开采体系,开采全周期过程可以用翁氏模型表述[2]:

式中,Q为油气田产量,104t/a(油田)或108m3/a;t为翁氏时间,a;y为油气田某一生产年份,单位a;y0为油气田生产参考起始年份,a;n、A、C均为模型常数[3-4]。
将式(2)代入式(1)得到新的产量计算公式:

由于y-y0实际代表油气田的实际生产时间,可采用油藏标准符号t代替,令t=y-y0,B=AC-n,a=1C,那么式(3)可简化为:
可采储量为油气开采全生命周期内的产量加和,推导NR公式如下

将式(4)代入式(5)可得:
令x=at,式(6)可转换为

式中,Γ(n)+1为完全伽马函数,可通过查询伽马函数表获得。
相应的剩余可采储量公式如下

在计算可采储量NR时,首先需要确定模型常数a、B,本文通过一种线性试差的方法进行求解。将式(4)两边取对数得到
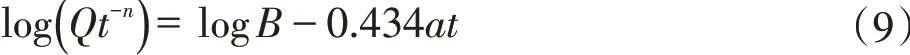
假设α=logB,β=-0.434 3a,可得线性试差方程如下:

通过采用不同的n值进行检验计算,选取使公式两端线性相关性最好的n值作为计算指数,从而计算出模型常数a和B,再将模型常数代入产量与可采储量式中计算,就可实现全生命周期产量预测。
1.2 Weibull预测模型
Weibull模型不但可以全周期预测油气田产量,还可以预测油气田的可采储量、最高年产量及发生时间。其产量计算公式如下[5-7]:

为确定最高年产量的发生时间,由上式对时间t进行求导:
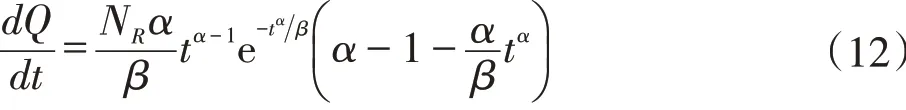
当dQ dt=0,可得到最高产量的发生时间tm为:

为确定可采储量NR和产量Q的数值,需确定模型参数α和β,将式(11)改写为:

上式两端取对数得:
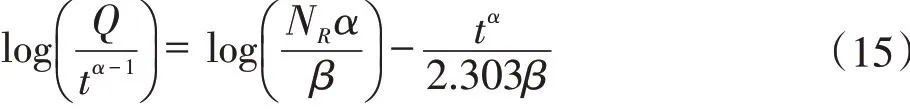
假如令
式(15)可以改写为:

若给予不同的指数α值,开展试差法求取等号两端线性相关性最高的α值[8-10],利用该数值进行线性拟合,得到线性回归方程的截距a和-b斜率的数值,并求出可采储量NR及模型参数β。同理,将确定的模型参数代入产量式中,可实现全生命周期产量,最高年产量及发生时间的预测。

1.3 基于指数与倍数修正系数修正的产量预测模型
根据翁氏和Weibull两种模型的产量计算公式(4)及式(11)可以看出,其预测结果受时间t的指数n和α的影响较大,指数的精准计算需要高精度地一次拟合Q与t的衍生式,指数的计算误差容易造成产量预测结果出现指数倍的偏差[11-12]。因此,为纠正计算误差,建立了一种指数及倍数修正因子方法,修正原理是分别在翁氏预测模型式(4)和Weibull预测模型式(11)中加入倍数修正系数和为指数修正系数,修正后的产量计算公式如式(19)及式(20):
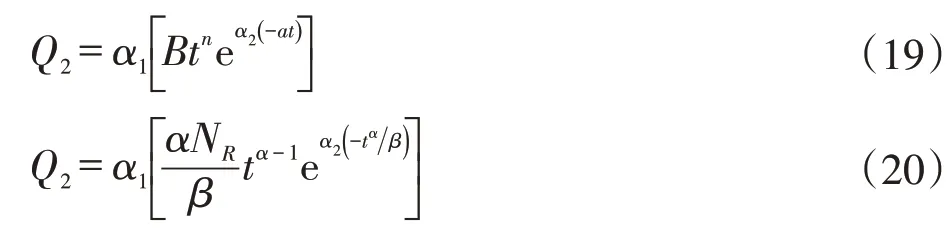
式中,Q2为修正后的产量值,单位104t/a(油田)或108m3/a;α1为倍数修正系数,无量纲;α2为指数修正系数,无量纲。
在产量Q的计算公式中,由于e指数函数的变化速度相对于t指数函数更快,因此在e指数中添加指数修正系数α2后,可以使预测曲线更接近原始曲线,同时通过α1修正整体倍数关系,可以进一步减小误差。修正系数的计算原理如下:
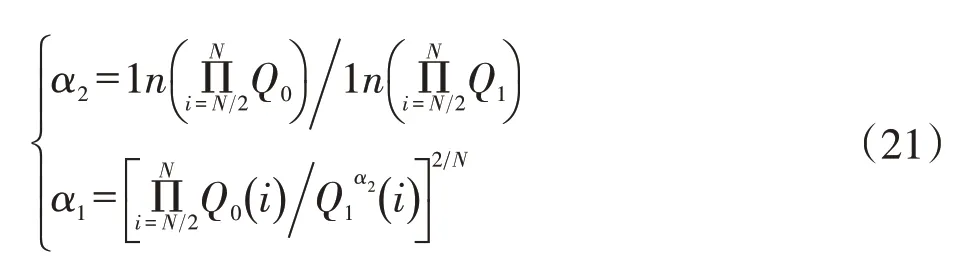
式中,Q0为原始产量值,单位104t/a(油田)或108m3/a;N为Q0序列包含的元素个数。
由于原始数值曲线随着时间推移很难一直保持稳定的函数关系,因此推荐选取原始数据的后半段作为参照修正值,对整体数值修正。
产量Q的t子函数的指数n与α影响产量的数值大小与曲线形状,指数与倍数系数仅能减小Q的数值计算误差,不能修正Q的变化规律。因此,在修正计算后,在原指数n与α附近重新选取多个指数的数值再次计算,与原始数值Q0进行相关性分析,选取使公式两端线性相关性最好的指数值作为计算指数。基于指数与倍数修正系数进行改进的预测模型可以减少修正预测模型与原始数据变化规律的误差,提高拟合精度,使预测结果更加可靠。
2 应用举例
四川盆地为典型的大型复杂叠合盆地,历经60余年的勘探开发,主要经历三个阶段:1953-1977年的探索起步阶段,1978-2004年的稳步增长,2005年至今的发展壮大阶段。伴随勘探开发节奏,盆地的天然气产量发展也出现了三个明显的峰谷起伏,整体上仍呈现持续增长的态势,如图1所示。考虑年产气量整体呈上升趋势,伴随较小的局部峰,局部波动处的数值突变较小,对整体类指数增长趋势影响较小,因此产量计算可采用翁氏和Weibull单峰值预测模型方法。
以四川盆地1953-2019年的天然气历史产量数据为基础,通过历史数据拟合,检验相关性合格后再预测分析至2140年产量变化趋势。将1953年作为原始时间点t=0,t=1时间点代表1954年,其他时间点依次类推。首先,采用传统翁氏预测方法的产量衍生式与时间进行拟合,由于产量Q的衍生式与时间t不完全呈线性关系,因此分别选取t=30~50及t=55~60两段线性特点较好的数值点进行阶段线性拟合(图2)。如图3所示,为产量的拟合结果与原始数值对比,可以看出两种拟合结果仅在相应时间段内精确度较高,整体上偏离了四川盆地实际的产量发展趋势,因此传统模型是不适用于四川盆地天然气产量预测的。
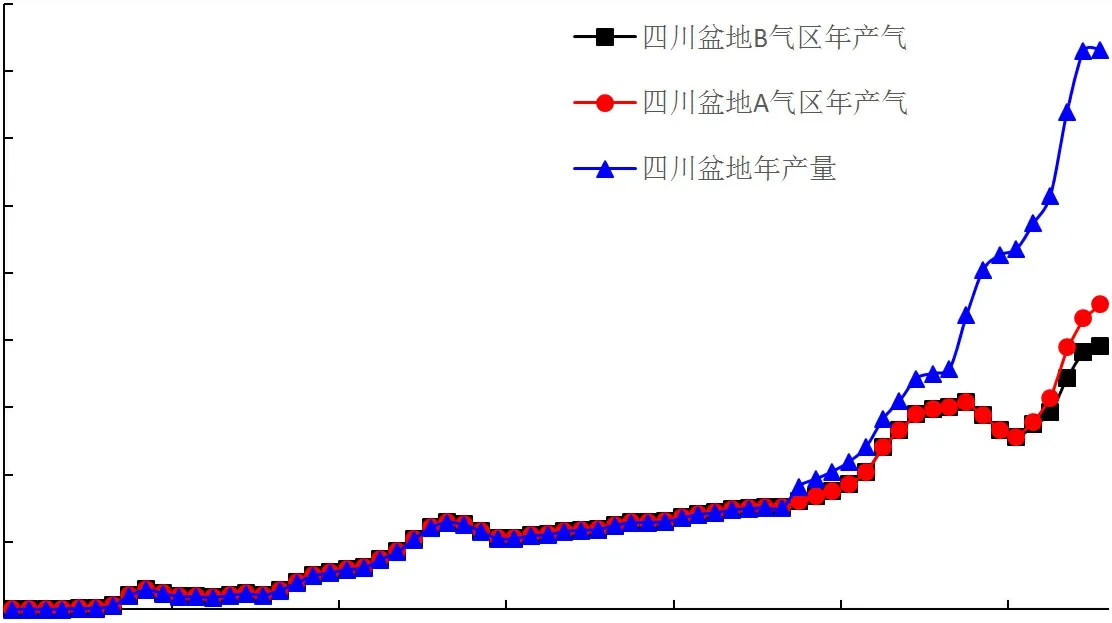
图1 四川盆地年产量原始数据图
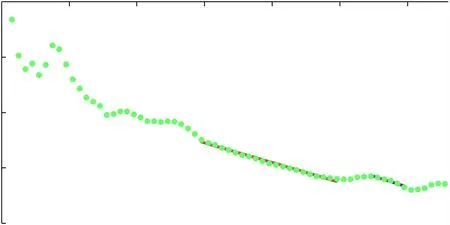
图2 产量衍生公式与时间的线性拟合
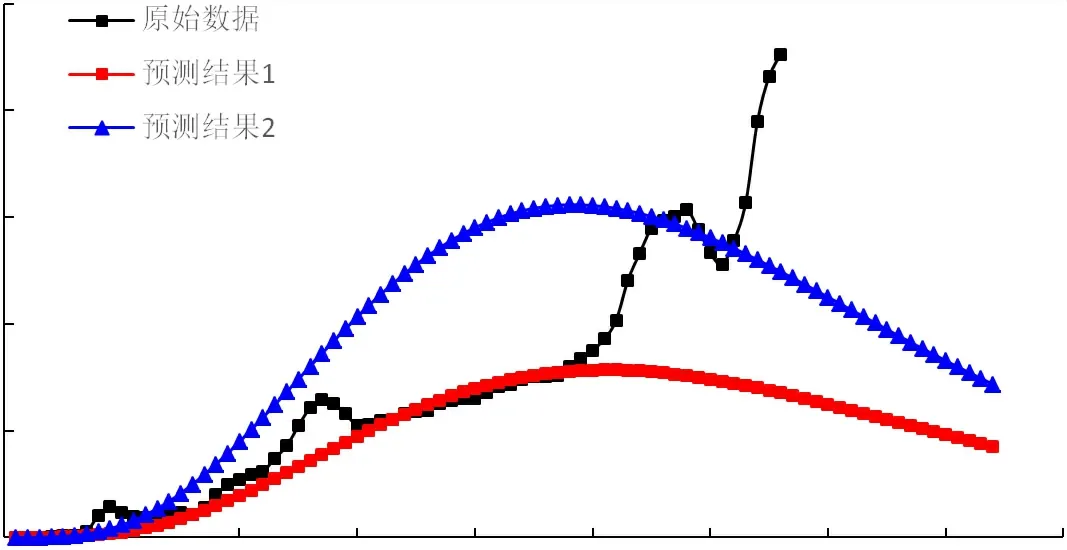
图3 产量线性拟合预测结果
采用指数与倍数修正系数改进的翁氏与Weibull模型,在整体线性拟合的基础上再进行系数修正校正拟合结果,改进后模型的预测曲线与四川盆地天然气历史产量曲线较为接近,拟合相关性高,可适用于四川盆地天然气产量预测。通过指数及倍数拟合修正后,再选取原始翁氏模型指数N及Weibull模型指数附近的值代入计算,可得到不同指数条件下的产量预测曲线,如图4~图9所示。
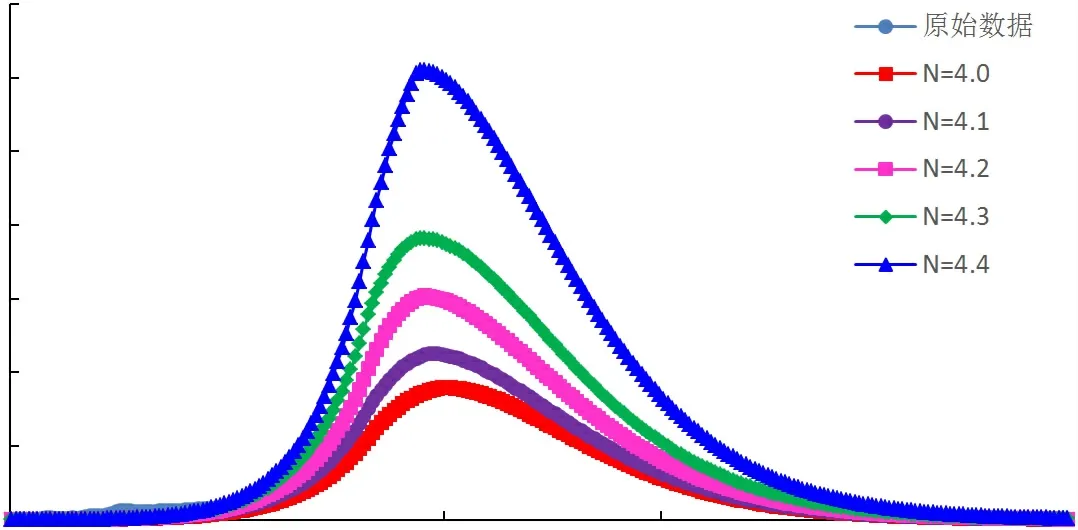
图4 翁氏模型四川盆地A气区年气产量预测结果
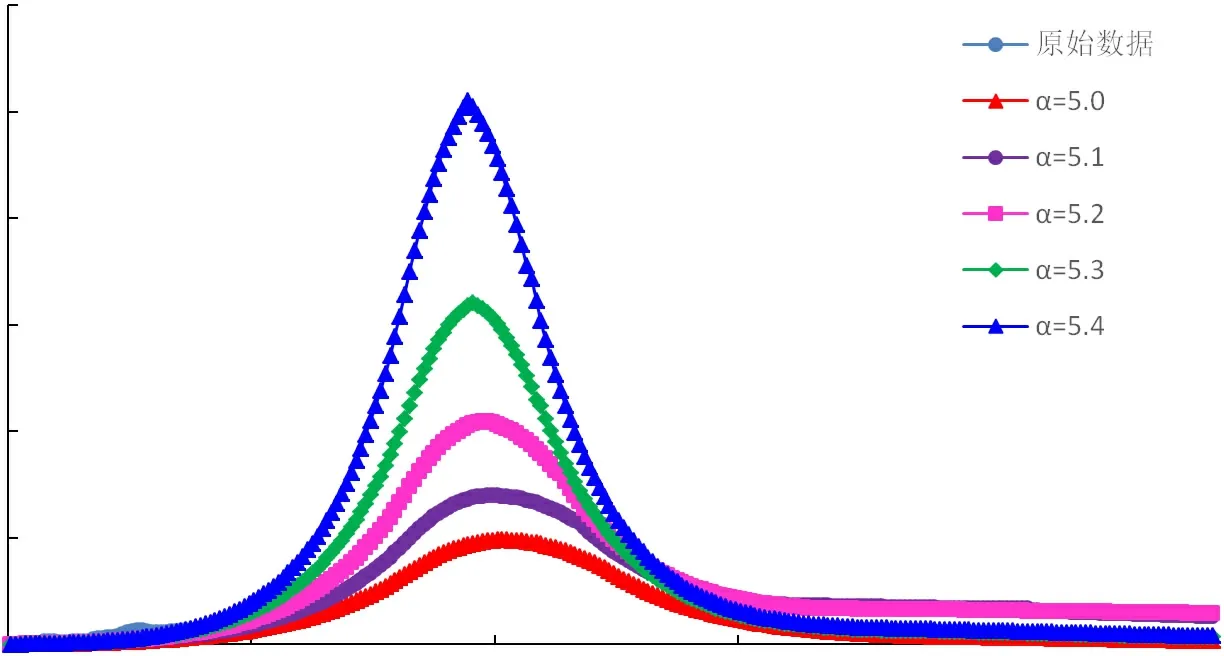
图5 Weibull模型四川盆地A气区年气产量预测图
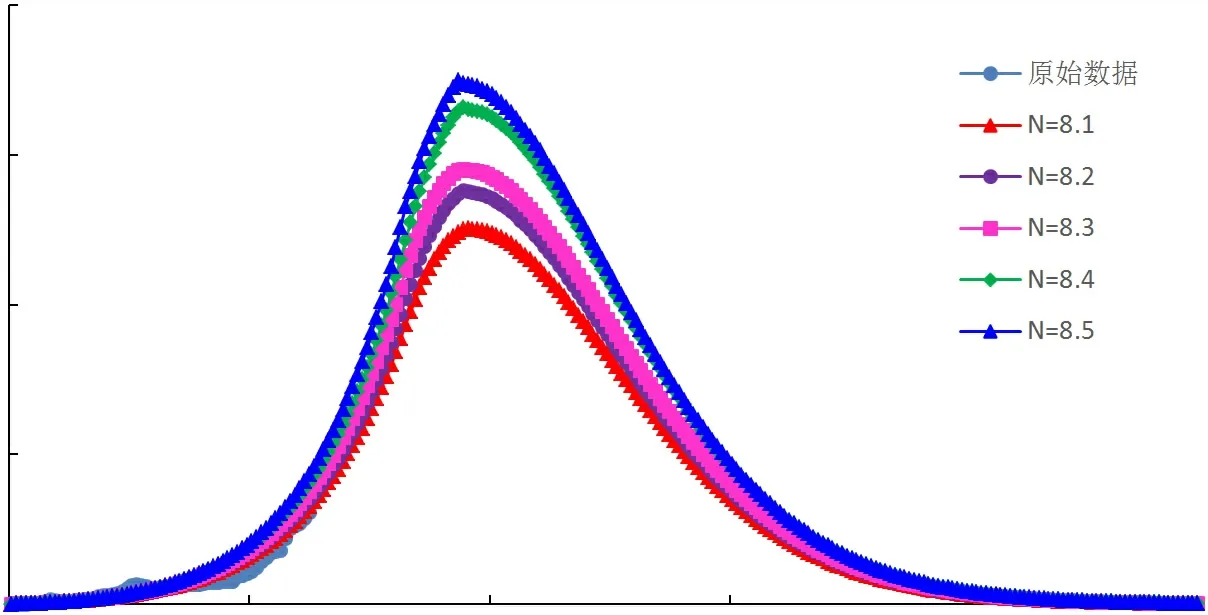
图6 翁氏模型四川盆地年气产量预测结果
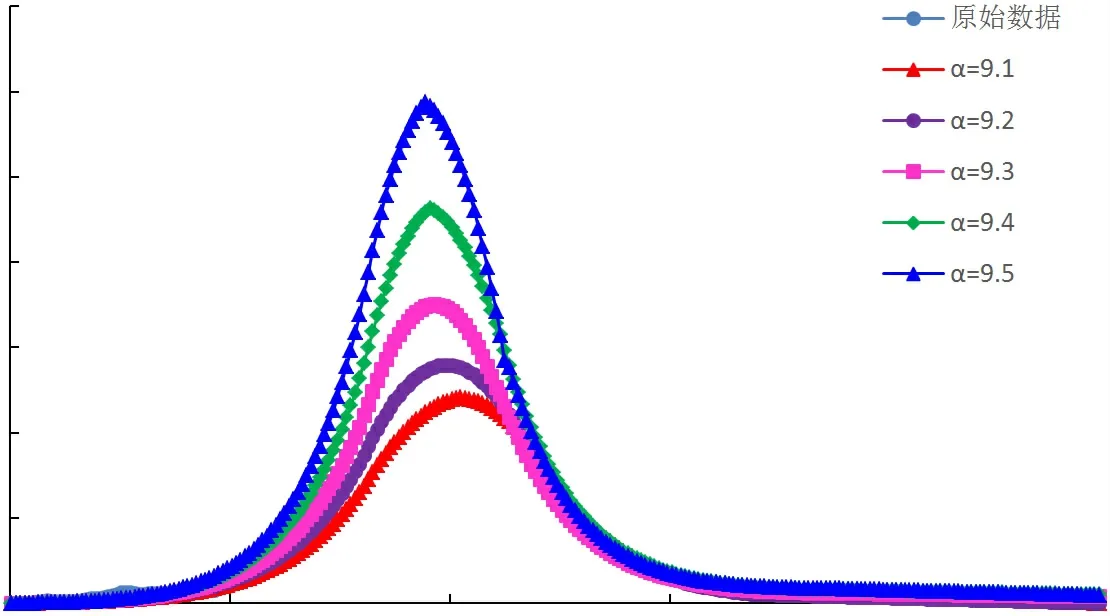
图7 Weibull模型四川盆地年气产量预测结果
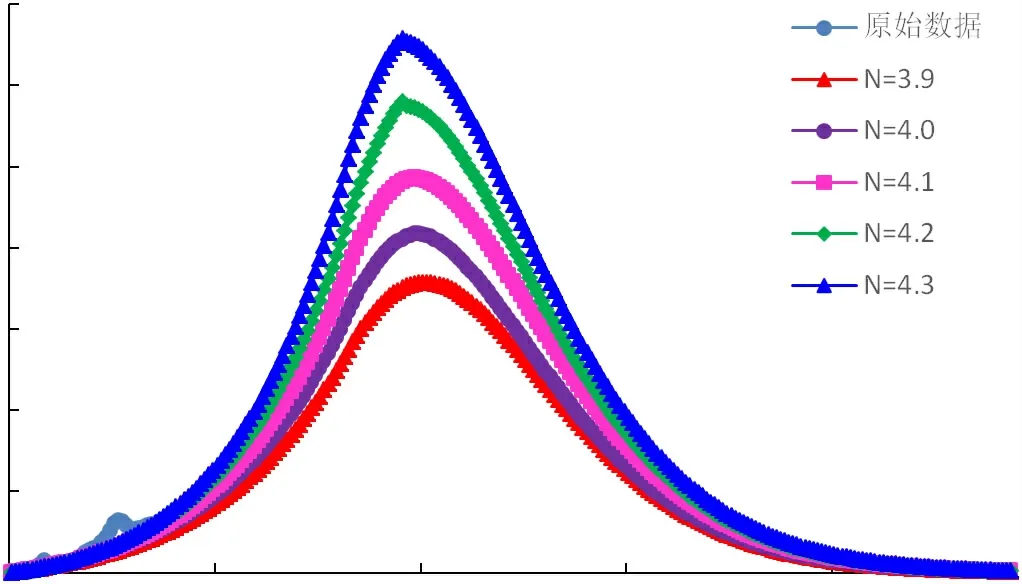
图8 翁氏模型四川盆地B气区年气产量预测结果
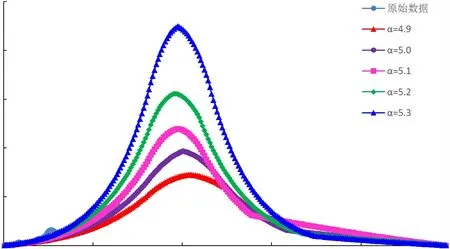
图9 Weibull模型四川盆地B气区年气产量预测结果
将不同产量预测曲线的计算结果与原始数据进行相关性分析,选取相关性最好的一组作为预测模型,最终预测模型的相关系数、最大产量及其发生时间如表1所示。总的来说,两种修正后模型的预测结果相接近:①改进翁氏模型预测四川盆地峰值产量时间出现在2047年,峰值产量为1 453.28×108m3;改进Weibull模型预测四川盆地峰值产量时间出现在2049年,峰值产量为1 750.38×108m3。②改进翁氏模型预测四川盆地A气区峰值产量时间出现在2050年,峰值产量为1 128.81×108m3;改进Weibull模型预测四川盆地A气区峰值产量时间出现在2050年,峰值产量为1 047.88×108m3。③改进翁氏模型预测四川盆地B气区峰值产量时间出现在2051年,峰值产量为486.46×108m3;改进Weibull模型预测四川盆地B气区峰值产量时间出现在2050年,峰值产量为478.40×108m3。
应用表明,基于指数与倍数修正系数修正的翁氏及Weibull预测模型能充分拟合四川盆地产量的整体发展趋势及历次产量突变,预测结果显示出四川盆地发展潜力巨大,未来20年左右将是其产量的快速发展期,对整体气区或气田(气藏)中长期发展战略的制定具有较好的指导作用。但天然气产量预测是一个复杂的过程,仅以数学原理为基础的预测模型不能完全考虑地质条件、开发技术政策等各环节的影响,实际应用中还需要结合气区或气田(气藏)的阶段发展形势进行综合考虑。
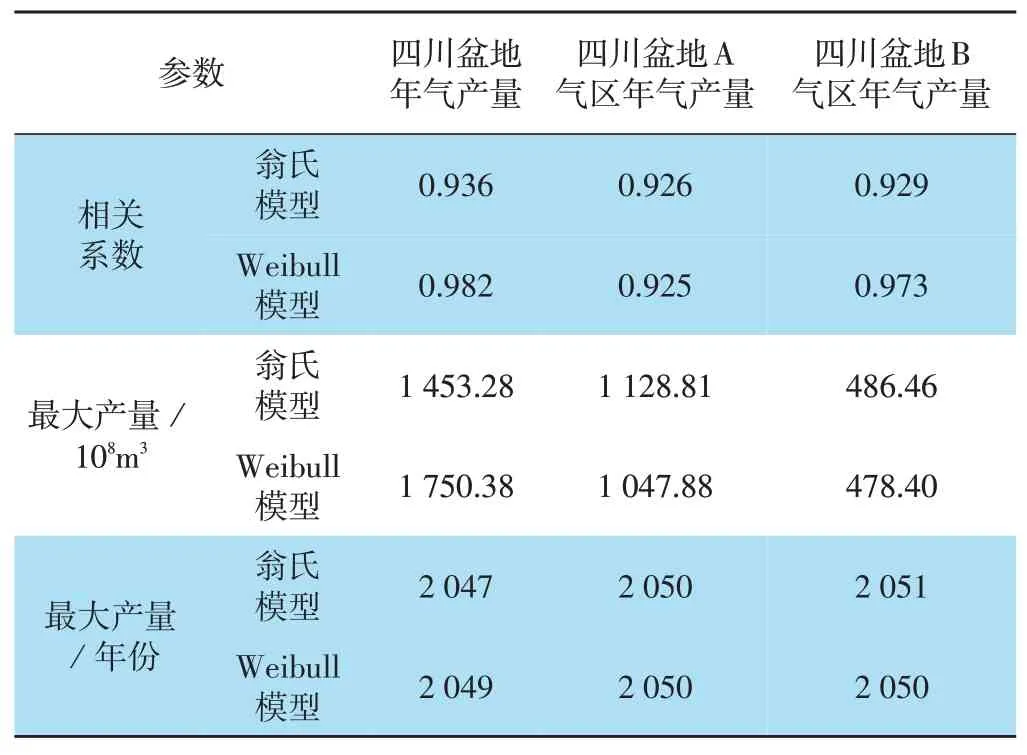
表1 四川盆地年产量数据统计
3 结论
1)传统的翁氏和Weibull产量预测模型受线性拟合计算影响较大,易造成指数倍的误差。使用双权重修正因子方法可以修正计算误差,基于原始数据建立的倍数修正系数α1和α2指数修正系数可以精准地校正计算结果。
2)在修正系数计算的基础上,利用t子函数指数多值求解产量,并与原始数据相关分析选取更优解。t指数修正法可以减少预测曲线与原始数据变化规律的差异性。
3)通过四川盆地预测模型的构建,发现基于上述方法改进的翁氏模型和Weibull模型均能够较准确盆地全生命周期的产量变化趋势,且两种算法得出的预测值接近,都具有较高的精准度。

