“子弹-木块”模型的高端备考策略剖析
谭程

“子弹—木块”模型,一般涉及两个物体,且二者产生相对运动,使用隔离法分析二者的受力情况和确定它们的运动情况是分析该类问题的基础. 由于这类问题中往往伴随着临界问题和多过程问题,使得此类问题变得较为复杂. 但对于该模型只要能把握恰当的方法和知识要点,在分析该物理模型时很多问题都能迎刃而解,具体分析如下:
一、高考考情分析
“子弹-木块”模型是高考命题的热点之一,对于该模型的考查通常具有以下特点:
1.“子弹-木块”类问题,具有涉及考点多(运动学公式、牛顿运动定律、功能关系等),情境丰富,设问灵活,解法多样,思维量高等特点,是一类选拔功能极强的试题,也是新课标力学常考的试题.
2. 根据新课程标准分析,在新一轮的高考命题中,要求考生利用“子弹-木块”模型来分析和解决实际问题的可能性比较大,这也是新一轮高考中对该知识点考查時的一个命题趋势和命题热点.
二、“子弹-木块”模型的原型再现
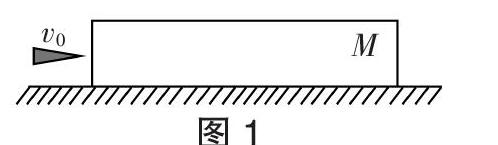
现有一质量为M的木块静止在光滑的水平面上,一质量m的子弹以初速度v0水平飞来打进木块并留在其中,如图1所示,设相互作用力为f:
问题1:子弹、木块相对静止时的速度v
由动量守恒定律得:mv0=(M+m)v
解得:v=■v0
问题2:子弹在木块内运动的时间
对木块由动量定理得:
f·t=Mv-0(或对子弹:-f·t=mv-mv0)
解得:t=■
问题3:子弹、木块发生的位移以及子弹打进木块的深度
如图2所示,子弹、木块的对地位移以及两者的相对位移分别为S1、S2和 S相,由动能定理:
对子弹有:-f·s1=■mv2-■m■
解得:s1=■
对木块有:fs2=■Mv2
解得:s2=■
打进深度就是相对位移:
d=S相=S1-S2=■
问题4:系统损失的机械能、系统增加的内能
系统损失的机械能为:E损=■m■-■(M+m)v2=■
系统损失的机械能转化为了内能,由问题3可得:
Q=f(s1-s2)=f·s相=■
说明:相互作用力与相对位移(或路程)的乘积等于系统机械能的减小,这是一个重要关系,通常都可直接运用.
问题5:子弹、木块两者的v-t图像
子弹做匀减速直线运动,木块做匀加速直线运动,两者的v-t图像如图3所示.
问题6:要使子弹不穿出木块,木块至少多长(v0、m、M、f一定)
设子弹进入木块的深度为L,由动能定理得:
fL=■m■-■(M+m)v2
解得:L=■
三、“子弹-木块”模型的推广
根据“子弹-木块”模型的受力特征以及运动特点,将该模型进行推广,从而得到以下的“板-块”模型,如图4,其基本物理情景是:质量为M的木板静止于光滑的水平面上,一质量为m的滑块以速度v0从木板的左端滑上木板.
“子弹-木块”推广模型(即“板-块”模型)的基本特征分析如下:
1.模型特点:涉及两个(或多个)物体,并且物体间存在相对滑动.
2.摩擦力方向的特点.
(1)若两个物体同向运动,且两个物体“一快一慢”,则“快”的物体受到的另一个物体对它的摩擦力为阻力,“慢”的物体受到的另一个物体对它的摩擦力为动力.
(2)若两个物体反向运动,则每个物体受到的另一个物体对它的摩擦力均为阻力.
3.运动特点.
(1)滑块由滑板的一端运动到另一端的过程中,若滑块和滑板同向运动,位移大小之差等于板长(此时类似于追击问题);反向运动时,位移大小之和等于板长(此时类似于相遇问题). 设板长为L,滑块位移大小为x1,滑板位移大小为x2:
同向运动时,如图5所示:L=x1-x2
反向运动时,如图6所示:L=x1+x2
(2)若滑块与滑板最终相对静止,则它们的末速度相等.
四、分析“子弹-木块”模型的奇思妙计
五、“子弹-木块”模型四大经典题型
对于“滑块-滑板”模型的问题归纳起来,主要有以下几种典型的题型:
题型一:“子弹-木块”模型与v-t图像的综合
【典列1】一长木板置于粗糙水平地面上,木板左端放置一小物块. 在木板右方有一墙壁,木板右端与墙壁的距离为4.5 m,如图7所示. t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1 s时木板与墙壁碰撞(碰撞时间极短). 碰撞前后木板速度大小不变,方向相反,运动过程中小物块始终未离开木板. 已知碰撞后1 s时间内小物块的v-t图像如图8所示. 木板的质量是小物块质量的15倍,重力加速度大小g取10 m/s2. 求:
(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;
(2)木板的最小长度;
(3)木板右端离墙壁的最终距离.
【解析】(1)规定向右为正方向. 木板与墙壁相碰前,小物块和木板一起向右做匀变速运动,设加速度为a1,小物块和木板的质量分别为m和M. 由牛顿第二定律有:
-μ1(m+M)g=(m+M)a1
由图可知,木板与墙壁碰前瞬间的速度v1=4 m/s,由运动学公式得:
v1=v0+a1t1
S0=v0t1+■a1 ■
式中,t1=1 s,S0=4.5 m是木板碰前的位移,v0是小物块和木板开始运动时的速度.
联立 式和题给条件得:μ1=0.1
在木板与墙壁碰撞后,木板以-v1的初速度向左做匀变速运动,小物块以v1的初速度向右做匀变速运动. 设小物块的加速度为a2,由牛顿第二定律有:-μ2mg=ma2
由图可得:a2=■
式中,t2=2 s,v2=0联立?譽?訛?譾?訛式和题给条件得:μ2=0.4
(2)设碰撞后木板的加速度为a3,经过时间?驻t,木板和小物块刚好具有共同速度v3. 由牛顿第二定律及运动学公式得:μ2mg+μ1(m+M)g=Ma3
v3=-v1+a3
v3=v1+a2
碰撞后至木板和小物块刚好达到共同速度的过程中,木板运动的位移为
S1=■·
小物块运动的位移为S2=■·
小物块相对木板的位移为?驻S=S2-S1
式,并代入数值得?驻S=0.6 m
因为运动过程中小物块没有脱离木板,所以木板的最小长度应为0.6 m.
(3)在小物块和木板具有共同速度后,两者向左做匀变速运动直至停止,设加速度为a4,此过程中小物块和木板运动的位移为S3. 由牛顿第二定律及运动学公式得:
(M+m)g=(m+M)a4
0-■=2a4S3
碰后木板运动的位移为:S=S1+S3
式,并代入数值得:S=-6.5 m
木板右端离墙壁的最终距离为6.5m.
【答案】(1)0.1 0.4;(2)6.0 m;(3)6.5 m
【方法技巧】在用动力学观点分析“子弹-木块”模型问题时,一般采用以下思路进行:
题型二、“子弹-木块”模型中的“临界问题”
【典例2】(2017·全国卷Ⅲ)如图9所示,两个滑块A和B的质量分别为mA=1 kg和mB=5 kg,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4 kg,与地面间的动摩擦因数为μ2=0.1. 某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3 m/s. A、B相遇时,A与木板恰好相对静止. 设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10 m/s2. 求:
(1)B与木板相对静止时,木板的速度;
(2)A、B开始运动时,两者之间的距离.
【解析】(1)滑块A和B在木板上滑动时,木板也在地面上滑动. 设A、B和木板所受的摩擦力大小分别为f1、f2和f3,A和B相对于地面的加速度大小分别为aA和aB,木板相对于地面的加速度大小为a1. 在滑块B与木板达到共同速度前有:
f1=μ1mA g ①
f2=μ1mB g ②
f3=μ2(m+mA+mB)g③
由牛顿第二定律得:
f1=mAaA④
f2=mBaB⑤
f2- f1- f3=ma1⑥
设在t1时刻,B与木板达到共同速度,其大小为v1. 由运动学公式有:
v1=v0-aB t1 ⑦
v1=a1t1 ⑧
联立①②③④⑤⑥⑦⑧式,代入已知数据得:v1=1 m/s ⑨
(2)在t1时间间隔内,B相对于地面移动的距离为:
sB=v0t1-■aBt12⑩
设在B与木板达到共同速度v1后,木板的加速度大小为a2. 对于B与木板组成的体系,由牛顿第二定律有:
f1+f3=(mB+m)a2
由①②④⑤式知,aA=aB;再由⑦⑧式知,B与木板达到共同速度时,A的速度大小也为v1,但运动方向与木板相反. 由题意知,A和B相遇时,A与木板的速度相同,设其大小为v2. 设A的速度大小从v1变到v2所用的时间为t2,则由运动学公式,
对木板有:v2=v1-a2t2
对A有:v2=-v1+aAt2
在t2时间间隔内,B(以及木板)相对地面移动的距离为:
s1=v1t2-■a2■
在(t1+t2)时间间隔内,A相对地面移动的距离为:
sA=v0(t1+t2)-■aA(t2+t1)2
A和B相遇时,A与木板的速度也恰好相同. 因此A和B开始运动时,兩者之间的距离为:s0=sA+s1+sB
联立以上各式,并代入数据得:s0=1.9 m
【答案】(1)1 m/s (2)1.9 m
【方法技巧】在“子弹-木块”模型中的“临界问题”时其思维流程如下:
题型三、“子弹-木块”模型与实际生活的结合
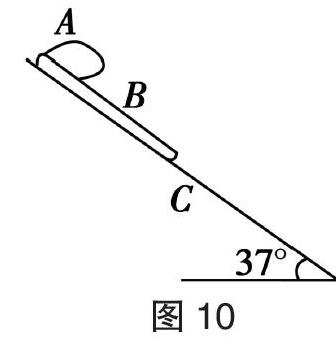
【典例3】下暴雨时,有时会发生山体滑坡或泥石流等地质灾害. 某地有一倾角为θ=37°(sin 37°=35)的山坡C,上面有一质量为m的石板B,其上下表面与斜坡平行;B上有一碎石堆A(含有大量泥土),A和B均处于静止状态,如图10所示. 假设某次暴雨中,A浸透雨水后总质量也为m(可视为质量不变的滑块),在极短时间内,A、B间的动摩擦因数μ1减小为38,B、C间的动摩擦因数μ2减小为0.5,A、B开始运动,此时刻为计时起点;在第2 s末,B的上表面突然变为光滑,μ2保持不变. 已知A开始运动时,A离B下边缘的距离l=27 m,C足够长. 设最大静摩擦力等于滑动摩擦力. 取重力加速度大小g=10 m/s2. 求:
(1)在0~2 s时间内A和B加速度的大小;
(2)A在B上总的运动时间.
【解析】(1)在0~2 s内,A和B受力如图11所示:
由滑动摩擦力公式和力的平衡条件得:
f1=μ1N1 ①
N1=mgcos θ ②
f2=μ2N2 ③
N2=N1+mgcos θ ④
以沿着斜面向下为正方向,设A和B的加速度分别为a1,a2. 由牛顿第二定律可得:
mgsin θ-f1=ma1⑤
mgsin θ-f2+f1=ma2 ⑥
联立以上各式可得:a1=3 m/s2⑦
a2=1 m/s2 ⑧
(2)在t1=2 s,设A和B的速度分别为v1,v2,则:
v1=a1t1=6 m/s ⑨
v2=a2t1=2 m/s ⑩
t>t1时,设A和B的加速度分别为a′1,a′2,此时A、B之间摩擦力为零,同理可得:
a′1=6 m/s2
a′2=-2 m/s2
即B做匀减速,设经时间t2,B的速度为零,则:
v2+a′2t2=0
联立可得:t2=1 s
在t1+t2时间内,A相对于B运动的距离为:
s=(■a1 ■+v1t2+■■■)-(■a2 ■+v2t2+■■■)=12 m<27 m
此后B静止不动,A继续在B上滑动,设再经时间t3后,A离开B,则有:
l-s=(v1+a′1t2)t3+12a′1t23
可得,t3=1 s(另一解不合题意,舍去)
设A在B上的运动时间为t总,t总=t1+t2+t3=4 s
【答案】(1)3 m/s2 1 m/s2;(2)4 s
【方法技巧】在分析实际生活中的“子弹-木块”模型时一定要结合实际找出“子弹”和“木块”,然后用相关的原理和知识来分析实际生活中的“子弹-木块”模型. 更值得提醒的是用所学知识解决实际生活中的问题是新高考的命题热点.
题型四、“子弹-木块”与电学知识的结合
【典列4】如图12所示,电容器固定在一个绝缘座上,绝缘座放在光滑水平面上. 平行板电容器板间距离为d,电容为C. 右极板有一个小孔,通过小孔有一长为■d的绝缘杆,左端固定在左极板上,电容器极板连同底座、绝缘杆总质量为M. 给电容器充入电量Q后,有一质量为m、带电量+q的环套在杆上以某一初速度v0对准小孔向左运动(M=3m). 设带电环不影响电容器板间电场的分布,电容器外部电场忽略不计. 带电环进入电容器后距左板最小距离为■d,试求:
(1)带电环与左极板间相距最近时的速度;
(2)带电环受绝缘杆的摩擦力.
【解析】(1)带电环距左板最近时,类似于子弹,木块相对静止时由动量守恒定律得:mv0=(M+m)v
解得:v=■v0=■v0
(2)带电环与其余部分间的相互作用力,做功的有电场力:
F电=qE=■
摩擦力f由能的转化和守恒定律得:
F电·■+f(■-■)=■m■-■(M+m)v2
解得:f=■-■
【方法技巧】“子弹-木块”模型这类问题,關键是要抓住动量与能量这两条主线,弄清系统内参与做功的是什么力,其相对位移(或相对路程)是多少,从而顺利建立等量关系,“子弹-木块”模型问题从形式上、条件上、问法上都有不同之处,但解决问题的思路却是相同的,这就要求我们要吃透基本模型基本特征、规律.
六、小结
综上所述,“子弹-木块”模型的分析思想和方法具有普遍性和可操作性,一方面从子弹和木块构成系统的相互作用拓宽到任何两个物体构成系统的相互作用,系统不受外力或某方面不受外力或合外力为零,则系统动量守恒. 另一方面从子弹和木块的系统内力,即一对摩擦力做功,拓宽一对弹力做功、重力做功、电场力做功、磁场力做功,实现了系统能量的转移和转化. 对相互作用的物体系统的分析,应用了子弹打击木块模型的分析思想和方法,操作性强、解答规范简单,所以说对学生分析问题有较好的指导作用.
责任编辑李平安

