2021年高考不等式命题探析
王佩其


《不等式》是高中数学的必修内容,也是历年高考的必考内容. 不等式的性质应用、不等式的解法、简单的线性规划和基本不等式的应用,历来是高考命题的重点. 从近三年的新课标高考真题来看,不等式高考命题主要有以下三个特点:(1)选择、填空题中的考查以简单的线性规划与不等式性质为主,重点求目标函数的最值,有时也与其它知识交汇考查;(2)在填空题中主要考查利用基本不等式求多元的最值和不等式的实际应用;(3)不等式的解法多与集合、函数、解析几何、导数交汇考查. 以史为鉴看高考命题走向,那么2021年高考不等式考什么?本文加以预测,供同学们参考.
考向一:不等式的性质
高考对不等式性质的考查一般以选择题的形式出现,难度一般.
预测题1 (1)已知实数a,b满足a>b,则下列不等式中恒成立的是( )
A. a2>b2B.■<■C. |a|>|b|D.πa>πb
(2)(多选题)下列四个命题中正确命题有( )
A.若a>|b|,则a2>b2
B.若a>b,c>d,则a-c>b-d
C.若a>b,c>d,则ac>bd
D.若a>b>0,c<0,则■>■
答案(1)D; (2)AD.
解析(1)A选项不正确,当a=1,b=-2时,不等式就不成立;
B选项不正确,因为a=1,b=-2时,不等式就不成立;
C选项不正确,因为a=1,b=-2时,不等式就不成立;
D选项正确,因为y=πx是一个增函数,故当a>b时一定有πa>πb.
(2)①∵ a>|b|,∴ a2>b2,故正确;
②∵ a>b,c>d,∴ a+c>b+d,因此a-c>b-d不正确;
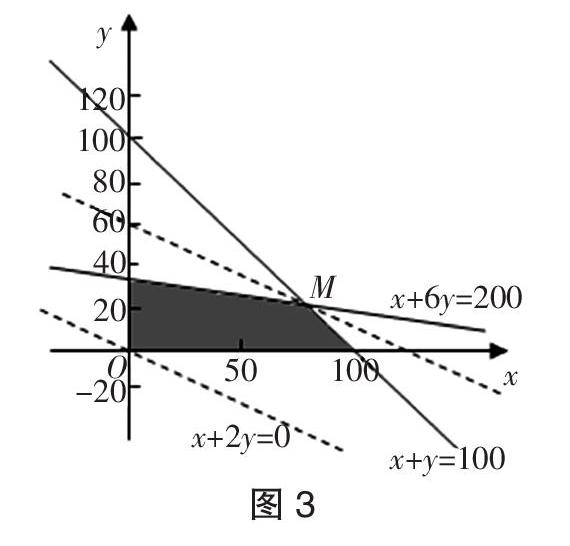
③取a=2,b=1,c=-2,d=-3,满足a>b,c>d,但是ac=-4 ④∵a>b>0,c<0,∴■>■>0,-c>0,∴■>■,∴■>■,故正确. 点评(1)数与式的大小比较主要有作差法和函数单调性法;(2)不等式的性质是不等式变形的依据,每一步变形都要严格依照性质进行,千万不可想当然. 预测训练1 (1)已知a,b,c∈R,3a=2,4b=5,5c=4,则下列不等關系中正确的是( ) A. a (2)(多选题)已知0 A. ab>acB.■>■C. logba>logcaD.■>■ 考向二:解不等式 高考对解不等式的考查不会单独命题,往往与其它知识综合在一起,考查解不等式的综合应用,题型以选择题与填空题为主,难度中等. 预测题2 (1)集合P={x|■>0},Q={y|y=■},则P∩Q=( ) A.(1,2]B. [1,2]C.(-∞,-3)∪(1,+∞)D. [1,2) (2)函数f(x)=2sinx+3x,若f(6-a2)+f(a)>0,则满足不等式的实数a的取值范围是______________. 答案(1)A;(2)(-2,3). 解析(1)解■>0得x<-3或x>1,即P=(-∞,-3)∪(1,+∞);令4-x2≥0,解得-2≤x≤2,所以0≤■≤2,即Q=[0, 2],所以P∩Q=(1, 2]. (2)因为函数f(x)=2sinx+3x的定义域为R,且满足f(-x)= -f(x),所以它为奇函数. 又f ′(x)=2cosx+3>0,所以这个函数又是增函数,于是由f(6-a2)+f(a)>0得6-a2+a>0.解得-2 点评(1)解一元二次不等式,可先化为一般形式ax2+bx+c>0(a>0),再结合相应二次方程的根及二次函数图像确定一元二次不等式的解集.而分式不等式一般可转化为整式不等式来解; (2)对于含指数、对数的不等式,可利用指数、对数函数的单调性将其转化为整式不等式求解; (3)对于有函数与导数背景的不等式,则可灵活利用函数的性质(单调性、奇偶性、对称性等)与图像求解. 预测训练2 (1)已知集合A={x∈Z|x2-2x-3≤0},B={y|22y-1≥■},则A∩B中的元素之和是() A. 3 B. 4 C. 5 D. 6 (2)已知定义在R上的奇函数f(x),其导函数为f ′(x),当x≥0时,恒有■f ′(x)-f(-x)≤0,则不等式x3f(x)-(1+2x)3 f(1+2x)<0的解集为_________. 考向三:简单的线性规划 高考对简单的线性规划的考查主要涉及两类问题:一是求目标函数的最大值或最小值;二是求解含有参数的线性规划问题.以选择题与填空题为主,难度上看为中档题. 预测题3 (1)若实数x,y满足约束条件2x-3y+6≥0,y≥2|x-1|,则z=3x+y的最小值为( ) A. 13 B. 3 C. 2 D. 1 (2)若不等式组|x|+|y|≤2,y+2≤k(x+1)表示的平面区域是三角形,则实数k的取值范围是_______. 答案(1)C;(2)k<-2或0 解析(1)∵ y=2|x-1|=2x-2,x≥12-2x,x<1∴该不等式组对应的平面区域,如图1所示z=3x+y可化为y=-3x+z,平移直线y=-3x,当直线过点A(0, 2)时,z取最小值,即zmin=3×0+2=2. (2)如图2所示,由于|x|+|y| ≤2表示正方形ABCD内部区域,包含边界;而y+2=k(x+1)表示一条经过点M(-1, -2),斜率等于k的直线,故当斜率k满足大于零且小于或等于MC的斜率、或者斜率k满足小于MA的斜率时,表示的平面区域是三角形,则有kMC=■,kMA=-2,故应有0 故答案为:k<-2或0 点评(1)解决线性规划问题首先要画出可行域,再注意目标函数所表示的几何意义,数形结合找到目标函数达到最值时可行域的顶点(或边界上的点),但要注意作图一定要准确,整点问题可通过验证解决. (2)确定二元一次不等式组表示的平面区域:①画线,②定侧,③确定公共部分;解线性规划问题的步骤:①作图,②平移目标函数线,③解有关方程组求值,确定最优解(或最值等). 预测训练3 (1)已知实数x,y满足约束条件x+2y-2≥0,x-2y+2≥0,x≤2,则x2+y2的取值范围是() A. [■,2■] B. [■,8] C. [■,8] D. [1,8] (2)已知实数x,y满足不等式组x-y+1≥0,x-2y+1≤0,x+y-2≤0,若目标函数z=x+ay仅在点(■,■)处取最大值,则实数a的取值范围为______. 考向4:基本不等式的应用 高考对基本不等式以及应用是C级要求,主要考查利用基本不等式求最值,方法较为灵活,难度中等偏上,以二元变量的最值问题为主,主要出现在选择题与解答题中. 预测题4 (1)若log3(2a+b)=1+log■■,则a+2b的最小值为( ) A. 6 B.■ C. 3 D.■ (2)已知a>0,b>0,且a+12b+6≤■+■,则■的最大值为______. 答案(1)C;(2)■. 解析(1)∵ log3(2a+b)=1+log■■, ∴ log3(2a+b)=1+log3ab=log3(3ab),∴2a+b=3ab,且a>0,b>0, ∴■+■=3,∴ a+2b=■(a+2b)(■+■)=■(1+■+■+4)=■+■(■+■)≥■+■·2■=3,當且仅当■=■且■+■=3即a=b=1时,等号成立. (2)∵ a>0,b>0,且a+12b+6≤■+■,∴(a+12b+6)(■+■)≤(■+■)2. ∵(a+12b+6)(■+■)=3+■+■+■+12+■=15+(■+■)+6(■+■), ∴(a+12b+6)(■+■)≥15+2■+6(■+■)=27+6(■+■),当且仅当a=6b时取等号. 令■+■=t(t>0),原不等式转化为27+6t≤t2,解得t≥9. ∴■=■=■≤■. 点评(1)用基本不等式■≥■求最值时,要注意“一正、二定、三相等”,一定要明确什么时候等号成立,要注意“代入消元”“拆、拼、凑”“1的代换”等技巧的应用. (2)利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:一是对条件使用基本不等式,建立所求目标函数的不等式求解;二是条件变形,进行“1”的代换求目标函数最值. 预测训练4 (1)设实数a、b满足b>0,且a+b=2. 则■+■的最小值是( ) A.■ B.■ C.■ D.■ (2)设x>0,y>0,x+2y=4,则■的最小值为 __________. 考向5:不等式恒成立或有解问题 含参数不等式的恒成立或有解的问题,是近几年高考的热点. 它往往以函数、数列、三角函数、解析几何为载体具有一定的综合性,解决这类问题,主要是运用等价转化的数学思想. 含参数不等式的恒成立或有解问题常根据不等式的结构特征,恰当地构造函数,等价转化为含参数的函数的最值讨论. 这类问题一般以选择题或填空题形式出现,难度中等偏上. 预测题5 (1)已知a>0,b>0,若不等式■+■≥■恒成立,则m的最大值为( ) A. 10 B. 12 C. 16 D. 9 (2)设函数f(x)=x2-3x+a,已知?埚t0∈(1,3],使得当x∈[1, t0] 时,f(x)≤0有解,则实数a的取值范围是______. 答案(1)D;(2)(-∞,■] . 解析(1)由已知a>0,b>0,若不等式■+■≥■恒成立,所以m≤(■+■)(a+b)恒成立,转化成求y=(■+■)(a+b)的最小值,y=(■+■)(a+b)=5+■+■≥5+2■=9,所以m≤9. (2)依题意,只需?埚x0∈[1,3],f(x0)≤0,即f(x)min=f(■)=a-■≤0,就一定?埚t0∈(1,3),使得当x∈[1,t0]时,f(x)≤0有解,故a≤■. 点评不等式在某个区间上恒成立(存在性成立)问题的转化途径 (1)f(x)≥a恒成立?圳f(x)min≥a;存在x使f(x)≥a成立?圳f(x)max≥a. (2) f(x)≤b恒成立?圳f(x)max≤b,存在x使f(x)≤b成立?圳f(x)min≤b. (3)f(x)>g(x)恒成立,令F(x)=f(x)-g(x),F(x)min>0. 预测训练5 (1)设二次函数f(x)=ax2+bx+c(a, b, c为常数). 若不等式f(x)≥2ax+b的解集为R,则■的最大值为( ) A. 2■-2B. 2■+2 C. 2■-2D. 2■+2 (2)在R上定义运算?茚∶ x?茚y=x(1-y),0 考向6:不等式的实际应用 学以致用与立德树人,是新课标的两个理念,高考命题往往借助实际问题来体现这两个理念,因此,不等式的实际应用性问题也是一个值得重视的命题方向标,题型以选择题或填空题为主,有时也会出现在解答题中,难度中等. 预测题6 国庆期间,为了满足广大人民的消费需求,某共享单车公司欲投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型车为运动型,成本为400元辆,骑行半小时需花费0.5元;B型车为轻便型,成本为2400元辆,骑行半小时需花费1元. 若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时(不足半小时按半小时计算),则当公司投放A型单车___辆、B型单车___辆时,每天获得的总收入最多. 答案 80,20. 解析根据题意,设投放A型号单车x辆,B型号单车y辆,单车公司每天可获得的总收入为Z, 则有x+y≤100,400x+2400y≤80000,x≥0,x∈Zy≥0,y∈Z即x+y≤100,x+6y≤200,x≥0,x∈Zy≥0,y∈Z……① 且Z=2×0.5x+2×y=x+2y, 画出不等式组①表示的平面区域,由x+y=100,x+6y=200,解得M(80, 20). 当目标函数Z=x+2y,经过点M(80, 20)时,Z取得最大值为80+2×20=120. 所以公司投放两种A,B型号的单车分别为80辆20辆才能使每天获得的总收入最多,最多为120元. 点评用线性规划的方法来解决实际问题:先根据问题的需要选取起关键作用的关联较多的量用字母表示,进而把问题中所有的量都用这两个字母表示出来,建立数学模型,再画出表示的区域. 预测训练6 张辉同学大学毕业后自主创业,办了一家金属加工厂. 已知工厂每天的固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为a元时,生产x件产品的销售收入为R(x)=-■x2+500x(元),P(x)为每天生产x件产品的平均利润(平均利润=总利润/总产量). 那么每天生产量为____件时,平均利润P(x)取得最大值,最大值为______元. 本文最后提醒同学们,不等式作为新课标高考的C级要求考点,不仅考查不等式知识的本身,命题者更青睐于对不等式的“工具性”的考查,尤其是综合性问题中的最值问题,需引起大家的格外关注. 预测训练答案与解析 1. (1)D.【解析】∵3a=2,4b=5,5c=4,∴a=log3 2=log9 4 (2)CD【解析】∵ 0 2. (1)D. 解不等式x2-2x-3≤0,x∈Z,可得A={-1,0,1, 2,3}. 解不等式22y-1≥■,可得B=[0,+∞). ∴ A∩B={0,1,2,3},故元素之和为6. (2){x|-1 3. (1)B.【解析】由約束条件作出可行域是由A(2, 0),B(0, 1),C(2, 2)三点所围成的三角形及其内部,如图4中阴影部分,而x2+y2可理解为可行域内的点到原点距离的平方,显然原点到AB所在的直线x+2y-2=0的距离是可行域内的点到原点距离的最小值,此时x2+y2=OD2=(■)2=■,点C到原点的距离是可行域内的点到原点距离的最大值,此时x2+y2=22+22=8. 所以x2+y2的取值范围是[■,8]. (2)(1,+∞).【解析】作出可行域如图5所示, 目标函数z=x+ay,令y=0,则z=x,即目标函数仅在过A点时,在x轴上的截距最大,如图旋转l并观察,则l的斜率k∈(-1,0),即-1<-■<0,得a>1. 4.(1)C .【解析】由题意可知,a≠0. 当a>0时,■+■=■+■=■+■+■≥■+ 2■=■, 当且仅当■=■且a+b=2,即a=■,b=■时取等号, 当a<0时,■+■=-■-■=-■+(-■)+(-■)≥-■+2■=■, 当且仅当■=■且a+b=2时取等号. 综上可得,■+■的最小值为■. (2)9. 【解析】■=■=■=1+■. 又x+2y=4≥2■,即xy≤2,当且仅当x=2,y=1等号成立,故原式≥9. 故填9 5. (1)A. 【解析】由题设可得ax2+(b-2a)x+c-b≥0对一切实数恒成立,取x=1可得c-a≥0且判别式(b-2a)2-4a(c-b)≤0,a>0,c-a≥0对一切实数恒成立,即b2+4a2≤4ac,a>0,c-a≥0对一切实数恒成立,所以■≤■,令c-a=t≥0,则c=a+t代入■≤■=■=■≤■=2■-2(当且仅当c=2a取等号),故■的最大值是2■-2. (2)(-∞,■). 【解析】由题意可得(ax-2)?茚(1-x)=(ax-2)[1-(1-x)]=ax2-2x<-3a在(0,2]上有解,所以a(x2+3)<2x即a<■在(0, 2]上有解. 又■=■≤■=■,当且仅当x=■时,等号成立,所以■在(0,2]的最大值为■,所以实数a的取值范围是 {a|a<■}. 6. 400,200. 【解析】由题意得,总利润为-■x2+500x-100x-40000=-■x2+400x-40000. 于是P(x)=■ = -■x-■+400 ≤-2■+400=-200+400=200,当且仅当■x=■即x=400时等号成立. 故每天生产量为400件时平均利润最大,最大值为200元. 责任编辑 徐国坚

