化归与转化思想在高考数学解题中的运用
罗文军
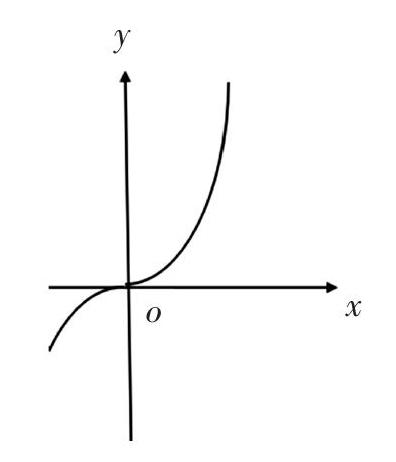


化归与转换的思想,就是在研究和解决数学问题时采用某种方式,借助某种函数性质、图像、公式或已知条件将问题通过变换加以转化,进而达到解决问题的思想等价转化总是将抽象转化为具体,复杂转化为简单、未知转化为已知,通过变换迅速而合理的寻找和选择问题解决的途径和方法.
1.化归与转化的思想方法:解决数学问题时,常遇到一些问题直接求解较为困难,通过观察、分析、类比、联想等思维过程,选择运用恰当的数学方法进行变换,将原问题转化为一个新问题(相对来说,对自己较熟悉的问题),通过新问题的求解,达到解决原问题的目的.
2.化归与转化应遵循的基本原则:
(1)熟悉化原则;(2)简单化原则;(3)和谐化原则;(4)直观化原则;(5)正难则反原则
3.化归与转化的途径:
(1)从问题的反面思考;(2)局部向整体的转化;(3)未知向已知转化;(4)固定向重组的转化;(5)抽象向具体转化;(6)个别向一般的转化;(7)数向形的转化;(8)定量向定性的转化;(9)主元向辅元的转化.
以下结合一些经典试题,谈谈化归与转化思想在高三解题中的运用.
题型一:化归与转化思想简单化原则的体现
化归与转化思想简单化原则在解题中的体现主要有:(1)将比较代数式的大小的问题,运用同构法,通过构造函数,化归为利用函数的单调性根据自变量的大小比较函数值的大小或者根据函数值的大小比较自变量的大小;(2)将概率与统计问题化归为集合间的基本关系与基本运算问题.
例1. 若2a+log2a=4b+2log4b,则( )
A. a>2bB. a<2bC. a>b2 D. a 【解析】由指数幂的运算性质和对数的运算性质可得,2a+log2a=4b+2log4b=22b+log2b, 又因为22b+log2b<22b+log22b=22b+1+log2b, 所以2a+log2a<22b+log22b. 令f(x)=2x+log2x,由指数函数和对数函数性质以及函数单调性的性质可得f(x)在(0, +∞)上单调递增,由f(a) 【评析】本题考查了指数幂和对数的运算,函数的单调性的性质,构造函数后,把问题化归与转化为根据函数单调性,由函数值的大小比较自变量的大小,体现了化归与转化思想的简单化原则. 例2. 设命题p ∶ 4x-3≤1,命题 q∶ x2-(2a+1)x+a(a+1)≤ 0. 若?劭 p是?劭 q的必要不充分条件,则实数a 的取值范围是__________. 【解析】由4x-3≤1,得■≤x≤1,记A={x│■≤x≤1}; 由 x2-(2a+1)x+a(a+1)≤0,可得 a≤x≤a+1,记 B={x│a≤x≤a+1}. 因为?劭 p是?劭 q的必要不充分条件,所以q是p的必要不充分条件,所以p是q的充分不必要条件,所以A?芴B,所以a≤■,a+1≥1,解得0≤a≤■,所以实数a的取值范围是[0,■]. 【评注】本题的解答中,先把两个命题中的不等式的解集分别用集合A和集合B表示,再由?劭 p是?劭 q是的必要不充分条件转化为p是q的充分不必要条件,再转化为集合A为集合B的真子集,解得a的范围. 题型二:化归与转化思想直观化原则的体现 化归与转化思想直观化原则在解题中的体现主要有:(1)画出函数图像后,利用函数图像研究函数的性质,进而直观的解决与函数有关的问题;(2)立体几何问题中,将立体问题平面化,画出轴截面或者中截面,利用平面几何问题破解题目. 例3. 设a, b∈R,则|“a>b”是“aa>bb”的( ) A. 充要不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充要也不必要条件 【解析】构造函数f(x)=xx=x2,x≥0-x2,x<0 函數图像如图1, 由图像可知f(x)=xx在R上单调递增. 当a>b时,f(a)>f(b),即aa>bb,a>b?圯aa>bb. 当f(a)>f(b),即aa>bb时, a>b,aa>bb?圯a>b, 所以a>b?圳aa>bb,“a>b”是“aa>bb”的充要条件,故选C. 【评注】本题是一道比较复杂的充分必要条件问题,通过观察题目,通过类比和联想,运用化归与转化思想,构造函数f(x)=xx后,画出这个函数的图像,运用图像法判断这个函数在其定义域R上为单调递增函数,把a和b看成这个函数的两个自变量,aa和bb分别看成这个函数的函数值f(a)和f(b),由增函数的性质可以得出,a>b?圳aa>bb,所以a>b是aa>bb的充分必要条件,体现了化归与转化思想的简单化和直观化原则. 例4. 已知某个机械零件是由两个有公共底面的圆锥组成的,且这两个圆锥有公共点的母线互相垂直,把这个机械零件打磨成球形,该球的半径最大为1,设这两个圆锥的高分别为h1,h2,则h1+h2的最小值为________. 【答案】2■. 【解析】由题意可知,打磨后所得半径最大的球是由这两个圆锥构成的组合体的内切球,内切球的半径R=1,如图为这个组合体的轴截面示意图,圆O为内切球的轴截面, E, F, G, H分别为切点,连接OA, OB, OC, OD, OE, OF, OG, OH,由题意可知AB⊥BC, AD⊥DC,AC=h1+h2,R=OE=OF=OG=OH=1,则S四边形ABCD=S△AOB+S△BOC+S△COD+S△AOD,即AB×BC=■R×AB+■R×BC+■R×CD+■R×AD =■R(2AB+2BC)=R(AB+BC),所以AB×BC=AB+BC.
由基本不等式可得AB×BC=AB+BC≥2■,则AB×BC≥4,当且仅当AB=BC时等号成立.
所以(h1+h2)2=AC2=AB2+BC2≥2AB×BC≥8,当且仅当AB=BC时等号成立,故h1+h2 的最小值为2■.
【评注】本题的解答运用了化归与转化的思想,通过研究组合体和其内切球的轴截面,把空间立体几何问题化归为平面几何问题,做到了把问题直观化的原则.
题型三:化归与转化思想熟悉化原则的体现
化归与转化思想熟悉化原则在解题中的体现主要有:(1)不等式题目中,把含一个参数的不等式恒成立问题,通过分离变量,化归为求函数在给定区间上的最值问题;(2)立体几何题目中,利用长方体或者正方体模型,把一些三棱锥、四棱锥和三棱柱的外接球问题化归为熟悉的长方体或者正方体的外接球问题.
例5. 若对任意的x∈(0, +∞),ax-ln(2x)≥1恒成立,则实数a的最小值是_______
【解析】由已知可得,对任意的x∈(0,+∞),a≥■恒成立,
令g(x)=■,g′(x)=■=■,
令g′(x)=0,则1-ln(2x)=0,则x=■,
当0
所以当x=■时, g(x)取得最大值 g(x)max =g(■)=■=■,
所以a≥■,所以a的最小值为■.
【评注】本题的解答运用了分离变量法,分离变量后,构造函数后,把a≥g(x)在(0, +∞)上恒成立等价转化为a≥
[g(x)]max(x∈(0,+∞)),转化为求函数g(x)在(0, +∞)上的最大值问题,g(x)的最大值即为a的最小值,本题体现了化归与转化思想的熟悉化原则.
例6. 设数列 {an} 的前n项为Sn,a1=1,当n≥2时,an=2anSn-2S2n.
(1)求数列 {an} 的通项公式;
(2)是否存在正数k,使(1+S1)(1+S2)…(1+Sn)≥k■对一切正整数n都成立?若存在,求k的取值范围,若不存在,请说明理由.
解:(1)因为当n≥2时,an=2anSn-2S2n,
所以an=■,n≥2,所以(Sn-Sn-1)(2Sn-1)=2S2n,
所以Sn-Sn-1=-2SnSn-1,所以■-■=2,n≥2,
所以数列{■}是以■=1为首项,以2为公差的等差数列,
所以■=1+2(n-1)=2n-1,所以Sn=■,
所以,当n≥2时,an=Sn-Sn-1=■-■=-■,
因为a1=S1=1,所以an=1, n=1-■. n≥2
(2)设f(n)=■,
则■=■=■>1,
所以f(n)在 n∈N?鄢上递增,要使f(n)≥k恒成立,只需要f(n)min≥k,
因为f(n)min =f(1)=■,所以0 【评注】第(1)问运用了数列的前n项和Sn与通项an之间的关系an=Sn-Sn-1(n≥2),把an 转化为Sn-Sn-1,再合并同类项后运用取倒数法,再根据等差数列的定义得出数列{■}的通项公式,再得出数列{an}的通项公式;第(2)问分离变量后构造函数f(n),用作商法判断f(n)的单调性,把不等式f(n)≥k在n∈N?鄢上恒成立等价转化为f(n)min≥k(n∈N?鄢),两问都运用到了化归与转化思想. 题型四:化归与转化思想和谐化原则的体现 化归与转化思想和谐化原则在解题中的体现主要有:(1)解三角形问题中利用正弦定理实现边角的互化;(2)在三角函数问题中,将形如y=asinx+bcosx的函数问题利用辅助角公式化归为形如y=Asin(?棕x+?渍)的函数问题;(3)解析几何中,将两直线垂直化归为斜率乘积为-1或者方向向量的数量积为0;(4)将形如?滋=■形式的最值问题,转化为动直线斜率的最值问题. 例7. △ABC的内角A, B, C的对边分别为a, b, c,已知b-c=a·cosC-c·cosA. (1)求角A; (2)若a=3,求b+2c的最大值. 【解析】(1)因为b-c=a·cosC-c·cosA, 由正弦定理可得,sinB-sinC=sinAcosC-sinCcosA, 所以sinB-sinC=sin(A-C) 所以sin(A+C)-sinC=sin(A-C), 所以sinAcosC+cosAsinC-sinC=sinAcosC-cosAsinC, 所以cosA=■,因为0 (2)由(1)可得,C=■-B, 由正弦定理得,■=■=■=2R, 所以■=■=■, 所以b=2■sinB,c=2■sin(■-B), 所以b+2c=2■sinB+4■sin(■-B)=2■(2sinB+■cosB)=2■sin(B+?漬), 其中tan?渍=■,?渍∈(0,■), 由B∈(0,■),存在B使得B+?渍=■,所以sin(B+?渍)的最大值为1, 所以b+2c的最大值为2■. 【评注】第(1)问运用正弦定理实现边转化为角,再逆用两角差的正弦公式,运用内角和定理以及诱导公式,再运用两角和的正弦公式和两角差的正弦公式,得出cosA的值,得出角A的值;第(2)问运用了正弦定理将关于边的最值问题化为角的最值问题,运用三角形内角和定理以及诱导公式,再运用辅助角公式,化为三角函数在给定范围上的最值问题;两问都运用了化归与转化思想,体现了和谐化原则.
例8. 已知函数f(x)=■,则f(■)+f(■)+f(■)+…+ f(■)的值为_____.
【解析】由于直接计算有困难,先探求一般的规律,
因为f(x)=■,所以f(1-x)=■=■=■,
所以f(x)+f(1-x)=1,
倒叙相加可得f(■)+f(■)+f(■)+…+ f(■)=1009.
【评注】本题的解答中体现了特殊问题转化为一般化,运用了化归与转化思想,先通过探究在宏观上把握问题的一般规律,再将特殊问题破解.
题型五:化归与转化思想的正难则反原则在解题中的体现
化归与转化思想的正难则反原则在高中数学解题中的体现主要有:(1)间接证明方法中的反证法在解题中的运用;(2)概率问题中对立事件和互斥事件的概率公式的运用.
例9. 等差数列{an}的前n项和为Sn,a1=1+■,S3=9+3■.
(1)求数列{an}的通项an与前n项和Sn;
(2)设bn=■(n∈N?鄢),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
【解析】(1)设公差为d,由已知得a1=■+1,3a1+3d=9+3■,
所以d=2,故an=2n-1+■,Sn=n(n+■).
(2)证明:由(1)得bn=■=n+■.
假设数列{bn}中存在三项bp、 bq、 br(p、q、r互不相等)成等比数列,则b2q=bpbr,即(q+■)2=(p+■)(r+■),
所以(q2-pr)+(2q-p-r)■=0.
因为p,q,r∈N ,所以q2-pr=0,2q-p-r=0,所以(■)2=pr,(p-r)2=0,
所以p=r,这与p≠r矛盾.
所以数列 {bn} 中任意不同的三项都不可能成为等比数列.
【评注】本题的解答的第(2)问中运用了反证法,先反设假定要证的结论不成立,而设出结论的反面成立,将这个反设作为条件,运用等比数列的定义和通项公式,通过推理,得出p=r与已知条件相矛盾,所以反设错误,所以要证明的结论成立,反证法归属于间接证明方法,第(2)问运用了化归与转化的思想.
例10. 掷一个骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+B发生的概率为____.
【答案】■.
【解析】掷一个骰子的试验有6种可能结果,依题意P(A)=■=■,P(B)=■=■,所以P(B)=1-P(B)=1-■=■,顯然A与B互斥,从而P(A+B)=P(A)+P(B)=■+■=■.
【评注】先由古典概型概率公式求出事件A和事件B的概率,再由对立事件概率公式求出事件B的对立事件B的概率,再由互斥事件概率公式,把事件A+B的概率化归为求P(A)和P(B)的和,运用了化归与转化思想.
责任编辑 徐国坚

