全桥谐振电路混合控制
李海滨,张 民,韦正怡,周明珠,丁新平
(青岛理工大学 信息与控制工程学院,山东 青岛 266520)
0 引言
随着新能源技术的发展,电动汽车充电桩越来越普及,因此大功率快速充电系统也引来许多国内外学者的关注.全桥LLC 电路的原边谐振频率可由负载的大小来调节,这样原边的开关管可以实现零电压导通(ZVS),能够有效地降低电路的损耗,提升电路的EMI.因此,低压大电流的应用场合中,全桥LLC 电路的能量转换效率更高.除此以外,全桥LLC 谐振变换器还具备开关器件的电压应力小的优点.由于全桥LLC 具备以上优点,被广泛应用于充电桩电能转换、通信电源、燃料电池中等.
传统硬开关全桥电路在大功率场合下,开关损耗大、发热严重、噪声和电磁干扰(EMI)较大[1].文献[2]的全桥LLC 虽然能够通过谐振网络的谐振来实现软开关,减少开关损耗,提升转换效率,但是该电路在负载较轻时会出现电压增益失真并且会增加电路的损耗.移相全桥电路(PSFB)在重载时候容易出现桥臂滞后的现象,进而无法实现ZVS,与此同时,副边的占空比也会出现丢失的现象.所以,通常将LLC 与移相全桥(PSFB)结合[3-4],让电路在轻载时工作在PSFB 模式,在重载时工作在LLC 谐振模式[5],但是这种混合控制要求较高的系统调节速度,若采用传统数字PI 控制器,系统的动态响应会很慢[6-9].
本文提出的基于电压外环模糊PI 控制的混合控制策略,不仅综合了上述混合控制的优势,而且能大大改善全桥LLC 谐振变换器的性能.
1 全桥LLC 谐振拓扑分析
全桥LLC 的拓扑结构见图1.

图1 全桥LLC 电路结构Fig. 1 structure of full bridge LLC
电路的电压增益可由励磁电感Lm、谐振电容Cr和谐振电感Lr的谐振以及串联等效阻抗的改变来决定.fr为Lr和Cr间的谐振频率,fm为Cr、Lm与Lr间的谐振频率,即
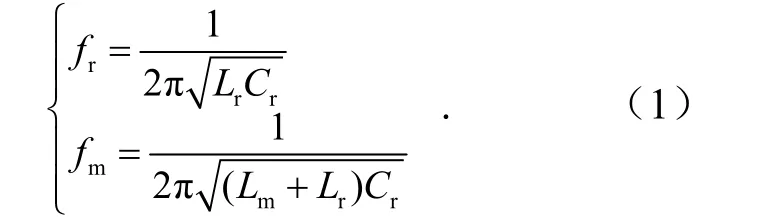
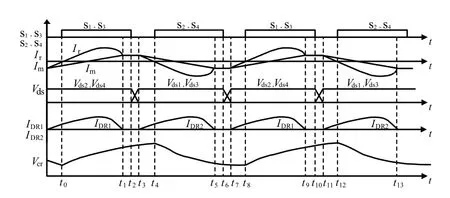
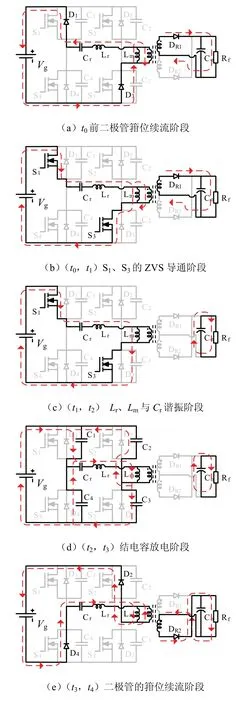
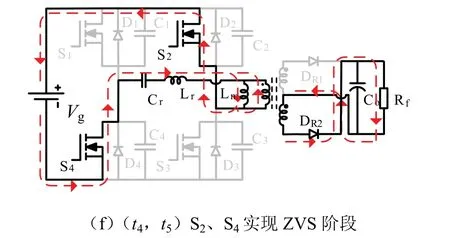
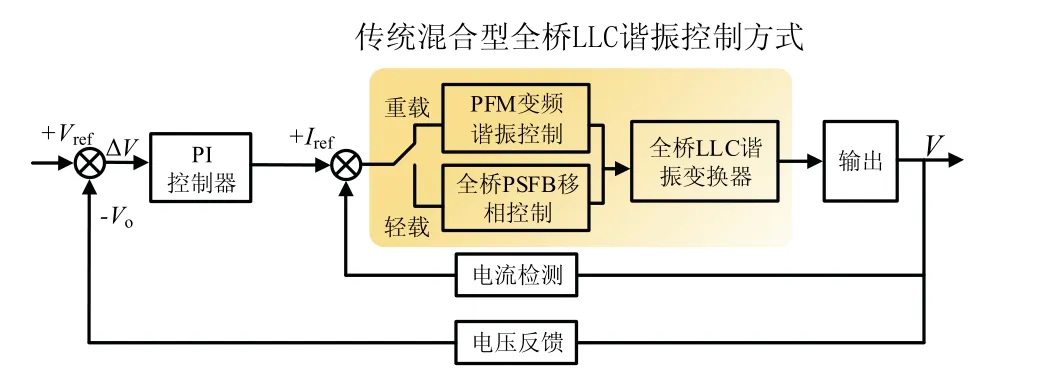
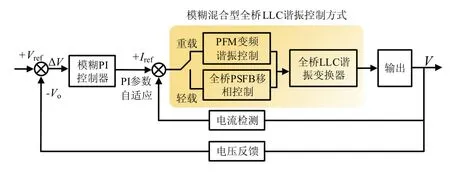
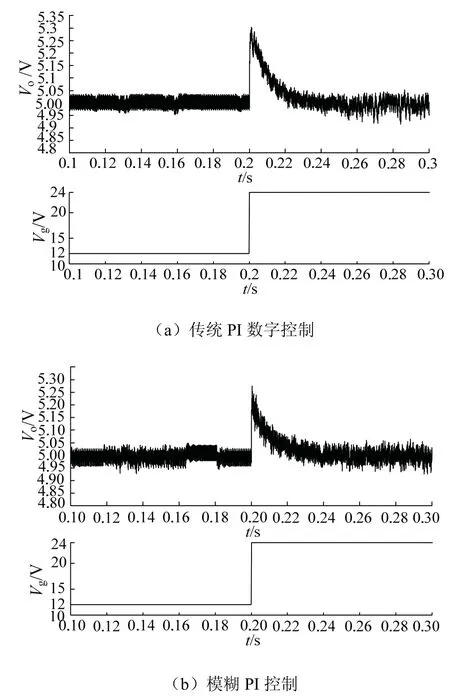
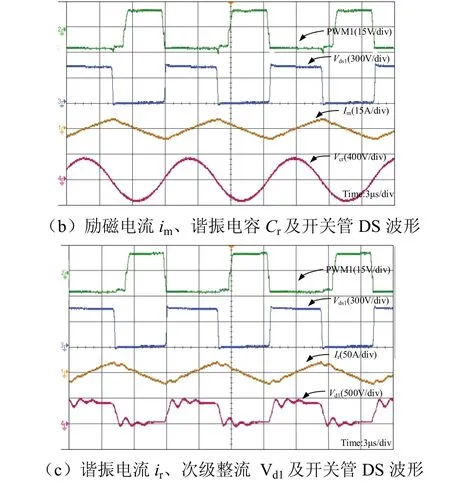
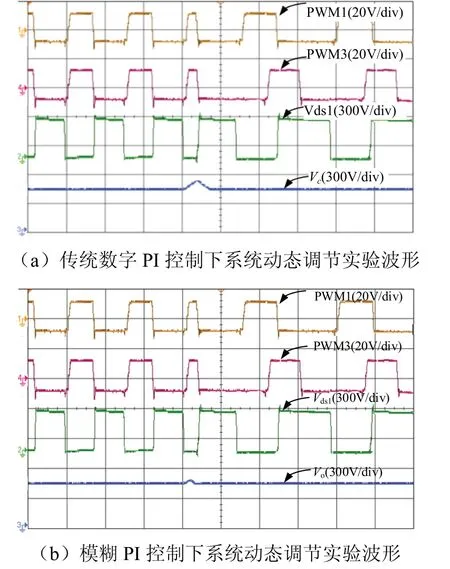
将电路工作频率分为fm 图2 为该频率下电路开关信号以及关键器件的电压电流波形,并以此波形将电路分为8 个工作阶段.由于电路的工作状态具有对称性,所以本部分主要分析正半周期的工作状态. 图2 频率范围(fm,fr)下的电路波形Fig. 2 circuit waveform with frequency in range of (fm, fr) 全桥LLC 谐振电路的工作状态见图3,电路的前5 种工作状态结合图2 对应分析.电路的后3 种工作状态图和图3(b)、图3(c)、图3(d)对称,不同之处在于将开关管从S1、S3转换到S2、S4. 阶段 0t0时刻前开关管均未导通见图 3(a).Vds1、Vds3为S1、S3的漏-源电压,当Vds1、Vds3下降到一定值时,由于二极管D1、D3续流箝位作用,实现了S1、S3的ZVS,次级二极管DR1导通,根据反射原理,励磁电感Lm的电压被箝位到NVo,励磁电流im线性减小,Lr与Cr谐振,ir正弦变化.im与ir的差值为二极管DR1的电流id1. 阶段1 (t0,t1)阶段S1、S3完成ZVS,此时Lr、Cr谐振,Lm被箝位见图3(b).ir给Cr充电,因为ir以正弦形式上升,im负向减小并反向增大,所以该状态下ir大于im.次级二极管DR1导通并向电容Co充电,流经该二极管的电流为ir与im差值.Lm的电压被箝位在NVo,当线性上升的电流im的值与ir相等时,DR1实现零电流关断(ZCS). 阶段2 (t1,t2)Lr、Lm与Cr谐振,二极管DR1实现ZCS 见图3(c).当正弦上升的ir的值等于im时,二极管DR1实现ZCS,DR1、DR2关断变压器两端停止能量传递,Lm脱箝,Lm、Lr与Cr三者谐振,Lr远小于Lm,因此本阶段的电流ir基本等于Im.电容Co对负载放电. 阶段3 (t2,t3)结电容放电见图3(d).S1、S3关断,由于电感电流不能突变,电流ir向结电容C1、C3和Cr充电,一直持续到Vds1、Vds3的值达到Vin,电容C2和C4放电,电压值降到Vds2、Vds4为零.Lr、Lm与Cr继续谐振. 阶段4 (t3,t4)二极管箝位续流见图3(e).全部开关管关断,ir保持在峰值Im,阶段3 中的结电容C2和C4放电到零后,D2、D4导通续流,S2、S4的电压被箝位到零,为S2、S4实现ZVS 做前期准备.ir和im减小,因为Lm>>Lr,所以ir的减小速度小于im,DR2导通给电容Co充电.Lm的电压被箝位到NVo,im线性减小,ir以正弦的变化形式给Cr充电. 阶段5 (t4,t5)过程中阶段S2、S4实现ZVS见图3(f).im线性减小并正向增大,ir以正弦方式减小并正向增大,im减小的速度小于ir,DR2导通将Lm箝位到NVo,Cr放电im与ir相等,DR2实现ZCS. 全桥LLC 谐振电路在轻载时会出现电压增益失真的问题.而移相全桥电路(PSFB)拥有在一定负载变化范围的情况下,抗干扰能力强、电压增益稳定且效率高等优势.根据负载的变化情况,使电路的工作模式在PSFB 模式与LLC 模式两者之间切换,可以实现电路在全负载范围内的ZC-ZVS,提高系统的抗干扰能力. 图3 全桥LLC 谐振电路工作状态Fig. 3 state of full-bridge LLC resonant circuit 全桥PSFB 的主拓扑与全桥LLC 类似,通过定频移相方式进行调节,当全桥LLC 处于空载或轻载状态时,会由PFM 变频谐振控制方式,变为PWM移相控制实现ZVS.移相全桥电路工作状态见图4. 阶段0 (t0,t1)阶段S1、S3导通,变压器原边电压Vab=Vin,励磁电感的能量传递到副边电感,原边电感的电流缓慢增加,见图4(a). 阶段1 (t1,t2)阶段S1关断、S3导通,电容C1,C4都处在谐振状态,C1充电、C4放电,一直持续到C1的电压上升到Vin,C4的电压下降到零为止.(t2,t3)阶段谐振放电结束后,S4受到D4的箝位续流,完成了ZVS,但原边电流仍然经D4续流. 阶段2 (t3,t4)阶段S3关断,ir电流方向不变,C2放电C3充电,点b电位值增大,Lm电压反向,原边电流减小使得变压器所传递的能力不能够承担负载,DR1、DR2同时导通,且流经这两个二极管的电流为输出电流的一半.当C2放电结束后,D2开始续流,此时S2实现ZVS. 阶段3 (t5,t6)阶段中正向电流下降到零,变压器原边电压Vab=-Vin,电流继续反向上升,当电流上升到一定值时,DR2导通,电路开始负半周期的功率输出过程.由于负半周期的过程与正半周期类似,所以不再赘述. 图4 移相全桥电路工作状态Fig. 4 phase shift full bridge circuit working state 传统全桥LLC 变换器可在全负载条件下实现ZV-ZCS,但在轻载下存在电压增益失真问题,变换器性能受到很大的影响.在研究过程中发现,在PFM控制下的全桥LLC 电路采用传统PI 控制,变换器工作效果一般.图5 为在PFM 控制下,采用传统PI控制框图. 图5 传统全桥LLC 谐振电路控制方式Fig. 5 traditional full-bridge LLC resonant circuit 在该控制方法下,变换器电流纹波较大,且轻载时容易出现电压增益失真,输出电压飘高以及工作频率过高引起导通损耗过大等问题. 针对这些问题,又出现了将PFM 变频控制与全桥PSFB 移相控制方式进行结合的混合控制方法,但是电压外环的控制方式任然采用了传统的PI控制技术.图6 为传统PI 控制技术与PFM、PSFB技术结合的混合控制系统结构框图. 图6 传统混合型全桥LLC 谐振电路控制系统结构Fig. 6 traditional hybrid full-bridge LLC resonant circuit control system 在该控制方式下,解决了传统全桥LLC 电路轻载出现的电压增益失真问题,降低了轻载时由于过高的开关频率出现的导通损耗过大问题,但其控制方法存在动态响应慢、系统超调大等问题. 本文采用一种混合控制方法对全桥LLC 谐振变换器进行控制.利用模糊PI 控制方法对全桥LLC变换器的外环电压进行控制.进而根据负载的变化情况采取不同的方式对谐振电路进行控制,在重载时采用PFM 变频谐振控制方式对全桥LLC 谐振变换器进行控制;在轻载时,利用全桥PSFB 移相控制方式对全桥LLC 谐振变换器进行控制.在负载变化较大时,若用传统PI 控制器来控制全桥LLC 电路,此时全桥LLC 电路的动态性能和抗干扰能力会减弱.随着负载大小的变化,主电路的工作模式也相应地进行调节,其控制系统见图7.电压外环用模糊PI 控制器来控制时,会使电路电压的动态响应加快.利用PSFB 模式来控制电路轻载或空载的工作状态,相应的重载或额定负载设计为全桥LLC 模式.对电路的输出电流进行采样,根据采样值来确定负载的大小,当轻载时,工作模式为PSFB,重载或者额定负载时,工作模式转为LLC 模式,这样就能使电路全负载可实现ZVS. 图7 模糊混合型全桥LLC 谐振电路闭环流程Fig. 7 fuzzy hybrid full-bridge LLC resonant circuit closed-loop process block 模糊PI 控制器是一种高稳态精度控制器,相比于传统PID 算法,其具有超调小、调节速度快,鲁棒性好等优点[10-11].图8 为模糊PI 混合控制原理.其中模糊控制器的设计过程: (1)确定输入输出变量.本文设定变量为输出电压误差e、误差变化率ec,输出变量为PI 参数控制系数ΔKp、ΔKi.则有 (2)确定模糊子集.本文设置的每个子集都包含7 个元素:NB、NM、NS、ZO、PS、PM、PB. (3)确定模糊控制规则. (4)经过去模糊化,得到控制输出量ΔKp、ΔKi,进而对初始PI 参数进行调整,更好地控制输出电压满足要求,实现系统的控制目标. 图8 模糊PI 混合控制系统结构Fig. 8 fuzzy hybrid control system structure 模糊PI 控制与传统的PI 控制技术相比,其可以提高系统的调节速度,另外在超调量上有独到的优势.模糊控制器采用两输入,两输出的结构.利用模糊推理得到参数ΔKP、ΔKi.将原始PI 参数按照公式(2)进行修正调整,得到实时的PI 控制参数,从而更好地实现系统的动态、静态性能. 为得到初始的PI 参数,借助小信号模型分析方法,可以推导出全桥谐振电路的小信号模型,根据得到的小信号模型,可以推导出相应的开环传递函数.应用Matlab 中的Sisotool 工具箱,按照PI 补偿方法可以得到 PI 控制器中的两个参数分别为 Kup=11,Kui=0.04. 模糊隶属函数与控制规律的设计是设计模糊控制器的核心.隶属函数的选择没有固定的模式.本文中采用三角形隶属函数,以输出电压误差e以及误差变化率ec为输入,以PI 参数调整系数ΔKp、ΔKi为输出,其中输入、输出隶属函数分布情况见图9. 文中将误差e、误差变化率ec以及ΔKp、ΔKi变化范围定义为模糊集上的论域.根据全桥谐振变换器电路技术参数的设计情况,设定e、ec以及ΔKp的论域分别为[-3,3],ΔKi的论域为[-0.3, 0.3],采用三角形隶属函数,每个子集中都包含7 个元素,分别为NB、NM、NS、ZO、PS、PM、PB,分别代表负大、负中、负小、零、正小、正中、正大. 图9 隶属函数分布Fig. 9 membership function distribution 模糊化处理过程:输入变量定义为误差e和误差变化率ec,输出变量定义为ΔKp和ΔKi.对输入e和ec,进行模糊化,根据模糊规则表,得到ΔKp和ΔKi的模糊量,在经过重心法进行解模糊,从而得到对应的ΔKp和ΔKi的数字量,从而根据式(2)进行PI 参数的调节.在考虑专家经验的基础上,结合实际的控制要求,设计对应的模糊规则见表1 及表2,从而根据模糊规则表得到49 条控制规则:IFeis NB andecis NB then ΔKpis PB and ΔKiis NB;IFeis NB andecis NM then ΔKpis PB and ΔKiis NB …. 表1 Kp 控制规律Tab.1 Kp control rule 表2 Ki 控制规律Tab.2 Ki control rule 为验证本文中模糊PI 控制器的控制效果,在Matlab/Simulink 中建立了全桥LLC 谐振电路模糊PI控制仿真模型.全谐振变换器主电路仿真参数见表3. 表3 主电路参数Tab.3 main circuit parameters 为比较模糊PI 与传统PI 控制之间的控制效果,本文在输入电压突变的条件下,分别仿真对比了两种控制方式的控制结果.仿真结果见图10.见图10(a)为传统PI 控制下,当输入电压由12 V 突变至24 V 时,输出电压波形;图10(b)为在模糊PI控制方法下,输入电压由12 V 突变到24 V 时变换器的输出电压波形. 从图10 中可以看出,采用模糊PI 控制方法系统具更好的动态性能.此外,调节时间、超调量等性能指标均优于传统PI 控制方式.在模糊PI 控制方式下,输出电压进过大约240 ms 进入稳态,而采用传统PI 控制时,则需要经过大约330 ms 输出电压才能进入稳态.可见采用模糊PI 控制方式,其控制效果明显优于传统PI 控制. 图10 传统数字PI 控制与模糊PI 控制下变换器输出电压波形Fig. 10 converter output voltage waveform under traditional digital PI control and fuzzy PI control 在实验室搭建的样机见图11,其相关的实验参数见表4.为解决全桥LLC 谐振电路电压增益失真的问题,通过采用LLC 与PSFB 的结合,分别对电路轻载和重载进行控制.图12 为电路重载下的驱动波形图,其中图12(a)为 LLC 谐振控制,图12(b)为PSFB 控制.图13 为全桥LLC 电路谐振网络的关键点波形.图13(a)中对比开关管驱动与DS波形可知电路实现ZVS;图13(b)、图13(c)中通过对比谐振电流ir与励磁电流im及谐振电容,谐振电容周期内充放电,当谐振电流ir等于励磁电流im时,次级二极管ZCS 关断.通过对实验波形的分析,基本与理论分析结果一致,电路的软开关功能得以实现. 图11 实验样机Fig. 11 experimental prototype 表4 实验样机的电路指标参数Tab.4 experimental parameters of prototype 图12 电路驱动波形Fig. 12 circuit drive waveform 图13 谐振网络、变压器绕组、二极管实验波形Fig. 13 experimental waveform of resonant network,transformer winding and diode 图14 传统数字PI 控制与模糊PI 控制系统动态实验波形Fig. 14 dynamic experimental waveform of traditional digital PI and fuzzy control system 图14 为模糊PI 控制与传统数字PI 控制下,全桥电路由重载切换到轻载的突变过程实验波形图,从波形图中可以发现,当负载发生变化时,此时全桥电路由LLC 谐振模式切换到PSFB 模式,此外,在模糊控制下电路的动态响应速度快,经过较短的调相时间即可使得输出电压稳定. 本文利用模糊控制与LLC、PSFB 方式进行控制的一种新型模糊混合型全桥LLC 谐振变换器.该变换器具备以下优点:电路在轻载时输出电压增益不失真;对电路进行混合控制时,调节速度快;能够实现电路在全负载范围内功率开关管ZV-ZCS;采用模糊PI 控制方式对变换器的电压外环进行控制,调节时间、超调量等系统性能指标均优于采用传统PI 控制方式.1.1 全桥LLC 工作状态分析
1.2 移相全桥拓扑分析


2 混合控制器设计

2.1 模糊PI 控制器设计
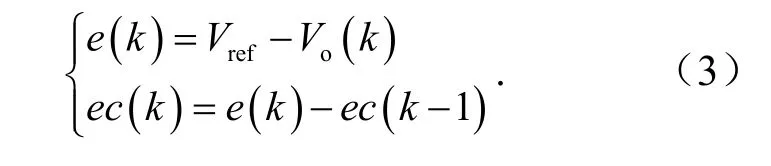

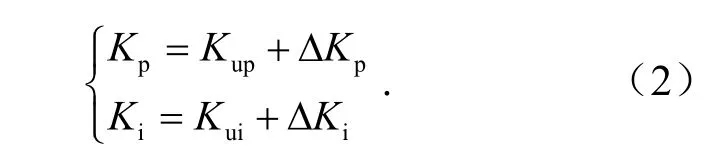
2.2 模糊隶属函数

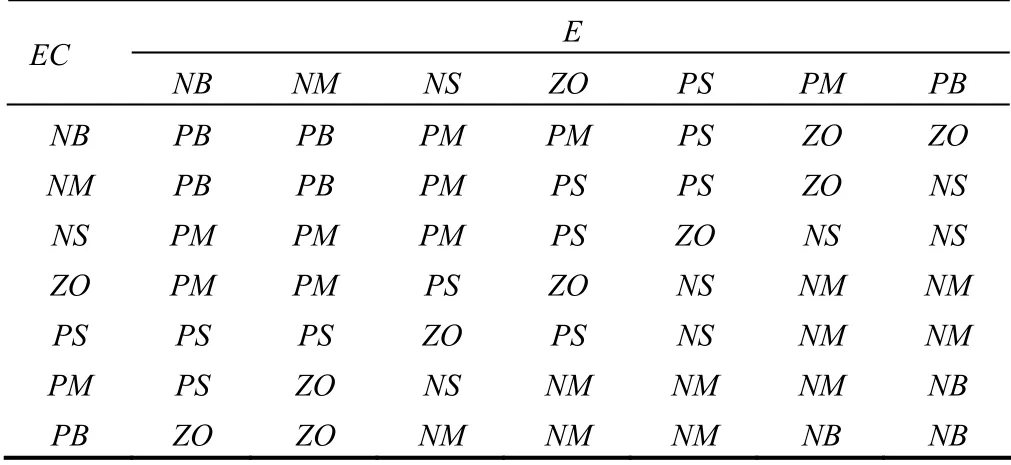
2.3 模糊规则及模糊推理

3 仿真结果与分析

4 实验结果与分析




5 结论

