六关节机械臂的轨迹规划
□ 张秀林
甘肃广播电视大学 兰州 730050
1 研究背景
目前,工业机器人的使用已非常普遍。但在实际应用中,机械臂在作业时会面临许多难题,如机械臂在启动和停止时手部出现严重抖动,机械臂末端到达指定位置不够精确等[1],如果情况比较严重,那么会引起机械臂机构严重受损[2]。机械臂的工作性能以工作效率和工作可靠性为衡量标准,所以当务之急是如何提高机械臂的工作效率及工作可靠性。
机械臂在沿轨迹运行过程中,要尽量避免角速度及角加速度突变,即运行轨迹曲线应尽量平滑连续,这样机械臂的运行就会比较平稳。但是在现实中,有时不能保证完全消除运动突变和抖动,机械臂在运行过程中构件的振动也无法完全避免,只能尽量减小。
为了能够提高机械臂的工作效率和工作可靠性,对机械臂的运动轨迹进行提前规划非常有必要。一般做法是,在对机械臂进行运行控制之前,提前规划好机械臂末端的运行轨迹,并采用仿真技术模拟试验,由模拟结果来分析机械臂的运行是否平稳,然后将预定轨迹信息输入控制系统,来控制机械臂的运行[3]。笔者对六关节机械臂进行轨迹规划。
2 轨迹规划概述
机械臂轨迹规划指在机械臂运动学和动力学的基础上,讨论在关节空间或笛卡儿空间中生产机械臂运动轨迹的方法,描述机械臂在多维空间中的运动路线,是运动学逆解的实际应用。在知道末端位姿的前提下,通过运动学逆解得到各个关节在相应时刻的转动量或平移量,合理规划出角位移曲线、角速度曲线、角加速度曲线,从而有效控制机械臂在运动过程中的冲击和振动,使机械臂的工作寿命得以延长。
机械臂运行轨迹端点既可以用关节坐标给定,也可以用笛卡儿坐标给定。笔者以六关节机械臂为研究对象,首先分析对比在关节空间和笛卡尔空间中进行机械臂轨迹规划的优缺点,选择合适的轨迹规划坐标空间;然后通过查阅大量文献资料总结分析多种轨迹规划插值函数,选定B样条插值计算进行六关节机械臂的轨迹规划;最后将得到的数据导入ADAMS软件,进行六关节机械臂轨迹规划仿真。
3 轨迹规划坐标空间
在关节空间中进行机械臂的轨迹规划,将关节变量表示为时间的函数,这一函数的一阶、二阶导数分别表示机械臂运行的速度和加速度,由此确定各关节的位置、速度、加速度随时间变化的规律,具有计算快、容易实现等优点,但机械臂末端的运动轨迹不直观[4]。总体而言,在关节空间进行轨迹规划有三方面优点:容易实现,直接用运动时间的受控变量规划运动轨迹,轨迹规划可接近实时运行进行,缺点是难以确定运动中各杆件的位置。
在笛卡尔空间中进行机械臂的轨迹规划,应用某种定义的函数来规划机械臂末端执行器的运动轨迹,将末端执行器位置、速度、加速度表示为时间的函数,其它各关节的位置、速度、加速度由末端执行器导出。通常通过运动学逆解得出关节位移,应用逆雅可比求出关节速度,应用逆雅可比及其导数求出关节加速度。在笛卡尔空间中进行规划轨迹,末端执行器的运动轨迹清晰、直观[5]。由于各关节的控制驱动是在关节空间中进行的,因此需要将笛卡尔空间约束转换至关节空间,而控制器所需要的关节参数通过大量运算得到,由此造成计算量较大。同时,计算结果也很难保证不存在奇异点,如所求轨迹在工作空间之外、关节变量值发生突变等。
由上述分析可见,在关节空间进行轨迹规划,不需要考虑笛卡尔空间中两个路径点之间的轨迹曲线,仅以关节变量表示为时间的函数来描述机械臂的轨迹,计算简单、容易。由于关节空间与笛卡尔空间并不是连续的对应关系,关节空间内不会产生机构奇异的现象,因此避免了在笛卡尔空间中规划时所出现的关节失控问题。综合分析后,笔者选用关节空间进行六关节机械臂的轨迹规划。
4 轨迹规划插值函数
在关节空间中进行机械臂轨迹规划时,需要给定起始点和终止点机械臂末端的位姿,对关节变量进行插值运算。采用逆运动学程序将各关节路径点转换为各关节矢量角度值,根据每个关节路径点拟合出一条光滑曲线,使轨迹从起始点开始,依次通过所有关节路径点,最后到达终止点,完成轨迹规划。对于每一段轨迹,各关节运动时间均相同,各关节函数之间相互独立,这样保证所有关节同时到达关节路径点和终止点,从而得到机械臂各关节应有的位置和姿态。
对关节路径点进行插值时,应满足一系列约束条件,各个关节的位移、速度、加速度在整个时间间隔内需满足连续性要求,其极值必须在各个关节变量允许范围之内。在约束条件下,可以选取不同类型的关节插值函数,生成不同的轨迹。
假设关节变量的时间函数采用多项式序列给定,某关节点轨迹应用P个多项式,要满足初始和终止条件,保证变量在多项式衔接处的连续性,就需要确定3(P+1)个参数。这种规划称为两点式轨迹规划。基本的两点式轨迹规划方法有三次多项式规划[6]、五次多项式规划[7]、带抛物线过滤的线性规划、过中间点的轨迹规划[8]等。
若额外给定附加的中间条件,如位置,则对于每个中间条件,需要增加一个参数,这种规划称为带中间点的两点式轨迹规划。通常,可以给定两个中间位置,一个靠近起始位置,另一个靠近终止位置。这样除了可以较好地控制运动外,还能够保证以适当的方向离开起始点和接近终止点。因此,对于连接初始位置和终止位置的每个关节变量,一个奇次多项式就足够了,或采用两段四次多项式轨迹加一段三次多项式轨迹[9]、两段三次轨迹加一段五次轨迹[10]、五段三次轨迹[11]、B样条曲线规划[12]。经过分析各种轨迹规划方法,进行对比,笔者采用B样条曲线进行六关节机械臂的轨迹规划。
5 关节空间B样条曲线轨迹规划
B样条函数定义式为:
(1)
式中:u为第i段内的增量参数;Bi,k(u)为第i段k次B样条基函数,k>1,i=1,2,…,k-1。
设机械臂在关节空间中有型值点P1、P2、…、Pm,由连续条件及边界条件可以求出m+2个控制点V0、V1、V2、…、Vm+1,每相邻两型值点之间用B样条曲线连接,整个轨迹由m-1段B样条曲线拼接而成。第i段B样条曲线连接Pi与Pi+1,第i段B样条曲线由Vi-1、Vi、Vi+1、Vi+2四个控制点控制,且控制点的坐标为Vi-1(vi-1,qi-1)、Vi(vi,qi)、Vi+1(vi+1,qi+1)、Vi+2(vi+2,qi+2),四阶三次均匀B样条曲线在第i段B样条曲线u处的矢量表达式θi(u)为:
θi(u)=X0(u)Vi-1+X1(u)Vi+X2(u)Vi+1
+X3(u)Vi+2
(2)
式中:Xi(u)为含有参数u的三次多项式。
根据连续性要求,相邻两段B样条曲线在连接处的矢量θi(u)、θi+1(u)应分别在u=0和u=1处满足条件:
θi(1)=θi+1(0)
(3)
同理,相邻两段B样条曲线在连接处的速度矢量、加速度矢量、加速度变化率矢量应分别在u=0和u=1处满足连续性条件。
此外,还必须满足柯西关系,即坐标变换后不变性条件:
X0(u)+X1(u)+X2(u)+X3(u)=1
(4)
由上述连续性条件和式(4),可以求出Xi(u)多项式为:
(5)
(6)
(7)
(8)
可得第i段B样条曲线u处矢量θi(u)为:
(9)
参数u取值为0~1之间,就可以得到第i段B样条曲线。但是,要对型值点进行轨迹规划,就必须先根据已知的型值点来求出控制点。P1,P2,…,Pm为关节空间的型值点,满足以下条件:
θi-1(1)=θi(0)=Pii=1,2,…,m-1
(10)
θi-1(1)=θi(0)=(Vi-1+4Vi+Vi+1)/6
(11)
式(10)、式(11)中有m+2个未知数,但实际只有m个方程,因此必须要有另外两个附加条件,即边界条件:
V1=V0
(12)
(13)
由式(13)可以确定唯一一组Vi值,由此可以确定三次B样条曲线。
在第i段B样条曲线上,任意取一个点,其横坐标vi(u)为:
(14)
在第i段B样条曲线上,任意取一个点,其纵坐标qi(u)为:
(15)
B样条曲线轨迹规划具有分段处理、计算速度较快、占用计算机内存较少等优点。
6 B样条插值仿真
以空间圆曲线为预设轨迹,空间圆方程为:
(16)
式中:(x,y,z)为空间圆路径点坐标;(x0,y0,z0)为空间圆圆心坐标;R为空间圆半径:θ为空间圆圆心至路径点连线与X轴正方向的夹角;α为空间圆圆心至路径点连线在YOZ平面上投影与Y轴正方向的夹角。
在空间圆上均匀取12个路径点,见表1。

表1 空间圆路径点坐标
在对六关节机械臂进行ADAMS软件仿真之前,基于逆运动学,应用MATLAB软件求解出到达表1中12个路径点所对应的六关节机械臂的各关节角度[13],见表2。
在ADAMS软件中进行仿真时,为六关节机械臂各个关节添加驱动函数。
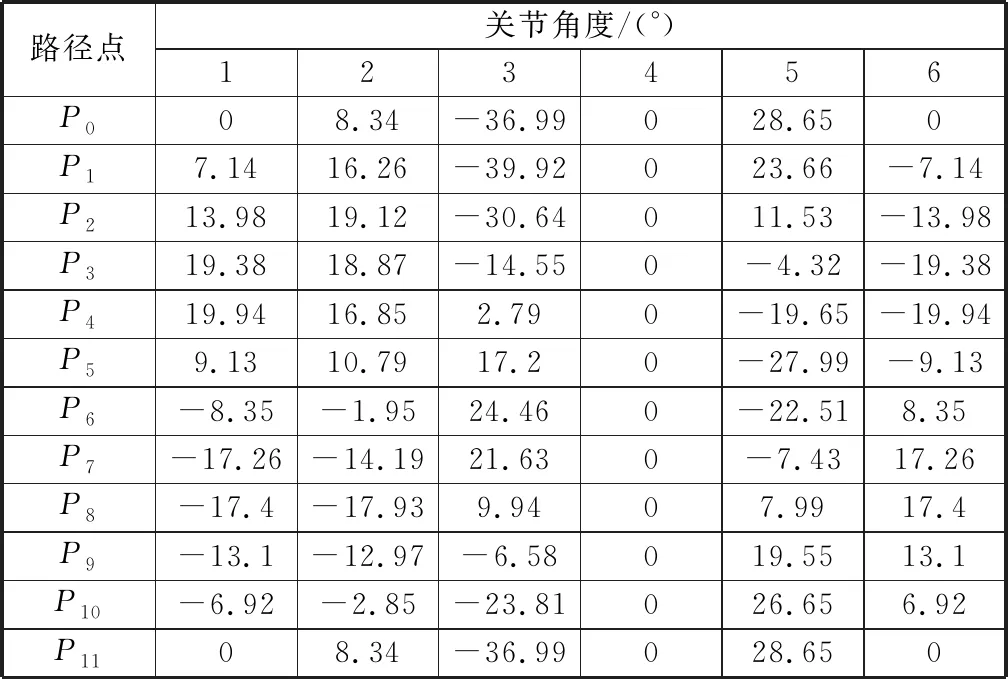
表2 空间圆路径点对应机械臂关节角度
仿真步数设为50步。在仿真过程中,可以看到六关节机械臂运动过程轨迹比较平稳。各关节的角位移、角速度、角加速度曲线依次如图1、图2、图3所示。

▲图1 六关节机械臂各关节角位移曲线
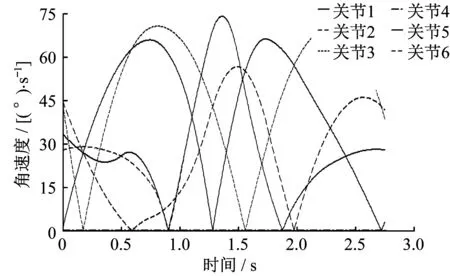
▲图2 六关节机械臂各关节角速度曲线
由图1、图2、图3可以看出,各关节的角位移曲线平滑,角速度曲线变化平顺,但是角加速度曲线有突变点,说明六关节机械臂末端执行器在工作过程中存在振动现象,因此,对六关节机械臂还需要进一步进行优化。
7 结束语
笔者以六关节机械臂为研究对象,在关节空间采用B样条曲线进行轨迹规划。在轨迹规则中,对关节空间和笛卡尔空间进行转换,在笛卡尔坐标系下插补获得轨迹上的型值点,然后采用逆运动学将这些型值点转换至关节空间中的各关节角度,再应用B样条曲线拟合得到各关节的运动轨迹。将得到的数据导入ADAMS软件进行仿真,得到六关节机械臂各关节角位移、角速度、角加速度变化曲线,结果显示各关节的角速度变化平缓,角加速度曲线有明显突变点,因此,对六关节机械臂还需要进一步优化。
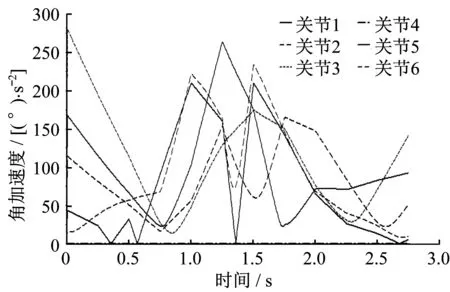
▲图3 六关节机械臂各关节角加速度曲线

