超深圆形基坑施工期监测数据分析与研究
朱 渊,谭 勇,秦 朋,田亚玲,刘 源
(1、长江科学院工程安全与灾害防治研究所 武汉430010;2、长江科学院水利部水工程安全与病害防治工程技术研究中心 武汉430010;3、长江科学院国家大坝安全工程技术研究中心 武汉430010)
0 引言
基坑工程的变形受到工程地质、水文地质条件及外荷载等诸多因素的影响[1],使得支护结构型式多种多样。随着深大基坑工程的不断涌现,传统的支撑方式已无法满足支护要求,因此圆环内支撑应运而生[2]。
圆形深基坑采用地下连续墙作为围护结构,逆作法施工内衬综合考虑圆形支护结构具有较好的受力性能和稳定性,充分发挥混凝土的抗压性能[3-7],利用圆形结构自身的拱效应提供支撑,可以避免大面积设置支撑梁,减少拆撑工况,提高土方开挖效率[8]。本文通过某超大圆形深基坑监测数据进行分析研究,并结合理论计算分析,总结复杂地质条件下基坑的变形形状及周边环境的变化,得出一些有价值的结论,可为类似工程提供经验和借鉴。
1 工程概况
某地下输水工程采用深埋隧洞方式,在地下平均40~60 m 空间建设输水隧洞,其中某圆形工作井竖井外径为35.9 m,基坑底部高程-54.50 m,地面平整高程3.30 m,开挖深度57.80 m,采用地下连续墙+混凝土内衬支护方式,地下连续墙厚1.2 m,嵌入井底,逆作法内衬墙厚1.2~1.5 m。根据设计原则及相关规范标准,确定基坑围护结构侧壁安全等级为一级,结构重要性系数为1.1。
工作井井身上部为人工填土和冲积层,厚度8.6~23.4 m,主要有:①人工填土层、②3淤质细砂层、②4淤质黏土层;其下为花岗岩,其中全风化上段厚11.2~32.3 m,可塑~硬塑,全风化下段厚17.3~24.9 m,硬塑~坚硬土状。井底主要位于全风化带,局部(工作井东部)为强风化带。井壁冲击层及全风化土自稳能力较差,砂层为含水层,强透水性,工程地质条件较差,井底全风化花岗岩黏性较差,泡水易软化,在施工过程中应加强井底排水措施并及时进行封闭处理。基坑主要物理力学参数如表1所示。
4 监测结果及分析

表1 主要物理力学参数Tab.1 Main Physical and Mechanical Parameters
4.1 连续墙钢筋应力
2 监测内容
基坑监测内容主要包括连续墙深层水平位移、连续墙顶部水平位移、连续墙顶部竖向位移、基坑周边地表沉降和位移、地下水位、连续墙钢筋应力、内衬墙钢筋应力及土压力。基坑监测点平面布置如图1所示。
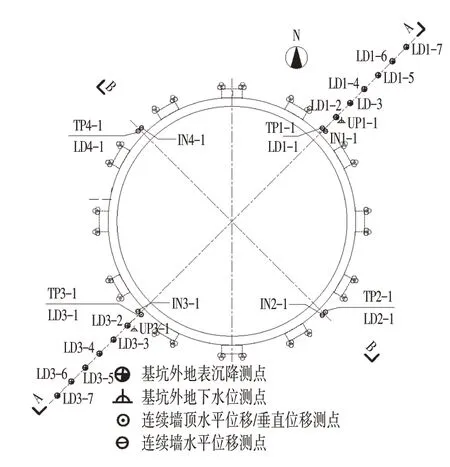
图1 基坑监测点平面布置Fig.1 Layout Plan of Foundation Pit Monitoring Points
3 施工及支护方案
基坑采用地下连续墙+内衬墙的支护方式,不加设支撑,利用圆形支护自身的拱效应来提供支撑。地下连续墙既要承受水土的水平荷载,又要承受竖向荷载,同时起防渗的作用,即“两合一”墙。环形地下连续墙共24 个槽段,分2 期浇筑,相邻槽段采用高压旋喷桩进行防渗加固处理。内衬墙1~5层厚度为1.2 m,底面斜坡1∶4,6 层以下厚度为1.5 m,底面斜坡1∶5。内衬墙采用逆作法施工,土方分11 层开挖,基坑边开挖边施工内衬,开挖至-50.5 m 底高程后浇筑底板。每层开挖顺序从四周向中间进行,根据时空效应施工方法分层分块开挖,开挖到内衬、环梁作业面后,及时进行内衬、环梁的施工,尽量减少基坑无支护的暴露时间,严格控制基坑侧向变形。对于内衬、环梁采用局部开槽方法浇筑混凝土。
钢筋计布置在15#槽段和21#槽段2 个监测断面,每个断面布设4个钢筋应力监测点,具体结果如图2 所示。鉴于篇幅限制,选取15#槽段应力监测点进行分析,其中正值表示受拉,负值表示受压。
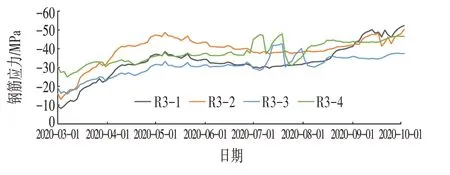
图2 钢筋应力变化曲线Fig.2 Rebar Stress Curve
由图2 可以看出,钢筋应力随基坑开挖发生了显著的变化,具体如下:
⑴在基坑开挖前期,随基坑开挖深度增加,钢筋应力总体呈不断增大的趋势,局部存在一定程度的波动,其波动原因可能是受到土方开挖及机械设备扰动等影响。基坑开挖中后期,钢筋应力变化幅度较小,且逐渐减小,其主要原因在于基坑开挖前期阶段,内衬墙达到强度需要一段时间,无法及时发挥作用,使得连续墙承担了大部分受力,开挖后期阶段,内衬墙已发挥作用,分担了一部分荷载,使得连续墙钢筋应力减小。
⑵基坑开挖至第8 层,由于基坑开挖深度增大,在内衬墙施工之前,开挖面附近测点R3-3、R3-4钢筋应力明显增大,但均在设计允许范围内。内衬施工完毕,钢筋应力则明显降低。
⑶8月20日~9月27日,最后一层土方(第11层,开挖深度10 m)开挖深度大,内衬墙施工时间较长,钢筋应力明显增大。
钢筋主要承受压力,但所受压力不大,由于受施工、周边堆载及机械振动等影响,钢筋应力出现波动,圆形内衬结构对基坑内力及变形具有重要作用。
4.2 地下连续墙深层水平位移
基坑地梁墙布置了4 个测斜测点,IN1-1(3#槽段)、IN2-1(9#槽段)、IN3-1(15#槽段)、IN4-1(21#槽段)。连续墙深层水平位移如图3所示,位移向基坑内为正,向基坑外为负。
基坑前5 层土方开挖时,连续墙侧向变形较小。由图3可看出,连续墙水平位移呈现“中间大,两头小”的特征,空间效应明显。连续墙水平位移随基坑开挖深度增加而逐渐增大,最大位移出现的位置也随基坑开挖深度增大而逐渐下移,水平位移越大,水平位移最大位置在基坑开挖面以下1~5 m 处。连续墙水平位移主要发生在深层土体开挖阶段。

图3 测点深层水平位移-深度关系曲线Fig.3 Measuring Point Horizontal Displacement-depth Relationship Curve
由于土方开挖速度过快,地连墙无法均匀受压,测斜管IN1-1、IN4-1 中上部发生朝向基坑外侧变形,最大值分别达到13.21 mm、12.98 mm。基坑开挖至底板标高(-50.9 m),测斜管IN1-1、IN2-1、IN3-1、IN4-1朝向基坑内侧最大水平位移分别为3.62 mm、7.12 mm、13.18 mm、5.45 mm,连续墙最大水平位移与开挖深度之比为0.026%,远小于常规基坑的相对侧移[9]。表明圆形支护结构拱效应作用能很好抵抗基坑变形,维持基坑的稳定性。
图4 为第9 层土方开挖至设计标高(-36.4 m)连续墙水平位移随时间变化过程线。由图4 可以看出,土方开挖过程中,暴露的连续墙通过向基坑内变形来重新达到应力平衡。由位移变化趋势可知,连续墙变形主要发生在土方开挖阶段,由于连续墙刚度较大,后期变化量很小,内衬墙施工完成后,变形部分回弹。
4.3 连续墙顶部水平位移
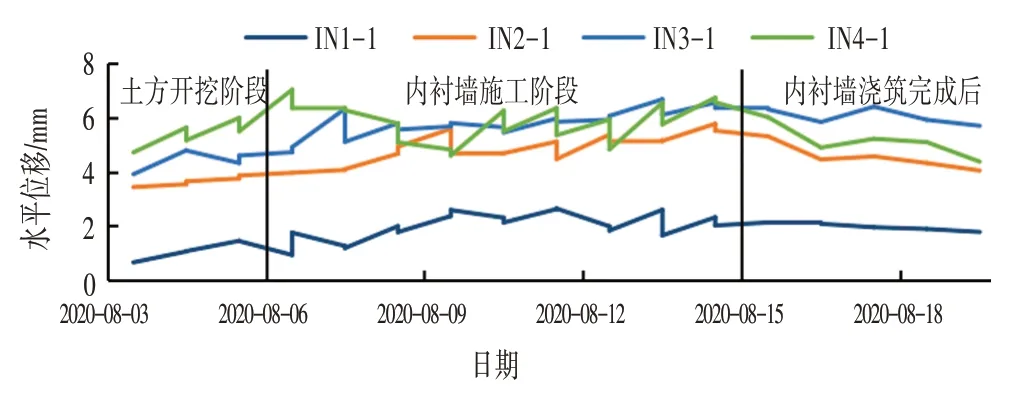
图4 第9层土方开挖至设计标高(-36.4 m)连续墙水平位移-时间关系曲线Fig.4 The Horizontal Displacement-time Curve of the Continuous Wall from Excavation of the 9th Layer to the Design Elevation(-36.4 m)
连续墙顶部水平位移如图5、图6所示(负值表示向外侧移动),图5、图6中为各测点墙顶的相对位置。基坑开挖过程中,测点TP1-1、TP2-1主要发生向基坑外侧变形,TP1-1测点向基坑外侧变形最大,为4.07 mm。测点TP3-1、TP4-1 主要发生向基坑内侧变形,TP3-1测点向基坑内侧变形最大,为5.35 mm。可以发现,连续墙顶部水平位移均较小,波动较大,无明显变化规律,主要是由于连续墙自身具有较大刚度,抵抗变形能力强。基坑开挖至第10 层底部标高以后,连续墙顶部水平位移量明显减小。
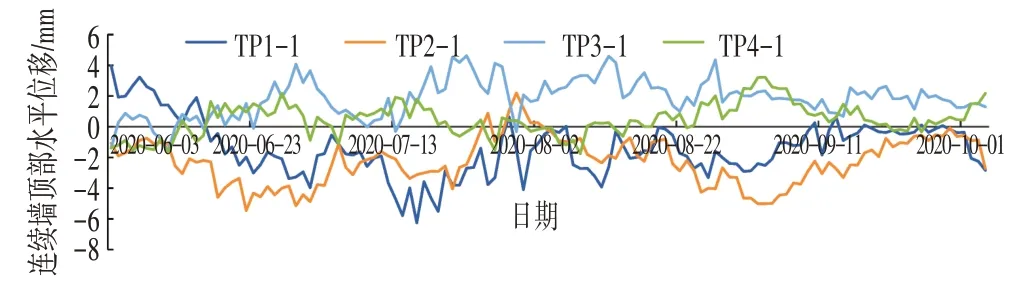
图5 连续墙顶部水平位移-时间关系Fig.5 Horizontal Displacement of the Top of the Continuous Wall-time Relationship

图6 连续墙顶部水平位移测点变化关系Fig.6 The Relationship of the Horizontal Displacement Measurement Points on the top of the Continuous Wall
4.4 地下连续墙垂直位移
连续墙顶部共布置4 个垂直位移测点,各测点位移随时间变化的曲线如图7 所示(负值表现为上抬)。由图7可知,基坑开挖前期,连续墙顶部垂直位移变化量较小,但有一定程度的波动。2020 年8 月20 日,基坑开挖至第10层,由于挖土较深,土方卸荷较大,施工工期较长,连续墙顶部沉降量迅速增加,测点LD4-1沉降量最大,达到17.29 mm,已超出设计报警值16 mm。底板浇筑完成一段时间内,连续墙顶部沉降量继续增大,一段时间后,沉降量趋于稳定。
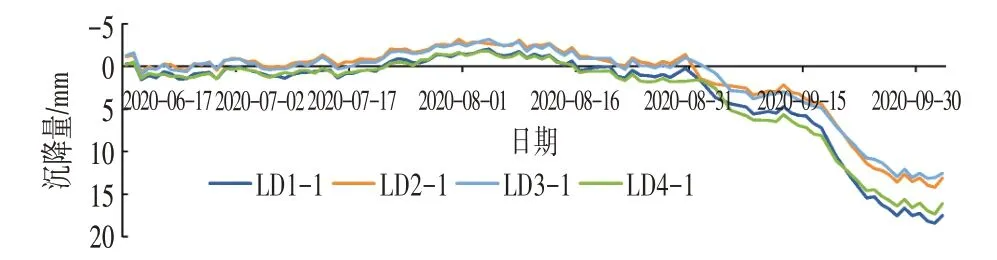
图7 连续墙顶部垂直位移-时间关系曲线Fig.7 Vertical Displacement on Top of Continuous Wall-Time Relationship Curve
5 支护结构变形与位移计算
5.1 计算方法
圆形支护结构内力及位移的计算方法有很多,文献[1]详细介绍了各种计算方法,文献[10]提出圆形基坑可充分发挥围护结构和土的拱效应。本工程基坑支护结构为“二合一”形式的无内支撑的地下连续墙,本文采用“竖向平面弹性地基梁”法计算围护结构的位移及内力,将圆形基坑看作弹性地基梁,把圆形支护的拱效应等效为由一定刚度的水平支撑,这种支撑在深度方向上分布是连续的,使围护结构具有相同的侧向刚度。将三维空间问题简化为平面问题进行计算。
被动侧土压力简化为弹簧支撑,在弹性地基单元每一节点处设一附加弹簧支撑,其刚度Ks为:

式中:u 为圆环的径向位移;E1为支撑的弹性模量;P 为作用在支撑两端的力;L 为支撑的长度;A 为支撑截面积。
由弹性力学平面应变问题推导出拱效应的等效支撑弹性模量E1为:

式中:E 为圆形支护的弹性模量;ν 为泊松比;r 为半径;a、b为圆环的内外径。
5.2 理论计算
计算支护结构内力及位移不考虑内衬的影响,取最不利情况。计算等效支撑弹性模量时,参考逆作法施工,在开挖深度以上每2 m 等效为1 道支撑,支撑宽度2 m。圆形支护结构弹性模量E=30 GPa,取ν=0.2。由式⑶计算得到E1=0.05 GPa。用弹性地基梁法计算时支撑安装过程如表2所示,计算简图如图8所示,基坑开挖到第7、8 层时的计算结果与实测结果对比如图9所示。
按上述方法运用有限元软件进行计算,将2 个工况的理论计算值与实测值进行对比,如图9 所示。连续墙上部发生向基坑外侧变形,与计算值存在一定差异。分析如下:
⑴由图9可知,理论计算值与实测值变形趋势一致,水平位移随开挖深度增加而增大,最大位移位置在开挖面附近。每一工况下计算值比实测值偏大,这是因为理论计算等效支撑是在每层土方开挖后施加,而实际工程中拱效应一直存在,这也说明圆形支护结构的拱效应可以有效控制连续墙的水平变形。
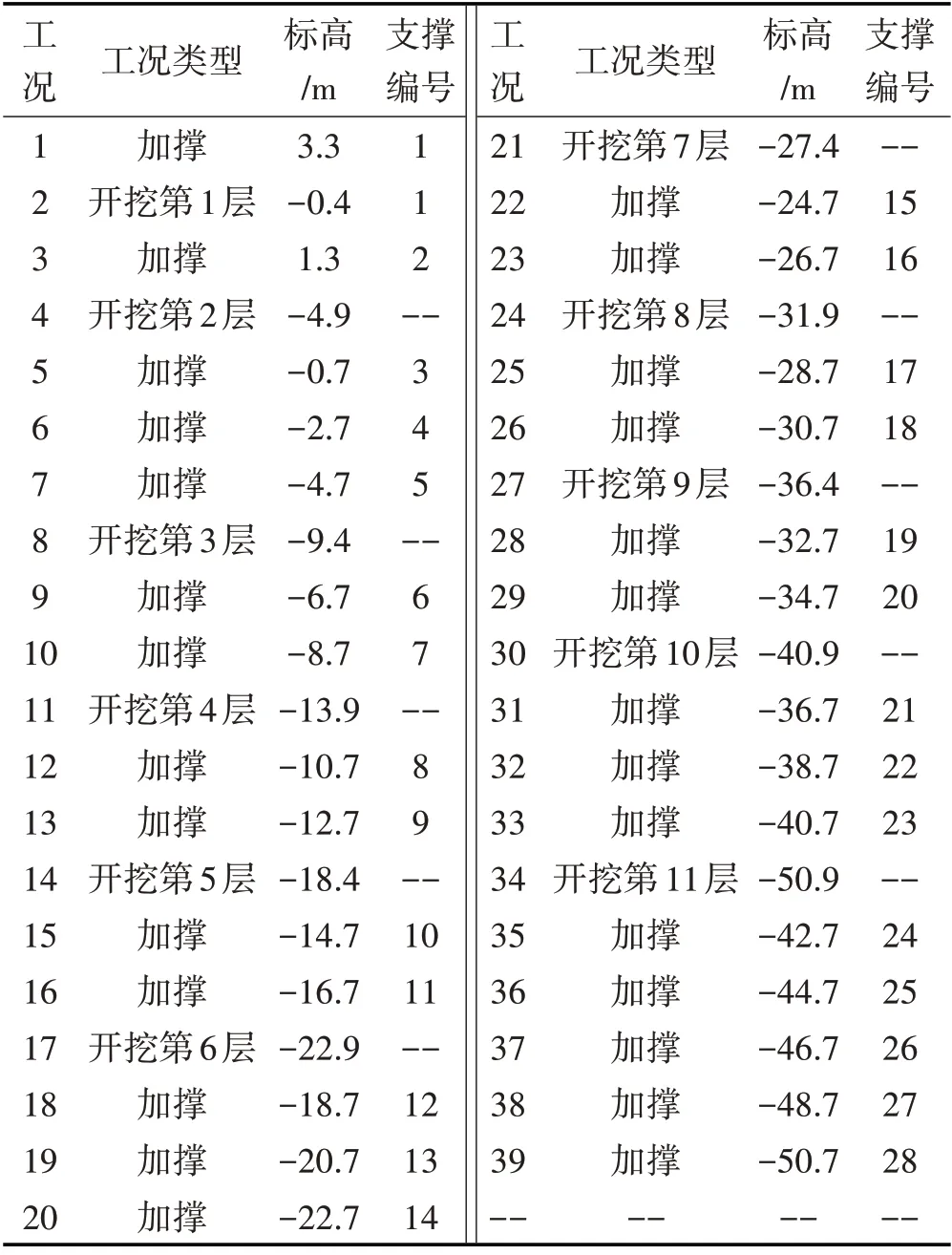
表2 支撑安装过程及工况Tab.2 Support Installation Process and Working Conditions
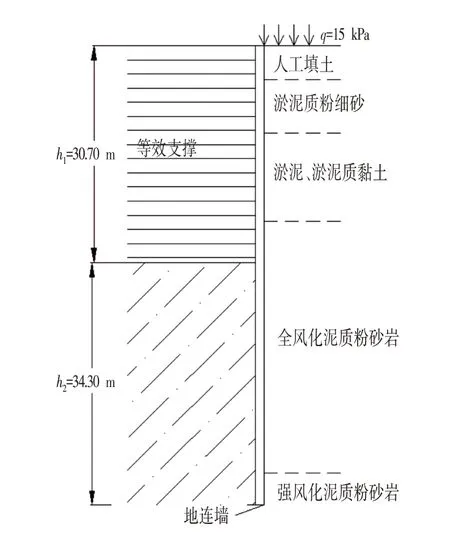
图8 计算简图Fig.8 Calculation Diagram
⑵连续墙上部变形理论计算值与实测值存在一定差异,这是因为施工阶段受地面超载及开挖速度的影响,对连续墙上部变形产生影响。
⑶不同工况理论计算值与实测值的吻合程度不同,开挖深度越大,连续墙变形拟合程度越好。
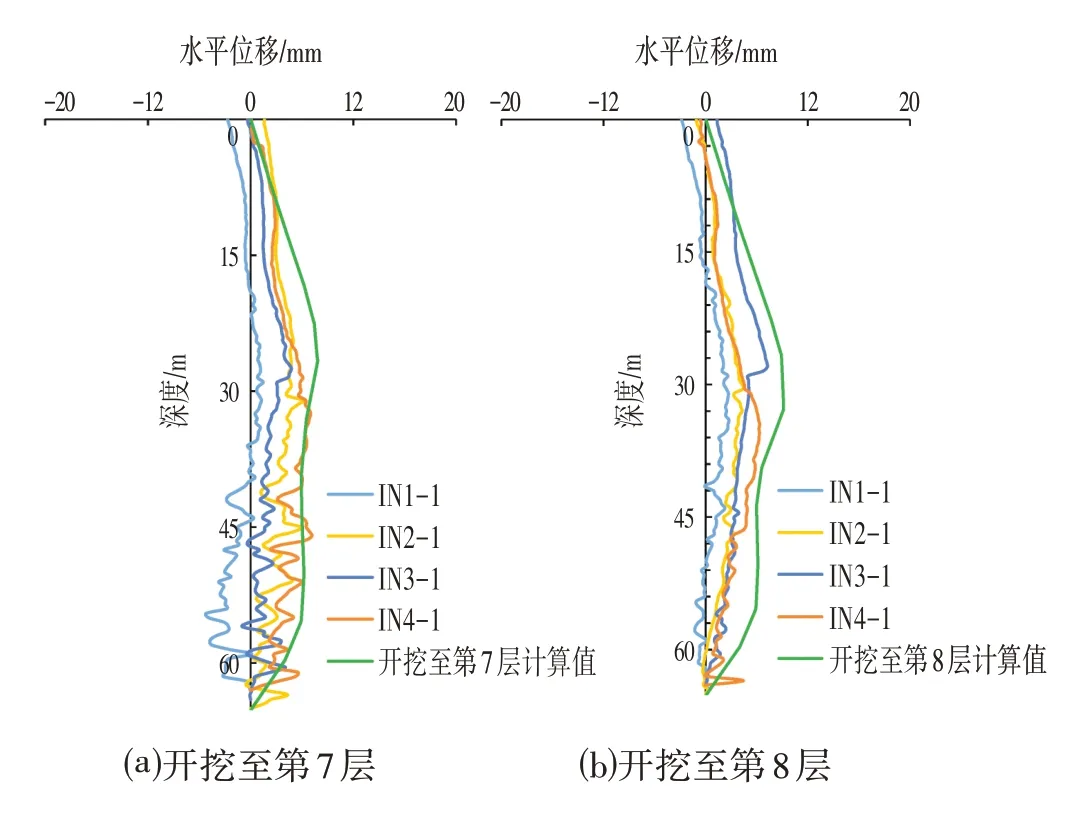
图9 理论计算和实际位移值对比Fig.9 Comparison of Theoretical Calculation and Actual Displacement Value
6 结论
⑴开挖卸荷引起的基坑围护结构变形主要发生在深层土体开挖期间,及时完成内衬墙施工可减小连续墙的水平位移。
⑵地下连续墙的水平位移随着基坑开挖深度的增加,水平位移最大值不断下移,且最大值在开挖层附近。施工过程中严格控制每层土体开挖后无内衬支撑时间,及时浇筑内衬墙,可以较好地控制基坑变形。该基坑地质条件较差,开挖深度大,但地下连续墙的变形较小,表明采用地下连续墙+内衬的支护形式能够较好地控制基坑变形。
⑶圆形围护结构抵抗变形的能力强,拱效应作用下围护结构变形较小。
⑷理论计算值与实测值吻合程度较好,但由于影响围护结构变形因素的复杂性及实际施工过程中一些不确定因素,使理论计算值与实测值存在一定的差异。

