厚壁蝶型弹簧用于基桩高应变测试的初步研究

徐长琦

（广东省建筑科学研究院集团股份有限公司 广州510500）

0 引言

高应变动力试桩法，是指所有能使桩土间产生永久变形（或较大动位移）的动力检测基桩承载力的方法［1］，该方法适用于检测桩的竖向抗压承载力和桩身完整性，相对于单桩竖向抗压静载试验而言，该方法费用较低、耗时较短、对场地要求较低，因此该方法在珠三角地区应用广泛。

高应变法结果对测试过程中传感器采集的力和速度曲线依赖性较高，《建筑基桩检测技术规范：JGJ 106—2014》及《建筑地基基础检测规范（广东省标准）：DBJ/T 15-60—2019》规定传感器安装处混凝土开裂或出现严重塑性变形导致力曲线明显未归零时不得提供承载力检测结果，避免了因混凝土非线性造成的力信号失真。混凝土受压时，理论上讲是对实测力值的放大，是不安全的，因此研究了一种通过将蝶型弹簧放置在桩顶以替代打击作用，从而进行力值测试的方案。

蝶型弹簧具有承载力高、刚度适宜、性能稳定等优点，可提供良好的竖向隔震效果，且碟片间存在锥面摩擦及边缘摩擦，往复荷载作用下可提供一定的阻尼耗散能量，因此在汽车、机械等领域应用广泛，亦常用于建筑结构的竖向隔震装置。

1 高应变测试力信号失真介绍

高应变测试通常采用环型应变式力传感器来检测高应变动力试桩中的桩身截面受力，传感器通过打入混凝土的膨胀螺栓紧贴着桩身进行安装，测量的是桩身77 mm（传感器标距）段的应变值，换算成力还要乘以桩身材料的弹性模量E，因此力不是它的直接测试量，而需通过下式进行换算：

由式⑴可知力值的大小与应变测量结果呈线性关系，因此力值测试是否准确，较高程度上依赖于传感器安装处混凝土的应变测试结果。

1.1 顺德某工程力信号失真案例

佛山市顺德区某人行天桥建设工程桩径为1.2 m，桩长31.5 m，入微风化岩，承载力特征值为2 600 kN，本次测试选择8 t重锤，落距1.2 m左右，采用欧美大地PDA（8G）高应变分析仪进行测试，传感器均通过仪器系统自带的校准方法进行校准，最终所得实测信号如图1所示，力值信号与速度信号严重不匹配，最大力值甚至达到16 596 kN，远超过8 t锤所能在1.2 m 的落距下产生的最大冲击力。通过观察传感器安装处混凝土外露面，发现轻微竖向裂缝，由此可知传感器安装处混凝土产生的严重塑性变形造成了力值信号失真。

1.2 混凝土塑性变形特性

图1 顺德某工程高应变实测信号Fig.1 Measured Signal of High Strain of a Project in Shunde

混凝土结构因其所遭受荷载性质的变化，结构响应存在很大差异，混凝土属于速率敏感性材料，应变率的变化会使结构的极限荷载、变形能力及破坏形式等发生重大变化，因此在研究混凝土结构的作用荷载时，有必要考虑荷载引起的应变率变化对荷载作用效果的影响［2］。

丛昕彧［3］通过对碱激发混凝土及其受弯构件静力与抗冲击性能研究发现，混凝土单点静力加载试验梁的破坏发展过程可被划分为3个阶段：线性发展阶段、强化阶段、破坏阶段。并借助重力式落锤冲击系统对混凝土落锤进行试验（见图2），试验混凝土梁在第1次落锤冲击下均产生少量细小裂缝，第2次冲击后，试验梁的裂缝数量增多，且缘由裂缝宽度增大，试验梁上表面混凝土在第2 次冲击后出现水平裂缝甚至碎裂。这一现象与高应变检测过程中混凝土桩帽开裂甚至破碎的现象一致（见图3、图4）。由此可知，由于混凝土非线性特征的存在，导致高应变检测过程中力值的测试存在较大的误差。谢和平等人［4］完成了应变率由10-5/s ～102/s 8个数量级范围内的混凝土受压试验，当应变超过一定数值时，峰值应力会出现明显降低的现象。

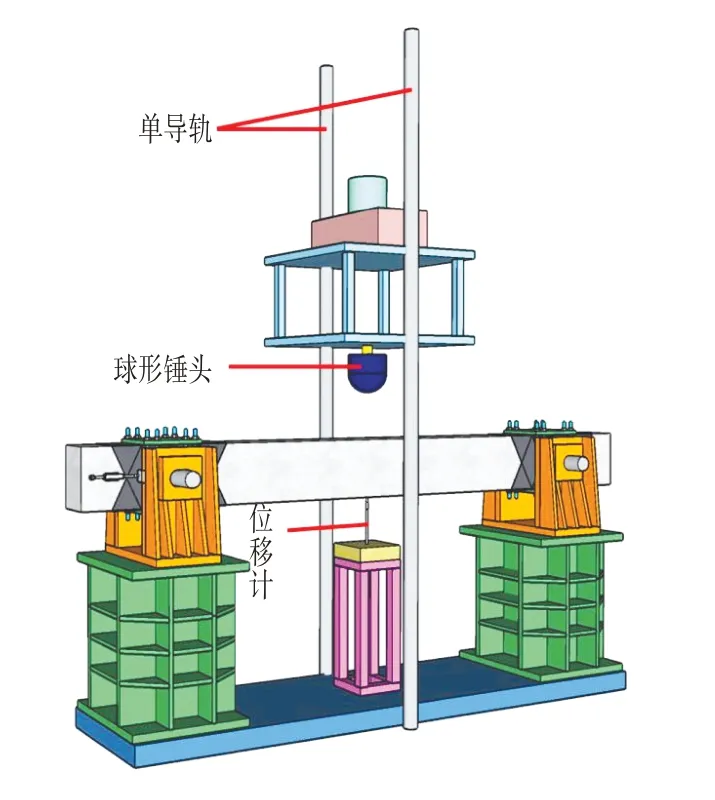
图2 落锤试验加载装置Fig.2 Loading Device of Drop Weight Test

图3 某高应变工地桩帽竖向裂缝Fig.3 Vertical Crack of Pile in a High Strain Construction Site

图4 某高应变工地桩帽破碎Fig.4 Breakage of Pile in a High Strain Construction Site

2 碟簧国家标准公式计算

本次试验研究选择大尺寸非常用厚壁碟簧（参照文献［5］表B.1 续），蝶型弹簧具有承载力高、刚度适宜、性能稳定等优点，试验蝶型弹簧参数如下：外径为500 mm，内径为253 mm，厚度为27 mm，最大变形量为8.25 mm，自由高度38 mm，弹性模量E=206 000 N/mm2，泊松比μ=0.3。

文献［5］规定单片碟簧承受的负荷F 与位移的关系可以表示成：

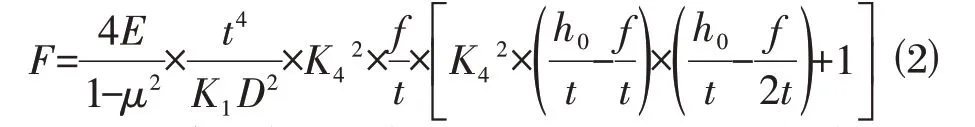
因此将文献［5］附录C 中C.1～C.15公式采用Matlab软件编辑成如图5所示M 文件，该程序文件在本次使用前已通过文献［5］中图C.2 中的计算和实测数据进行了对比验算，计算结果可靠。

将试验蝶型弹簧参数输入到该计算程序中易得：单片碟簧的负荷F=1.065 4×106N，大于文献［5］表B.1续中给定的荷载F=875 297 N（下文计算采用该给定的荷载），可知文献［5］给定的荷载考虑了一定的安全系数，偏安全。

图5 碟簧负荷计算程序Fig.5 Calculation Program of Disc Spring Load

3 有限元分析计算

3.1 模型建立

采用ABAQUS 软件进行分析计算，建立碟簧、上压板、下承台板的分析模型，各部件示意图如图6、图7所示，本次计算分析均采用毫米制单位：毫米（mm）、吨（ton）、牛（N）、秒（s）、兆帕（MPa）。

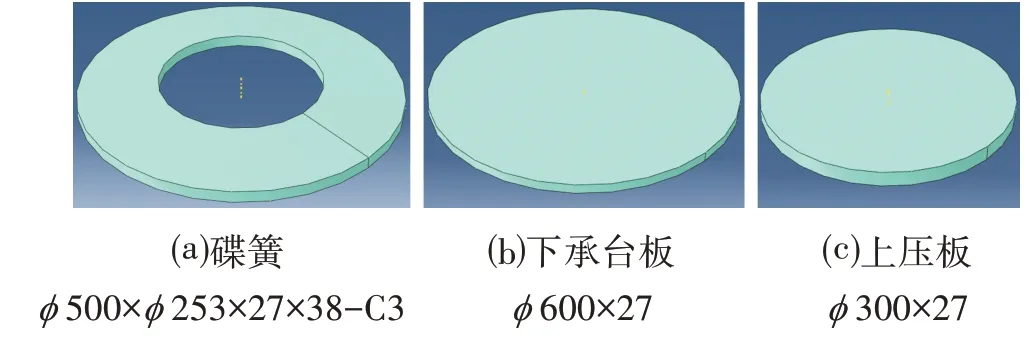
图6 部件示意图Fig.6 Component Diagram

图7 部件组装及网格划分示意图Fig.7 Schematic of Component Assembly and Meshing

3.2 外荷载添加

在上压板的中心位置分级施加竖向集中荷载，荷载分级为5级，加载情况如表1所示。

3.3 相互作用关系

不同约束条件对计算结果影响较大，为此合理选择相互作用关系类别较为重要。考虑到单片碟簧在试验机上加载的过程中上、下端的压板材质一致，因此将碟簧顶部、底部分别与上、下端板的约束条件设置相同。本文经过多次试算，考虑碟簧的变形特征，将碟簧底部与下承台板顶面设置接触面，该接触面切向属性（Tangential Behavior）为罚函数摩擦类别（Penalty），摩擦系数为0.9，允许弹性滑动；法向属性（Normal Behavior）为硬接触（“Hard”contact）［6-7］。

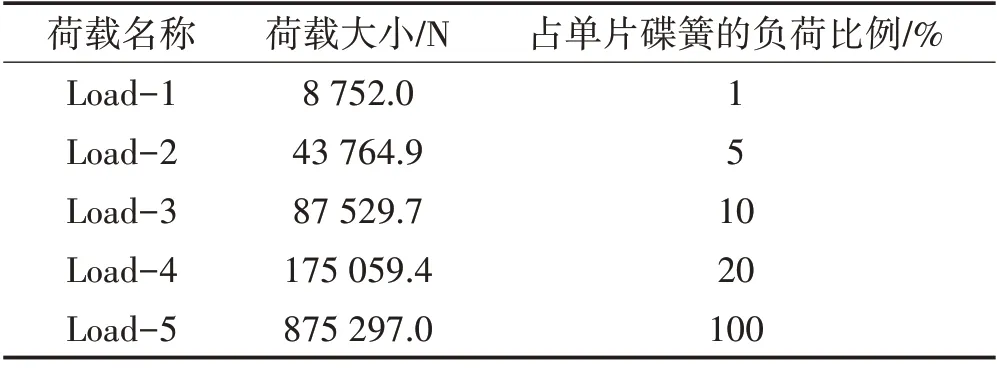
表1 外荷载分级加载Tab.1 External Load Classification

3.4 边界条件

仅限制下承台板的底面的竖向位移。

3.5 材料弹塑性

按照研究学者做的60Si2MnA 钢拉伸性能试验研究［8-9］，材料应力在2 000 MPa范围内，可不考虑塑性变形。经过初步试算，碟簧在本次荷载试验中的最大主应力在1 643 MPa 左右，见图8⒞的最大值和图9，可知，碟簧在本次试验负荷下材料均处于弹性变形范围内，因此不需要考虑塑性变形。

4 计算结果

4.1 竖向变形U3（见图10、表2）

4.2 OM点计算应力（见图8、图11、图12）

由图10 可知，在外荷载F=875 297 N 作用下，碟簧的竖向变形量仅为10.36 mm左右，可见碟簧的刚度较大，能够承受较大的荷载，最大主应力出现在碟簧底部，达到1 643 MPa左右（见图9），OM点的最大应力为239.7 MPa左右，仍处于塑性变形范围内。

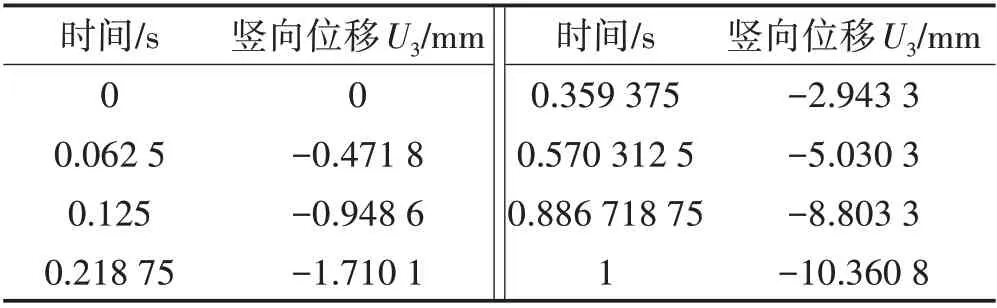
表2 外荷载分级加载Tab.2 External Load Classification

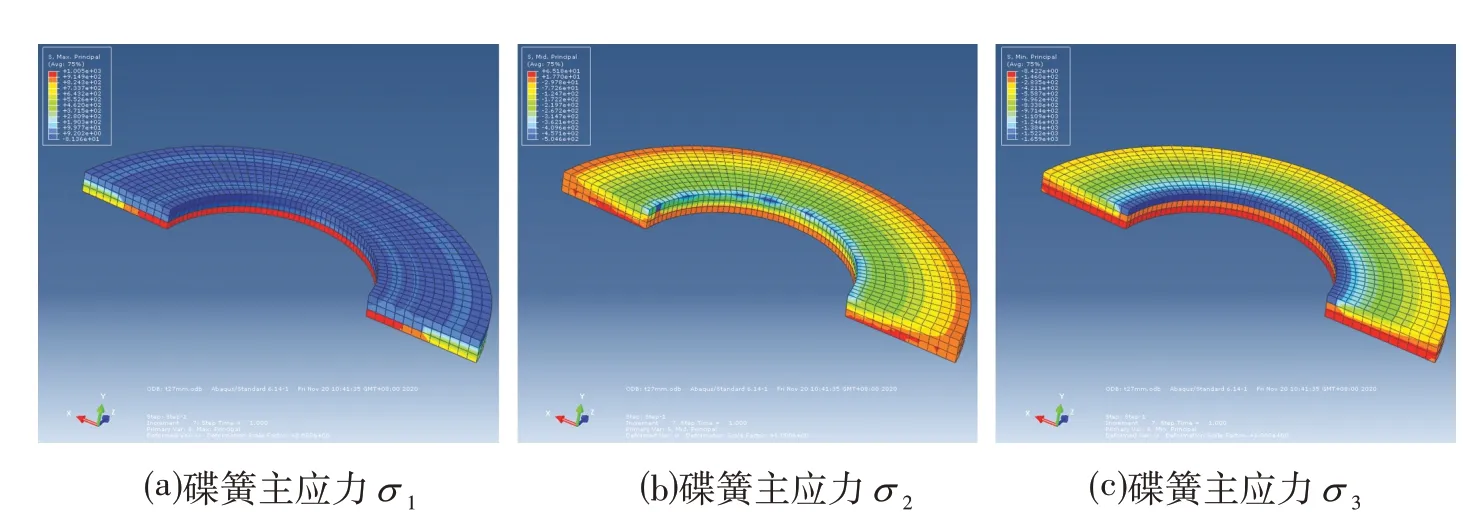
图8 荷载作用结束时刻碟簧的应力云图Fig.8 Stress Nephogram of Disc Spring at the End of Load

图9 荷载作用下碟簧内缘上、中、下的最值主应力时程曲线（2 123单元即为碟簧规程中OM点所在单元）Fig.9 Time History Curve of Maximum Principal Stress at Upper，Middle and Lower Inner Edge of Disc Spring under Load（Unit 2 123 is the Unit of OM Point in Disc Spring Specification）

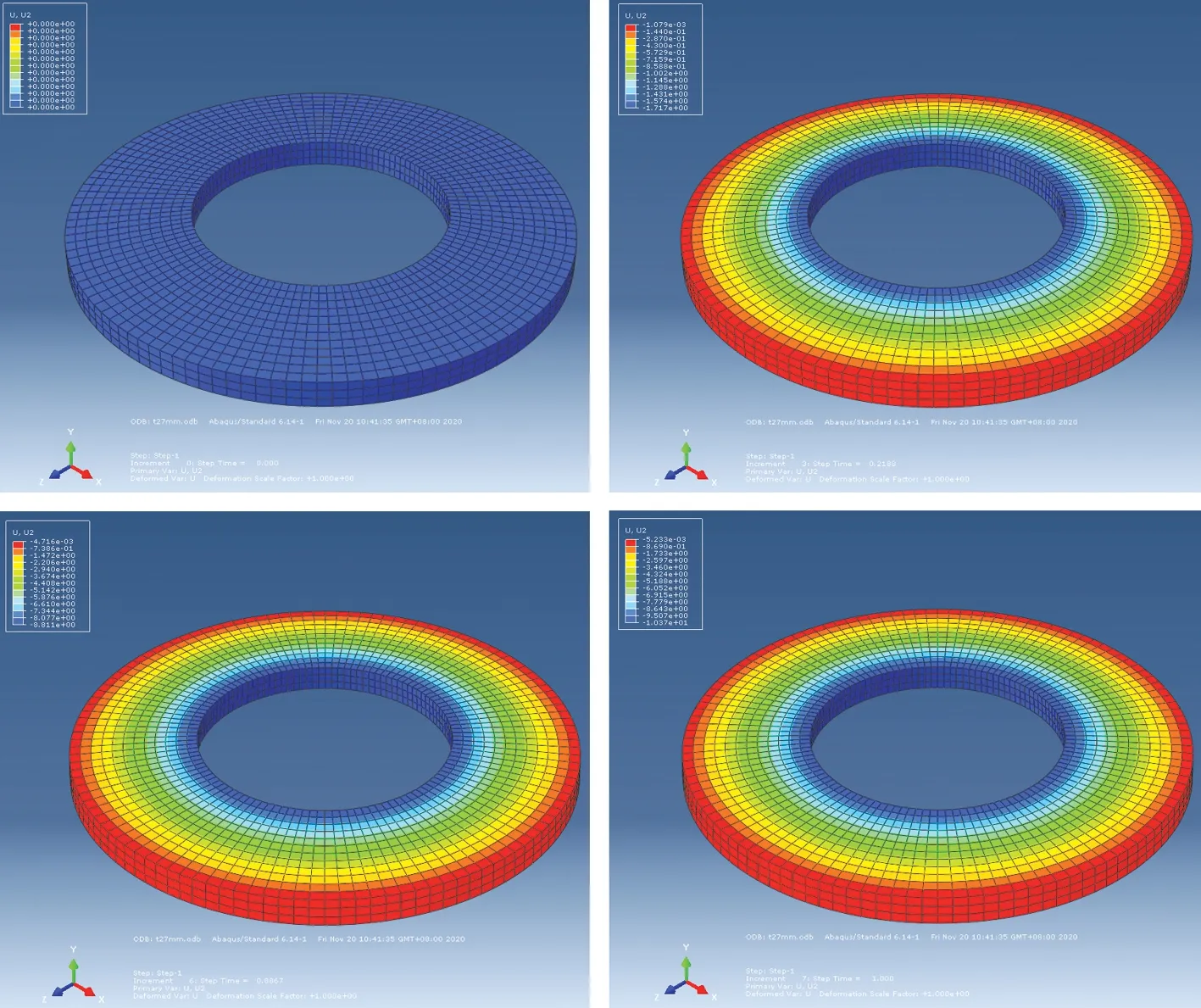
图10 不同时刻碟簧竖向变形云图（荷载作用时刻依次为：0 s、0.218 75 s、0.886 7 s、1 s）Fig.10 Cloud Chart of Vertical Deformation of Disc Spring at Different Times（the Loading Time is 0 s，0.218 75 s，0.886 7 s and 1 s Respectively）

5 结论

本文对厚壁蝶型弹簧进行了受力分析，通过分析可知，厚壁蝶型弹簧刚度较大，能够承受较大的荷载。同时由于60Si2MnA 钢材料力学性能良好，在受力过程中始终保持在弹性变形范围内，无塑性变形发生，变形可恢复。因此选取厚壁蝶型弹簧放置于桩顶作为高应变替打器，通过测试蝶型弹簧的变形来计算冲击碰撞过程中的应力具备可行性，该方法可以有效避免传统高应变测试过程中由于混凝土开裂或出现严重塑性变形导致力信号失真的情况，将对高应变测试技术的完善作出有价值贡献。

图11 荷载作用结束时刻碟簧水平方向应力云图Fig.11 Horizontal Stress Nephogram of Disc Spring at the End of Load

图12 荷载作用结束时刻碟簧的应力云图Fig.12 Stress Nephogram of Disc Spring at the End of Load