基于协同约束进化算法的智能园区需求响应调度策略

张 聪, 陈 利, 胡茂凌, 朱颖骁, 李 翊, 陶竞立

(四川中烟工业有限责任公司, 四川 成都 610016)

0 引 言

随着电动汽车的普及[1]和用户用电需求的增加[2],传统的园区配电网络无法满足用户多种用能需求[3],智能园区越来越受到关注[4]。智能园区以高级量测体系(Advanced Metering Infrastructure,AMI)技术为支撑,综合多种智能用电控制设备,可以实现电能、信息和业务双向交互,能够有效促进新能源的消纳,并为用户提供多种增值服务[5]。需求响应(Demand Response,DR)作为智能园区的重要组成部分,可以通过能量管理控制器(Energy Management Center,EMC),引导电力用户参与到电网的互动中,可以有效降低负荷的峰谷差,减缓电网投资,保障电网的安全可靠运行[6-7]。

针对智能园区中的需求响应调度策略,国内外学者做了大量的研究。文献[8]把DR和储能系统引入到含风电的系统优化调度中,解决风电功率不确定性对系统稳定运行带来的影响。文献[9]提出了一种计及需求响应的旋转备用优化配置策略,以调度成本和备用成本最小为目标函数建立了优化组合模型,促进风电消纳。文献[10]利用基于ErLang开发的高并发实时数据采集平台和优化经济运行算法模型,开展智能园区充电优化控制研究。文献[11]提出了一种分布式的电动汽车有序充放电管理策略,由充电桩自主决策有序充放电计划,不用借助集中式通信系统实时监测和控制,适用于对大规模电动汽车的分布式管理。文献[12]建立了与用户互动的分布式储能多目标优化运行模型。文献[13]研究了微电网中储能的配置优化问题,降低微电网的运营成本。文献[14]面对工商业用户,通过制定不同的电力套餐,构建基于成本-效益分析的用户套餐选择模型。文献[15]结合用户的用电满意度,以用户用电成本以及系统负荷波动最小为目标,构建了两阶段的用户DR模型。

文献[8]和文献[9]针对发电侧,文献[10]和文献[11]针对电动汽车,文献[12]和文献[13]针对储能,文献[14]和文献[15]针对用户侧深入进行了研究。但是目前针对DR及源-储-荷综合优化调度的研究尚比较少,需要进一步进行研究。

本文以智能园区为研究对象,针对包含电动汽车、储能、光伏等分布式能源的用电场景,以系统总运行费用最低为目标函数,考虑电动汽车、储能等约束条件,利用协同约束进化算法进行求解,并与多种群协同净化遗传算法进行对比,最后借助算例分析优化模型和求解策略的有效性。

1 智能园区场景分析

典型智能园区用电场景如图1所示。智能园区用户的负荷可以分为以下几类[16]:① 基本负荷,是指用户在日常生活中必需的负荷,不能进行转移和调度,例如照明负荷;② 可转移负荷,是指拥有一定的时间弹性,在短时间内增加或减少负荷不会影响用户的使用体验的负荷,例如空调、热水器;③ 电动汽车负荷,是指电动汽车在充电过程中所消耗的负荷;④ 储能装置负荷,是指储能在充电的过程中所消耗的电能。此外,在智能园区内,还含有光伏发电装置。光伏产生的电能一方面可以满足用户的日常用电需求,另一方面在电能有剩余时也可以送入电网或者存储在储能装置中。光伏和储能装置一起构成分布式电源系统,参与智能园区内的能量优化和调度。

智能园区内每个区域都装配有智能电表和用电管理终端,可以根据用户的用能意愿更改对用户负荷设备的控制程度,实现用户和电网的双向互动,引导用户参与需求响应调度。本文中智能园区全部由同一售电公司供电,不考虑存在多家售电公司共同参与售电的场景。在计算电动汽车的充电功率时,本文选择恒功率充电方式,因为荷电状态(State of Charge,SOC)主要阶段在恒流充电阶段增加[17]。

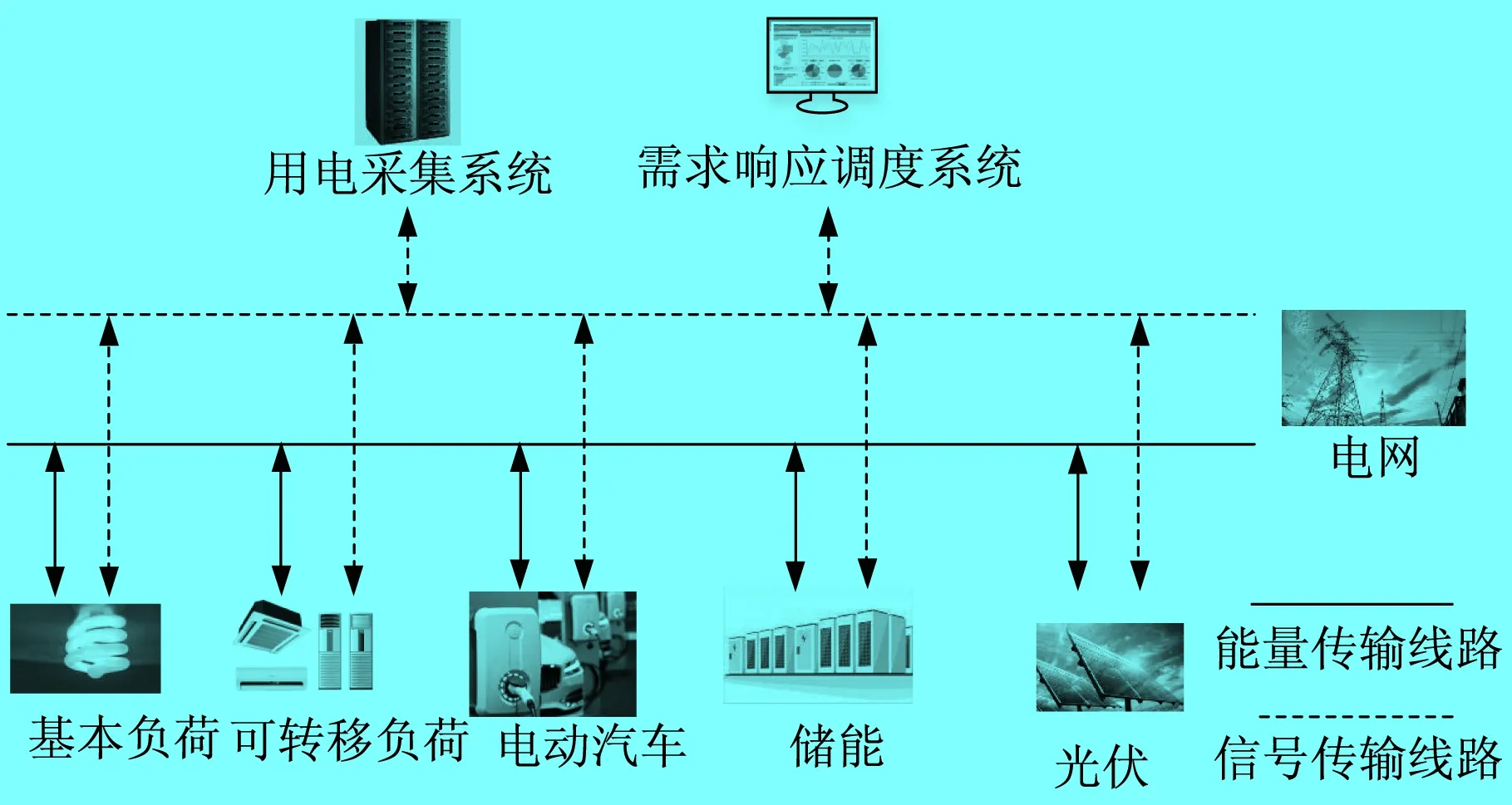
图1 典型智能园区用电场景

2 智能园区负荷调度模型构建

2.1 储能寿命模型

在整个储能生命周期内,储能循环充放电总量基本不变[18]。如果储能的更换成本固定,其替换成本为

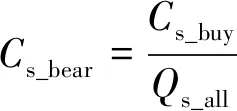
(1)

式中:Cs_bear——储能放电1 kWh的折旧成本;

Cs_buy——装置的购买成本;

Cs_all——装置全寿命周期输出的总电量。

储能装置的寿命主要受SOC的影响。放电时,SOC越高,对其损耗越少,寿命越长。储能SOC和寿命损耗系数表示为[19]

(2)

式中: SOC(t)—储能t时刻的荷电状态。

2.2 目标函数

本文智能园区优化策略目标函数是最小化运行费用。通过最小化园区的运行费用,可以降低园区从售电公司购买的电量,同时能够最大化地利用园区内部的分布式能源。目标函数表示为

(3)

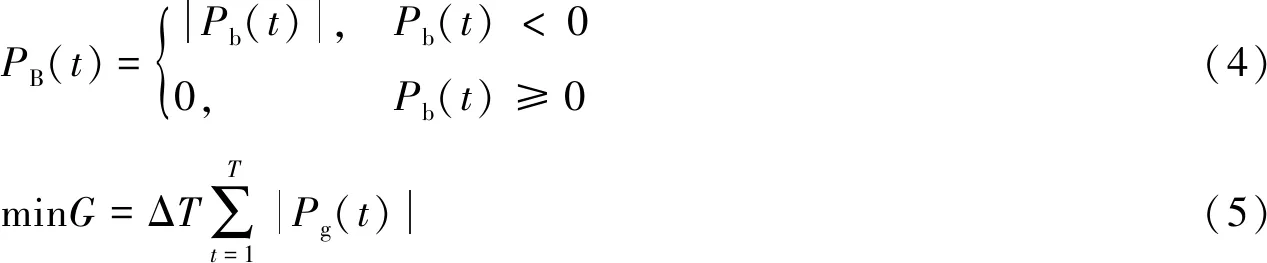
式中: ΔT——单位时间间隔;

T——优化时段数;

Pg(t)——单位时间间隔内与配电网交换的平均功率(购电时为正,售电时为负);

pr(t)——单位时间间隔内平均交易价格;

PB(t)、Pb(t)——t时段储能系统的放电功率和充/放电功率;

SOCmin——储能的SOC下限;

σ——惩罚系数。

式(3)中等号右边第1项为微电网与配电网的电能交易成本,第2项为储能装置的折旧成本,第3项为储能放电罚函数。

2.3 约束条件

(1) 功率平衡约束

Pb(t)+PEV(t)+PL(t)=Ppv(t)+Pg(t)

(6)

式中:Ppv(t)——光伏发电功率;

PL(t)——t时段负荷侧的固定负荷功率,可以通过短期负荷预测的方法得到[18];

PEV(t)——电动汽车在t时段的充电总功率。

(7)

(8)

(9)

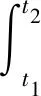
(10)

式中:PEV,n(t)——t时段第n辆电动汽车的充电功率;

N——电动汽车总数量;

Pavrg_n——第n辆电动汽车在充电时段内的平均充电功率;

tEV,n——第n辆电动汽车的起始充电时刻;

EEV,n——第n辆电动汽车在t2-t1时刻的充入电量,由第n辆电动汽车的电量需求量Ereq_n决定。

(2) 联络线功率约束

Pg(t)≤min{Pmax,PT}

(11)

式中:PT——配电变压器的额定功率;

Pmax——联络线路允许的最大传输功率。

(3) 储能装置约束

|Pb(t)|≤Pb_rat

(12)

(13)

Eb(t)SOCmin≤Eb(t)≤Eb_rat(t)SOCmax

(14)

Eb(0)=Eb(T)

(15)

式中:Pb_rat——储能装置额定功率;

Eb(t)——储能装置当前的荷电量;

Eb_rat(t)——储能装置额定荷电量;

ηb——储能装置充/放电效率;

SOCmax——储能系统SOC的上限。

(4) 电动汽车约束:

(16)

式中:PEV_rat——电动汽车充电电池的额定充放电功率;

SEV——电动汽车停留在充电站的时间段。

3 模型求解

本文采用协同约束进化算法求解智能园区优化调度模型。对于种群1,首先考虑目标函数以及违反约束的程度。在该种群内的适应度排序的原则可以表示为:① 不违反约束的解比违反约束的解要好;② 如果都违反约束,则违反程度小的解要好;③ 如果两个解都不违反约束,则目标函数值小的解适应度较好。通过该排序规则,种群1将首先搜索到可行域,然后再对目标函数进行优化,最终得到最优解。

可行域在决策空间是分割的(不连续),如果只采用一个种群进行进化搜索,极易导致算法收敛到局部最优解。为了避免算法收敛到局部最优解,在种群1基础上,引入种群2。种群2的适应度排序只考虑目标函数,不考虑违反约束的程度。因此种群2 将专注于获取问题在不包含约束的情况下的最优解。通过种群2能够有效地将算法拉出局部最优解,以找到整个全局最优解。

每一代中,首先两个种群各自产生后代1和后代2,然后将种群1、后代1、后代2合并并选取N个解组成新的种群1。种群2同理。最优解的获取是两个种群协同进化的结果。协同约束进化算法结构示意图如图2所示。

图2 协同约束进化算法结构示意图

4 算例分析

以某拥有固定充电桩的智能园区为例,通过对比优化前后储能和电动汽车的功率变化曲线,验证模型的有效性。

算例中智能园区安装有10台充电桩,每台充电桩的额定功率为10 kW;电动汽车的车载锂电池的额定电压为250 V,额定容量为100 Ah,电动汽车需求电量如图3所示。

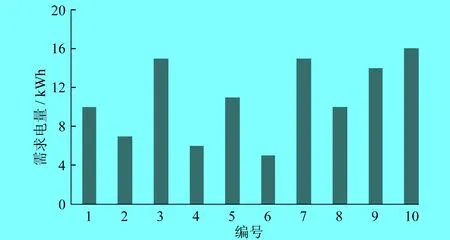
图3 电动汽车的需求电量

售电公司的电价采用分时电价。分时电价如表1所示[20]。

表1 分时电价

使用协同约束进化算法对该算例进行求解。相关参数设置如下:进化代数设置为200,每次进化后挑选个体100,变异概率0.6;优化时间周期为24 h,单位时间为1 h。

园区光伏出力和负荷情况如图4所示。

图4 园区光伏出力和负荷情况

采用协同约束进化算法求解的种群进化过程如图5所示,可以看到进化在40代达到最优值。根据文献[21],多种群协同净化遗传算法求解的种群进化过程如图6所示,其进化在400代才达到最优值。本文求解算法的收敛速度更快,效率更高。

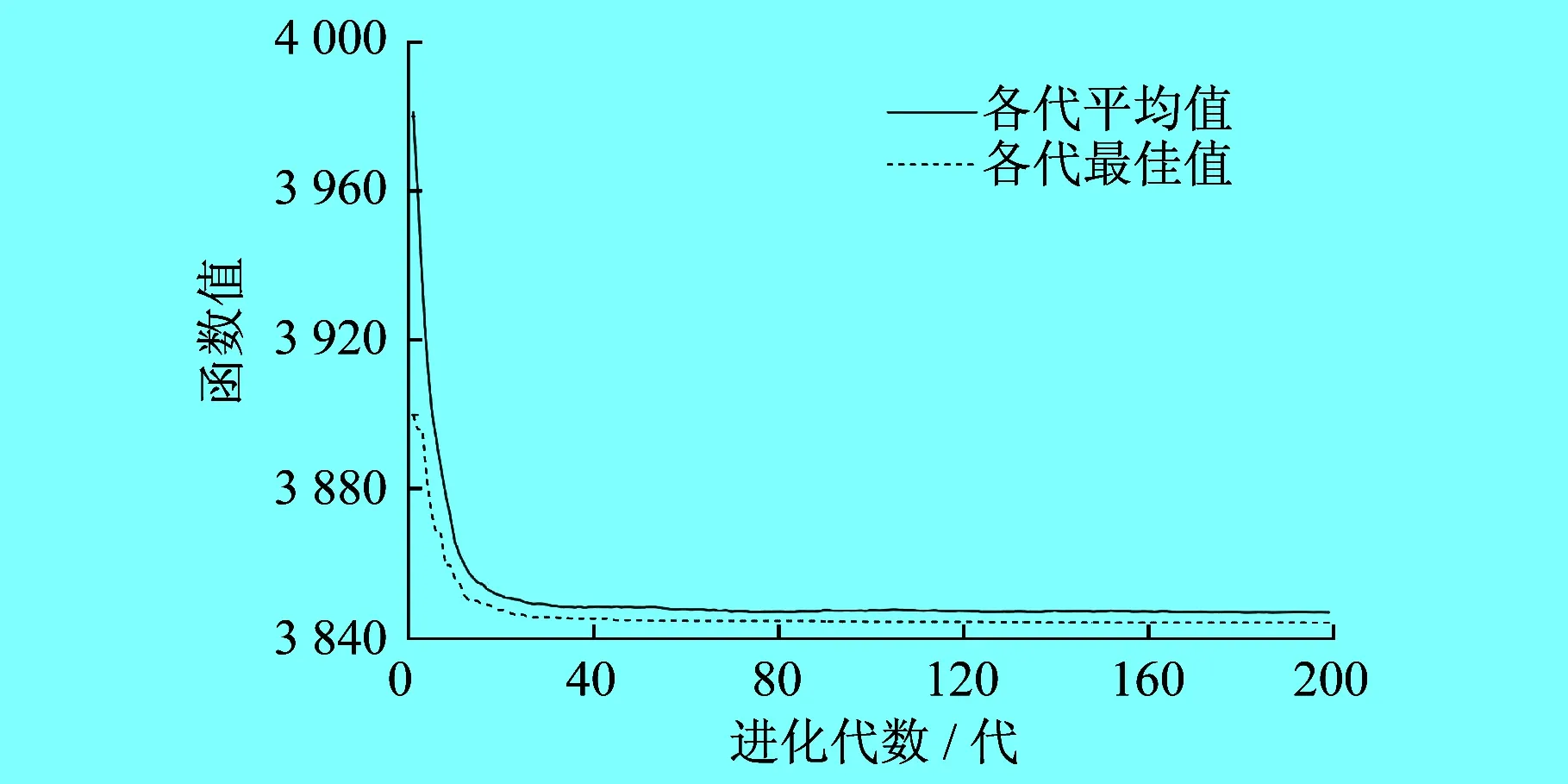
图5 采用协同约束进化算法求解的种群进化过程

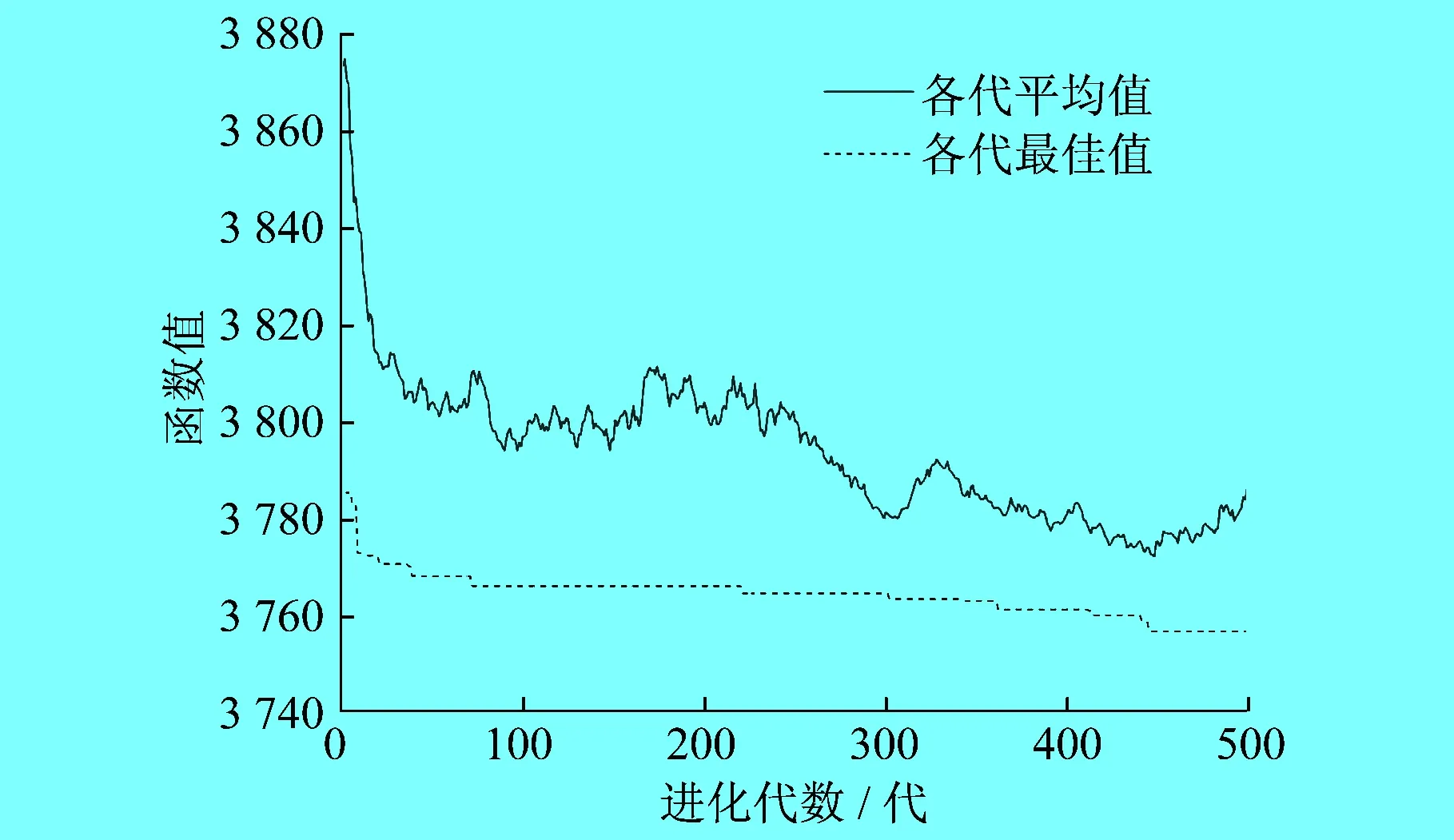
图6 多种群协同进化遗传算法求解的种群进化过程

优化后园区各元件有功功率变化如图7所示,优化后改变了电动汽车无序的充电状态。优化前电动汽车在电价峰时段也进行充电,优化后电动汽车集中充电时间在电价平时段,有效降低用户的用电费用。并且可以看到储能在电价峰时段,电源向外供电,满足负荷的用电需求。在光伏发电量大时,储能停止向外供电,优先利用光伏产生的电能,提高新能源的消纳率。

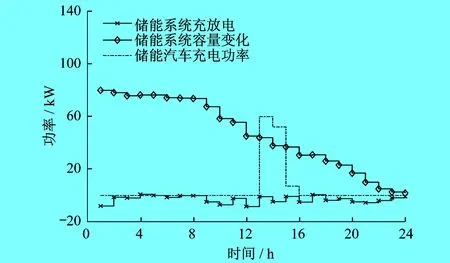
图7 优化后园区各元件有功功率变化

5 结 语

针对含有光伏、储能和电动汽车的智能园区用电场景下多种资源协同优化的问题,本文以智能园区用电费用最小为目标函数,构建了包含电动汽车、储能的智能园区优化调度策略,然后采用协同约束进化算法进行求解,验证了模型的有效性。

算例表明在该优化策略下可以实现智能园区内的电动汽车有序充电,并且可以与储能系统配合,进一步提高光伏的消纳率,降低园区用电费用。通过算法对比,也进一步证明该算法收敛速度更快,效率更高。下一步将融合深度学习技术,进一步研究实时电价考虑用户用能意愿背景下的智能园区优化调度模型。