基于QR-m-GARCH(1,1)-GED模型的人民币汇率隔夜风险测度
张建文, 唐国强, 杨静凌
(桂林理工大学 理学院, 广西 桂林 541006)
0 引 言
在经济全球化盛行的大背景下, 各国经济发展紧密相连。 作为世界第二大经济体的中国, 更是深深融入到世界之中。 在当代中国, 经济全球化很重要的一个标志就是人民币国际化。就目前的国际金融体系来看, 全球已经有40多个国家把人民币作为储备性货币。随着中国国际地位的提高和汇率市场改革的完善, 人民币的国际影响力不断提升[1]。近年来, 国际经济形势风云诡谲, 人民币汇率面临较强的升值压力。一旦人民币汇率发生大的波动, 将严重危害我国经济市场的平稳发展。人民币汇率波动的增加, 显著减小中国企业对外投资的可能性, 对银行业超额收益产生负向影响[2-3]。因此, 深入研究人民币汇率风险, 进而实现风险的防控与管控, 对我国经济市场平稳运行具有重大意义。
人民币汇率整日风险严格意义上可以分为日内风险和隔夜风险。其中, 隔夜风险是指前一天收盘到第二天开盘期间价格波动引发的风险, 但由于风险值较低, 只引起了小部分学者关注: 彭伟[4]提出了隔夜-AS模型和隔夜-SAV模型对隔夜风险进行测度; 简志宏等[5-6]使用CAViaR-EVT模型分别在左、 右尾分位数下对极端情况下的隔夜风险进行预测, 并采用HAR-CJ-M模型对高频数据进行隔夜风险的波动研究, 实现了隔夜风险的可预测。以上文献虽对隔夜风险进行了一定研究, 但隔夜风险作为整日风险的一部分, 极其隐蔽, 目前实证研究文献相对较少, 亟待丰富。本文基于QR-m-GARCH(1,1)-GED模型对人民币汇率隔夜风险进行研究, 既丰富在该方面的研究方法, 又丰富了研究内容。
金融领域的学者将VaR(风险价值)作为风险的测度指标, 故本文将其作为度量人民币汇率隔夜风险大小的指标, 在实际运用中, 学者们常借助GARCH类模型求解VaR值。申利[7]使用GARCH(1,1)模型推算人民币兑美元汇率数据的动态VaR; 申世昌等[8]使用GARCH类模型研究健康险收益率的波动性, 并对中国健康保险市场的VaR值进行度量; 曾裕峰等[9]以沪深300股指期货为研究对象, 使用GARCH模型求解VaR值, 发现广义误差(GED)分布相比正态分布和t分布风险的预测精度更优; 李世君等[10]采用偏t分布下的GARCH模型对消费行业的5个板块指数进行VaR求解, 失败率检验结果表明模型拟合效果较好。虽然使用GARCH类模型进行风险度量在金融市场已得到广泛应用, 但随着研究的深入, 也暴露出模型缺点。
GARCH模型需要预先设定误差服从的分布, 在一定程度上从模型自身角度加大了误差。由于分位数回归(quantile regression, QR)理论优良的统计特征, 部分学者开始将GARCH模型和分位数回归模型进行组合引入VaR的建模求解。陈耀辉等[11]采用QR-GED-GARCH模型和GED-GARCH模型对人民币汇率收益率风险进行测度, 将二者的拟合成功率进行比较, 发现QR-GED-GARCH模型更适合描述人民币汇率的数据特征; 涂振兴[12]采用历史模拟法、 QR-GARCH模型、 Gumbel Copula函数法, 对证券市场的4个指数进行研究发现, QR-GARCH模型更适宜刻画我国证券市场波动现象; 刘亭等[13]研究沪深综合指数的收益率数据, 建立QR-t-GARCH(1,1)模型与QR-st-GARCH(1,1)模型对指数收益率的风险特征进行全面描述; 王传美等[14]针对创业板的隔夜收益数据, 使用GARCH类模型与QR-GARCH类模型求解VaR, 发现QR-GARCH类模型得到的结果更准确。以上研究均表明, 将分位数理论与GARCH类模型组合后的模型能够较好地描述数据特征, 度量得到的风险结果更准确。
本文使用GARCH类模型与分位数回归模型的组合模型对人民币汇率进行隔夜风险的测度。由于美元指数在人民币汇率隔夜风险产生期间发生了完整的交易, 因此在GARCH类模型的均值方程中加入美元指数作为人民币汇率隔夜收益率的解释变量, 从中选取最优模型与分位数回归模型进行组合研究人民币汇率隔夜风险, 最终建立QR-m-GARCH(1,1)-GED模型求得VaR值, 同时将常数均值方程的QR-GARCH(1,1)-GED模型作为对照, 比较二者拟合成功率。
1 理论介绍
1.1 GARCH族模型
ARCH模型最早由Engle[15]于1982年提出, 但针对具有长期自相关性的数据进行拟合时, 会产生很高的移动平均阶数, 增加模型估计的难度, 从而影响ARCH模型的拟合精度。此后Bollerslev[16]在ARCH模型的基础上进行推广, 假设条件方差不仅受滞后一阶平方扰动项的影响, 而且受自身一阶滞后项的影响, 即广义ARCH模型——GARCH模型。低阶的GARCH模型已可以实现大部分非线性条件方差的刻画, 故使用GARCH(1,1)模型拟合人民币汇率隔夜收益率数据, 模型如下:
(1)
ut=σtεt;
(2)
(3)

将美元指数日对数收益率mt作为解释变量, 对应的均值方程如下
rt=at1mt+ut,t=1,2,…,T。
(4)
其中,at1表示美元指数变量前系数。
为弥补GARCH模型不能区分好、 坏消息给金融市场带来的不同影响, 学者们相继提出了非对称冲击模型, 如TARCH、 EGARCH、 PARCH模型。
TARCH模型是Glosten等[17]提出的, 可以衡量好消息和坏消息对条件方差带来的不同冲击, 并且可以检验数据是否具有杠杆效应。非对称模型的均值方程与GARCH模型相同, 不再重复列出, 仅将条件方差方程列出
(5)

EGARCH模型[18]又称为指数GARCH模型, 设定标准差与误差项之间满足更灵活的指数关系, 对应表达式如下
(6)
其中:ω,α,β,γ均为变量前系数。方程通过设定条件方差的对数形式, 反映呈指数函数变化的杠杆效应。
PARCH模型[19]模拟对象不再局限于方差, 而是标准差的δ次方。这样可以减弱条件方差受到大幅冲击时带来的影响。其方程为
(7)
其中:ω,α,β是常数;γ用来描述非对称效应;δ是标准差的幂指数参数,δ>0, 通过估计得出, 可以描述冲击带来的影响幅度。
1.2 VaR及计算方法
VaR指某金融资产在持有期L内, 在显著性水平α下, 可能遭受的最大损失值。设FL是金融资产L期内损失函数的累积分布函数, 记为FL(x)=P(L≤x)。VaR其实就是FL的α分位数, 表示为[20]
VaRα=inf(x|FL(x)≥α)。
(8)
在VaR值的计算方法中,方差-协方差方法最为流行, 最简单的就是借助GARCH模型的参数结果进行求解。以持有期1期为例, 给出3种分布下的计算公式。
1) 正态分布
(9)

2)t分布
(10)
其中:ν为自由度;tν(α)是对应的α分位数。
3) GED分布
(11)
其中:GEDα,ν,ε是GED分布在自由度为ν下的α分位数。
分位数回归使用参数估计的方法, 使误差绝对值的加权之和最小, 不需要假设误差项的分布, 从模型层面降低了拟合失败的风险。Taylor[21]将分位数回归模型引入VaR的求解。在置信水平为(1-α), 持有期为K期的金融资产收益率VaR的计算公式为
Vt,K(α)=β1,α+β2,αK1/2+β3,αK+β4,αK2+
(12)


(13)

2 实证分析
2.1 数据选取与描述性统计
本文选取人民币汇率作为研究对象, 选用1美元折合人民币金额的直接标价法表示汇率价格。实证数据为人民币汇率和美元指数的每日开盘和收盘价格。数据来源于同花顺软件, 选取的时间为2009-12-10—2019-08-23。
如果将相邻两天的收盘价的对数差定义为整日收益率r=lncloset-lncloset-1, 那么可以将其分为两部分: 日内收益率r1=lncloset-lnopent和隔夜收益率r2=lnopent-lncloset-1。按照上述定义, 根据时间顺序, 将人民币汇率隔夜收益率和美元指数日内收益率的时间关系表示为图1。美元与中国外汇市场的交易时间规律暗示着美元汇率日内收益的变动可能会对接下来开盘的人民币汇率产生一定的影响, 从而影响到人民币隔夜收益率, 即人民币汇率隔夜风险, 也就是前一天收盘到第二天开盘这段时间会受到美元指数影响的风险。

图1 人民币与美元的时间关系
拟合模型前, 先将人民币汇率序列与美元指数序列的日期进行比对, 剔除不重叠日期对应的数据。针对处理后的数据, 计算人民币汇率的隔夜收益率和美元指数日内收益率。由于数值量级过小, 为方便参数估计, 将人民币汇率隔夜收益率序列、 美元指数日内收益率序列放大100倍后再进行研究, 运行结果由Eviews 9.0和R语言实现。
借助人民币汇率隔夜收益率的时序图图2可直观地分析波动特征。可知, 人民币汇率隔夜收益率序列围绕着0值上下波动, 波动幅度在-1.2~1.2, 整体上序列处于平稳状态。但也观察到有多次明显的大幅上升和下降, 说明所选时间段内隔夜风险的确存在且不容忽视。以2015年8月11日汇率改革为分界线, 汇改前人民币汇率隔夜收益率除几次大的波动外基本保持平稳, 汇改后波动频率和幅度明显加剧。汇率改革提高了人民币汇率的市场化水平, 增强了外汇市场的透明度, 但也使得汇率的弹性变大。所选取的10年数据中, 2018年人民币汇率隔夜收益率波动最为剧烈, 这是因为货币政策分化和中美贸易战加大了人民币汇率的基本面压力。

图2 人民币汇率隔夜收益率时序图
为进一步分析人民币汇率隔夜收益率的数据特征, 对数据进行描述性统计分析, 结果见图3。人民币汇率隔夜收益率的均值为-0.001 7, 呈负收益特征; 标准差为0.121 9, 表明人民币汇率隔夜收益整体波动不大; 偏度为负数, 说明数据整体向左倾斜; 峰度为24.884 8, 远大于3, 说明数据的“尖峰”特征显著; J-B统计量为49 657.76, 其对应的p值为0, 表明样本数据不服从标准正态分布。

图3 人民币汇率隔夜收益率直方图和基本统计量
2.2 平稳性检验及格兰杰因果关系检验
为了从统计角度验证美元指数会对人民币汇率的隔夜风险产生影响的猜测, 借助Granger因果关系检验验证二者之间的关系。由于Granger因果关系检验对数据有平稳性要求, 故在进行检验之前, 先对数据进行平稳性检验, 防止出现虚假回归, 导致检验结果的不准确。采用ADF单位根检验对美元指数日内收益率与人民币汇率隔夜收益率进行平稳性检验, 结果如表1所示。可以看出, 两变量单位根检验对应的p值均为0, 说明在99%的置信水平下, 人民币汇率隔夜收益率序列和美元指数日内收益率序列均平稳。
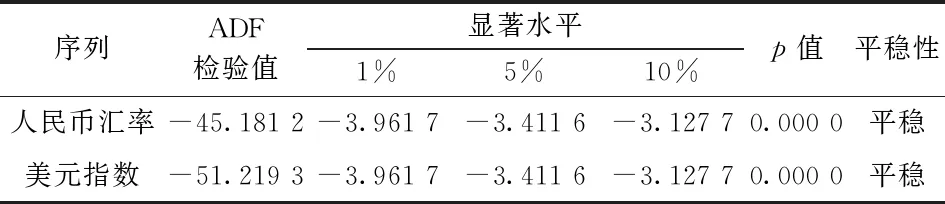
表1 单位根检验结果
在两序列均平稳的前提下, 对人民币汇率隔夜收益率序列和美元指数日内收益率序列进行格兰杰因果关系检验, 检验结果见表2。发现两个检验结论中只有一个拒绝原假设, 说明只存在一个单向格兰杰因果关系。在1%的显著性水平下, 美元指数是人民币汇率的格兰杰原因, 同时人民币汇率不是美元指数的格兰杰原因。这验证了美元指数日内收益率会影响人民币汇率隔夜风险的猜测, 证实可以将美元指数日内收益率作为人民币汇率隔夜收益率数据的解释变量。这也从侧面说明, 中国外汇市场存在被美国外汇市场引导的现象。

表2 Granger因果关系检验结果
2.3 ARCH效应检验
在建立GARCH类模型之前, 首先要检验人民币隔夜收益率序列是否具有ARCH效应特征。由于要建立两种不同的均值方程, 加入美元指数日内收益率序列作为解释变量的均值方程和常数均值方程, 故进行两次检验。使用拉格朗日乘数检验, 即ARCH-LM检验进行验证, 滞后1阶的ARCH-LM检验结果见表3。结果发现, 对应p值均为0, 表明在1%的显著性水平上拒绝原假设, 说明两种不同均值方程的残差序列具有显著的ARCH效应, 可以建立GARCH类模型。

表3 ARCH效应检验结果
2.4 模型的建立及VaR的求解
由于人民币汇率数据存在ARCH效应, 可以建立GARCH类模型来描述数据的“尖峰厚尾”特征, 消除异方差性。为获取更优的数据拟合效果, 建立4个不同的波动率模型GARCH、 TARCH、 EGARCH、 PARCH进行比较, 从中选出最优模型进一步分析。由于GARCH类模型普适性强, 低阶模型就能够很好地测量数据的时变特征。骆珣等[23]验证了GARCH(1,1)模型能较好地度量人民币汇率风险。故选用GARCH(1,1)、 TARCH(1,1)、 EGARCH(1,1)、 PARCH(1,1)模型, 在3种不同的分布(正态、t、 GED)下建模, 通过AIC(Akaike information criterion)和SC(Schwarz criterion)准则从中选出最优模型。由于前文已经证明美元指数是人民币汇率隔夜收益率数据的格兰杰因果原因, 故在模型均值方程中加入美元指数收益率数据作为解释变量, 同时将简单常数均值方程模型作为对照, 其中误差服从3种不同的分布, 每种分布对应8个模型, 共建立24种不同的模型, 信息准则结果如表4所示。

表4 各模型的信息准则结果
从误差服从不同分布角度分析, 仅有EGARCH(1,1)模型在误差服从t分布时, 对人民币汇率隔夜收益率数据的拟合优度高于正态和GED分布。另外7个模型, GED分布比正态、t分布对应的AIC和SC信息准则值更小,拟合优度更高。表明GED分布在测度人民币汇率隔夜风险的能力要优于正态和t分布。从均值方程角度分析,加入美元指数作为解释变量的m-GARCH类模型,比简单常数均值方程的GARCH类模型有更小的AIC和SC值, 且GED分布下两者差距更明显。 比如,m-GARCH(1,1)-GED模型对应的AIC值为-12.858 2,显著小于GARCH(1,1)-GED模型的AIC值-4.695 2。从整体上看, 24个模型中, 加入美元指数的m-PARCH(1,1)-GED模型的拟合优度最高, AIC值和SC值最小分别为-13.737 5和-13.718 8;其次是加入美元指数的m-GARCH(1,1)-GED模型, AIC值和SC值最小分别为-12.858 2和-12.844 0。GED分布下, 信息准则较优的两个模型及其对照模型的参数估计结果见表5。

表5 GED分布假设下模型估计结果
其中, PARCH(1,1)模型和m-PARCH(1,1)模型中捕捉非对称效应的参数γ对应p值为0.270 6和0.907 1均大于0.05, 参数不显著, 说明人民币汇率隔夜收益率数据不具有明显的杠杆效应。权衡参数显著性和拟合优度两方面, 选用m-GARCH(1,1)-GED模型刻画人民币汇率隔夜风险的波动特征。m-GARCH(1,1)-GED模型中方差一阶滞后项参数β对应p值为0, 参数显著, 表明隔夜风险受滞后风险的影响。
提取出m-GARCH(1,1)-GED模型所拟合的标准差, 绘制成时序图(图4)。标准差的变化反映了人民币汇率隔夜收益率的波动走势。为检验异方差性是否消除, 对标准化残差进行ARCH效应检验。结果显示调整R2统计量为0.990 6, 其对应的p值为0.000 1, 表明ARCH效应基本消除, 证明了模型的有效性。

图4 m-GARCH(1,1)-GED拟合的标准差的时序图
将m-GARCH(1,1)-GED模型拟合得到的条件方差和标准差估计值代入式(13), 在0.05、 0.01两个分位点下进行分位数回归, 求解VaR值。将5%和1%显著性水平下, QR-m-GARCH(1,1)-GED模型计算出的VaR与人民币汇率隔夜收益率真实值r绘制在图5中。可以看出, VaR值的动态走势与人民币汇率隔夜收益率波动走势相近, 表明QR-m-GARCH(1,1)-GED模型能很好地刻画人民币汇率隔夜风险的每日动态变化。

图5 QR-m-GARCH(1,1)-GED模型风险预测图
将QR-m-GARCH(1,1)-GED模型求解出的VaR值与人民币汇率隔夜收益率真实值进行比较, 计算拟合成功率, 拟合成功率越高说明模型的拟合效果越好。同时与常数均值方程的QR-GARCH(1,1)-GED模型的结果进行比较, 结果见表6。

表6 拟合VaR成功率结果
在5%和1%显著性水平下, 加入美元指数作为解释变量的QR-m-GARCH(1,1)-GED模型对VaR的拟合成功率为99.52%和92.15%。QR-m-GARCH(1,1)-GED模型在5%的显著性水平下的预测结果最接近理论值, 但在1%显著性水平下拟合成功率不如QR-GARCH(1,1)-GED模型, 这表明QR-m-GARCH(1,1)-GED模型在高显著性水平下更有优势。5%的显著性水平下, 均值方程中加入美元指数的QR-m-GARCH(1,1)-GED模型与QR-GARCH(1,1)-GED模型相比, 拟合成功率增加了0.79%, 这在一定程度上验证了美元指数价格波动与人民币汇率隔夜风险密切关联。
3 结束语
由于中国和美国外汇交易市场开盘和收盘时间不同, 使得美元指数价格波动对人民币汇率隔夜风险产生影响。本文在人民币汇率隔夜风险的研究中, 加入美元指数作为人民币汇率隔夜收益率序列的解释变量, 建立QR-m-GARCH(1,1)-GED模型进行实证研究, 同时与常数均值方程的QR-GARCH(1,1)-GED模型进行对比。结果发现: 1)所选数据期间, 人民币汇率隔夜风险的确存在, 并且汇率改革后波动明显加剧; 2)人民币汇率价格走势存在被美元指数引导的现象; 3)人民币汇率隔夜风险受滞后风险的影响; 4)相比QR-GARCH(1,1)-GED模型, 加入美元指数的QR-m-GARCH(1,1)-GED模型在高显著性水平下拟合人民币汇率隔夜风险更具优势。
本文将美元指数作为人民币汇率隔夜收益率的解释变量, 区别于以往的常数均值方程, 更能体现我国外汇市场受美元指数价格波动的影响。使用QR-m-GARCH(1,1)-GED对人民币汇率隔夜风险进行研究, 为央行和广大投资者提供决策参考, 具有重要的理论和现实意义, 也为深入研究美元指数与人民币汇率价格之间的关系提供了研究依据。

