基于业务指标关联度分析的可靠性规划问题研究

高崇，曹华珍，吴亚雄，李浩，张瀛，王承民，胡聪

(1. 广东电网有限责任公司电网规划研究中心，广州510080；2.上海交通大学 电子信息与电气工程学院，上海200240)

0 引言

随着社会经济的加速增长，人们的生活和社会的生产对电力系统的要求越来越高。配电系统被赋予尽可能可靠地将电能供给各种用户的任务。安全、可靠成为电力系统供电特点的两大不可或缺的因素[1 - 3]。因此，可靠性就成为配电系统规划决策中的常规性工作。1969年，加拿大学者R.Billinton教授发表了关于电力系统可靠性的第一篇学术论，电力系统可靠性领域至此开始了快速的发展。随着电力企业管理方式的改变和管理水平的提高以及电力服务承诺制的发展，电力系统可靠性在社会生产工作中的位置越发重要。近年来，人们对配电系统可靠性的重视程度大大提高。电力系统可靠性的指标在配电网中的落实方法也被提出了新的要求。

由于配电网管理分层分级的特征，在上级确定可靠性指标的目标值后，需要向下级传达业务指标的控制目标。可靠性指标空间分解方法运用灵敏度分析方法得出各业务指标对可靠性指标的灵敏度，从而将可靠性目标分解为各个地区业务指标的控制目标。再根据投资估算得出各项业务指标提升所需的投资金额。

文献[4 - 5]分别利用二分法和层次分析法分析求解最优分解目标值，利用成本效益分析进行配电网可靠性目标规划。文献[6]以显式公式形式实现配电网可靠性指标的求解，通过配电网可靠性提升措施与可靠性参数及可靠性指标的关系，研究配电网可靠性提升措施对可靠性指标的影响。

文献[7]针对分区可靠性计算不能灵活组合合成的问题,提出全网供电可靠性指标的合成方法。文献[8 - 17]提出了不同场景下可靠性投资优化的方法。

以上文献提出的可靠性指标分解模型，是在局部空间实现可靠性指标分解，缺乏将全网可靠性指标与各个区域具体业务指标建立关联关系从而实现可靠性指标的空间分解的模型。在模型求解上，是在各个区域内部达到了投资优化，没有在全网范围内以投资最小为最优目标。

针对上述问题，本文提出一种投资最优的可靠性指标空间分解模型。通过对各个分区业务指标进行成本效益比计算，用用户数加权处理后，在全网范围内进行优先级排序，将可靠性指标按此顺序进行空间分解，落实到各个分区的具体指标，从而实现全网的投资结构最优化。克服了以往确定可靠性提升目标时的盲目性，减少了由于没有在全网范围内以投资最小为最优目标造成的额外投资。

1 业务指标关联度分析与投资估算

在规划阶段，主要通过对网架结构的优化实现对可靠性的提升，与之相关的业务管控指标通常包括可转供电率、电缆化率、平均线路长度、平均线路分段数等，配电自动化也会对供电可靠性有较大影响。此外，线路和配变的负载率也可能影响转供能力，结合实际投资需求，选取相关性较强的可转供电率、馈线自动化覆盖率、电缆化率和架空线平均分段数4个业务指标对地区i供电可靠性进行投资优化[18]。平均故障停电时户数Ui·SAIDI-F与4个业务指标之间的关联关系可表示为：

Ui·SAIDI-F=RliSli+RaiSai+RciSci+RsiSsi+b0

(1)

式中：b0为常数项；Rli、Rai、Rci、Rsi分别为可转供电率、馈线自动化覆盖率、电缆化率和架空线平均分段数4个业务指标的具体数值；Sli、Sai、Sci、Ssi分别为Rli、Rai、Rci、Rsi的灵敏度，在实际计算中，根据过去几年的平均故障停电时户数与4个业务指标的历史数据，运用关联分析法[19]、回归分析法[20]或改进熵权法[21]等，计算出指标Rli、Rai、Rci、Rsi的灵敏度。其物理意义是：某个业务指标提升了一个单位，使得平均故障停电时户数下降的量值[19]，例如：

(2)

由于规划电网难以收集到具体的电网拓扑信息，因此本文未采用常用的解析法进行可靠性评估和灵敏度计算，而采用基于数据驱动的回归分析法进行灵敏度计算。在工程中，每个业务指标对应一种典型的工程场景。针对这4个业务指标分别构建4种业务指标提升的典型工程建设场景，具体包括以下方面。

1)针对现有线路增加一个联络点提升可转供电率，投资估算为：

Cl=Ll(co+rcr)+cb

(3)

式中：Ll为联络线长度；co为架空线或电缆单位造价；cr为安装线路的单位成本；r为施工系数；cb为开关单位成本。

2)进行馈线自动化建设改造提升馈线自动化覆盖率，投资估算为：

(4)

式中L为架空线全长。

3)新建电缆线路，提升电缆化率，其投资估算为：

Cn=L(cc+rcr)+Uct

(5)

式中L为电缆线全长；cc为电缆单位造价；cr为敷设单位成本；U为平均中压用户数；ct为配变单位成本。

4)对现有架空线增加一个分段开关，提升架空线平均线路分段数，其投资估算为：

Cs=Nocb

(6)

式中：No为架空线路条数；cb为柱上开关单位成本。

2 可靠性规划问题

2.1 数学模型

基于投资额最小化的可靠性指标空间分解模型的目标函数如式(7)所示。

(7)

式中：Cli、Cai、Cci、Csi分别为区域i的4项具体业务指标提升所需投资。下面介绍模型的等式约束。

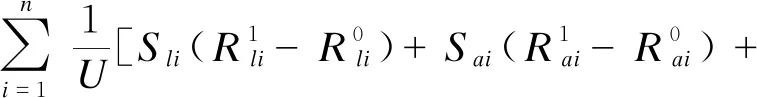
(8)

式中：Sli、Sai、Sci、Ssi分别为区域i的4项具体业务指标的灵敏度。U为各区域的中压用户数之和，ΔSAIDI-F为平均用户故障停电时间的目标下降值。

(9)

(10)

(11)

(12)

模型的不等式约束如下所示。式(13)—(16)代表各指标的提升空间的范围约束。

(13)

(14)

(15)

(16)

上述式(7)—(16)即为可靠性指标空间分解模型的数学表达。在该优化模型中，各地区的各项业务指标是优化变量，为了确定目标函数的凸性，将各区域业务指标每减少相应时户数所需的成本代入式(7)，其Hessian矩阵只有对角线上含有电缆化率的项不为0，是半正定矩阵，因此其目标函数是凸函数。式(8)是等式约束，式(13)—(16)是不等式约束，易知其构成的集合是凸集。因此该模型为凸规化问题，局部最优解即为全局最优解。

为了求解该模型，首先计算区域的可靠性指标的成本效益比。成本效益比是指该区域每减少相应停电时户数所需的成本。如Cli/Sli即为可转供电率的成本效益比。然后用各个区域的用户数将各区域的各可靠性指标的成本效益比进行加权处理，在全网范围内按照各区域各指标成本效益比从低到高的顺序确定投资优先级排序。

分析各指标的成本效益比特性可以发现，可转供电率、馈线自动化覆盖率、和架空线平均分段数3个业务指标的成本效益比是常数，不随指标当前值变化而变化。如式(9)、(10)、(12)所示。但电缆化率的成本效益比会随当前的电缆化率的提高而增加，如式(11)所示，将其改写为式(17)。

(17)

式中：ΔRci是电缆化率指标目标值和现状值的差值；ki为人为定义的系数，其定义已在式中给出。为了保证当前投资的指标始终是成本效益比最低的指标，在提高某区域的电缆化率时，还应统筹考虑其他区域的该项指标成本效益比。在工程实际中，电缆化率成本效益比往往比较大，其投资的优先级也常常最低。假设某系统有A、B两个电缆化率投资优先级相邻的区域，先提升区域A的电缆化率，直至两地电缆化率成本效益比相等。然后，需要保持它们相等，同时投资，从而达到投资结构的最优化。有如下方程：

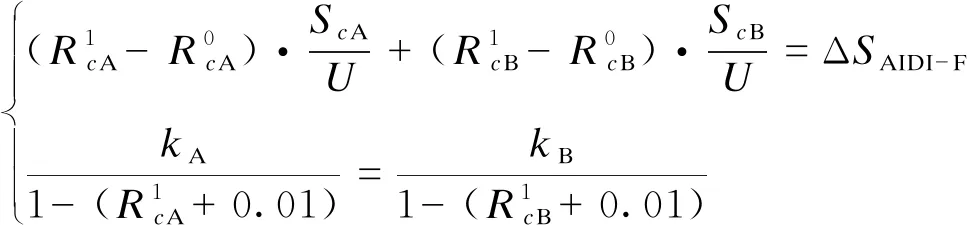
(18)

式中：kA和kB为前文定义的系数。电缆化率提升所需投资用成本效益比的积分平均值进行计算，如式(19)所示。

(19)

2.2 求解步骤

模型求解流程图如图1所示。模型求解步骤如下。

1)将全网可靠性指标与各区域业务指标建立关联关系，计算其灵敏度。

2)计算各指标投资估算，将成本效益比进行加权，计算各区域各项业务指标提升所需投资，并依次确定投资顺序。

3)按照上述顺序投资，直到SAIDI-F达到目标值。

4)计算各区域业务指标当前值和投资额。

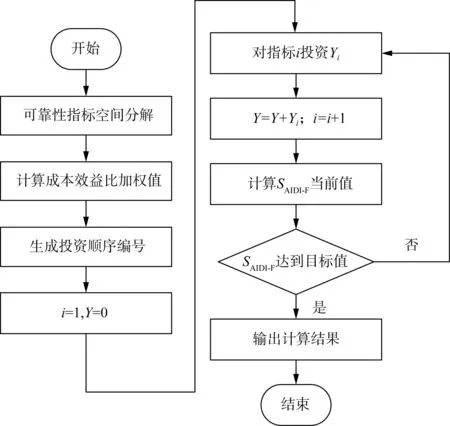
图1 模型求解流程图Fig.1 Block diagram of model solving process

3 算例

某系统有A、B、C 3个区域，当前中压用户数分别为67 734、76 514、19 334，合计163 582。目标将全网停电时间降低30 min，下面进行计算。首先根据历史数据计算各业务指标灵敏度。以A区域为例，其可靠性指标与业务指标历史数据如表1所示。

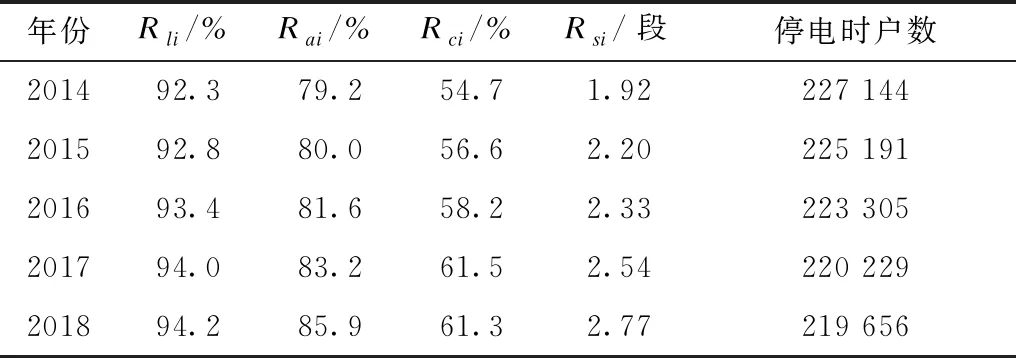
表1 A区域可靠性指标与业务指标历史数据Tab.1 Historical data of reliability indicators and business indicators of region A

用回归分析法计算A区域的回归方程，得到四项业务指标对应的回归系数为208.85、128.69、780.07、1 221.47，即A区域业务指标的灵敏度。同理可得B，C区域的业务指标灵敏度结果如表2所示。

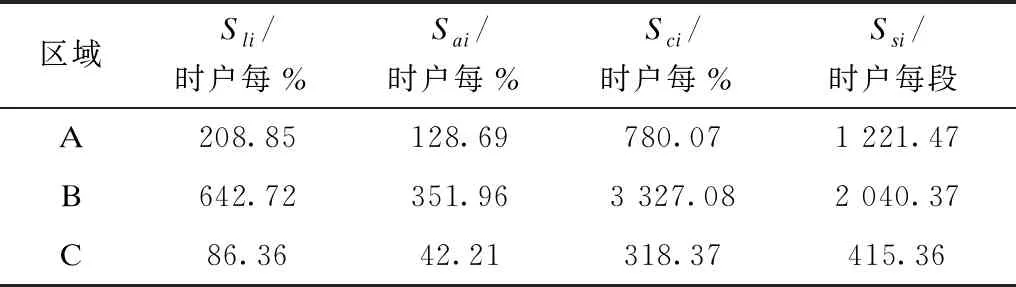
表2 各区域业务指标灵敏度分析结果Tab.2 Results of sensitivity analysis of business indicators by region

通过各指标的成本效益比，除以各区域的用户数后，得到每减少相应时户数所需的成本，如表3所示。

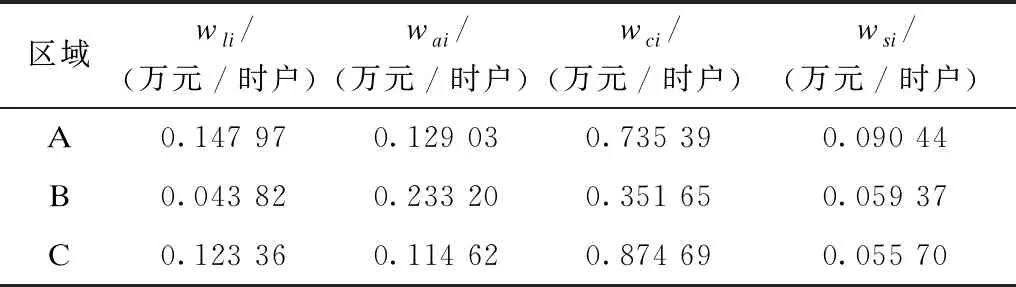
表3 各区域业务指标每减少相应时户数所需的成本Tab.3 Cost-benefit ratio after weighting of business indicators in each region

统筹比较各个指标的成本效益比，按照从小到大的顺序进行投资优先级排序，从而提高可靠性。当3个城市的可转供电率，馈线自动化覆盖率，架空线平均分段数都提高到满额后，全网减少停电时间13 min。然后选取此时成本效益比最低的区域B的电缆化率进行投资，当其成本效益比提升至与区域A相等时，全网的减少停电时间为26.35 min，接下来对A、B两区域的电缆化率指标同时进行提升，用式(15)进行计算。最后得到各指标的控制目标，如表4所示。

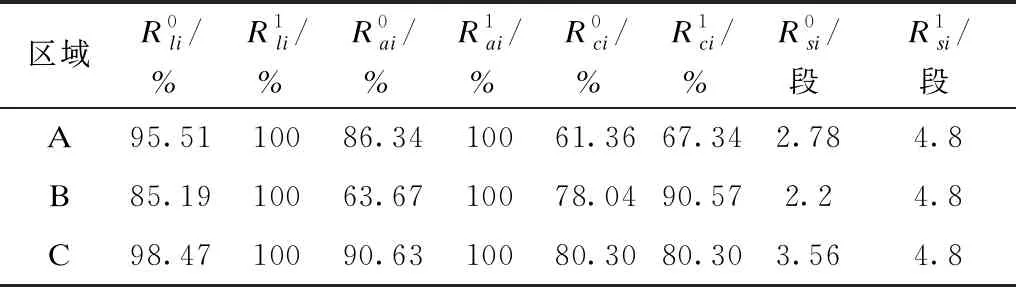
表4 各区域业务指标的初始值和目标值Tab.4 Initial value and target value of business indicators by region

最后，根据成本效益比计算投资额，如表5所示，合计投资总额为3.061 2亿元。

上述方法分析过程较为具体，在仅需要确定各项业务指标的投资目标的情况下，可以利用MATLAB优化工具箱进行求解。将目标函数和约束条件写入文档，选择有约束的非线性求解器，用内点法进行求解。输入各个业务指标上下限，从零点开始求解，大约耗时9 s。

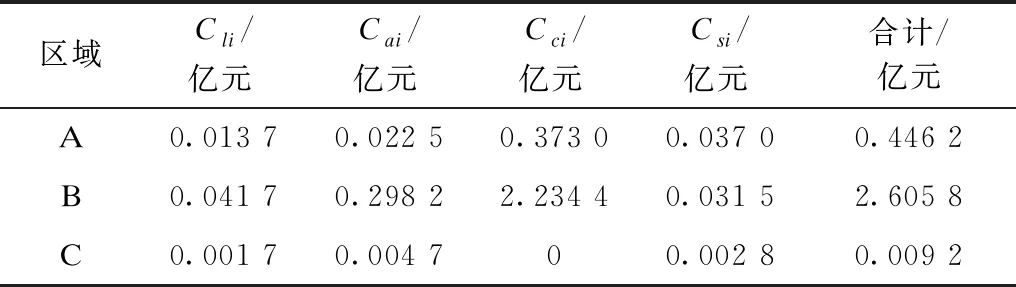
表5 各区域各项业务指标提升所需投资Tab.5 Investment required to improve business indicators by region

如果采用传统的投资优化模型，由上级系统分别向各区域下达各区域的平均用户故障停电时间SAIDI-F的目标下降值后，在各区域内部进行4项业务指标的投资优先级排序。现假设3个分区的初始平均用户故障停电时间相同，上级对3个地区下达的平均用户故障停电时间减少目标按照等比例下降幅度进行分配，A区域可靠性指标减少30 min，则其业务指标控制目标计算结果如表6所示。

表6 传统模型的A区域业务指标的控制目标Tab.6 Control targets for business indicators by region A of traditional model

用A区域电缆化率成本效益比的积分平均值计算提升电缆化率所需投资，将Δt=0.5,h,RCi1=98.18,RCi0=61.36,ki=27.68,U=67 734代入式(18)，得出C=8.27亿元。 可见仅此一项投资就远超本文提出的可靠性指标空间分解模型的投资预算。说明该模型确实能减少投资金额。

4 结语

本文提出了可靠性指标空间分解模型。将各区域的成本效益比进行加权处理，使各区域的业务指标可以在全网范围进行统筹分析比较，得出在全网所有业务指标的投资优先级排序，从而实现了投资最优化。在算例中，对某个由3个区域组成的系统进行了两种投资方案的比对，验证了本文提出的投资优化模型的优越性。

在指标空间分解完成后确定投资顺序时，本文给出了对两区域电缆化率同时进行提升的计算方法。在复杂配电系统中，可能出现需要对多个区域的电缆化率指标同时进行提升的情况，需要进一步研究。在此基础上，可以研究对应的计算机算法。