室间质评数据计算偏倚和σ值的三种方法比较分析
贾建美,刘春霞
(南通瑞慈医院检验科,江苏 南通226010)
σ在数理统计中表示“标准差”,表征任意一组数据或过程输出结果的离散程度的指标[1]。6σ质量管理曾被广泛应用于各大企业的质量管理中,后来被应用到临床实验室质量管理中[2,3]。6σ质量水平,意味着百万机会中只有3.4个缺陷的可能[4]。根据公式σ=(TEa-|Bias|)/CV可以计算出σ值,其中TEa为允许总误差(%),Bias为偏倚(%),CV为变异系数(%)。TEa、Bias和CV均可影响σ值。大部分文献中Bias来源主要是全国常规化学室间质量评价报告,但是不同的计算方法结果并不一致。本研究利用室间质评数据,选用三种不同计算方法,以卫生行业标准WS/T403-2012作为质量规范[5],对这三种方法所得Bias以及相应的σ值进行分析比较。
1 材料和方法
1.1 材料2017-2018年本室参加的全国常规化学室间质评数据,共21个项目,包括钾、钠、氯、钙、磷、葡萄糖、尿素、尿酸、肌酐、总蛋白、白蛋白、总胆固醇、甘油三酯、总胆红素、丙氨酸转移酶、天门冬氨酸转移酶、碱性磷酸酶、淀粉酶、肌酸激酶、乳酸脱氢酶、γ-谷氨酰转移酶。室内质控数据来自江苏省室内质控上报系统2018年2-9月份的本室上报数据。
1.2 仪器和试剂 OLYMPUS 2700全自动生化分析仪,室内质控品由RANDOX公司提供,批号为1227UN(低值)、909UE(高值)。
1.3 精密度水平评估 选本实验室2018年2-9月份常规化学的室内质控累积在控变异系数(CV)作为该实验室精密度水平。CV合并=和CV2分别为两个浓度水平的累积在控CV(较大CV与较小CV的比值小于2时)。
1.4 偏倚评估 ⑴取本实验室2018年常规化学3次室间质评数据计算偏倚:相对偏倚=[(|本室测定值-靶值|)/靶值]×100%,计算所有相对偏倚的平均值(Bias1);⑵以本室测定结果为X,EQA靶值为Y,得出回归方程Y=aX+b。将本室室内质控两个浓度水平的累积均值x代入方程,得出y。根据公式Bias=[(y-x)/y]×100%[6],得到低、高两个偏倚值,利用得出Bias2。⑶取2017-2018年EQA数据中浓度跟本室室内质控相近的数据(至少6次),包括低、高浓度两个水平,计算“方法和实验室偏倚(RMSbias)”。RMS-为单次室间质评的相对偏倚,n为室间质评数据的个数[7]。同样每个项目得到低、高两个bias值,计算合并bias得出Bias3。
1.5 总误差(TEa)以卫生行业标准WS/T403-2012作为质量规范。
1.6σ值的计算 σ=(TEa-|Bias|)/CV。
1.7 统计学分析 用SPSS17.0软件包进行统计学处理,采用ANOVA统计学方法,P<0.05为差异具有统计学意义。
2 结果
2.1 精密度 各检测项目的累积CV1,CV2以及CV合并见表1。

表1 2018年2-9月份各项目的CV1,CV2以及CV合并(%)
2.2 Bias和σBias1、Bias2、Bias3及相对应的σ1、σ2、σ3值见表2~4。
2.3Bias1、Bias2和Bias3差异性分析Bias1与Bias2,Bias2与Bias3,Bias1与Bias3差异均有统计学意义,存在显著性差异。P值分别为0.001、0.000、0.043,均小于0.05。
2.4 σ1、σ2和σ3差异性分析 σ1与σ2,σ2与σ3,σ1与σ3差异均无统计学意义。P值分别为0.566、0.359、0.730,均大于0.05。
3 讨论
实验室质量管理引入6σ管理技术,能更直观的反映实验室整体质量水平,并为检验项目质控规则的个性化选择提供依据。
精密度是在规定条件下,对同一类或类似被测对象重复测量所得示值或测得值间的一致程度,通常用CV来表示。本室精密度选用8个月的室内质控累积在控数据估算各项目CV,其中包含了质控品和试剂批号更换、仪器的校准、人员更换等影响因素,能够较真实地反映本实验室的CV水平[8]。
偏倚是系统测量误差的估计值,指同一实验室用同种方法多次独立检验分析。同一样本所得结果的均值与靶值之间的差异,是检验结果正确度指标。偏倚的来源有以下几种:⑴根据参考方法、参考物质计算偏倚。⑵参与正确度验证计划。⑶常规室间质评评价计划[9]。参考方法和参考物质由于各种原因均不适用于临床实验室。正确度验证计划是采用无基质效应的新鲜冰冻血清,用参考方法确定靶值,不需要分组,实验室测定结果直接与靶值比较,能够比较真实地反映偏倚。但该计划费用较高,测定次数多,不适合所有实验室[10]。因此大多数实验室常以EQA结果来估算偏倚。利用EQA数据估算偏倚有很多方法,最简单、使用最广泛的是取同一项目所有批号的相对偏倚,计算其相对偏倚绝对值的平均值(Bias1);第二种计算方法是以本室测定结果为X,EQA靶值为Y,做相关回归统计得到回归方程Y=aX+b。再将本室室内质控两个浓度水平的累积均值x代入方程,计算y。根据公式Bias=[(y-x)/y]×100%,得出两个偏倚值,最后计算合并Bias(Bias2);第三种计算方法是利用若干次的EQA数据,选取其中与本室室内质控浓度相近的数据(至少6次),先计算单个相对偏倚,然后根据公式计算方法和实验室偏倚(RMSbias),得到两个偏倚值,最后计算合并Bias(Bias3)。本研究对这3种偏倚结果进行了比较分析。利用统计软件分析,三种偏倚之间均存在显著性差异(P<0.05)。结果表明,即使同样采用EQA数据,不同的计算方法得出的偏倚结果也有明显差异。
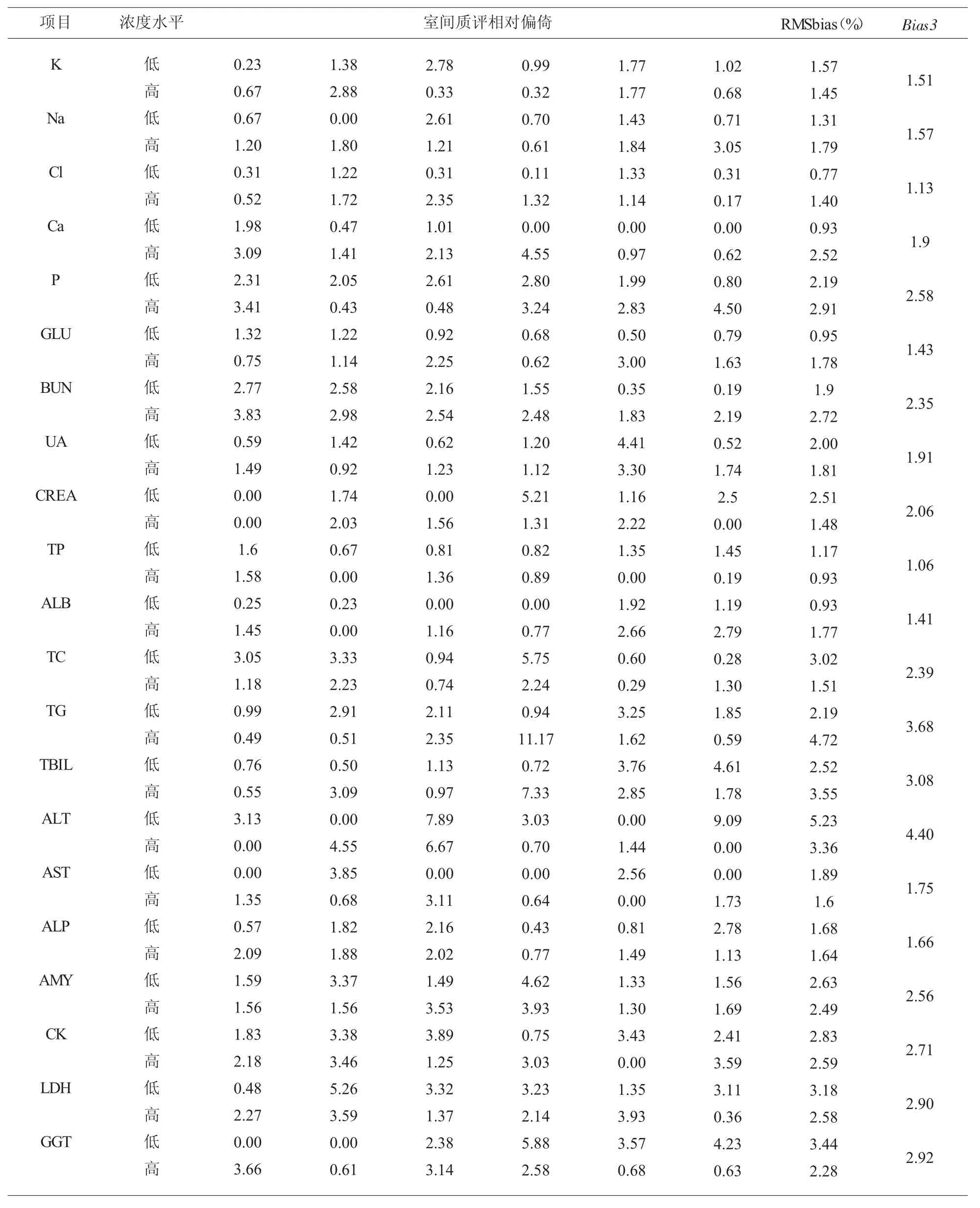
表3 方法和实验室偏倚(RMSbias)以及Bias3(%)
以卫生行业标准WS/T403-2012规范的TEa,根据公式σ=(TEa-|Bias|)/CV,得到三组不同的σ值。统计软件分析结果显示各σ值之间无显著性差异。虽然不同计算方法所得偏倚有显著差异,但其相对应σ值之间无明显差异。也就是说不同的偏倚计算方法对某个项目的σ值结果无明显影响。三种偏倚的计算方法中绝对值的平均值是最简单的、也是应用最广泛的,其它两种计算方法比较繁琐、耗时较长。但利用EQA数据计算偏倚也有一定的局限性,其靶值的建立是基于对等组内结果取均值,实际是实验室公议值,并非真值[11]。Friedecky等认为,EQA结果应该与参考方法的靶值进行对比,要求计量可溯源性和绝对正确度[12]。国家卫计委临检中心的正确度验证计划是比较可行的获得偏倚的方法,但是未得到广泛的应用。

表4 行业标准TEa(%)、CV合并(%)、Bias(%)以及σ值
根据Westgard西格玛多规则的评判标准可以看出σ值越大,质量水平越高,质控规则越少。反之,σ值越小,质量水平越低,质控规则越多[13]。根据项目σ值的不同,可以选择不同的质控规则,而不是所有检测项目均采用同样的质控规则[14]。表4结果显示,有10项σ≥5,达到优秀水平,但仍有7项σ≤3,水平欠佳,说明本实验室的检测性能有待提高。例如UA的σ水平已经大于10,达到世界一流水平,质控规则只要求13s。而Ca的σ水平最低,低于3。根据质量目标指数QGI=Bias/(1.5×CV),Ca的计算结果为0.74,小于0.8,提示该项目性能不佳的原因主要是精密度超出允许范围,CV相对较大,需要优先改进精密度,以改善实验室的质量控制水平[15]。
总之,无论采用哪种偏倚计算方法都能较为真实地评估σ值,从而反映本实验室的检测水平,也是目前较为行之有效的方法。三种偏倚计算方法在文献中较常见,但三种方法比较分析较少见,所得σ值比较尚未见到。文中比较项目均为临床生化项目,对其它检测项目是否适用还需要进一步深入研究。

