舰载传感器测量误差链分析

何佳洲，罗志勇，潘江怀

（江苏自动化研究所，江苏 连云港 222061）

0 引言

人类对客观事物的质、量及其相互关系的认识都离不开测量。著名化学家门捷列夫说：“科学始于测量”；数学家雅科比认为：“没有测量就没有任何精密科学，就没有任何应用数学，就没有任何实验。新的测量方法标志着真正的进步”。

与固定基座传感器不同，舰载传感器的基座相对于水平面是不稳定的，因为舰艇在运动过程中会发生纵摇、横摇、升沉以及艏向改变，尤其是纵摇、横摇和艏向改变对传感器的探测结果具有非常大的影响，因此，动平台传感器需要一个稳定平台来补偿载体姿态对传感器测量的影响［1-3］。传统方式是将传感器架设在机械稳定转台上［4-5］，稳定转台在纵摇轴和横摇轴上各有一套伺服驱动装置，当平台发生纵横摇时，伺服系统根据接收到的控制信号，由驱动系统使稳定转台的纵横摇作出相对应的转动，从而保持传感器天线座的始终水平。随着计算机技术和电子扫描雷达技术的发展，出现了电子稳定平台［6-10］，电子稳定平台并不通过机械手段去保持传感器测量坐标系的物理水平，而是依据载体纵横摇信息控制传感器波束指向，采用数学手段即时修正载体摇摆的影响，将传感器原始测量转换到当地水平面。

两种稳定方式误差链的分析大同小异，本文后续以电子稳定方式为例进行说明，针对舰艇平台传感器探测过程，分析其各环节测量误差链的传递和演化。具体涉及：传感器的探测、传感器的姿态、平台的位置、平台的姿态、平台的时间同步等测量误差，讨论其对目标定位精度的影响。

1 坐标系及其转换误差分析

下面介绍舰载传感器数据处理涉及的坐标系。

1.1 坐标系

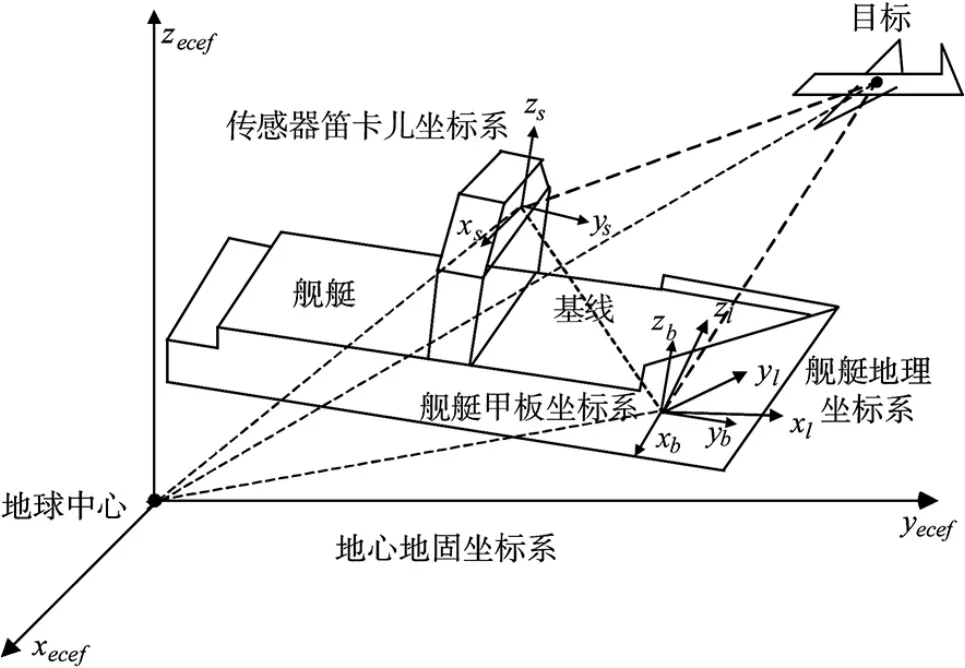
图1 舰载传感器数据处理涉及坐标系的示意图

如图1 所示，多平台传感器信息融合时，舰载传感器数据处理涉及的主要坐标系包括：

1）传感器球坐标系

以传感器为中心建立的球面坐标系，空间点的位置用该点相对于传感器的距离r、方位角β 和俯仰角ε 描述。后续用“DBE”代指传感器球坐标系，该坐标系中的点用（r，β，ε）表示。

2）传感器笛卡尔坐标系

传感器笛卡尔坐标系是一个空间直角坐标系，其原点位于传感器中心，Y 轴平行于艏艉线，指向舰艏为正，X 轴垂直Y 轴且平行于甲板，指向右舷为正，Z 轴垂直甲板向上。后续用“S-XYZ”代指传感器笛卡尔坐标系，该坐标系中的点用（xs，ys，zs）表示。

3）舰艇甲板坐标系

舰艇甲板坐标系是一个空间直角坐标系，其原点位于舰艇摇摆中心，Y 轴平行于艏艉线，指向舰艏为正，X 轴垂直Y 轴且平行于甲板，指向右舷为正，Z 轴垂直甲板向上。后续用“B-SFU”代指舰艇甲板坐标系，该坐标系中点的坐标用（xb，yb，zb）表示。

4）舰艇地理坐标系

舰艇地理坐标系是一个空间直角坐标系，其原点位于舰艇摇摆中心，X 轴平行于水平面指向正东，Y 轴平行水平面指向正北，Z 轴垂直于水平面向上。后续用“L-ENU”代指舰艇地理坐标系，该坐标系中点的坐标用（xl，yl，zl）表示。

5）地心地固坐标系

地心地固坐标系是一个空间直角坐标系，其原点位于地球中心，Z 轴与地球自转轴相同，指向北极，X-Y 平面位于赤道面，X 轴穿过格林威治子午线，Y 轴与X，Z 构成右手系。后续用“ECEF”代指地心地固坐标系，而该坐标系中点的坐标用（xe，ye，ze）表示。

6）大地坐标系

大地坐标系是大地测量中以参考椭球为基准面建立起来的坐标系，空间点的位置用大地经度L、大地纬度B 和大地高H 表示。后续用“LBH”代指大地坐标系，该坐标系中点的坐标用（L，B，H）表示。

1.2 几种误差定义

从传感器测量到形成最终航迹点，产生影响的主要误差包括：

1）传感器测量误差（δr，δβ，δε）

传感器测量目标的球坐标系误差，可以用（δr，δβ，δε）描述。

2）传感器笛卡尔坐标系对准误差（δφ1，δφ2，δφ3）

该误差指实际传感器笛卡尔坐标系与理论传感器笛卡尔坐标系（理论传感器笛卡尔坐标系应对准舰艇甲板坐标系）的对准误差，可以用实际传感器笛卡尔坐标系相对于舰艇甲板坐标系的3 个误差角（δφ1，δφ2，δφ3）来描述。

3）传感器基线误差（δxb，δyb，δzb）

基线指传感器相对舰艇中心的位移，事先测量以供传感器数据处理时使用，但由于测量仪器误差以及测量后舰艇形变等原因，数据处理中使用的基线包含一定误差，该误差可以用基线在舰艇甲板坐标系中的误差（δxb，δyb，δzb）来描述。

舰艇甲板坐标系是一个非稳定坐标系，不仅随着舰艇平移和转向，还随着舰艇进行摇摆运动，其参考轴的空间方向在不断地变化。这个变化由舰艇上的惯性设备所观测并提供给平台使用，而惯性设备的观测含有误差。该误差可以用舰艇纵摇角、横摇角、航向角误差（δ1，δ2，δ3）来描述。

5）舰艇位置误差（δL，δB，δH）

舰艇位置信息由导航系统提供，该误差可以用导航系统给出的舰艇大地坐标误差（δL，δB，δH）来描述。

1.3 坐标转换误差分析

1）传感器球坐标系到传感器笛卡尔坐标系（DBE→S-XYZ）

传感器球坐标系到传感器笛卡尔坐标系转换公式为

该坐标转换的误差传播公式为

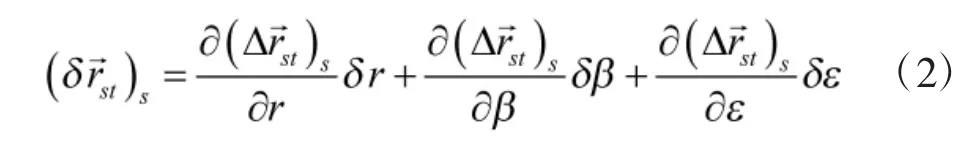
其中，

2）传感器笛卡尔坐标系到舰艇甲板坐标系（S-XYZ→B-SFU）

传感器笛卡尔坐标系到舰艇甲板坐标系坐标转换公式为

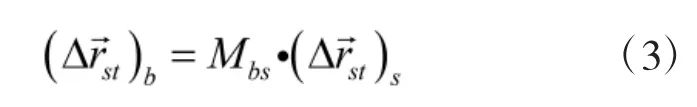
在实际中，（φ1，φ2，φ3）一般未测量（即默认两个坐标系是对准的），因此，这里取（φ1，φ2，φ3）测量值为0。得到误差传播公式为

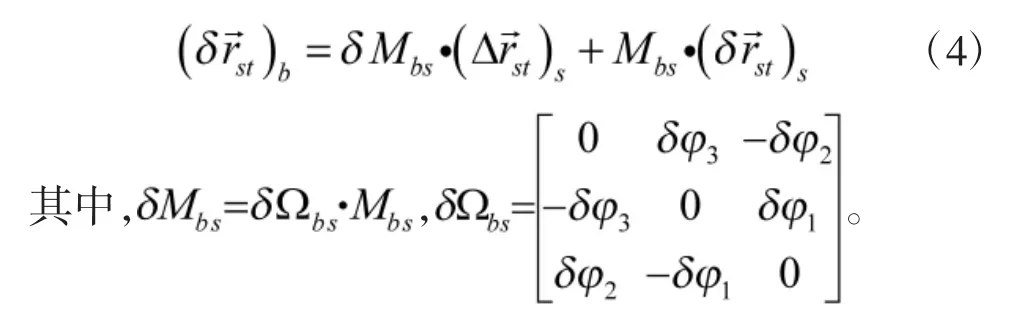
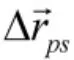
误差传播公式为

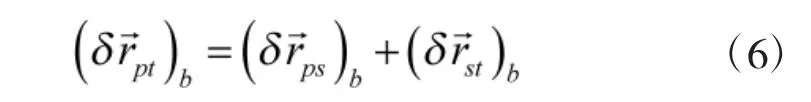
3）舰艇甲板坐标系到舰艇地理坐标系（B-SFU→L-ENU）

舰艇甲板坐标系到舰艇地理坐标系坐标转换公式为

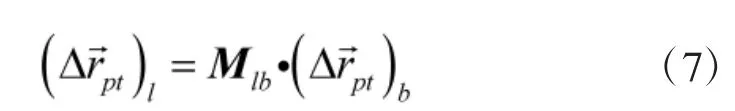
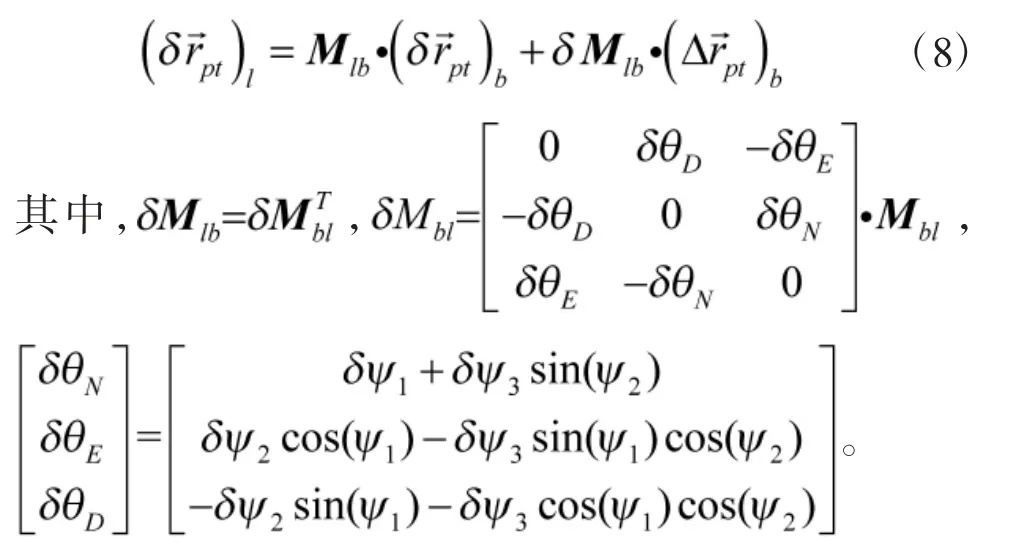
4）舰艇地理坐标系到地心地固坐标系（L-ENU→ECEF）

舰艇地理坐标系到地心地固坐标系坐标转换公式为

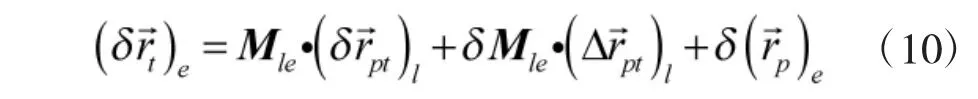
大地坐标系到地心地固坐标系坐标转换公式为

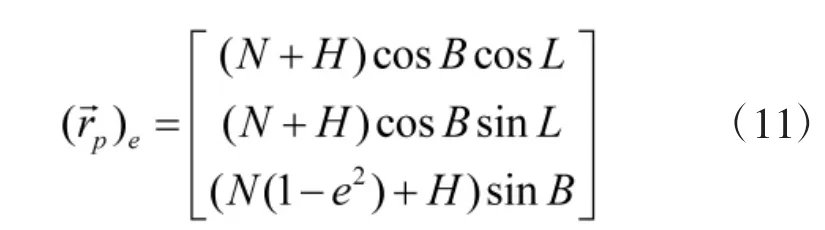
该坐标转换的误差传播公式为：

2 传感器测量误差数据处理过程中累积传播

2.1 传感器测量误差累积传播过程分析

传感器对目标的测量数据处理要考虑1.2 中五类误差的综合作用效果，其处理流程图及其涉及的误差如图2 所示，详细的转换步骤及其误差累积分为如下6 步：

1）第1 步

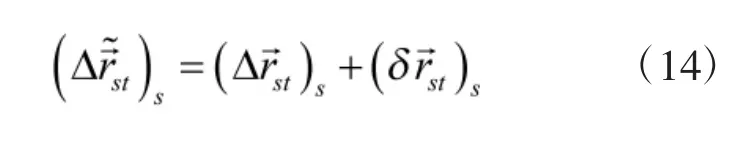
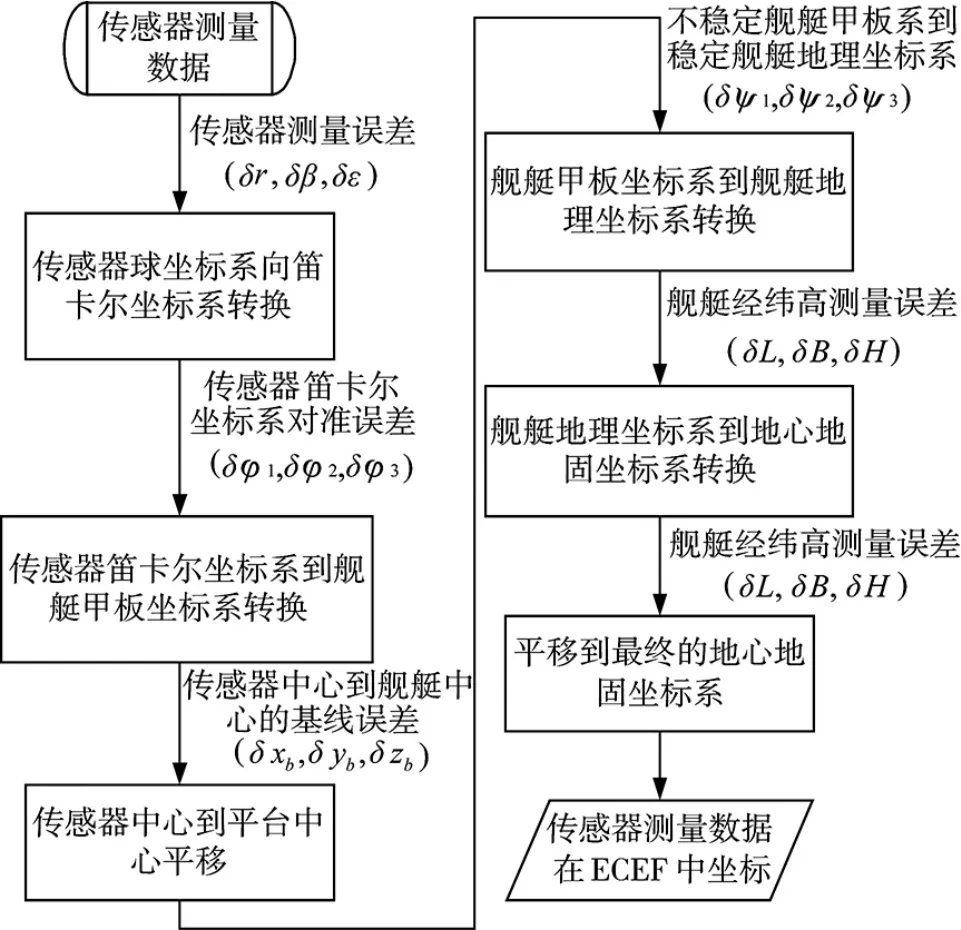
图2 传感器量测到ECEF 坐标系转换过程误差累积

2）第2 步

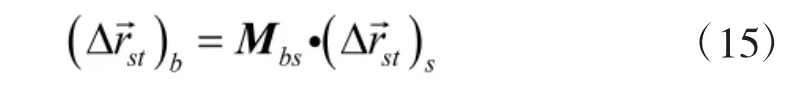
同样，由于传感器的测量以及传感器笛卡尔坐标系的对准都是有误差的，因此

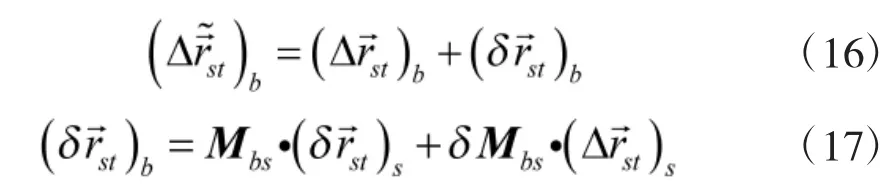
其中

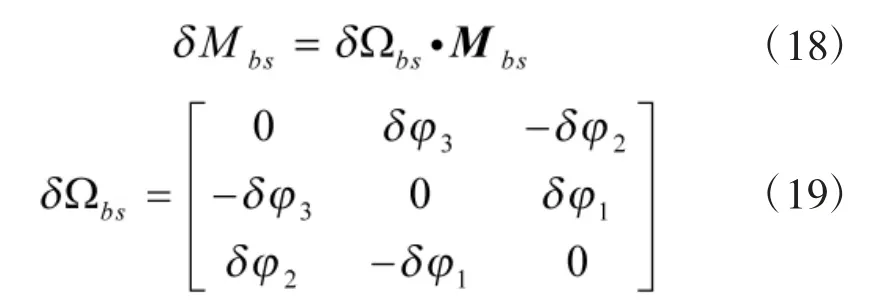
其中，（δφ1，δφ2，δφ3）是传感器笛卡尔坐标系的对准误差。

3）第3 步

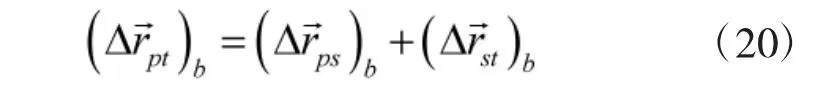
类似地，由于误差的存在

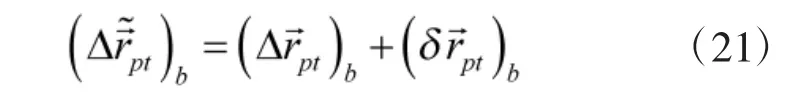
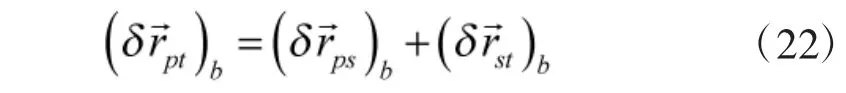
4）第4 步

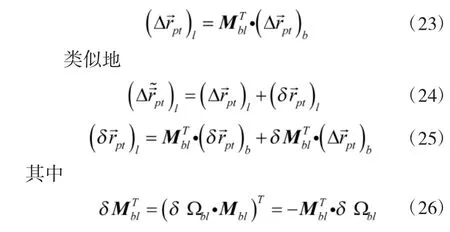
5）第5 步

6）第6 步

2.2 不同测量误差对目标位置估计的影响分析

根据上节综合可得各误差源对目标位置估计的影响为

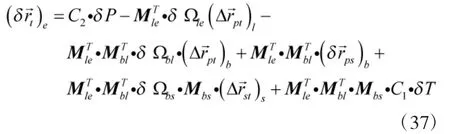
其中，各符号的意义如前节所示。

上述误差的影响都是线性模型，可以很方便地将各误差的影响拆分，如下所示：

平台位置的东向误差δxE对目标位置估计的影响为

平台位置的北向误差δxN对目标位置估计的影响为

平台位置的垂直误差δxD对目标位置估计的影响为

传感器距离测量误差δr 对目标位置估计的影响Sδr为

传感器方位角测量误差δβ 对目标位置估计的影响Sδβ为

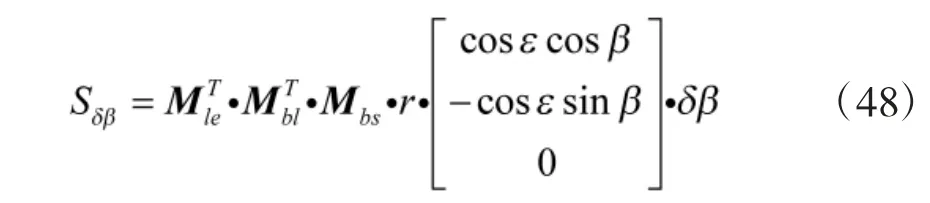
传感器俯仰角测量误差δε 对目标位置估计的影响Sδε为

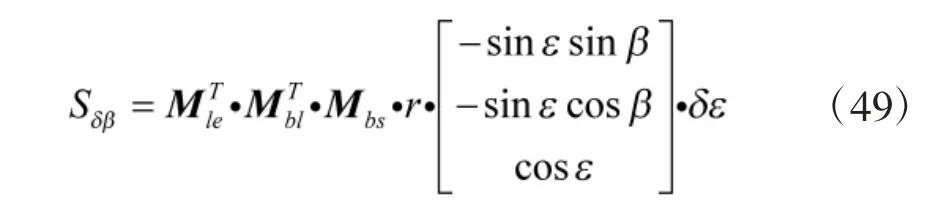
传感器笛卡尔坐标系对准误差δφ1对目标位置估计的影响为

传感器笛卡尔坐标系对准误差δφ2对目标位置估计的影响为

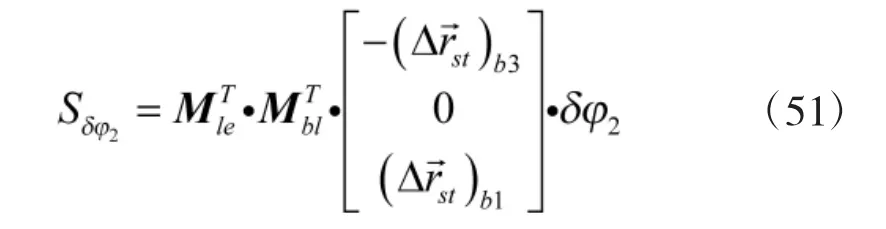
传感器笛卡尔坐标系对准误差δφ3对目标位置估计的影响为

3 仿真结果分析

3.1 误差传播的灵敏度

如果仅仅关注于各误差传播的灵敏度在3 个方向的分量，而不从整体的角度对其进行分析，则很可能丢失关于误差传播的一些重要规律，因为许多误差传播规律往往单独从其分量的传播规律中很难体现出来，只有将各分量综合在一起考虑时才能比较清晰地展现。

定义误差传播的归一灵敏度为：误差传播灵敏度在3 个方向分量的平方和的开方，即

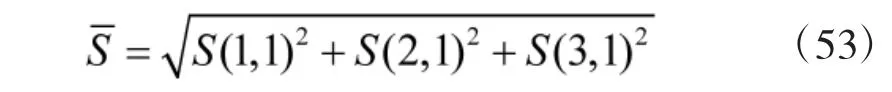
显然，归一灵敏度从整体上描述了一个误差对目标三维空间位置估计的影响。

下面在一些典型的场景下进行仿真。

首先考虑下页表1 所示的场景，仿真结果如表2 所示。再考虑表3 所示的场景，仿真结果如表4 所示。从表2 和表4 可以看出：

1）导航位置/ 传感器基线误差传播的归一灵敏度为1，也就是说，一个单位的平台位置/基线误差只会产生一个单位的目标位置误差；另外还可以发现，平台导航位置/传感器基线误差的归一灵敏度与目标和平台的相对位置无关，是一个常量。

表1 仿真场景1

2）平台姿态、航向误差传播的归一灵敏度和传感器笛卡尔坐标系对准误差传播的归一灵敏度一一对应相等，都是依赖于目标与平台相对位置关系的变化量。

3）传感器距离测量误差传播的归一灵敏度和目标与平台的相对位置无关，等于1；但传感器方位测量误差和俯仰角测量误差的归一灵敏度则和目标到平台的相对位置有关。

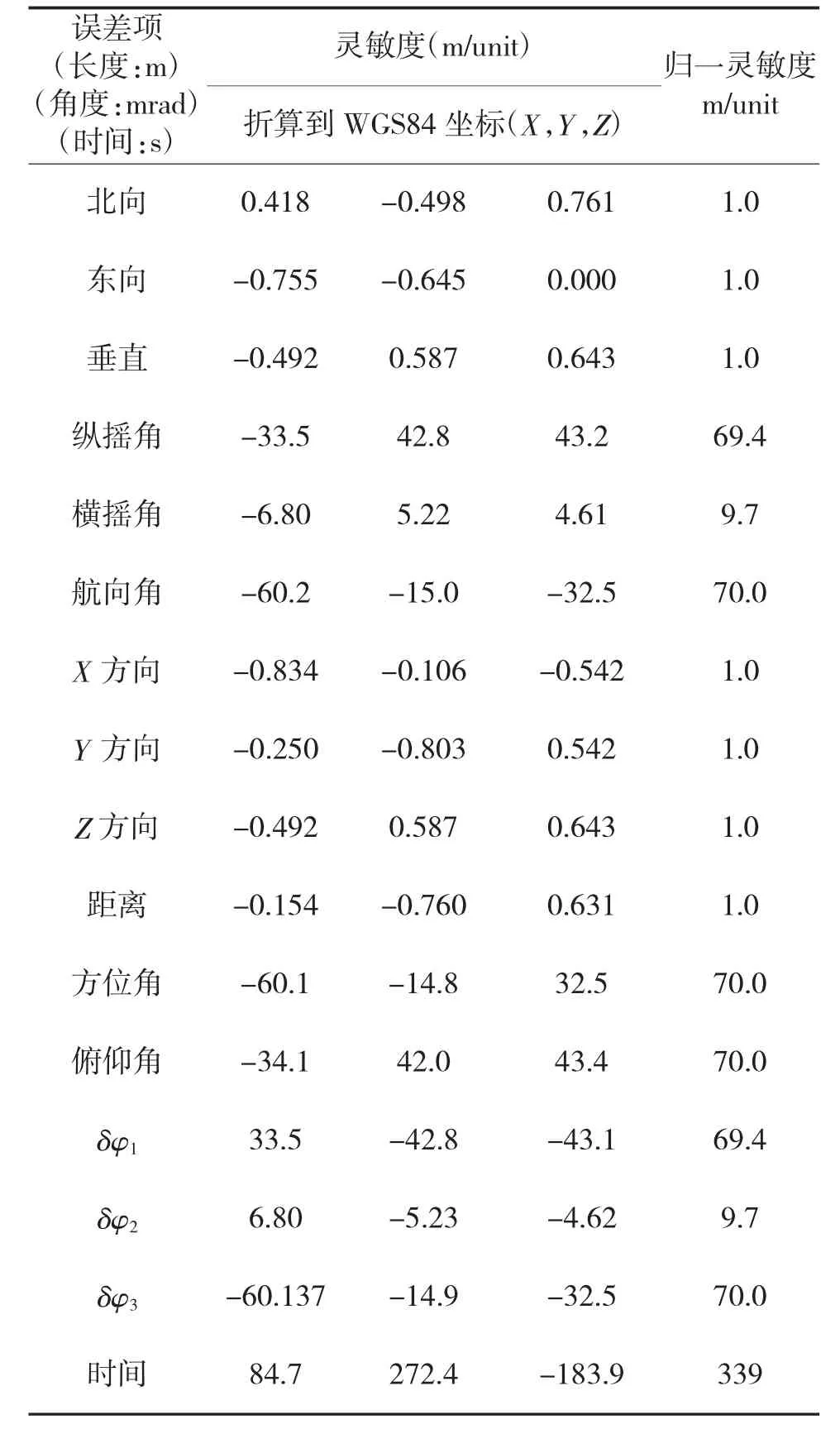
表2 各误差传播的灵敏度（仿真场景1）

4）时间误差传播的归一灵敏度和目标与平台的相对位置无关，只与目标的速度、加速度以及测量测量使用的延迟时间（即需要外推的时间）有关；目标的速度/加速度/测量使用的延迟时间越大，时间误差对目标位置估计的影响越大。

3.2 误差传播灵敏度空间分布

平台导航位置误差、传感器基线误差、传感器距离测量误差以及时间误差传播的归一灵敏度均是一个定值（等于1），和目标与平台的相对位置关系无关；但是，平台姿态航向误差、传感器方位俯仰测量误差和传感器笛卡尔坐标系对准误差的传播的归一灵敏度，则是一个和目标与平台相对位置关系有关的变化量。为了解这几个误差的传播规律，需要考察不同目标-平台相对位置关系下，这些误差传播归一灵敏度的变化情况。

鉴于此，绘制了这些误差传播的归一灵敏度的几何分布图（等值线图），如下页图3（仿真场景1）和图4（仿真场景2）所示，其中红色星号表示的是平台的位置（由于平台姿态航向误差传播的归一灵敏度和传感器笛卡尔坐标系对准误差传播的归一灵敏度是一一对应相等的，所以只绘制了前者的分布图，后者只需参照前者即可）。

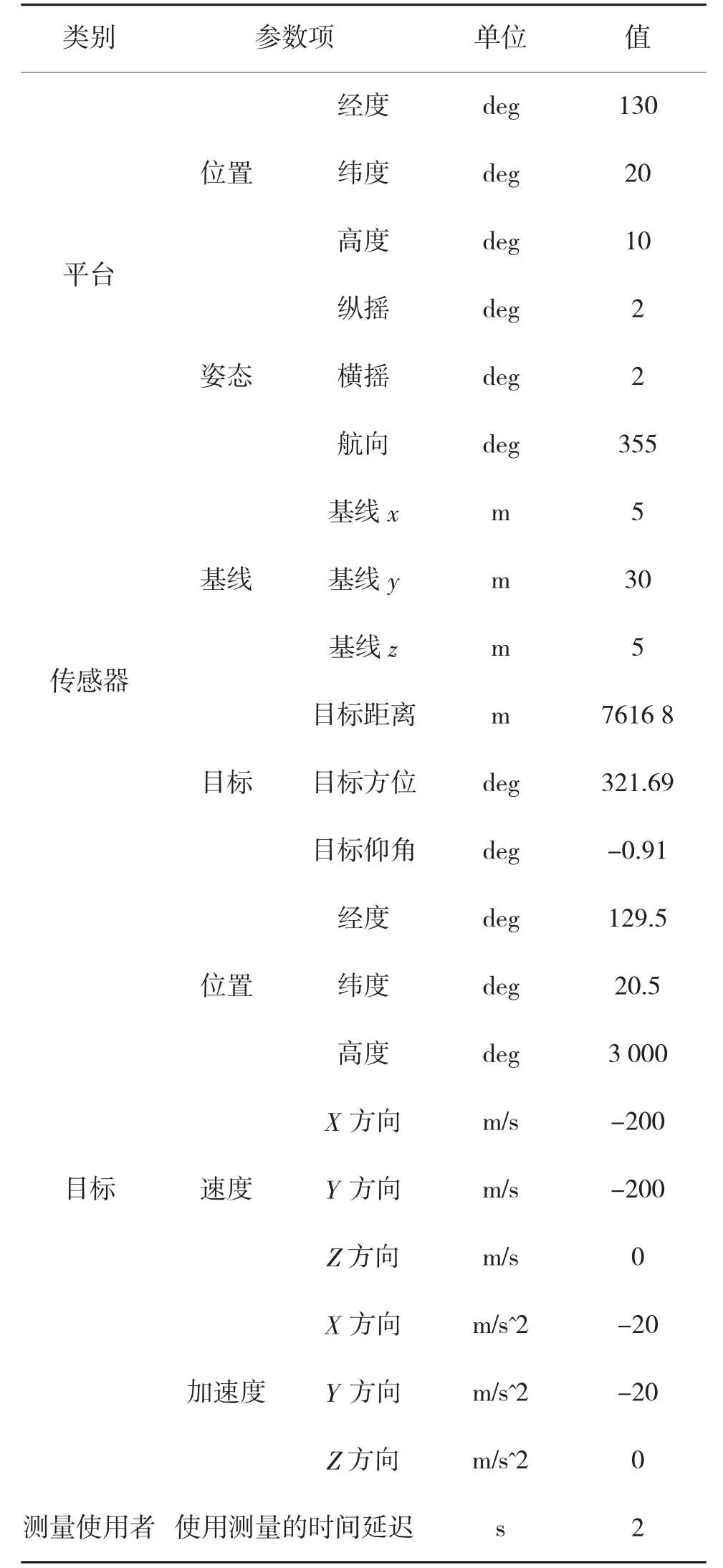
表3 仿真场景2

根据图3 和图4，再结合各误差传播灵敏度的理论表达式不难看出：

1）平台纵摇角误差（传感器笛卡尔坐标系对准误差δφ1）传播的归一灵敏度与目标在舰艇甲板坐标系中Y 方向的距离成正比。

2）平台横摇角误差（传感器笛卡尔坐标系对准误差δφ2）传播的归一灵敏度与目标在舰艇甲板坐标系中X 方向的距离成正比。

表4 各误差传播的灵敏度（仿真场景2）

图3 仿真场景1

3）平台航向角误差（传感器笛卡尔坐标系对准误差δφ3）和传感器方位测量误差传播的归一灵敏度和目标到平台的水平距离成正比。

4）传感器俯仰角测量误差传播的归一灵敏度和目标到平台的距离成正比。

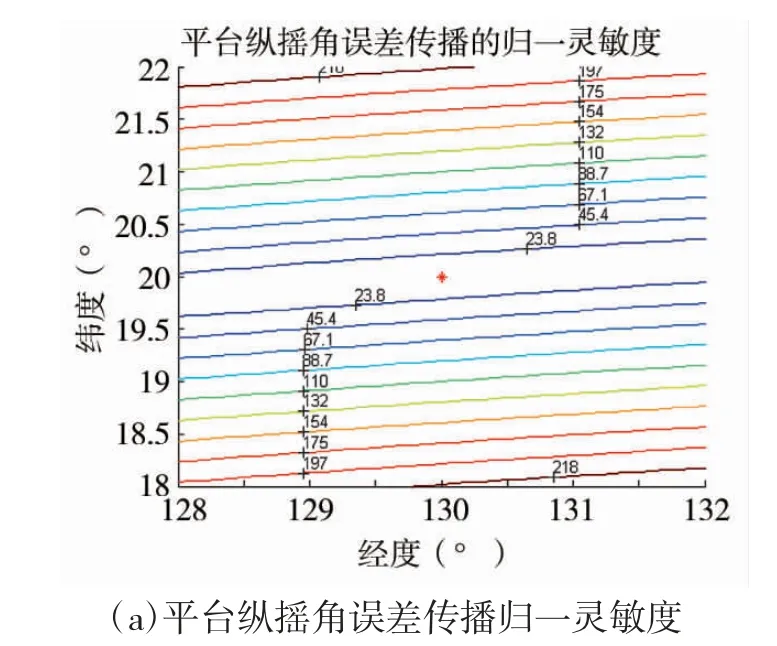
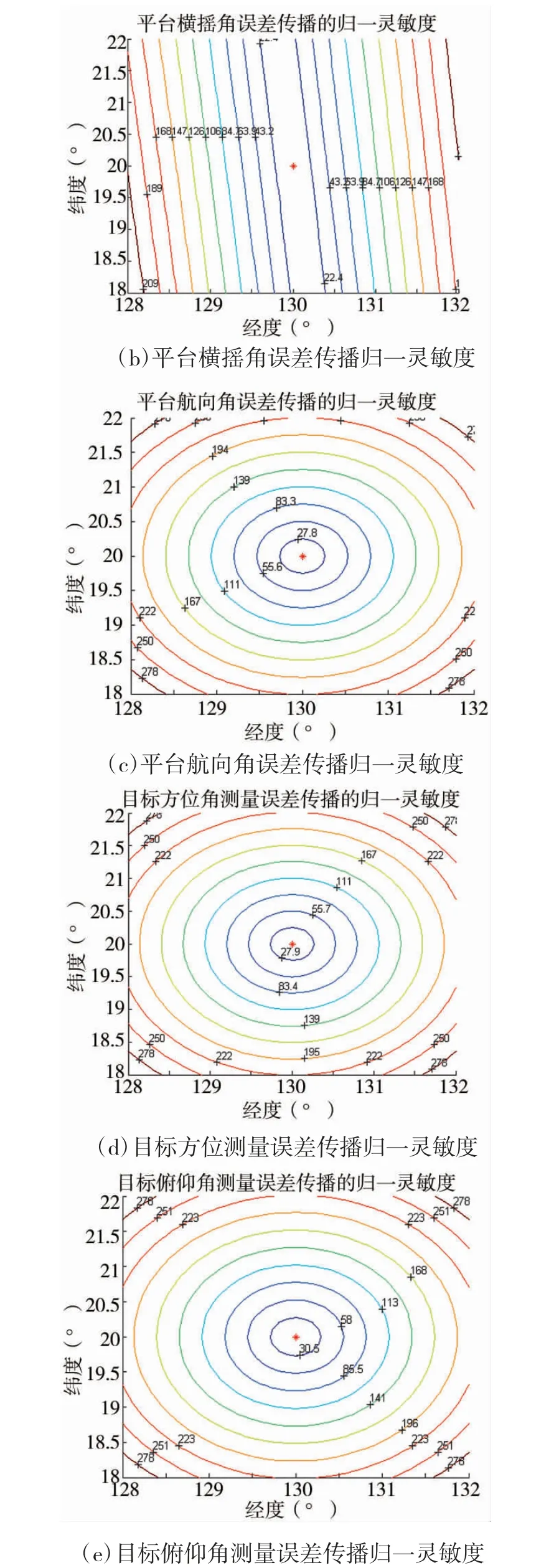
图4 仿真场景2

3.3 目标位置误差源分布

上两节对各误差对目标位置估计的影响作了较为详细的定性分析；本小节从定量的角度对各误差对目标位置估计的影响作详细分析。

首先定义各测量的标准误差水平如表5 所示，并假设各误差是相互独立的。

表5 各测量的标准误差水平表

结合表3 和表4，可以得到标准误差水平条件下各误差对目标位置的影响结果，如图5（仿真场景1）和图6（仿真场景2）所示，其中红色条形的长度代表该误差造成的目标位置误差的标准差的大小。

从图5 和图6 可以看出，在仿真设置的标准误差水平下，目标位置误差主要有3 个误差源：平台导航位置误差，传感器测量误差，时间误差。

4 结论

在多平台多传感器信息融合中，传感器的测量精度是影响统一态势正确形成的一个关键因素。本文采用理论建模并辅之以数字仿真的方法，对分布式系统中，各误差源对传感器测量精度的影响进行了详细的讨论。

首先根据实际情况分析了影响舰载传感器目标测量精度的各项误差。这些误差可以归为三大类：一类是传感器误差，主要包括传感器测量误差和传感器平台的误差；一类是平台导航误差，主要包括平台位置误差和平台姿态航向误差；最后一类是时间误差，包括时戳误差、时间同步误差等等。

图6 仿真场景误差影响2

然后，以误差传播理论为工具，在严格遵从舰载传感器数据处理流程的基础上，推导了各误差到目标航迹点（地心地固坐标系下）的传播模型，并以模型为依托，分析了误差的传播规律，这些传播规律从定性的角度深刻反映了误差的性质。

最后，根据标准误差水平表在一些典型的场景下进行了仿真。仿真显示：平台位置误差、传感器测量误差和时间误差是目标位置误差的3 个主要来源，在文中给定的误差水平下，这3 个误差导致的目标位置误差占整个目标位置误差的80%以上。因此，改善舰载传感器目标航迹质量应主要从这3 个误差着手。

另外，需要指出的是，虽然本文具体给出的是舰载传感器目标测量精度的分析，但从文中分析流程不难看出，本文的分析方法具有一般性，可以用于其他平台传感器目标测量精度的评估。