机动作战中资源冲突消解模型构建及求解策略

张 笋，朱 昱，杨明映，王正元

（火箭军工程大学，西安 710000）

0 引言

在导弹部队机动作战过程中，常会遇到工作调整或意外事件导致无法顺利执行原定计划。而变更工作或处置意外情况，需要调动人员、装备、物资、空间等要素。在此过程中，这些要素因为量值有限，而可能发生无法满足多个工作同时调整或同时处置多个意外事件的情况，意味着有限的资源要素出现了冲突，分析预判和妥善解决这些冲突有助于大力提高导弹部队作战能力。一般而言，采用定性的做法可以直观地解决问题，但应用定量的方法，可以更加科学合理地规划安排作战行动［3］。

本文对导弹部队机动作战过程中可能遭遇的资源冲突事件进行归类，从其定性解决过程中详细分析资源调度利用情况，然后着眼于对冲突事件预测判断，利于提前进行防范的目的，采用数学方法手段消解资源冲突问题［4］。

1 基本概念及背景思路

围绕有效解决制约影响导弹部队作战能力的作战资源冲突问题，首先对作战资源及资源冲突的概念内涵进行明确界定，并确定基本分析研究思路［3，5-8］。

1.1 作战资源的概念

《辞海》对资源一词的定义是：资财的来源，一般指天然的财源。本文研究的对象为作战资源，不仅限于资财的范围。对于特定的导弹部队作战样式而言，根据其作战行动特点和需要，其资源有着十分明确的内涵［9］。结合第2 部分的研究中，对导弹部队机动作战资源定义为：为满足导弹部队遂行机动作战任务需要，投入的人员、经费、物资、装备、时间、空间等要素的集合。

1.2 资源冲突的概念

根据以上定义，针对本文研究目的和导弹部队实施无依托随机发射机动作战的情况，对资源冲突作如下定义：在导弹部队遂行无依托随机发射机动作战过程中，因计划外的突发事件，如车辆故障、道路损坏、遭敌突袭、行动变更、装备故障等情况，而导致原定安排的人员数量P、经费额度C、工具设备数量M、保障车辆数量E、时间安排T、空间数量S等资源使用与计划发生矛盾的现象［10］。

1.3 研究背景目的

实战中，导弹部队的作战行动常常面临着突发特情的干扰和威胁，科学调度应用现有资源，高效快捷地处置特情，是导弹部队顺利完成作战任务的重要前提。对此许多专家学者从不同角度进行了分析研究，提出了相应策略，如文献［1］中，陈进、龚时雨提出了基于智能算法的作战资源优化分配方法，建立了多约束条件的资源分配模型，并用遗传算法进行求解；在工程实践中，类似的问题也被广泛研究，如文献［2］中，齐金平、查显锋提出了多任务多资源优化调度的病毒遗传算法，文中假定的情形与导弹部队实战中面临解决的问题很相似，是一种可供参考借鉴的方法。这些研究的共同特点是根据实际情况建立了数学模型，并用不同的方法进行求解，其中采用智能算法的求解过程较复杂，原理难以被理解，在实践中难以被导弹部队直接应用。因此，本文针对相关人员的研究，立足于导弹部队实际，力图通过定性定量分析相结合，探索一种原理简单、应用方便的解决方案。

具体而言，针对一个执行机动作战任务的导弹导弹部队，在遭遇特情时，必须重点考虑在一定工具设备数量M、人力资源P 和有限的时间T 内，合理安排使用这几类资源，最大程度缩短处置特情的时间，从而确保能把更多的时间应用于具体作战行动［11］。也就是在规定时间T 内，一个导弹导弹部队需要T′就能完成任务，也就意味着若无意外事件，该导弹部队有ΔT＝T-T′的任务富余时间，这个时间就是该导弹部队能用于处置所有特情事件的时间，即在n 个意外事件中，第i 个特情处置的时间为Ti，那么，必须有

本研究的目的是为了实现Tmin，即处置各特情的时间之和最短［12］。

1.4 解决问题的基本思路

首先对影响导弹部队机动作战能力的主要特情（即：冲突事件）进行归类分析，搞清资源调度使用情况及相关制约因素，从定性角度探讨解决方法，理清流程要素和基本特点；在此基础上，将整个作战能力涉及的资源冲突消解看作是一个有统一约束前提的资源调度优化配置问题，求解问题的目的是要在确保作战行动不受影响的前提下，合理安排调度资源解决冲突。解决问题的基本思路是，立足当前导弹部队执行作战任务实际，以面临多特情的复杂情况处置策略为研究对象，理清资源调度、特情处置及时间等元素的数学逻辑关系，建立相应的求解模型，并通过不同策略下模型求解的结果对比，找出消解冲突的最优策略［13-14］。

2 机动作战过程的资源冲突消解策略

2.1 问题特点

基于实战情形的分析，导弹部队作战行动中面临的特情具有3 个鲜明的特点：

一是突发性。从作战准备到作战结束导弹部队归建的全过程各阶段，导弹部队都有可能遭遇特情，且特情发生多数情况下不以主观意志为转移，因而具有难以控制的突发性。

二是多样性。导弹部队的作战行动是一个多部门、多岗位人员、多设备资源在多时间阶段有机协调配合联动的复杂过程，在行动过程中面临的威胁和特情，来自敌、我、环境等各方面，武器装备、资源保障、机动道路等都有可能出现特情影响作战行动，因而具有情形各异的多样性。

三是专业性。各种特情的发生和处置，均涉及某一类专业人员和工具设备，不同类型特情处置通常需要调用具备相应专业技术能力的人员和工具设备，因而具有分工严密的专业性。

2.2 条件设定和数学模型构建

假设执行任务的导弹导弹部队有不同职能分工的特情处置小组P1，P2，…，Pm，共m 个，每个小组具备解决某个特情的专业能力。此外，在多个特情并行发生时能被多次调度使用，参与处置其他非本专业内的特情；每个小组相应的配套有一组工具设备，也即U1，U2，…，Um，共m 组；任务过程中可能应对的特情为S1，S2，…，Sn，共n 个特情；如果每个特情均由最擅长处置该特情的小组去处置，则平均处置时间为t1，t2，…，tn。进一步作如下分析和约定：

1）不同特情工作之间没有先后约束，也就是任意特情Si可能发生在任意时刻；

2）如果处置当前特情的工作小组及工具设备数集合为0，意味着所有的特情小组和工具设备均已经被调用，此时该当前特情需要等待一段时间，等到有空闲小组后再调用于该当前特情处置或者等待处置该特情的最佳小组来处置；

3）每个特情中的一项工作可以根据处置的策略不同交给一个或多个特情小组来共同完成；

4）每个特情都对应有一个最佳处置小组Pm。以独立处置该特情所消耗的时间为衡量标准，即第i个小组Pi处置第K 个特情的为tk，当实现mintk时，则Pi为特情K 的最佳处置小组；

5）出现的特情允许不进行处置，也就是此时有特情替代方案，其结束时间记为tiB；

6）所有特情处置时所需工具器材和人员调用，不考虑调配时间，也就是在策略已定情况下，只要发生特情，导弹部队就按预定策略处置，资源调度时间可忽略不计；

7）考虑每个特情处置时的等待时间，记为tiD，每个特情处置过程与其他特情的交叉重叠时间记为tiR。

根据研究目标，定义数学模型如下：

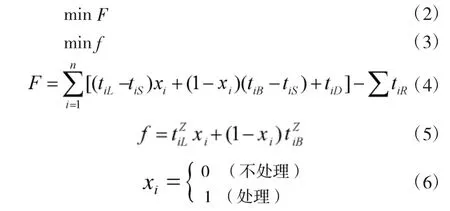
以上模型中：

式（2）中，F 表示处置所有特情消耗的时间之和，即采用不同策略处置完毕所有特情，只有耗时最短的策略才为最优策略。

式（3）中，f 表示处置所有特情中最后一个特情处置完毕的时刻，即采用不同策略时，只有使得处置完毕最后一个特情所处时刻值最小的策略才为最优策略。

式（4）中，tiL、tiS分别表示特情i 的结束、开始时刻，xi为决策变量，tiB表示采用替代方案处置特情i的结束时刻，tiD表示处置特情i 前需要等待的时长，tiR表示处置特情i 时，与处置其他特情的交叉重复时间。

式（6）中，xi取0 时，表示特情i 不作处置，而xi取1 时，表示特情i 需处置。

2.3 消解策略分析

实战中，最复杂的情形是面临同时处置多特情，一般而言，导弹部队会针对特情基于不同策略采取不同的解决方案。常采取的策略一般有如下3 种。

策略1：一次调度分配原则。就是在特情处置决策时明确，对多个特情进行处置，一个职能小组只负责处置本专业类的固定特情，中途不能更换小组和相应的工具设备。也就是当小组Pi负责处置特情K 时，必须从开始到结束全部由Pi完成。其资源特情对应关系如图1 所示。

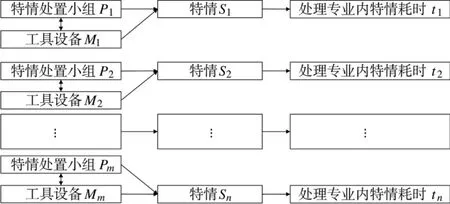
图1 基于一次调度分配的资源特情对应关系

策略2：多次分配调度协作处置原则。就是在特情处置决策时明确，对多个特情进行处置，第i 个职能小组Pi可以根据需要任意调用于接替在处置第k个特情的小组继续处置特情。其逻辑关系如图2 所示，此时难以通过逻辑对应图反应各特情的处置消耗时间。

图2 基于多次分配调度协作处置原则的资源特情对应关系

策略3：重要性优先处置原则。就是方案中明确，在作战行动中对多个特情同时进行处置时，若其中一个特情i 的处置对整个作战行动影响很大，甚至不处置该特情，后续任务无法继续进行，那么，此时必须先处置特情i，然后再按照策略1 或者策略2 进行处置。

3 消解策略应用过程及实例

3.1 过程步骤

具体处置特情时，前述3 个策略的应用，一般是如下两种模式：

模式1：策略3+策略1。即对特情优级判断排序后，应用策略1 处置。

模式2：策略3+策略2。即对特情优级判断排序后，应用策略2 处置。

应用以上两种处置模式的原因是，在实战中，必须首先对遭遇特情的优先级进行判断排序，之后才可以进一步判断要处置的各特情是否有替代方案，在此基础上，才可以选择策略1 或策略2 进行处置。概括起来就是4 个步骤，即：

步骤1：优先级判断。根据所发生的特情对导弹部队行动影响大小判断，影响大的优先级高，必须先对其处置。

步骤2：判断是否用替代方案。以节约时间为最先判断准则，在时间相同的情况下再考虑节约资源成本。具体分析如下：

图3 发生特情i 的处置时间分布

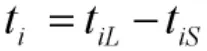
图4 发生特情i 用替代方案处置时间分布

步骤3：资源调度分配。即选择策略模式1 或者策略模式2 处置特情。

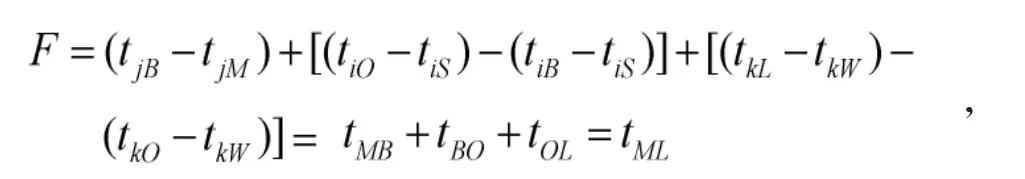
此结果与从时间分布图上得出的结果一致。

图5 3 个特情分布及处置时间情况

3.2 基本流程

根据前面的分析，资源冲突消解策略运用的基本流程如图6 所示。

图6 消解模式策略应用流程

3.3 实例详解

实战中，比较复杂的情形是面临同时处置多特情的情况。为了具体说明模型应用及策略求解过程，这里假设导弹部队同时处置多特情的两种情况，通过不同情况下运用不同策略对模型求解，对比分析两种模式策略的优劣。

情况1：某次作战行动的M 时刻，导弹部队面临处置3 个特情，即：S1、S2、S3，可供调用处置特情的小组为P1、P2、P3，根据整个作战行动安排，处置3 个特情的总时间必须满足：

其中，S1、S2为同一类特情，对应的处置专业小组为P1，P1处置该类特情的平均时间一般为1.5 h，S3对应的处置专业小组为P3，P3处置该类特情的平均时间一般为3 h，P2为其他特情专业小组，其处置当前两类特情的平均时间分别为2.5 h、4 h。3 个特情的优先级为S3>S1=S2，经评估3 个特情替代方案耗时分别为：3 h、3 h、3.5 h。具体条件设定如表1 所示。

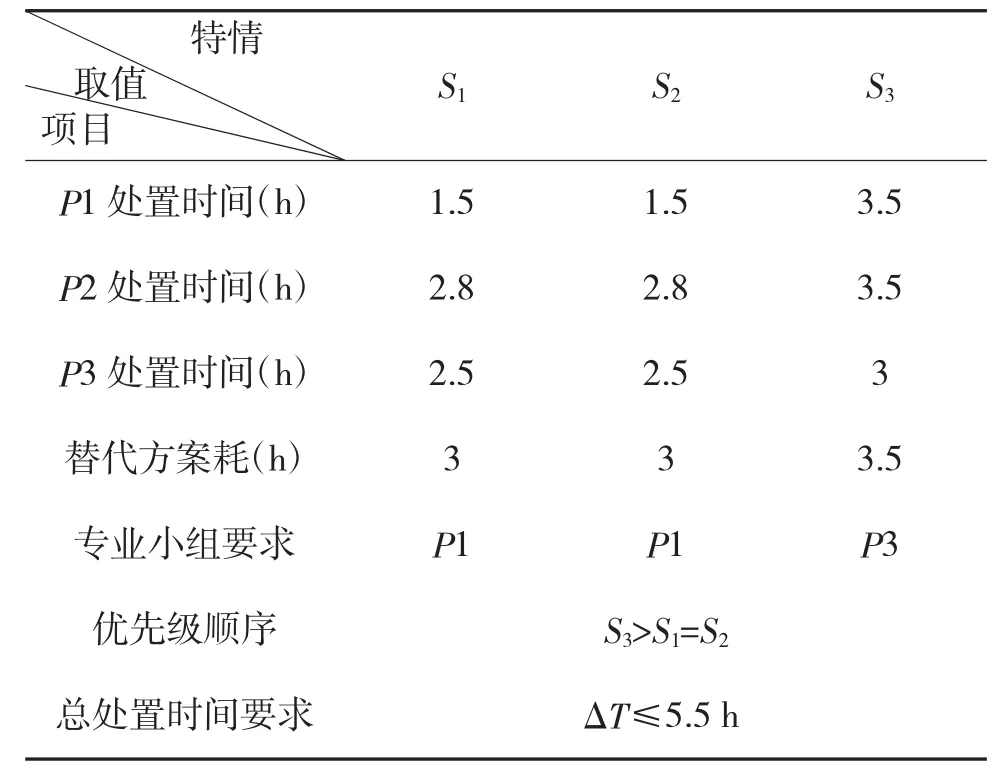
表1 导弹部队k 时刻遭遇特情S1、S2、S3 的参数统计表

分别运用两种模式策略来求解模型，过程如下：

模式1：策略3+策略1。

步骤1：优先级判断。由设定条件可知必须先处置S3，再处置S1、S2。

步骤2：判断是否用替代方案。由设定可知，替代方案耗时过长，不能使用，各特情均必须处置，也即xi=1。

步骤3：资源调度分配。由表1 及求解目标可知，应将P1分配于处置S1或S2，P3分配于处置S3，因为S1、S3同时调用P1发生冲突，因此，根据本模式策略，只能将P2分配于处置S1、S2中一个，假定调用P2来处置S2，则资源调用分配情况如表2 所示。

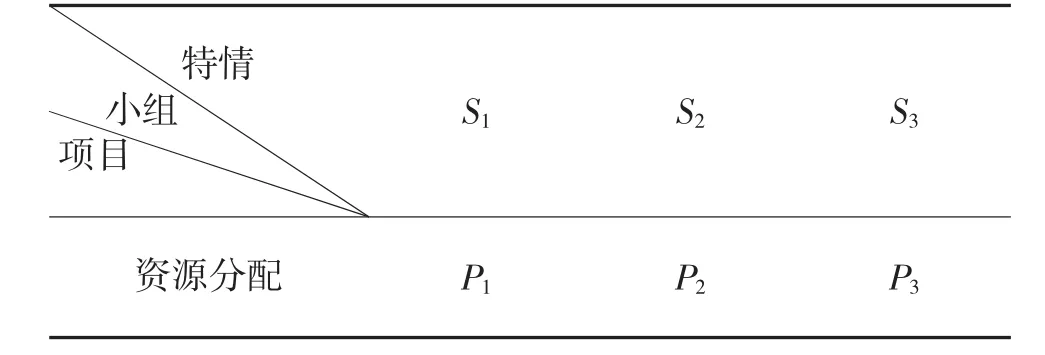
表2 模式1 处置特情S1、S2、S3 的资源分配计划表

步骤4：模型计算求解。根据各特情优先级情况和各小组处置各特情的时间进度，具体分布情况如图7 所示。

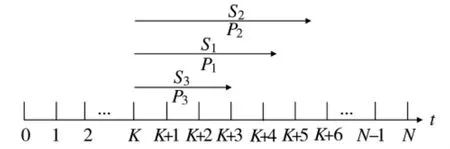
图7 用模式1 策略处置特情的时间进度情况

根据图7，利用2.2 节中的模式公式，可求得F=5.8 h，f=K+5.8 h，因总处置时间5.8 h>ΔT，可见此种模式策略下，无法在规定时间内处置完毕特情事件。

模式2：策略3+策略2。

步骤1、步骤2 内容与模式1 一致。

步骤3：资源调度分配。在模式1 步骤3 分析基础上，针对S1、S2同时调用P1发生冲突，按照模式2策略安排，将P1先分配于处置S1，P2先分配于处置S2，P3分配于处置S3，由表1 可知，在P1处置完毕S1后，P2未处置完成S2，此时再调用P1接替P2处置S2，则此时的资源调用分配情况如表3 所示。

表3 模式1 处置特情S1、S2、S3 的资源分配计划表

步骤4：模型计算求解。根据各特情优先级情况和各小组处置各特情的时间进度，具体分布情况如图8 所示。

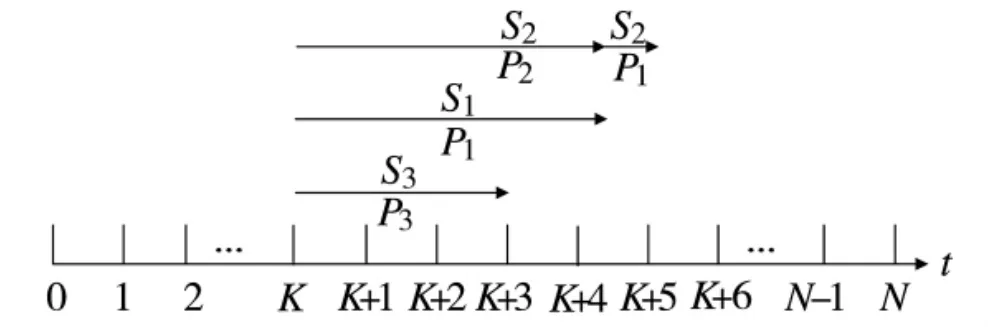
图8 用模式2 策略处置特情的时间进度情况

根据图8，利用2.2 节中的模式公式，可求得F=5.2 h，f=K+5.2 h，因总处置时间5.2 h<ΔT，可见此种模式策略下，按照规定时间处置完毕所有特情事件。

比较两种模式，式（2）min F=5.2 h，式（3）min f=K+5.2 h，可见模式2 优于模式1，此种情况应该选用模式2：策略3+策略2。

情况2：某次作战行动的K 时刻，导弹部队同时面临处置2 个特情S1、S2，可供调用的处置小组为P1、P2，在K+1 h、K+2 h 时刻又分别面临处置2 个特情S3、S4，可供调度使用的处置小组为P3、P4。且S1、S3为同一类特情，其对应专业特情小组为P1，S2、S4分别对应的专业特情小组为P2、P4，其他条件设定如表4 所示。

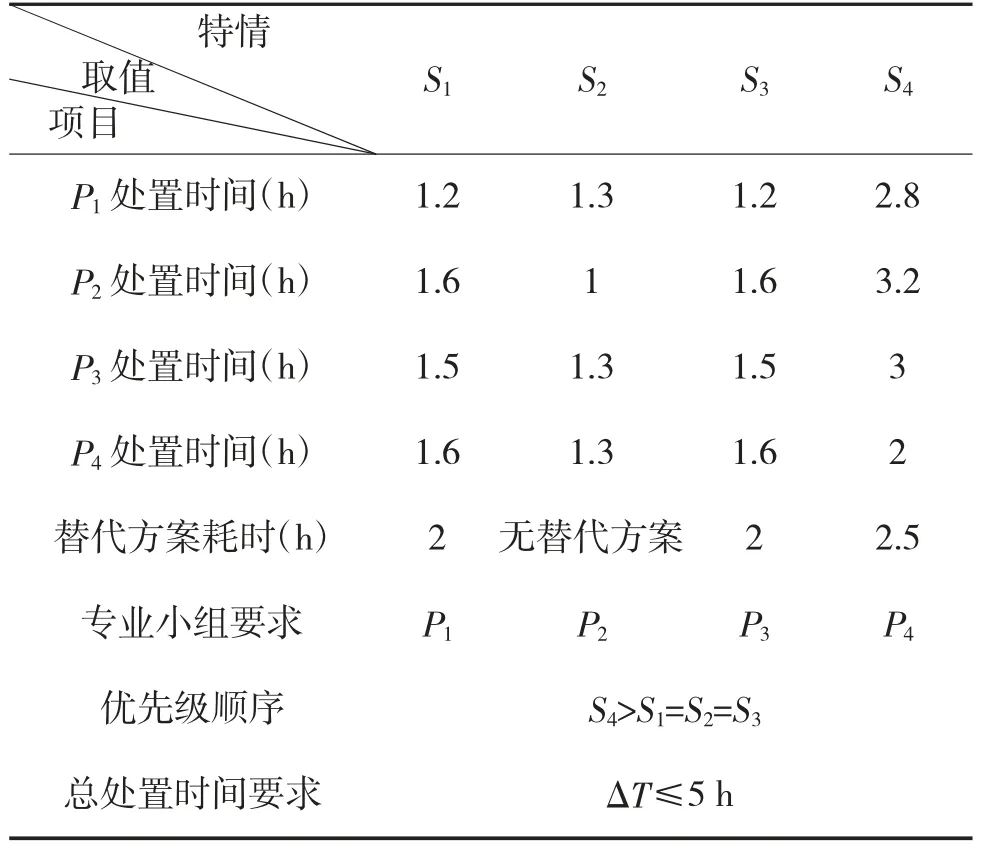
表4 导弹部队k、k+1、k+2 时刻遭遇特情参数统计表

分别运用两种模式策略求解模型。步骤1 和步骤2 过程及情况判断相同，即根据优先级顺序，应优先处置S4，但是因为其最后发生，因此，先对S1、S2、S3进行处置，待S4发生时优先处置，待其处置完毕后，再继续处置其他特情。同时根据设定情况，替代方案均不可用，各特情必须处置，即xi=1。进一步处置过程如下：

模式1：策略3+策略1。

步骤3：根据特情发生时刻进行资源调用分配。

在K 时刻，将P1分配于处置S1，P2分配于处置S2。

在K+1 时刻，此时发生S3，出现最佳资源P1调用冲突，可供调用的小组为P2、P3、P4，根据表4，应选择P3来处置S3。

在K+2 时刻，此时发生S4，只有S3占用了P3，应将P4分配于处置S4；因为优先级S4>S3，因此，S3须暂停等待，待S4处置完毕之后才能继续处置。资源调用分配情况如表5 所示。

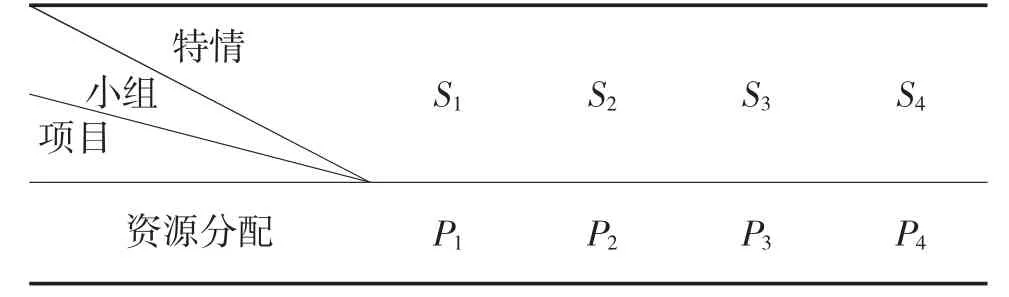
表5 模式1 处置特情S1、S2、S3、S4 的资源分配计划表

步骤4：根据步骤3 的分析，可得到各时刻处置特情的时间进度，具体分布情况如图9 所示。

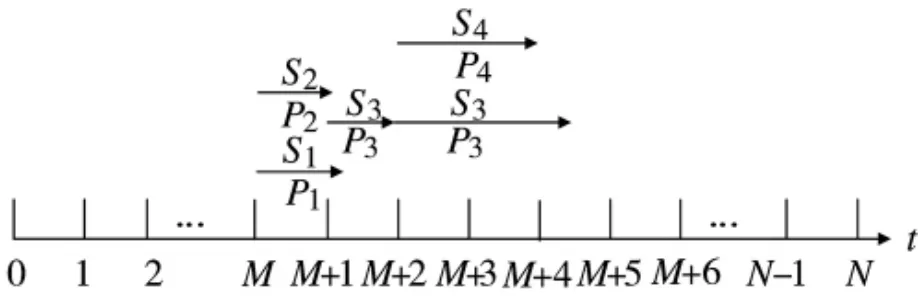
图9 用模式1 策略处置4 个特情的时间进度情况

根据图9，利用2.2 节中的模式公式，可求得F=4.5 h，f=M+4.5 h，因总处置时间4.5 h<ΔT，可见此种模式策略下，在规定时间内处置了所有特情事件。

模式2：策略3+策略2。

步骤3：根据特情发生时刻进行资源调用分配。

在K 时刻、K+1 时刻，资源调用分配与模式1相同。

在K+2 时刻，此时发生S4，只有S3占用了P3，应将P4分配于处置S4；因为优先级S4>S3，因此，S3须暂停等待，待S4处置完毕后才能继续处置。此时须看到，在S4处置完毕后，S3继续处置时可供调用4 个小组均可调用，为加快进度，根据表4，调用P1来接替P3。资源调用分配情况如表6 所示。

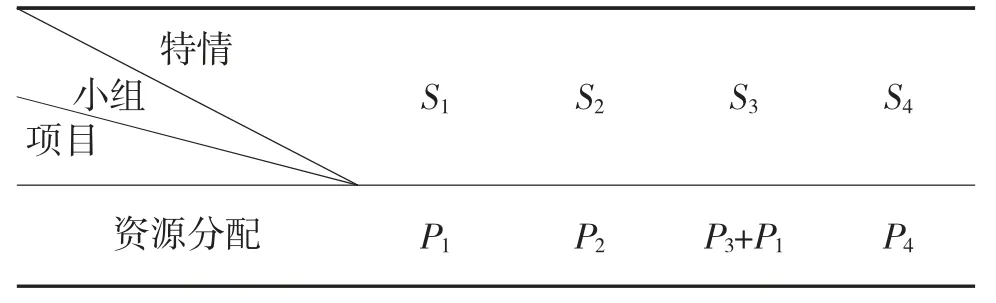
表6 模式2 处置特情S1、S2、S3、S4 的资源分配计划表

步骤4：根据步骤3 的分析，可得到各时刻处置特情的时间进度，具体分布情况如图10 所示。

图10 用模式2 策略处置4 个特情的时间进度情况

根据图10，利用2.2 节中的模式公式，可求得F=4.4 h，f=M+4.4 h，因总处置时间4.4 h<ΔT，可见此种模式策略下，在规定时间内处置了所有特情事件。

比较两种模式，式（2）min F=4.4 h，式（3）min f=M+4.4 h，可见模式2 优于模式1，此种情况应该选用模式2：策略3+策略2。

比较两种情况可知，无论是在同时发生多特情还是不同时刻发生多特情的情况下，利用模式2 的策略调用分配资源进行特情处置和消减资源冲突，最终的时间效果均优于模式1。因此，在实际作战过程中，应该避免一次把人员、工具设备等资源直接固定，而应该针对不同特情的优先级情况、对应的专业人员和工具设备，灵活调度。

4 结论

本文立足于解决影响导弹部队遂行机动作战任务的意外因素，对可能遇到各类突发情况及处置流程进行了梳理，根据有限的人力、工具设备和时间等，围绕最优化调动使用资源，合理解决冲突事件，构建了合理的数学模型。通过综合考虑，引入不同的策略进行分析，最终找到了较优的处置策略，为导弹部队在实际作战行动中有效应对此类问题提供了有益参考借鉴。