光幕靶破片速度测量方法及误差分析*
禄晓飞,易成龙,邹卫科,涂国勇,杨红兵
(1.酒泉卫星发射中心,甘肃 兰州 732750;2西安卫星测控中心,陕西 西安 710043)
0 引言
破片是毁伤的重要手段之一,破片的主要杀伤手段来自于自身的动能,因此精确可靠的破片速度是武器总体计算引战配合和杀伤概率时的必要参数,是衡量武器系统的一项重要指标,也是评估毁伤能力的重要依据。光幕靶测速系统通过记录破片飞过光幕的时间和距离计算其着靶速度,本文设计并实现了破片速度测量方案及数据处理方法,并研究了破片速度误差的精确计算方法[1-6]。
1 速度测量原理
光幕靶测速原理如图1所示[7-10]。当破片穿过光幕时,遮住了进入探测器阵列的部分光线,光电探测器阵列接收到的光通量发生变化,光幕就相应产生一个触发信号。破片飞过两光幕的时间t1和t2,那么破片通过光幕靶的时间为:t=t2-t1。当破片穿过2块定向屏后,可以得到在定向屏1上的穿孔坐标为P1(x1,y1)和定向屏2上的穿孔坐标为P2(x2,y2)。在已知两定向屏的间距为h1和两光幕的间距为h2后,可以得到破片飞行的实际距离为破片穿过2个光幕的平均速度为

图1 光幕靶测速示意图Fig.1 Diagram of measuring velocity by light curtain
v=S/t.
2 着靶信号波形匹配
爆炸后,破片飞散有可能出现较为集中的现象,导致同一个光幕靶接收到了多个破片,此时光幕记录的时间信息、定向屏上的穿孔会出现多组,如何对时间、位置信息进行准确的匹配,是计算破片着靶速度的关键[11-12]。
破片穿过双光幕的时间是通过光电探测器阵列接收到的光通量变化信号来提取的,由于在实际任务中,飞入同一光幕的破片可能有多个,而且爆炸后环境变化较大,光通量变化杂乱,对破片挡光信号造成了很多干扰。通过对实际任务得到的测时信号进行分析,提出了较为有效的测时信号匹配方法。
图2为试验中某个光幕靶接收到的时间信息,其中红色代表了起始光幕的信号,蓝色代表了截止光幕的信号。这组光幕靶在任务中实际接收到的破片为5个,但是产生的时间信号却不止5组。可以看到,由于通过光幕的破片较多,受到外界环境因素的影响,光幕接收到的挡光信号很多。可以肯定这其中很大一部分挡光信号并不是预置破片本身造成的,这对提取破片飞过光幕的时间信息造成了很大的干扰。通过将对时间轴进行放大,逐个对光幕靶的时间信号进行了分析,下面通过几种典型和复杂的时间信号对起始、截止信号的匹配准则进行了研究。

图2 某光幕靶时间信号Fig.2 Time signal of light curtain target
2.1 典型时间信号
通过对信号的时间轴进行放大,截取信号中0~0.3 ms的数据,如图3所示。
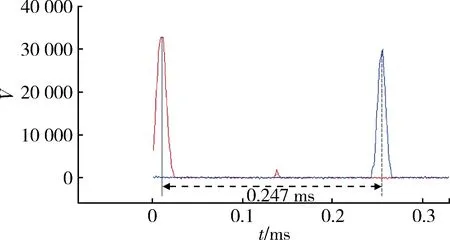
图3 典型时间信号(0~0.3 ms)Fig.3 Typical time signal (0~0.3 ms)
可以看到,这一组信号由一个起始信号和一个截止信号构成,是非常标准的预置破片穿过光幕后产生的挡光信号,计算时间间隔为0.247 ms。其主要特征有:
(1) 信号的最高电压值接近30 000个单位;
(2) 波形为标准的尖峰,两组信号波形一致。
对上述特征可以有如下几点分析:
对于形状、大小均一致的预置破片来说,穿过光幕时挡光的物理过程区别不大,那么其他预置破片穿过光幕所产生的电压值也应该接近30 000个单位,低于此标准过多的信号可以认为不是破片造成的。
预置破片为规则的球形,穿过光幕时挡光强度应该是对称的,所以波形应为对称的尖峰,且两光幕的波形应有较强的一致性。
以光幕的间隔作为破片飞行距离计算,那么破片速度粗略估计与理论计算估计值比较符合。对于入射到同一光幕靶的破片来说,预置破片的速度应该基本上一致,而非预置破片应该略小于预置破片,因此可以认为穿过此光幕靶的其他预置破片的挡光时间间隔也应该在0.2 ms左右。
2.2 复杂时间信号
(1) 相似波形的信号
图4为原时间信号中8~9 ms的数据。
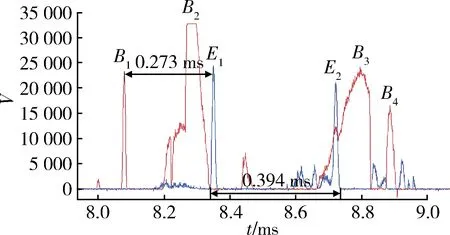
图4 复杂时间信号(8~9 ms)Fig.4 Complex time signal (8~9 ms)
从图4可以看到,电压强度接近30 000个单位的起始信号有4个B1,B2,B3,B4,截止信号有2个E1和E2。其中B1与E1这一组信号形状为标准的对称尖峰,两信号的峰值强度均在25 000左右,间隔为0.273 ms,这些特征与前面的典型时间信号一致,因此可以判断为同一个预置破片的时间信号。
B2与E2其波形虽在大小尺度上有区别,但是波形走向趋势一致,前端都有小幅的振荡,其时间间隔为0.394 ms,速度略小于预置破片,符合实际情况,可以判断为形状不规则的非预置破片穿过光幕时形成的时间信号。
起始信号B3和B4与后续的截止信号时间间隔过短,且后续的截止信号强度过小,不符合破片挡光的实际情况,因此无法匹配,认为是其他因素对光幕产生影响造成的干扰信号。
(2) 对称波形的信号
通过将时间轴放大,在后续时间段落找到了另外一组复杂的波形信号,如图5所示。
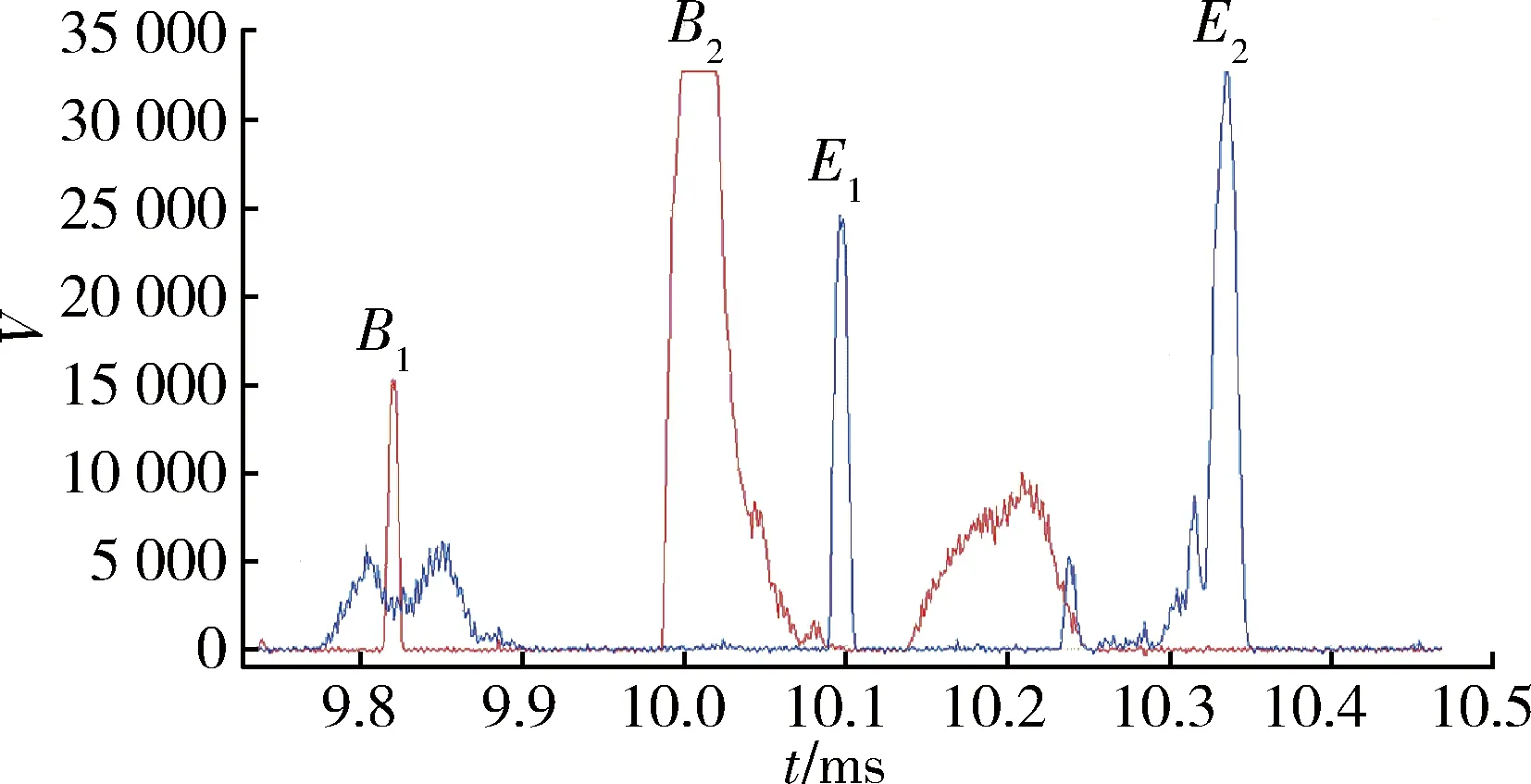
图5 对称信号Fig.5 Symmetric signal
可以看到,有两组时间信号可以匹配,其中B1和E1为一组典型的预置破片挡光信号;B2和E2这一组挡光信号比较特殊,他们的波形图像是对称的,应该为非预置破片在穿过两光幕时发生了翻转造成的。
2.3 测时信号匹配准则
通过对典型和复杂信号的分析,确立了时间信号的匹配准则:
(1) 信号峰值需达到一定强度,强度大小根据设备和破片的状态而定,通常要求在30 000个单位左右;
(2) 信号形状需能够匹配,预置破片的信号波形通常为标准尖峰,非预置破片的波形形状应一致或对称;
(3) 同一光幕靶的破片挡光时间间隔需在理论估算范围内。
3 时间提取准则
在对破片穿过光幕的挡光信号进行匹配后,要想精准地找到破片穿过光幕的时间,需要准确地提取破片通过2个光幕的时刻。通过对几种不同波形的信号进行分析,确立了3种不同的提取准则[13-14]。
(1) 取信号峰值点
对于球形的预置破片来说,由于形状规则挡光信号通常均为标准的尖峰。此种情况信号的峰值时刻点就是破片质心到达光幕的时刻,因此提取峰值点做差即可得到破片质心穿过2个光幕的时间间隔,如图6所示。
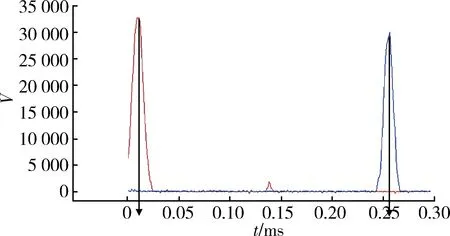
图6 提取信号峰值Fig.6 Extracting signal peak
(2) 取信号的特征点
由于光幕靶的信号接受装置对信号的强度会有截断,因此对于一些造成挡光信号过大,峰值被截断的信号来说无法判断峰值点的具体位置,此时若信号的形状一致,可以提取信号相同的特征时刻点。
例如图7中的B2和E2这一组挡光信号,B2的挡光信号强度过大而被设备截断,无法判断峰值的具体时刻点,因此这里提取破片离开光幕的时刻。

图7 提取信号特征点Fig.7 Extracting signal characteristics
(3) 取信号宽度的中间点
在挡光信号对称时,由于破片在穿过两光幕的过程中发生了翻转,因此峰值点及其他特征点均不能准确的反映破片穿过光幕的时间,此时取整个信号波形进行对称变换后的不动点作为时刻点,也即波形的中间时刻点。
例如图8中的B2和E2这一组挡光信号,B2和E2的挡光信号是对称的,B2的波形起始时刻对应了E2的波形结束时刻,若取这2个时刻点必然导致破片穿过光幕的时间计算过大,造成误差过大,因此这里取波形的中间点。
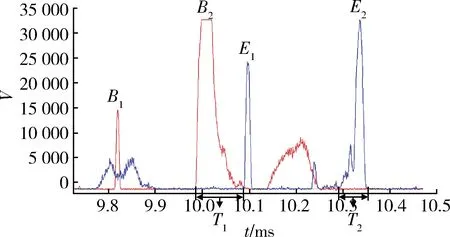
图8 提取信号中间点Fig.8 Extracting signal mid point
对于波形完整且容易判断起始时间的任何波形,此方法均适用。
4 着靶轨迹匹配
为得到破片穿过光幕的距离,主要通过计算破片穿过平行于光幕的定向屏的距离来得到。当多个破片进入光幕靶时,2个定向屏上均保留了多个破片的穿孔,如何将同一破片造成的2个穿孔进行匹配是能否精确计算破片飞行速度的关键。本文通过结合实际任务情况以及破片飞行的空间模型提出了形状匹配和入射角匹配方法。
4.1 形状匹配准则
定向屏的材质为硬质纸板,而破片通常为高速运动的金属,具有极大的动能,在穿透定向屏时,可以认为破片的基本形状不发生改变,因此破片穿透定向屏时留下的穿孔形状应该保持一致,这是在对定向屏上的穿孔进行匹配时的第一条匹配准则。
破片穿过定向屏后留下的穿孔的示意图如图9所示。
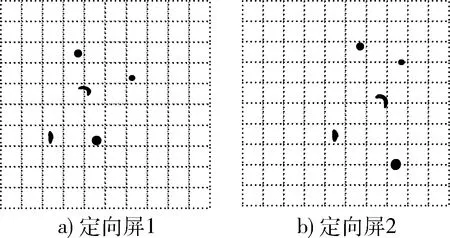
图9 破片穿孔示意图Fig.9 Diagram of fragment perforation
通过图9可以看到,对于2个定向屏上的楔形和月牙形破片可以快速的进行匹配,对于圆形通孔则还需要进一步更精确的算法进行匹配。
4.2 入射角匹配
形状匹配通常只能对形状各异的破片穿孔进行匹配,对于预置的钨珠破片其穿孔为规则的圆形孔,需要更加精确的匹配方法。考虑到入射光幕靶上的破片均是来自于同一爆心,而对于空爆试验来说,破片从爆心飞散到光幕靶的过程可以认为是沿直线运动的,因此建立了破片入射到光幕靶的空间模型,如图10所示。

图10 破片入射光幕靶模型Fig.10 Model of fragment penetrating light screens
通过建立破片入射光幕靶的模型可以看到,爆心O、定向屏1的穿孔A和定向屏2的穿孔B,3点应在同一直线上。这样当已知爆心位置O和定向屏1上的穿孔A的位置时,就可以计算出定向屏2上穿孔B的理论位置。另外,由于爆炸体自身是有一定体积的,并且实际爆心的测量位置是存在一定误差的,所以破片的实际初始位置应在以爆心为中心,半径为r的一个球体范围内。这样在计算得到穿孔B的理论位置后,以B为圆心可以找到一个匹配范围,认为落在此范围内的破片穿孔可以与定向屏1上的穿孔A相匹配。若匹配范围内无合适的穿孔,则认为穿孔A不是由爆心飞来的破片所造成的。
对于定向屏1上的多个穿孔,在计算各自的匹配范围时,由于光幕靶的自身尺寸远小于于爆心到光幕靶的距离,因此可以认为多个破片入射到同一光幕靶时,其由实际爆心位置入射到光幕靶的角度是相同的。因此从另一个角度来看,对于某一个光幕靶来说,只有在定向屏1和定向屏2上的两破片穿孔所成直线满足破片入射到此光幕靶的角度条件时,才可以进行匹配,所以此方法称入射角匹配。
图9的定向屏穿孔情况如表1,表2所示。
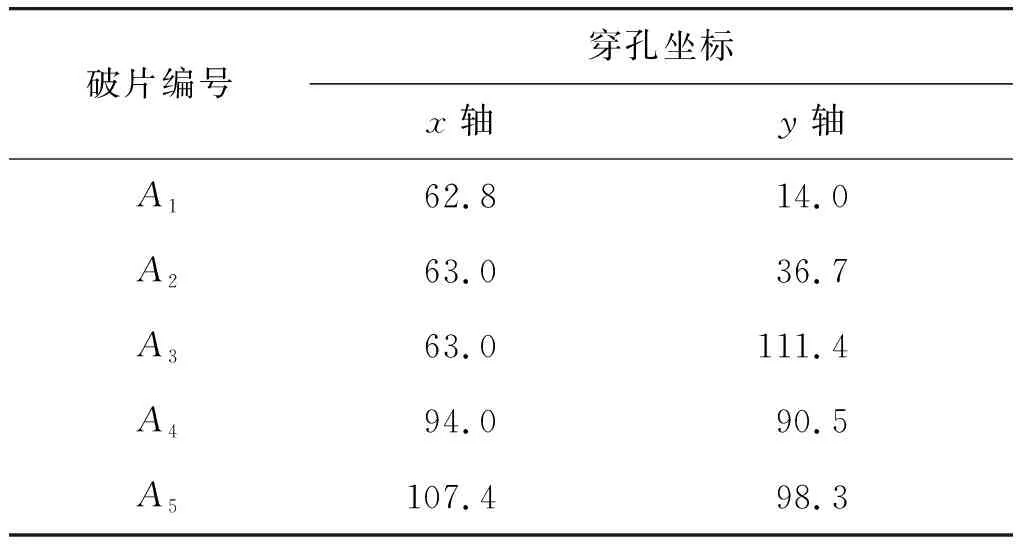
表1 定向屏1上的穿孔坐标Table 1 Perforation coordinates on screen 1
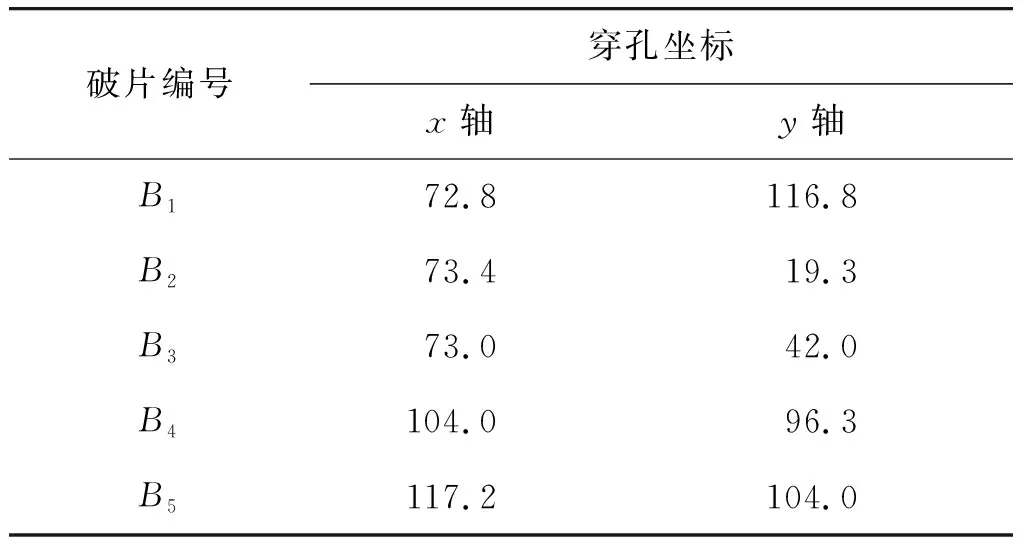
表2 定向屏2上的穿孔坐标Table 2 Perforation coordinates on screen 2
根据入射角可以对两定向屏上的穿孔进行匹配,如表3所示。

表3 匹配结果Table 3 Perforation matching results
5 误差传递模型
破片速度测量的误差主要来自s和t的随机误差,由速度的计算公式可以求得随机误差传递公式:
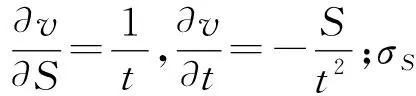
由于随机误差和匹配误差是完全独立的,因此可以认为速度的最终总误差为
σ=σv+vλ.
6 随机误差计算
6.1 测时随机误差
由于挡光信号的波形是具有一定宽度的,那么在计算破片飞过光幕的时间时,对起始信号和截止信号的具体时刻点的选取就决定了时间t的最终精确程度。利用一对起始和截止信号为例,在不同的特征点上提取穿透时间进行了统计分析,最终利用标准差的无偏估计作为测时随机误差[15-17]。
如图2所示,分别对起始信号和截止信号的0,5 000,10 000和峰值4个位置的7组时刻点进行了提取,结果如表4所示。
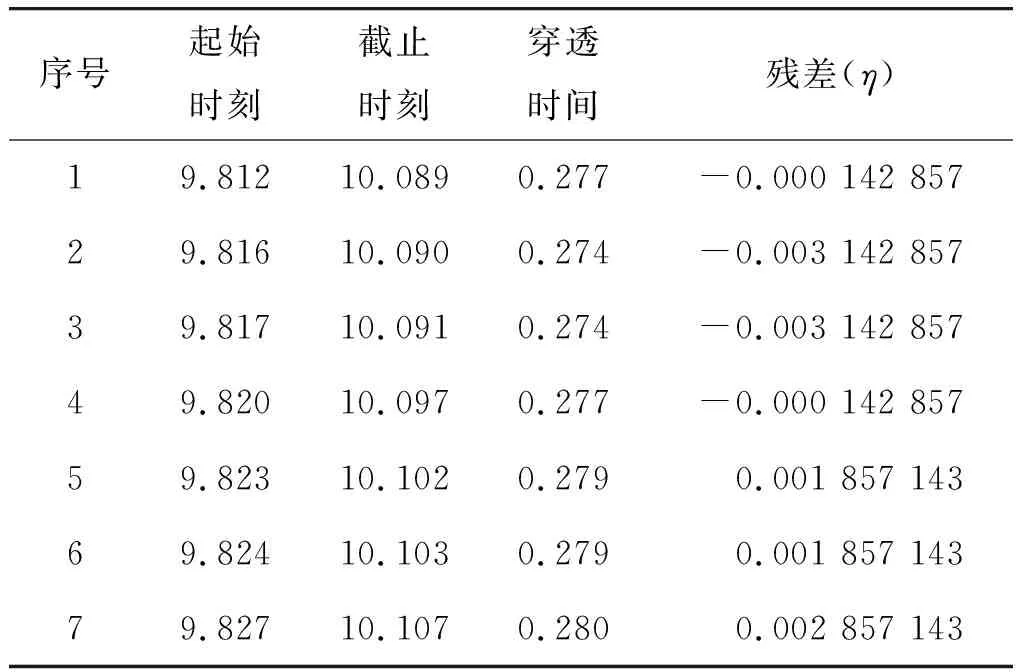
表4 各时间刻点的提取量Table 4 Parameters extracted at different time ms
破片穿透时间t的标准差估计值为:
因此可以认为,测时的随机误差σt<0.003 ms。
6.2 测距随机误差
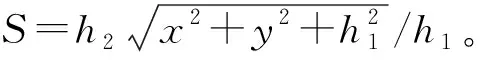
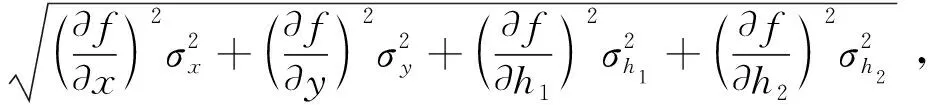
式中:σx和σy为由坐标的读取带来的随机误差;σh1和σh2为由定向屏和光幕的间距测量带来的随机误差。
坐标读取误差和定向屏、光幕误差可以通过多次读取来计算。
6.3 实际验证
以某次试验中的某光幕靶为例,接收到的5个破片其飞行的距离相对差和测速相对误差如表5所示。
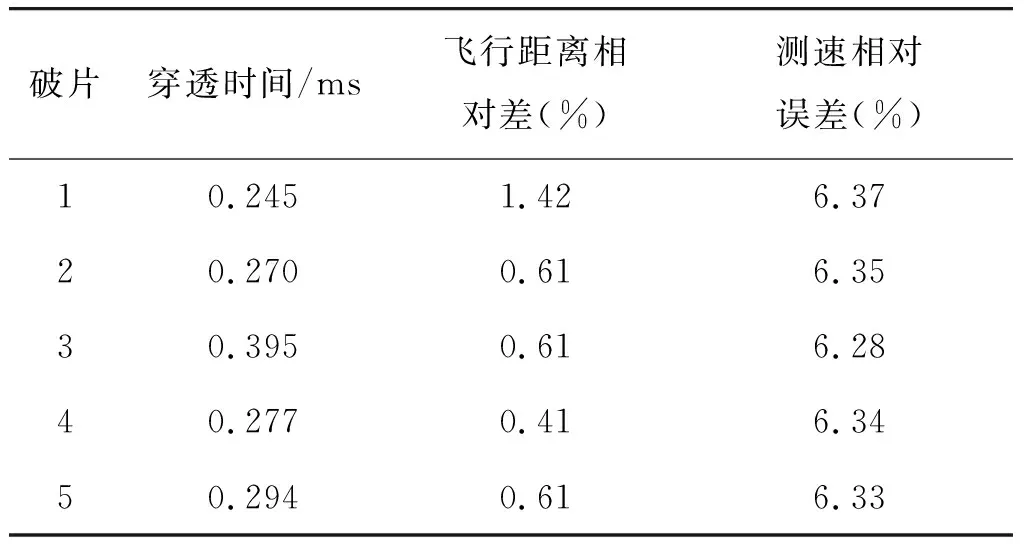
表5 误差的计算结果Table 5 Computaion result of velocity error
7 结束语
本文主要通过分析设备工作原理、破片飞行规律等因素,提出了对时间信息、位置信息进行准确匹配的方法。通过对光幕靶破片速度测量误差的分析和计算,较为精确的建立破片速度误差计算模型,对于控制破片速度测量的精度以及分析评估破片毁伤效果提供了精确可靠有效的支持,对于提高和改进破片速度测量方法有积极意义。

