引入系统不确定度的模糊IAE-UKF组合导航
邢东峰,张琳婧*,杨菊花,陈光武,刘 昊
(1.兰州交通大学自动控制研究所,甘肃兰州730070;2.兰州交通大学甘肃省高原交通信息工程及控制重点实验室,甘肃兰州730070;3.兰州交通大学交通运输学院,甘肃兰州730070)
1 引 言
在交通应用中有两种较广泛使用的位置服务方法,分别为全球定位系统(Global Positioning System,GPS)和惯性导航系统(Inertial Naviga⁃tion System,INS),GPS/INS组合系统具有互补性,从而比任何一个独立系统都能够提供更加准确和强大的导航方案[1]。随之而来的问题即为如何选择组合结构与组合方法,针对低成本组合系统,松耦合的组合结构一般满足需求,即可将问题整合转化为非线性滤波[2]。由于任何系统都存在不同程度的非线性,用线性滤波处理则代表默认忽视了实际情况中的非线性,尤其是对低精度传感器构成的组合导航系统。将线性处理非线性系统导致的一系列问题归结为系统模型建立不准确的问题,运载体的类型、所处环境、机动性大小、精度需求的高低等对其都有影响,需要分别对待具体问题,所以目前并没有一个统一的处理方式,但总是有迹可循的。组合导航主要解决的是随时间逼近和跟踪的目标点连续定位问题[3],在传感器数据融合层的过程中,每一次的递推过程都被系统的不确定性影响。无论是何种滤波算法,它们正常运行的假设为系统模型是准确的。
扩展卡尔曼滤波(Extended Kalman Filter,EKF)将非线性进行近似线性处理[4],雅可比矩阵推导过程较繁琐。无迹卡尔曼滤波(Unscent⁃ed Kalman Filter,UKF)不需要推导雅可比矩阵且精度较高[5],UKF求解预测值和量测值时需要应用系统模型的采样点信息,但系统模型采样点初始信息的不确定性容易导致滤波器发散,从而增大状态估计误差,所以如何量化并限制系统的不确定性是重点。使用较广泛的克服系统不确定性的方法有强跟踪、渐消遗忘因子、模糊控制、集成控制等[6-9]方法。在不确定性因素的影响下,一致的状态估计是滤波估计器有效工作的重要保证,并且要考虑是否存在过度收敛。交互多模型算法的噪声匹配[10]与新息估计[11]都可以使得自适应程度达到最佳,前者的计算量随着预设模型增多而增大。对此,本文基于滤波器的量测输出中隐含关于系统模型信息的事实[12],引入了新息自适应估计(Innovation Adaptive Estimation,IAE)方法[13]控制滤波稳定。
针对低成本组合导航系统,在载体机动性变化时,系统该时刻的不确定性不同于系统最初建模时的不确定性,当改变后的不确定性作用于系统,会导致滤波精度下降,同时滤波器工作稳定性降低。不同于将组合导航建模处理为预设、评估或者假设、检验的问题,本文将建模问题设定为判断、明确、控制的问题,不需要精确的数学模型且便于实时处理。
2 系统不确定度
由组合导航滤波模型[14],系统的观测值为为一步预测,得到预测残差如式(1):

其中,rk的本质为滤波观测量与状态一步预测之差,包含量测与系统模型信息,通常称其为新息。当系统是一致可观与可控时,滤波被认为处于稳定状态,此时的新息序列为零均值、方差如式(2)的平稳白噪声[12],并且服从δrk∼N(0,σ)的正态分布,将式(2)归一化得式(3):
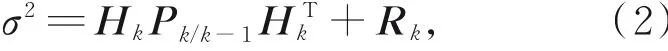
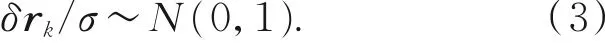
从新息的角度给出滤波器不稳定工作时的解释,归结为两种情况:
(1)由系统模型不准确所引起的状态估计偏差,具体表现在对系统噪声方差阵Q的估计,此时的预测误差方差阵Pk/k−1失去了反应状态估计值的真实性(标准卡尔曼滤波将量测噪声方差的统计特性看作固定值);
(2)由外部观测噪声不准确所引起的观测精度下降(包含量测野值与量测噪声时变两种情况),具体表现为对量测噪声方差阵R的估计,当新息序列突变,此时的滤波增益Kk会使递推值偏离状态估计真实值,导致出现系统发散。
针对情况(1),本文首先明确系统模型的准确度,然后根据新息含义对系统模型进行不确定度的估计,最后依据不确定度设计模糊隶属度函数进行系统噪声方差的在线调整。针对情况(2),本文为使得量测在滤波过程中一直保持稳定且有界,引入IAE方法对量测噪声方差R进行自适应估计,克服量测突变导致的滤波发散。最后探讨同时调整Q与R的成立条件,嵌入UKF算法框架中,实现组合导航。
由新息含义式(1),给定系统不确定性的量化参数γ:

其中,γ为估计量残差与理论残差期望的比值,将γ作为滤波是否发散的判据,γ的理论比值接近1[15],当γ异常大时,则判定滤波发散。新息期望如式(5):
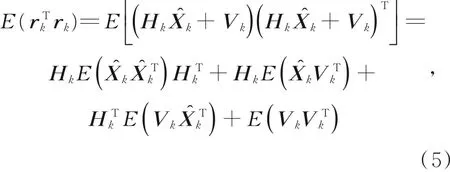

则根据式(4)与式(6)可得参数γ。当γ增大时,系统不确定性增加,当γ减小时,系统不确定性减小。若预先给定参数的上下界,当γ<γmin时,系统不确定程度可接受,认为系统建模准确;当γmin≤γ≤γmax时,系统不确定度较大,系统模型较为准确;当γ>γmax时,量测被认为失去真实性,系统模型不准确。由于γmin与γmax一般根据经验给定,同样的经验值在不同情况下可能有不同效果,在此引入平滑加权残差平方(Smoothed Weighted Residual Squared,SWRS)思想[16],定义系统不确定度Uk,并给出量化式如式(7)所示:

定义系统初始不确定度U1=1,α为自适应因子,取α∈(0,1),取γ0=max[1−α,γ]。Uk在自适应因子α的作用下被膨胀化;残差项rTkrk在量化参数γ0作权值的处理下保证Uk的准确性。即Uk利用新息的统计特性,拥有表示系统模型不准确度的含义,并为噪声的在线估计提供计算基础。区别于只对状态模型进行评估的方法,引入的新息序列包含状态与量测的信息,可以较全面地表示此刻系统模型准确度。当系统工作不稳定时,γ偏离1,系统残差项较大,此时的Uk在权值作用下被修正;当系统工作稳定时,γ接近1,误差项量值较小,Uk保持稳定并趋于平滑。Uk越小代表系统模型越准确,Uk越大,代表系统模型越不准确,从而可以将Uk作为调整模型的依据,作用于增强滤波。
3 IAE算法
调整系统模型的过程实际上为对噪声进行实时估计的过程,由于UKF要求量测噪声先验已知,所以本文基于新息的统计特性,引入滑动窗口的新息自适应估计方法。定义滑动窗口的宽度区间N∈[Nmin,Nmax],滑动窗口的IAE算法步骤描述为:
Step 1:计算状态的一步预测量与状态协方差的一步预测量;
Step 2:根据Nk−1计算修正量测噪声矩阵系数;
Step 3:梯度检测量测噪声矩阵系数在线更新Nk;
Step 4:计算滤波增益Kk,更新状态估计与状态协方差。
滑动窗口IAE算法相比较于传统IAE算法,增加了滑动窗口N的计算选取环节。对计算的准确性描述,N值越大,Cˆrk的估计值越准确,同时自适应灵敏度降低,所以N值的选取需要在准确度与跟踪灵敏度中取得平衡,从而更为准确;对计算复杂度进行量化分析,滑动窗口主要增加了梯度检测函数和N值的实时计算,梯度检测函数中涉及到对角阵矩阵的求逆运算,可以将其转换为除法运算。所以,相较于传统新息自适应算法,滑动窗口IAE算法所增加的计算量并不大,并且滑动窗口的优势可以在滤波灵敏度与准确度中做出较好的取舍[17]。具体表现在序列长度为N的采样区间内,历元新息方差的N值随着每一次离散递推的完成都会发生变化,以下给出滑动窗口IAE的具体推导过程。
根据新息序列自适应滤波,假设条件为系统噪声稳定,量测噪声随时间段变化,且各段噪声互不相关、强度未知,同时滑动采样的有限N个新息具备遍历性,并且式(8)表示的新息方差Crk为关于r的相关函数,此时滤波的量测噪声方差R更新如式(9),针对R的梯度检测函数见文献[17]。
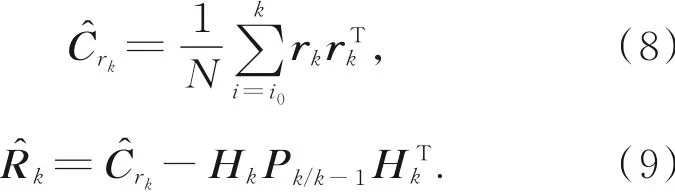
根据中心极限定律,采用高斯概率密度函数表示观测向量Z的条件概率密度函数如式(10),记R对角线上的系数如式(11):
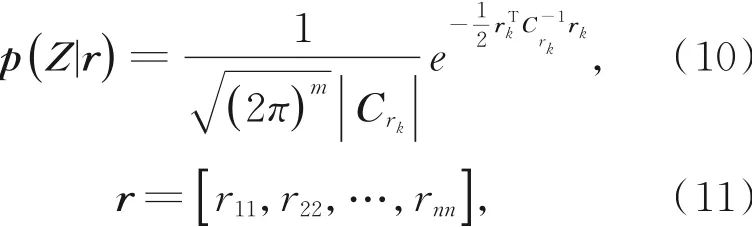
对式(10)取对数得:

式中m为观测量维数,求ln|Crk|对r的偏导:

根据极大似然准则对式(12)取最大值,则:得到:对式(8)求r的偏导:
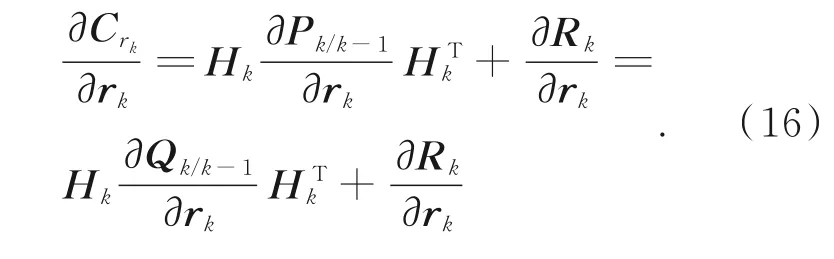

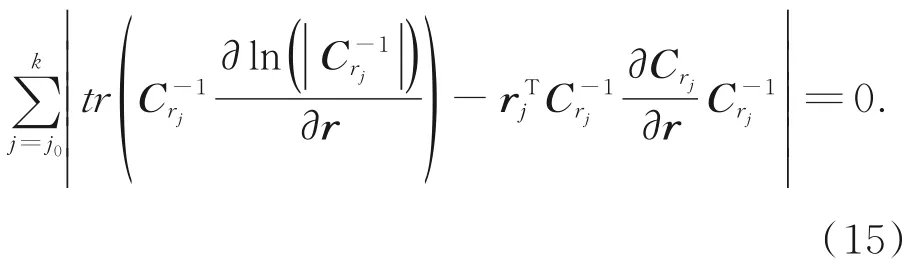
已知R,记r=[q11,q22,…,qmm]为Q对角线上的噪声系数,且R与r独立,将式(16)代入式(15)得:则k时刻的增益矩阵为:

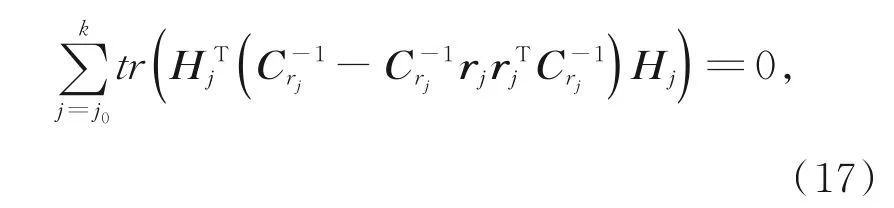
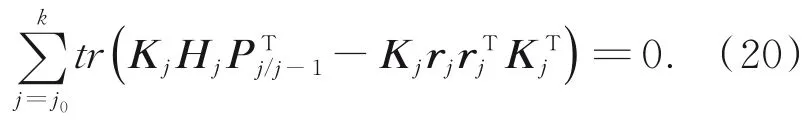
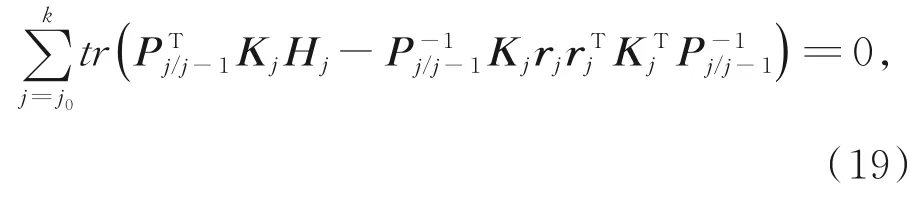
由Pk/k−1−Pk=Kk Hk Pk/k−1,Δxk=Kkrk整理得:

再由Pk/k−1=Φk/k−1Pk/k−1+Qk−1得到系统过程噪声Q的新息序列表达如式(22):
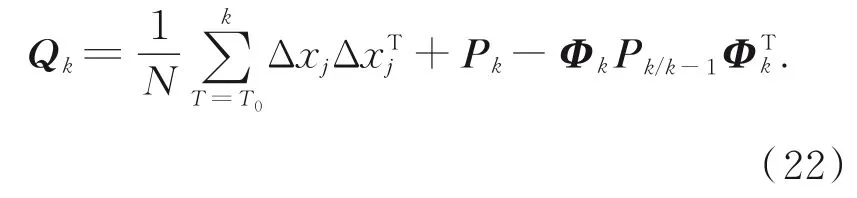
在系统中同时调整系统过程噪声Q和观测噪声矩阵R,与单独调整Q或R阵的条件是相同的,以下给出证明,先将式(16)代入式(15)得:

单独调整R时,假设Rii=rii,Q与r独立时,整理式(23)为:

式(24)成立的条件为式(25):


单独调整Q时,假设Qii=rii,R与r独立时,整理式(23)得:其中,Hj HTj为二次型,必定为非负定矩阵,所以式(26)成立的条件依旧为式(25)。在同时调整Q与R时,假设rii=mRii,rii=nQii,m>0,n>0时,整理式(23)得:
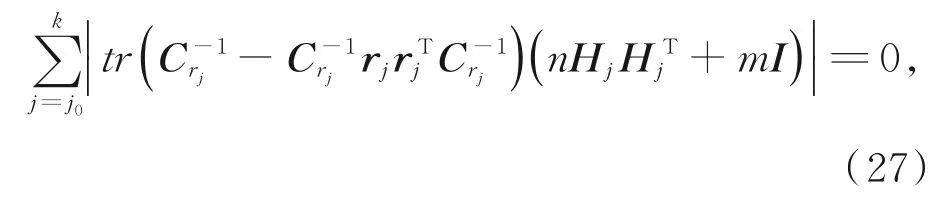
基于以上叙述,结合所定义的系统不确定度U,针对Q阵定义模糊隶属度函数如式(28),γ与σ关系如式(29):


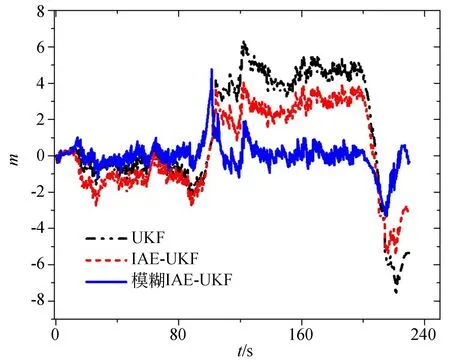
模糊控制器的输入为Uk(k=1,2,3,…,n),输出为σ,σ包含两个模糊集分别为D=减少;I=增加。对式(28)与式(29)描述的模糊规则进行描述,当Uk≤0.1时,表示系统不确定度较小,此时的Q不变;当0.1 量测更新往往是根据频率较低的GPS信息,一旦观测量受到干扰,不仅不能进行误差抑制,而且可能会引入更多的误差。针对量测信号丢失或突变的情况,目前较为广泛的处理方式有两种,分别为检测、构造及适应、调整。前者力求构造一个新的序列去代替原信号,后者使得系统先验知识能够适应系统的时变特性。 本文基于后者的处理思想,设计了一种基于量化系统不确定性的系统模型调整方法。针对低成本组合导航系统,建立组合导航系统为ψ角误差模型[7],如式(30)。取系统状态向量为x=[ψ,δp,δv,εa,εg]T,分别为失准角误差、位置误差、速度误差、三轴加速度计漂移、三轴陀螺仪漂移。 式中:ωen为载体在导航系中相对于地理系的角速度,ωie为地球自转角速度,f为加速计测量得到的比力,fb为加速度计在载体坐标系下的比力,Re为地球半径,加速度计与陀螺仪建模为一阶马尔可夫过程。取系统量测向量如式(31),实现GPS/INS的低成本组合导航系统。 由以上叙述内容,给出模糊IAE-UKF算法流程框图,如图1所示,在UKF滤波框架[19]中嵌入模糊控制与IAE算法,克服系统模型不准确的问题。图1中新息量由蓝色框标注,红色虚线框内为引入不确定度的模糊控制系统,模糊规则由式(28)与式(29)给出,形成了一种并行在线调整GPS/INS组合导航系统模型噪声方差与量测噪声方差的模糊IAE-UKF滤波器(彩图见期刊电子版)。 图1 模糊IAE-UKF算法框图Fig.1 Fuzzy IAE-UKF algorithm diagram 为了验证上述所提方法在车载GPS/INS组合导航系统中的有效性与优越性,设计了车载组合导航的测试,整个系统以INS为主,通过航位推算获得融合信息,试验设备如图2所示。采用GPS卫星板卡与IMU惯性测量单元组合系统,传感器参数如表1所示。 图2 试验设备图Fig.2 experimental equipment 表1 传感器参数Tab.1 Sensor parameters 图3 行驶轨迹Fig.3 Vehicle track 采集了两组数据,第一组数据卫星信号良好;第二组数据卫星信号稳定性较差;且两组数据都存在较大初始姿态误差。第一组数据的行驶轨迹如图3所示。组合导航解的参考值由卫星板卡通过差分(Real-Time Kinematic,RTK)方式获取,其精度在开阔地段精度可达到厘米级,具体参数见表2。从而使用RTK数据进行对比,从误差的角度分析所设计方法的优越性。图4与图5给出了速度误差曲线,显示了非线性滤波算法UKF较线性滤波算法KF的优越性。当存在较大的不可交换误差时,认为载体机动性较高。此时惯性传感器通常有较大的角速度与比力值,状态量的可观性因系统的时变特性也会产生变化,对滤波收敛速度产生一定影响,量测不稳定则影响组合导航解的准确性。 表2 组合位置与速度的误差均值Tab.2 Mean error of combined position and speed 图4 北向速度曲线Fig.4 North speed curve 图5 东向速度曲线Fig.5 Earth speed curve 采用第二组数据进行量测不稳定时的方法验证,行驶轨迹如图6所示。图7~图8给出了不同算法下的组合位置误差,图9~图10给出了组合速度误差。表1列出了组合位置与速度的误差均值,表2列出了组合位置与速度的均方根值(Root Mean Square,RMS)。 图6 行驶轨迹Fig.6 Vehicle track 图7 经度误差Fig.7 Longitude error 图8 纬度误差Fig.8 Latitude error 图9 东向速度误差Fig.9 Eastward speed error 图10 北向速度误差Fig.10 Northbound speed error 表3 组合位置与速度的RMSTab.3 RMS of combined position and speed 由图7~图8,模糊IAE-UKF算法精度较高,位置误差得以明显抑制。由图9~图10,组合速度误差在整个滤波过程中较为平缓,表明模糊IAE-UKF算法受载体机动性影响较小,精度优于传统UKF与IAE-UKF算法。由表1~表3的统计数据分析得,IAE_UKF与模糊IAEUKF算法使得位置误差与速度误差下降在20%以上,其中模糊IAE-UKF算法能够使得误差下降超过60%,验证了文章改进方法的有效性与优越性。 为了更进一步说明设计方法在量测异常情况下的优越性,在第二组数据中设置两个阶段的GPS信号丢失,第一阶段为100~107 s,第二阶段为200~205 s。图11给出了GPS信号丢失情况下的经度误差,图12给出了GPS信号丢失情况下的东向速度误差。表明模糊IAE-UKF方法在GPS信号丢失时能够较块收敛,且能适应由外部量测异常导致不确定性增大时的系统。图13给出了量测正常与量测异常下的不确定度对比。由图13可知,量测正常时,U大范围处于(0,1)内;量测出现异常时,U值越大,代表此刻系统模型的不准确性越大,从而能够根据U值对系统噪声进行在线调整。 图11 经度误差Fig.11 Longitude error 图12 东向速度误差Fig.12 Eastward speed error 图13 系统不确定度UFig.13 Uncertainty of the system U 文章以提高低成本GPS/INS组合导航系统的滤波精度为目标,在初值姿态误差较大时,使用非线性滤波算法克服组合导航系统的不确定性。首先给出了系统不确定性的含义,其次利用新息含义式给定量化参数γ与U的权值函数,对不确定度进行量化,引入滑动窗口IAE方法,利用梯度检测函数确定滑动窗口长度N;最后设计输入为U输出为σ的模糊控制系统,生成可自适应调整噪声方差阵Q与R的方法,嵌入到UKF滤波器中,构建了模糊IAE-UKF滤波器。 模糊IAE-UKF滤波器同时考虑Q与R对模型的影响,是一种带有过程噪声方差估计器与量测噪声方差估计器的滤波器,实现在线调整系统模型,抑制系统不确定性对组合导航解的影响。最后通过三组半物理仿真试验验证了提出方法的有效性,为系统的应用提供一定的参考价值。4 模糊IAE-UKF滤波器



5 试验与分析


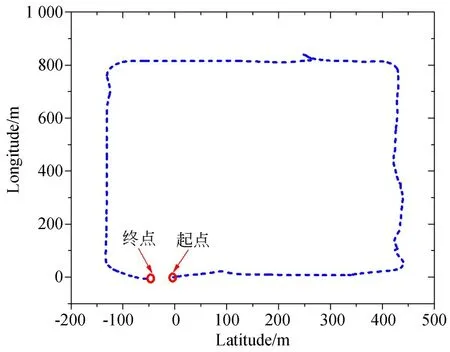
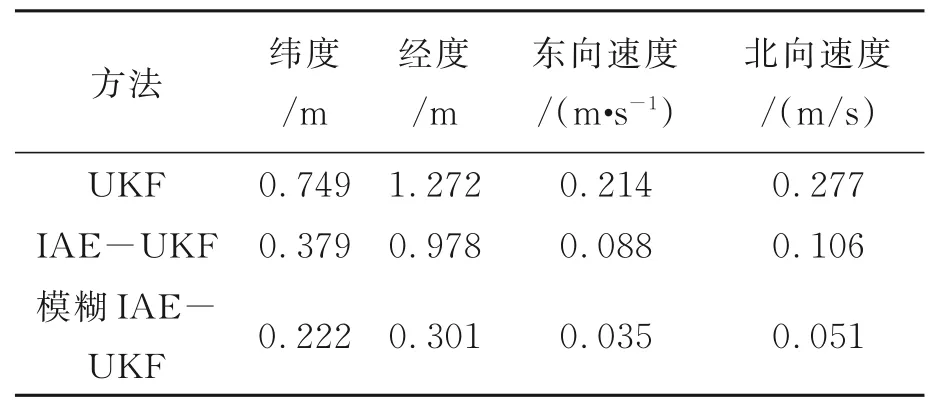

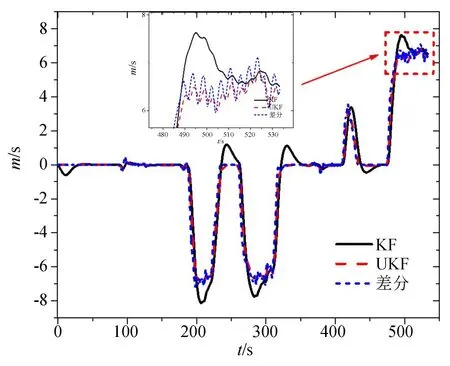
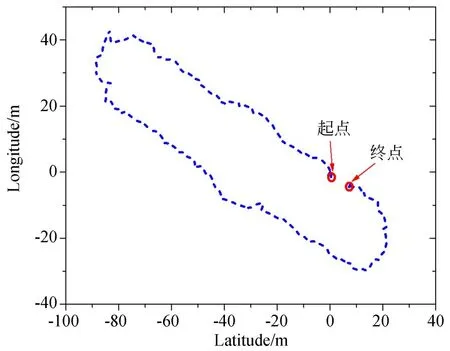

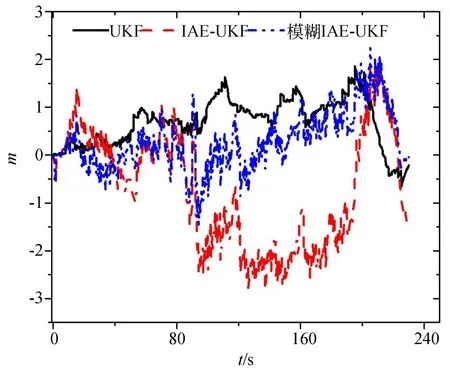
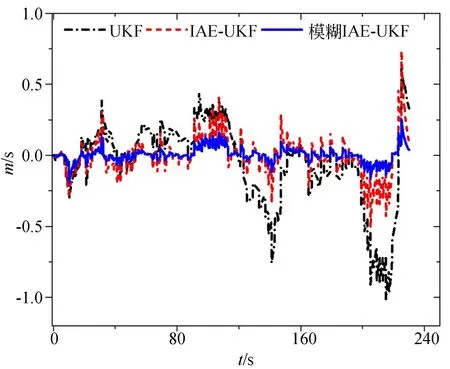
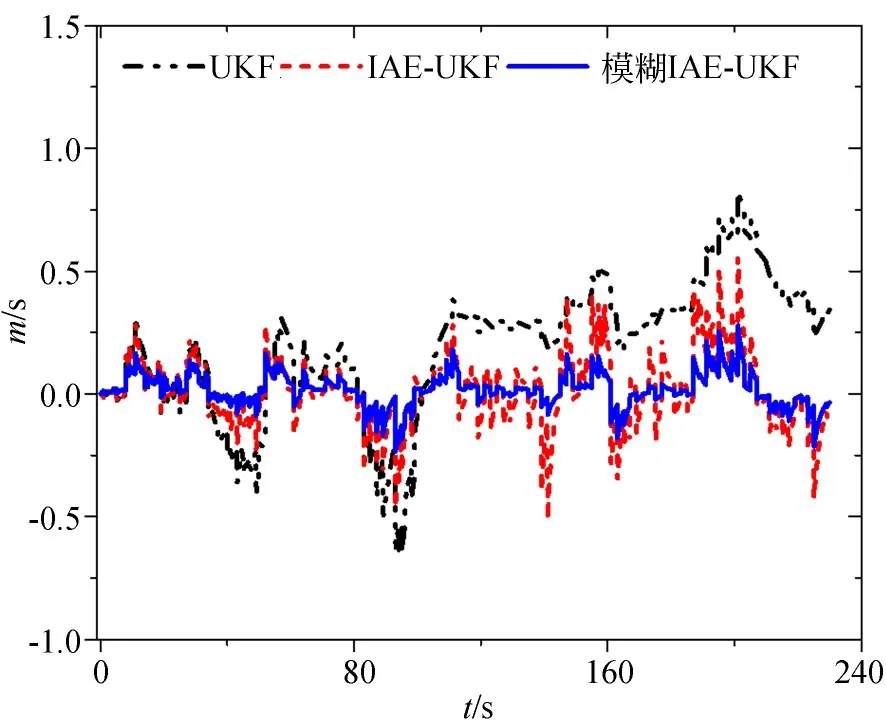
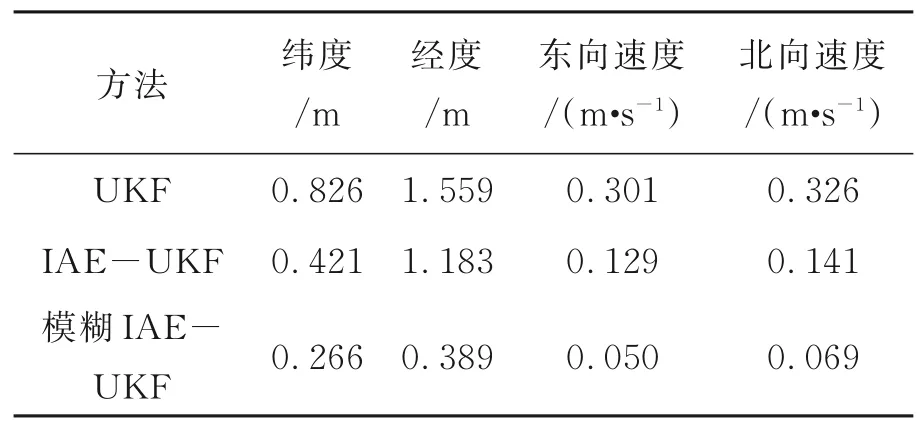


5 结 论

