混合云存储中网络稀疏大数据渗透迁移算法

王娜娜

(山西警察学院 网络安全保卫系，山西 太原 030401)

0 引 言

在物联网、云计算技术飞速发展的背景下，网络中的稀疏大数据数量呈线性增长，社会进入大数据时代[1]。云存储环境是由网络虚拟形成的存储平台，是海量存储设备通过集群技术构成的。数据迁移的本质是将存储设备中存在的数据迁移到其它存储设备中，提高资源的利用率和存储系统的性能。数据迁移分为两种类型，分别是在线迁移和离线迁移。存储系统的性能受数据迁移效率的影响，所以数据迁移在数据管理中是极其重要的。在混合云存储中快速、准确地获取稀疏大数据，对稀疏大数据进行分析，是目前研究的热点[2,3]，相关研究人员提出了一些方法。

文献[4]提出传统RDBMS向非关系型MongoDB数据模型转换与数据迁移方法，构建了代表关系参照完整性的有向图表示模型对数据进行预处理，根据预处理结果提出基于关系型数据模型，运用该模型将数据进行自动转换，从而实现数据迁移。分析实验结果可知，该方法能够按照一定的结构将数据迁移到相应的空间中，但是该方法没有考虑到对特殊样本数据进行检查，导致数据迁移完整度不高。文献[5]通过数据选择阶段和迁移学习阶段完成网络稀疏大数据的迁移。根据级联结构在数据选择阶段中删除网络稀疏大数据中存在的冗余样本和噪声样本，在迁移学习阶段中将权重恢复因子引入Tr Ada Boost算法中，实现网络稀疏大数据的迁移。实验结果表明，该方法具有较高的数据迁移完整度，但是方法实施步骤过于复杂，导致迁移用时过长。文献[6]根据网络稀疏大数据块的级别构建价值评价模型，在价值评价模型的基础上对历史价值系数、数据大小、数据块间关联和读写频词进行量化处理，得到网络稀疏数据块的价值，结合被动迁移阈值和主动迁移阈值实现网络稀疏大数据的迁移。实验结果表明，该方法能够实现对大数据的有效迁移，但是效果不佳，数据不够全面。文献[7]提出基于动态调整阈值的虚拟机迁移算法，对混合云存储中的历史负载数据进行分析，计算网络稀疏大数据在动态调整过程中的阈值门限，通过阈值门限确定预测物理机对应的负载趋势和延时触发，计算数据迁移的时机，完成网络稀疏大数据的迁移。但是该算法完成任务所用的时间与数据迁移前相差较小，存在有效性差的问题。

为解决上述方法中存在的问题，提出混合云存储中网络稀疏大数据渗透迁移算法。针对传统方法没有考虑到特殊冗余样本数据的干扰问题，提出了基于纹理基元直方图的冗余数据筛查方法，采用该方法对冗余样本数据集进行筛查，根据筛查结果将其进行剔除，从而提升网络稀疏大数据渗透迁移效果。实验结果表明，该算法能够有效提高网络稀疏大数据渗透迁移的完整度，并且在数据筛查的基础上提升了数据迁移的效率，使该算法的总体性能得到了提升。

1 网络稀疏大数据渗透迁移算法

数据管理在当今大数据时代中的地位越来越重要。数据管理通常情况下是采用存储系统规整并分析数据，将网络中的稀疏数据转变为信息的过程。提取数据中的关键信息辅助人们工作是数据管理的主要目的。网络数据通常储存在存储设备中，需要对网络稀疏大数据进行迁移。

1.1 基于纹理基元直方图的冗余数据筛查方法

网络稀疏大数据中包含具有极大相似性数据(即存在冗余数据)，因此判断海量网络稀疏大数据中是否存在相似程度较高的数据是最终进行数据迁移的关键。采用基于纹理基元直方图原理[8]，对相似性数据进行筛查，从而实现冗余数据的剔除。

在数据筛查过程中，采集离散有限的时序数据，可表示为

(1)

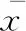
一般地，冗余数据均值是动态变化的，因此需要设定固定时间对数据进行采集，以此来防止数据间的突变现象。根据纹理基元直方图，得出数据在一定阈值范围内变化的特征，可以表示为

(2)

式中：j表示取值系数，p表示数据总体长度。

设定一个阈值W，当W小于Yi时，则可以认定x(t) 中存在异常冗余数据，应当将其进行剔除。W的计算公式为

(3)

根据式(3)构建冗余大数据重组模型为

(4)

(5)

其中，P是去掉极值后的冗余数据均值，Q是对应的标准差。数据分析的效率由网络稀疏大数据迁移过程中的稳定性和高效性决定。通过纹理基元直方图原理完成对冗余数据的准确筛查，实现了对冗余数据的剔除。

1.2 基于主成分分析的数据降维方法

根据冗余数据筛查结果，将信息熵引入主成分分析算法中，对混合云存储中的网络稀疏大数据进行降维处理[9]。采用主成分分析算法对网络稀疏大数据做降维处理之前，通过信息熵过滤掉网络稀疏大数据中存在的无用信息[10]，具体过程如下：

设Un×m是数据矩阵，其中m表示网络稀疏大数据的总数；n是特征或属性的数量。

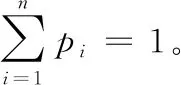
设H是信息熵，其计算公式如下

(6)

设δ是信息熵阈值，对比信息熵阈值δ和属性信息熵H(ai) 之间的大小，如果信息熵阈值δ和属性信息熵H(ai) 符合下式，将属性ai存储到集合中，则有H(ai)>δ。 对集合进行矩阵中心化处理，获得矩阵，其表达式如下

B=A-repmat(mean(A,2),1,m)

(7)

通过计算属性不同的维度之间存在的协方差[12]，得到协方差矩阵Cov，其计算公式如下

(8)

正交分解协方差矩阵Cov，使得协方差矩阵Cov中存在的向量描述向量在特征向量中对应的投影长度，上述投影长度即为向量的特征值[13,14]。计算特征值在投影前为k的分量，消除协方差矩阵Cov中剩余的分量，得到协方差矩阵Cov的特征向量EVR和特征值λi。

k通过特征值对应的贡献率计算得到，贡献率f通过所有特征值和选取的特征值计算得到，贡献率f的计算公式如下

(9)

选取k个较大的特征值构成特征向量Vn×k，得到网络稀疏大数据的降维结果Y

(10)

1.3 基于阈值自学习小波算法的数据去噪处理方法

网络稀疏大数据在混合云存储中通常依赖分布式环境，由于混合云存储中存在大量的噪声[15,16]，所以对网络稀疏大数据进行去噪是亟需解决的任务。根据网络稀疏大数据降维结果，对数据进行去噪处理。混合云存储中网络稀疏大数据渗透迁移算法通过阈值自学习小波算法对降维处理后的网络稀疏大数据进行去噪处理，具体过程如下：

(1)在低通滤波器的基础上通过平滑法对数据进行预滤波处理，去除网络稀疏大数据中存在的白噪声和高频噪声[17]。

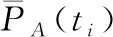
(3)确定分解层数和小波函数对数据进行分解，保持低频信号cj在分解过程中不发生变化，通过软阈值处理各层存在的细节信号dj，通过下式对网络稀疏大数据进行重构，获得首次滤波结果y′1(ti)

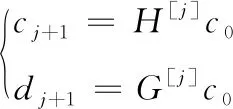
(11)

式中：H[j]是低通滤波器的第j次插零；G[j]是高通滤波器的第j次插零。

(4)设Ek是目标函数对应的均方误差，其计算公式如下

(12)

式中：θ是滤波阈值。设θ(k+1) 是第k+1次滤波对应滤波阈值，其计算公式如下

θ(k+1)=θ(k)+Δθ

(13)

式中：参数Δθ的计算公式如下

(14)

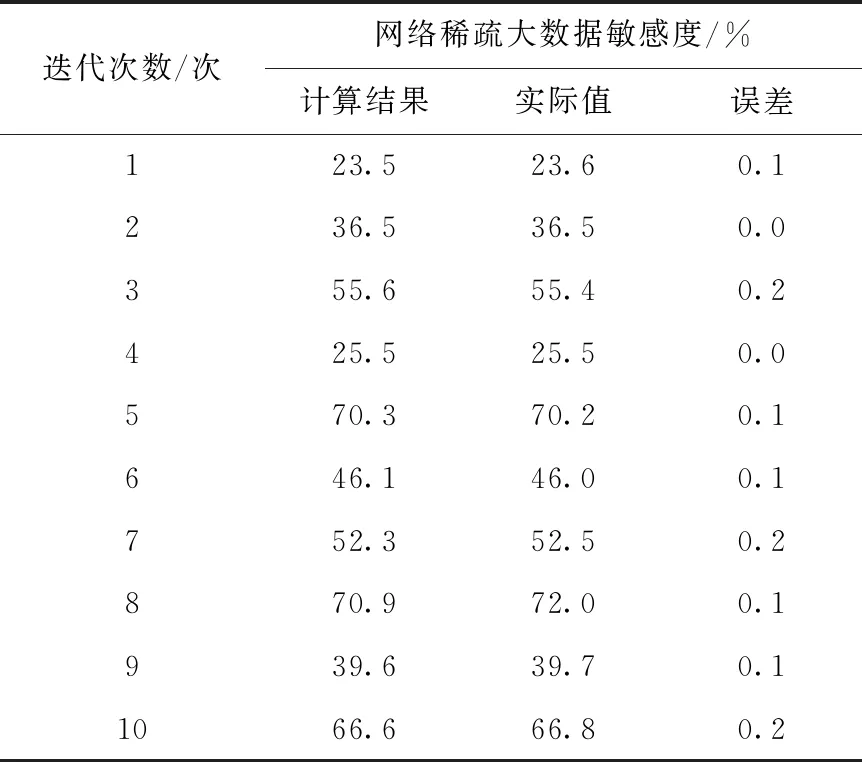
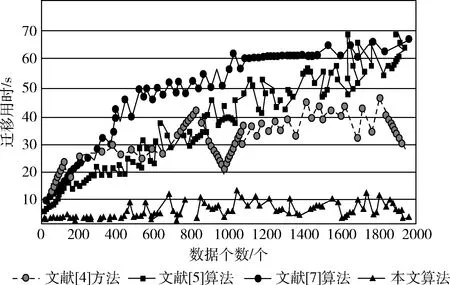
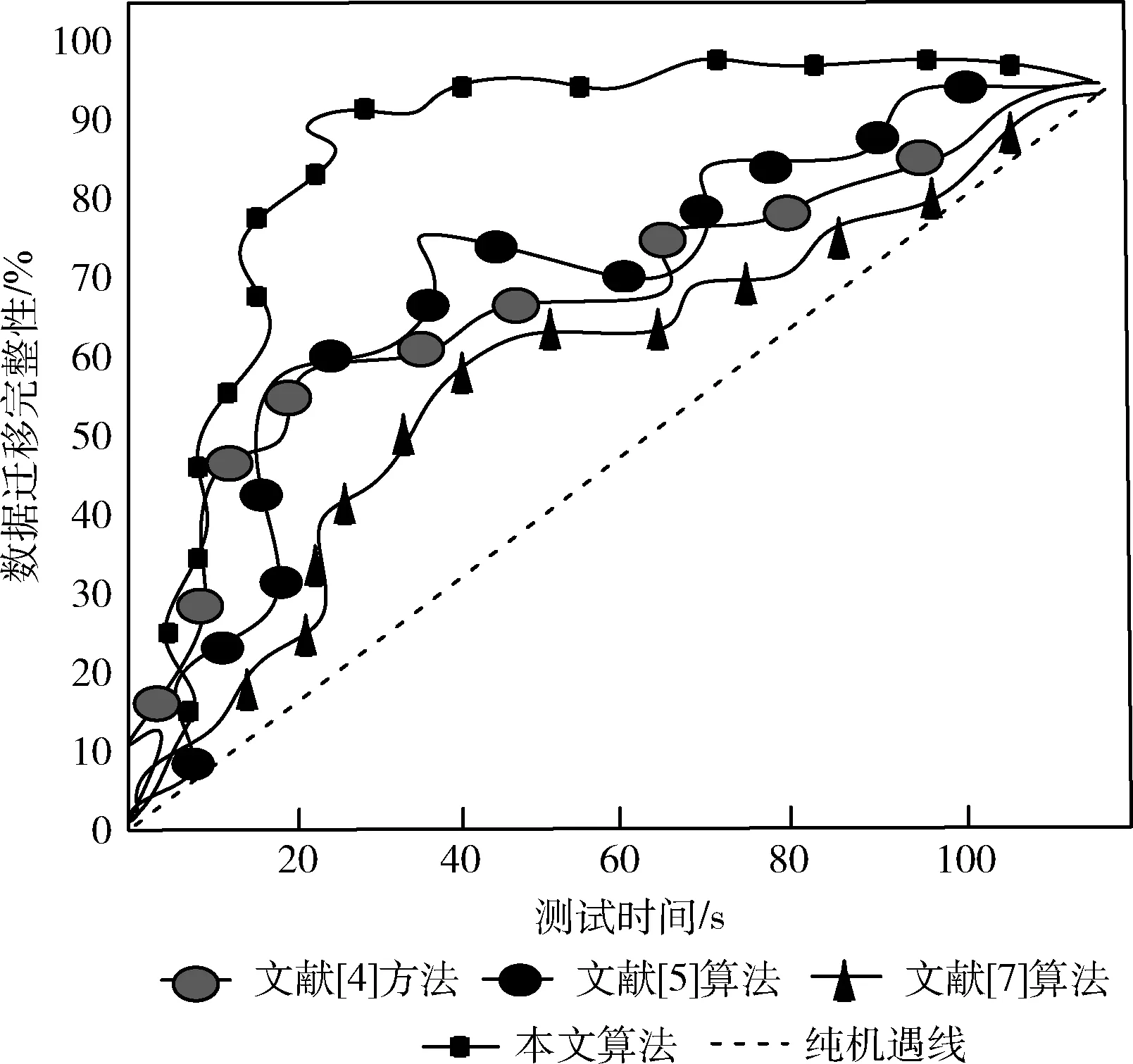
通过滤波阈值对目标Ek进行调整，使其最小。如果Ek

(5)分解测量时间内存在的信号，处理过程与步骤(3)相同，得到去噪后的数据

(15)

1.4 基于迁移函数的网络稀疏大数据渗透迁移的实现

对去噪处理后的网络稀疏大数据进行迁移，设D=[R,S,σ] 是网络稀疏大数据集，其中R是网络稀疏大数据模式；S是网络稀疏大数据集的大小；σ是网络稀疏大数据的敏感度，其计算公式如下

(16)

式中：H是敏感范围阈值；yj、yi是属性集。

在存储系统中数据的访问频率和存储时间会对数据的价值产生影响，在不同阶段中数据的意义都不相同。存储系统中的新数据具有较高被调用的频率，过一段时间后，与新存入系统中的数据相比，这批数据就变为历史数据或是旧数据，被调用的频率变小[20,21]。

设 {t1,t2,…,tn} 是网络稀疏大数据在系统中被访问的时间集；t是当前时间；t-t1,t-t2,…,t-tn是每次访问数据时间和时间t之间存在的长度，将其记为T1,T2,…,Tn。 设T是网络稀疏大数据对应的时间长度，其计算公式如下

(17)

设F是网络稀疏大数据对应的访问频率，fk是数据在Tk时间段内对应的访问频率；fk-fk-1是数据在Tk-Tk-1时间段内对应的存取热度，网络稀疏大数据对应的访问频率的计算公式如下

(18)

数据被创建时，根据网络稀疏大数据特点可知，数据有很大概率被访问，在一定时间内网络稀疏大数据访问频率的增长速度较快，表明网络稀疏大数据在这段时间内的重要性较高[22,23]。网络稀疏大数据被访问后，通常情况下被访问的频率逐渐降低，表明网络稀疏大数据的重要性在该段时间内也降低，将该网络稀疏大数据迁移到其它云存储设备中，提高网络稀疏大数据访问频率。

通过上述分析可知，网络稀疏大数据存储对应的时间长度T与迁移函数之间为正比关系；网络稀疏大数据的访问频率F与迁移函数之间为正比关系；迁移函数与网络稀疏大数据集S之间为反比关系。根据网络稀疏大数据的存储时间长度、访问频率和敏感度[24,25]3个迁移因子构建迁移函数

(19)

通过迁移函数实现混合云存储中网络稀疏大数据的渗透迁移。

2 实验结果与分析

为验证混合云存储中网络稀疏大数据渗透迁移算法的整体有效性，需要对混合云存储中网络稀疏大数据渗透迁移算法进行测试。

2.1 实验参数与环境

本次测试在CloudSim云计算环境中进行，网络带宽为80MI.S-1、内存为8 GB、服务器数量为100台。测试过程中所用的网络稀疏大数据由某信息技术有限公司提供，包括ImageNet、MirFlickr1M、CoPhIR以及MSRA-MM数据集，从上述数据集中抽取2000个数据，并通过SPSS19.0软件处理得到模拟数据，选取的数据集，见表1。

表1 实验数据集的描述

在进行实验之前，首先对数据进行预处理，将数据集划分为10个相等的部分，每一部分都相等，然后从每一部分数据集中随机选取部分数据，用本文算法对网络稀疏大数据的敏感度进行计算，是网络稀疏大数据的敏感度，可通过式(16)计算得到，进行数据迁移之前需要计算网络稀疏大数据的敏感度，根据计算结果判断网络稀疏大数据是否需要迁移。通过上述分析可知，网络稀疏大数据敏感度的计算结果决定数据迁移算法性能。采用混合云存储中网络稀疏大数据渗透迁移算法对某个数据集中的网络稀疏大数据的敏感度进行计算，并将计算结果与实际结果进行对比，见表2。

分析表2中的数据可知，在5次迭代中采用混合云存储中网络稀疏大数据渗透迁移算法计算得到的网络稀疏大数据敏感度与实际敏感度接近，误差均低于0.2，在可接受范围内，不影响网络稀疏大数据在混合云存储环境中的迁移，验证混合云存储中网络稀疏大数据渗透迁移算法的性能较好。

表2 网络稀疏大数据敏感度计算结果

2.2 数据迁移效率对比

根据网络稀疏大数据敏感度计算结果，对混合云存储中网络稀疏大数据渗透迁移算法的性能进行验证。为了验证混合云存储中网络稀疏大数据渗透迁移算法的整体有效性，对比混合云存储中网络稀疏大数据渗透迁移算法、文献[4]方法、文献[5]算法以及文献[7]算法数据迁移中系统执行任务所用的时间，测试结果如图1所示。

图1 不同方法的数据迁移用时对比

分析图1可知，采用混合云存储中网络稀疏大数据渗透迁移算法对2000个数据进行迁移，平均耗时约为5 s，迁移过程未出现拥塞问题，耗时较短；采用文献[7]算法对2000个数据进行迁移，平均耗时约为52 s，在迁移过程中出现了大面积的拥塞现象，导致该算法比本文方法多耗时47 s，说明本文方法在数据迁移过程中更顺畅，耗时更短，效率更高。而采用文献[4]方法和文献[5]算法对2000个大数据进行迁移时，平均耗时约为25 s和48 s；这两种方法在数据迁移过程中都出现了多次不同程度的拥塞现象，导致迁移速度比本文方法速度慢、效率差。对比混合云存储中网络稀疏大数据渗透迁移算法，文献[4]方法和文献[5]算法以及文献[7]算法的测试结果可知，采用混合云存储中网络稀疏大数据渗透迁移算法对网络稀疏大数据进行迁移时耗时更短，效率更高，验证了该方法的有效性。

2.3 数据迁移完整度对比

数据迁移完整度是衡量数据迁移性能的重要指标，因此对本文算法与传统方法进行对比，运用ROC曲线来检验不同方法的数据迁移性能，在ROC曲线图中，存在一条对角线，该线代表辨别力等于0的一条线，也叫纯机遇线，图中曲线距离纯机遇线越远，表明被试方法的性能越强。图2为文献[4]方法、文献[5]算法、文献[7]算法以及本文算法在网络稀疏大数据迁移完整度方面的对比结果。如图2所示。

图2 不同方法的数据迁移完整度对比

分析图2可知，采用混合云存储中网络稀疏大数据渗透迁移算法对网络稀疏大数据进行迁移后，曲线明显距纯机遇线较远，说明该算法的数据迁移完整性较强。采用文献[7]算法对网络稀疏大数据进行迁移后，曲线距纯机遇线最近，说明该算法的数据迁移完整性较差。而采用文献[4]方法和文献[5]算法对网络稀疏大数据进行数据迁移后，曲线离纯机遇线的距离小于本文算法，说明该算法的数据迁移完整性较强，表明文献[4]方法和文献[5]算法的数据迁移完整性效果较差，不能对网络稀疏大数据进行全面性的迁移。对比混合云存储中网络稀疏大数据渗透迁移算法，文献[4]方法和文献[5]算法以及文献[7]算法的测试结果可知，采用混合云存储中网络稀疏大数据渗透迁移算法对网络稀疏大数据进行迁移后，能够得到较为完整的数据集，验证了混合云存储中网络稀疏大数据渗透迁移算法的有效性。

2.4 数据迁移完整度对比

为进一步验证所提算法的有效性，以数据迁移完整度为实验指标对传统方法和本文算法进行对比分析。数据迁移完整度通过式(20)对完整度进行计算

(20)

式中：Xu表示有效数据量，Xv表示冗余数据量，X表示总数据量。运用该公式计算得到文献[4]方法、文献[5]算法、文献[6]方法、文献[7]算法以及本文算法的数据迁移完整度，结果如图3所示。

图3 不同方法的数据迁移完整度对比

分析图3可知，当数据量不同时，数据迁移完整度随之发生变化，总体上来看，文献[4]方法、文献[5]算法、文献[6]方法、文献[7]算法的数据迁移完整度低于本文算法，本文算法的最高数据迁移完整度为90%，明显高于传统方法，这是由于采用本文方法对混合云存储环境中的网络稀疏大数据进行迁移之前，对数据进行去噪处理，降低了混合云存储中的噪声数据，因此达到了提升数据迁移完整度的效果。

3 结束语

网络稀疏大数据在混合云存储环境中具有随机性和自组织特性，需要通过大数据迁移算法实现数据库之间存在的数据调度和数据访问。当前网络稀疏大数据迁移算法的有效性较差，经数据迁移后得出的数据完整性较低，并且不能及时得到迁移结果，提出混合云存储中网络稀疏大数据渗透迁移算法，通过对网络稀疏大数据中的冗余数据进行筛查，去除数据集中的冗余数据，提升了数据迁移的效率，对数据进行降维处理、去噪处理、构建数据迁移模型有效地完成网络稀疏大数据的渗透迁移，为数据库之间的数据调度和访问奠定了基础。根据实验结果可知，本文算法在数据迁移完整度、数据敏感度测试以及数据迁移用时方面明显优于传统方法，说明本文算法具有实际应用优势。但是由于网络中存在着大量的稀疏数据，对其进行迁移必须考虑全面性，因此接下来会在数据迁移研究的过程中，对各种稀疏数据进行研究，以此来提升算法的应用领域。