基于约束聚类的k-匿名隐私保护方法

吴梦婷，孙丽萍，刘援军，胡朝焱，赵延年，罗永龙

(安徽师范大学 计算机与信息学院，安徽 芜湖 241000)

0 引 言

随着互联网技术和移动设备的快速发展，人们可收集、发布和分析的数据规模越来越大，但在对海量数据进行挖掘获得其潜在价值的同时，也给数据的安全和隐私问题带来了极大的威胁。因此，如何在数据发布过程中降低隐私泄露的风险并提高数据可用性已经成为了隐私保护问题面临的极大挑战[1]。

作为一种能有效保证数据真实性和安全性的隐私保护方法，k-匿名[2]技术自提出以来被广泛应用于数据发布和位置服务场景中。Aggarwal等[3]提出将聚类思想运用于k-匿名技术后，有不少文章在基于聚类的匿名隐私保护方面研究出了显著成果。Li等[4]提出了运用反复聚类思想完成模型要求的KACA匿名方法；Yin等[5]提出了一种基于K-member聚类的k-匿名改进模型；Pramanik等[6]提出一种增强聚类的k-匿名算法，并定义了新的数据质量衡量标准；Jiang等[7]提出了一种贪心聚类匿名方法，根据信息损失重新定义距离，并引入贪心思想优化数据集的划分过程；Xing等[8]提出了一种基于k-均值聚类的隐私保护方法；Zheng等[9]提出了一种运用局部最优聚类完成k-匿名的方法，但最终匿名质量受“一次性”聚类影响较大；Fawad等[10]针对稀疏高维数据提出了一种基于k-均值的联合聚类算法，利用高阶随机游走模型计算相似性，并使用多数据点拟合初始聚类中心。但现有的大多数数据匿名化方法严重依赖于预先定义的准标识符概化层关系，缺少考虑离群数据的敏感问题，使得匿名结果产生的信息损失较高并进一步影响数据质量，且无法同时保障信息损失和时间效率趋于最优。针对上述问题，本文提出了一种基于约束聚类的k-匿名隐私保护方法(k-anonymity method based on restrained clustering by threshold，KAM-RCT)。

1 问题模型与定义

1.1 基于聚类的k-匿名

基于聚类的k-匿名问题的核心思想是将k-匿名问题转化为一种带约束条件的聚类问题[11]，问题具体定义如下：

定义1 基于聚类的k-匿名问题。将待发布数据表T(t1,t2,…,tn) 划分成一系列的簇，使得每个簇至少包含k个元组，以满足生成k-匿名等价类，并要求簇内间距总和最小。基于聚类的k-匿名问题的最优解是划分完成后的等价类集合E={e1,e2,…,em} 满足以下条件：

(1)∀i≠j∈{1,2,…,m},ei∩ej=∅;

(2)∪i=1,2,…,mei=T;

(3)∀ei∈E,|ei|≥k;

1.2 距离度量函数

在聚类算法中，定义距离函数用来度量数据之间的相似度是衡量聚类结果的关键因素。由于准标识符属性中包含数值型数据、二元型数据和分类型数据3种不同的数据类型，故本文以最小信息损失为目标，针对不同类型的数据分别定义其距离度量函数。

定义2 数值型数据间的距离。设D为连续型有限数值域，任意两个属性值vi,vj∈D，vi,vj间的距离定义为

(1)

式中： |D| 表示连续型有限数值域D中最大值和最小值之间的差。

定义3 二元型数据间的距离。二元型是指数据只用两种值表示，分别是0和1，对于任意两个二元型数据vi,vj之间的距离定义如下

(2)

对于分类型数据，由于通常其属性的取值是有限或离散的，且属性值之间不具备完整的序关系，所以数值型数据和二元型数据间的距离定义并不适用于分类型数据。但是，大多数分类型数据值之间存在某种语义相关性，这种语义相关性通常可以由分类树来体现。

定义4 分类型数据间的距离。设D为分类型属性域，TD为属性的分类树，任意两个分类型属性值vi,vj∈D，vi,vj间的距离定义为

(3)

式中：H(TD) 表示分类树的树高，H(Λ(vi,vj)) 表示vi,vj在分类树中最小公共子树的高度。

基于数值型、二元性和分类型数据的距离定义，两个元组间的距离定义如下：

定义5 元组间的距离。表数据T的准标识符为QI={N1,…,Nm,B1,…,Bn,C1,…,Ck}，Nx(x=1,…,m) 表示数值型属性，By(y=1,…,n) 表示二元型属性，Cz(z=1,…,k) 表示分类型属性，则任意两个元组ti,tj∈T之间的距离定义为

(4)

式中：ti[A] 表示元组ti在属性A上的值。

1.3 信息损失函数

由于k-匿名聚类问题最终是要将划分好的簇在准标识符上进行概化，得到若干个等价类。保护隐私的同时，属性在概化过程中必然导致表数据的信息损失，最终概化得到的值越模糊，信息损失就越多。因此，为了更加合理地衡量信息损失度，本文考虑不同属性类型的特点，分别计算数值型和分类型属性匿名后的信息损失。

对于元组中的数值型属性，a为某属性原始值，[amin,amax] 表示其概化后的区间，其中amin表示该属性在元组所在等价类中的最小值，amax表示该属性在元组所在等价类中的最大值，设D为属性的有限数值域，则元组中该数值型属性的信息损失为

(5)

对于元组中的分类型属性，依据构建的属性分类树，Size表示以最大程度概化后的值为根结点的总叶子数，size(g)表示概化结果子树的叶子个数，则元组中该分类型属性的信息损失定义为

(6)

定义6 等价类的信息损失。等价类的信息损失是指对簇e内所有元组的每个准标识符进行匿名处理后造成的信息损失CIL，即为所有属性的信息损失之和，d表示准标识符属性的个数，则等价类的信息损失定义为

(7)

基于以上定义，可定义匿名数据表的总体信息损失如下：

定义7 总体信息损失。将匿名数据表T*划分成的等价类集合表示为E={e1,e2,…,em}，则所有等价类的信息损失之和为总体信息损失，具体定义为

(8)

2 基于约束聚类的k-匿名隐私保护方法

2.1 KAM-RCT算法

针对现有的基于聚类的k-匿名隐私保护算法存在信息损失高、对离群数据敏感等问题，本文提出了一种基于约束聚类的k-匿名改进算法KAM-RCT。算法利用KNN算法思想进行集群初始划分，通过引入阈值约束迭代过程，从而提升了聚类算法的性能。

如图1所示，算法由4个基本部分组成：第1部分在待发布的数据表T中随机选取m个初始聚类中心；第2部分利用KNN思想进行全局聚类，将距离聚类中心最近的k-1 个元组添加到相应的簇中，划分结束后更新聚类中心；第3部分根据信息损失阈值δ对等价类进行重新划分，计算每个等价类的信息损失，若大于阈值δ则将该等价类中元组放入待分配集合R，即去除聚类表现不佳的簇，然后在保证等价类的信息损失满足阈值δ的前提下将集合R中的元组划分到相应的簇中，每次簇内元组发生变化后及时更新聚类中心；第4部分对每个等价类按照预先定义的规则进行匿名化处理。算法充分考虑离群点对聚类结果的影响，划分过程始终都以信息损失最小化原则选取元组，有效减少匿名过程中的信息损失。KAM-RCT算法具体实现步骤如下：

算法： 基于约束聚类的k-匿名隐私保护算法

输入： 待发布的数据表T，匿名参数k，阈值δ

输出： 满足约束条件的匿名数据表T*

(2) InitializeE←{ei|ei←{ci},ciis randomly picked fromT,i∈[1,m]}

(3)fori←1 tom

(5)endfor

(7)foreachei∈E

(8) CalculateCIL(ei) by Equation(7)

(9)if(CIL(ei)>δ)

(10)R←R∪ei

(11)E←E-{ei}

(12)else

(13) Update the center ofei

(14)endif

(15)endfor

(16)whileLen(R)>kdo

(17)foreachrj∈R

(18)foreachei∈E

(19)ei←ei∪{rj}

(20)if(CIL(ei)<δ)

(21)R←R-{rj}

(22)else

(23)ei←ei-{rj}

(24)endif

(25)endfor

(26)endfor

(27) Update {c1,c2,…,cm}

(28)endwhile

(29)foreachei∈Edo

(30)T*←T*∪Anonymization(ei)

(31)endfor

图1 KAM-RCT算法基本框架

2.2 KAM-RCT算法分析

2.2.1 正确性分析

本文是实现将包含n个元组的数据表T划分为多个等价类，使得每个等价类中的元组数大于匿名参数k，且保证匿名后的总体信息损失TIL达到最小值。由2.1节给出的算法可知，第(2)行-第(6)行每个簇在初始化过程中会选取距离聚类中心最近的k-1个元组，保证初始生成的每个簇大小都为k，已符合k-匿名模型的元组要求。第(7)行-第(28)行根据阈值δ删除信息损失高的簇，并将这些簇内的元组划分到相异度最低的簇，然后更新每个簇的聚类中心。聚类划分过程的每一步都以信息损失度最小为目标，得到的每个簇的大小至少为k，始终满足k-匿名模型的基本要求。第(29)行-第(31)行，对每个簇进行概化匿名处理，使得相同等价类中的元组在准标识符属性上无法区分，最终得到满足要求的匿名数据表T*。

2.2.2 复杂性分析

设n为原始数据表T中的元组个数，d为准标识符属性个数，算法第(5)行完成后得到m个簇，有11)。

算法在第(3)行-第(5)行中，每生成一个新的簇ei需k-1遍扫描T，并计算T中每个元组与聚类中心ci在准标识符上的相应距离，一共生成m个簇，因此，执行时间为O(dkmn)。

算法在第(7)行-第(15)行中，对m个簇依次计算其在准标识符上的总信息损失CIL(ei)，因每个簇中至少有k个元组，故执行时间为O(dkm)。

算法在第(16)行-第(28)行对集合R中的元组进行重新分配，集合中元组个数为 |R|，需计算每个元组依次放入每个簇后簇的信息损失，因此，执行时间为O(|R|dkm)。

算法在第(29)行-第(31)行中，对每个簇进行匿名处理并生成匿名数据表T*，该过程需在依次遍历所有元组的同时概化其准标识符属性值，因此，执行时间为O(dn)。

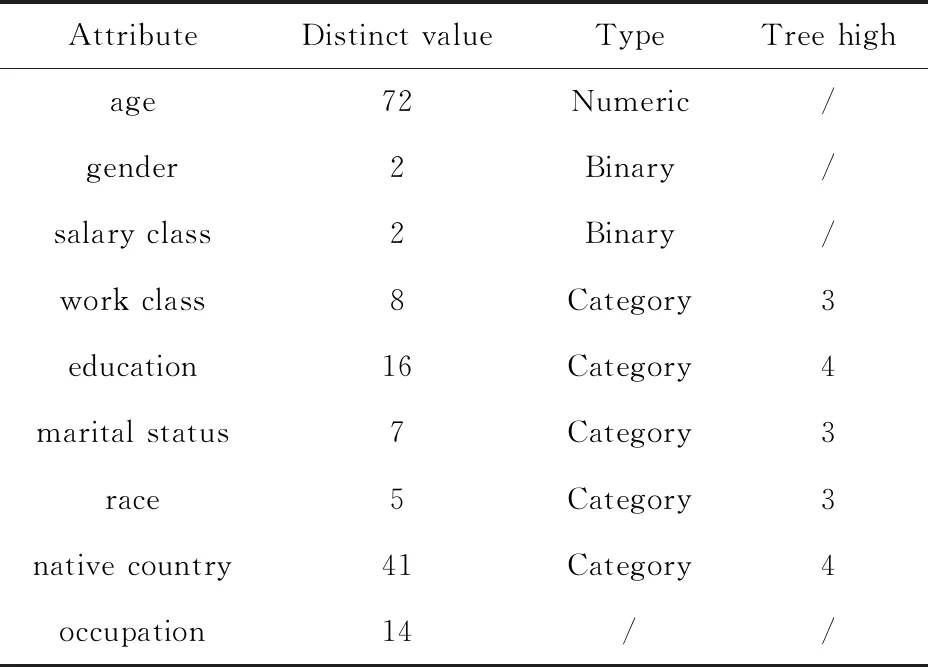
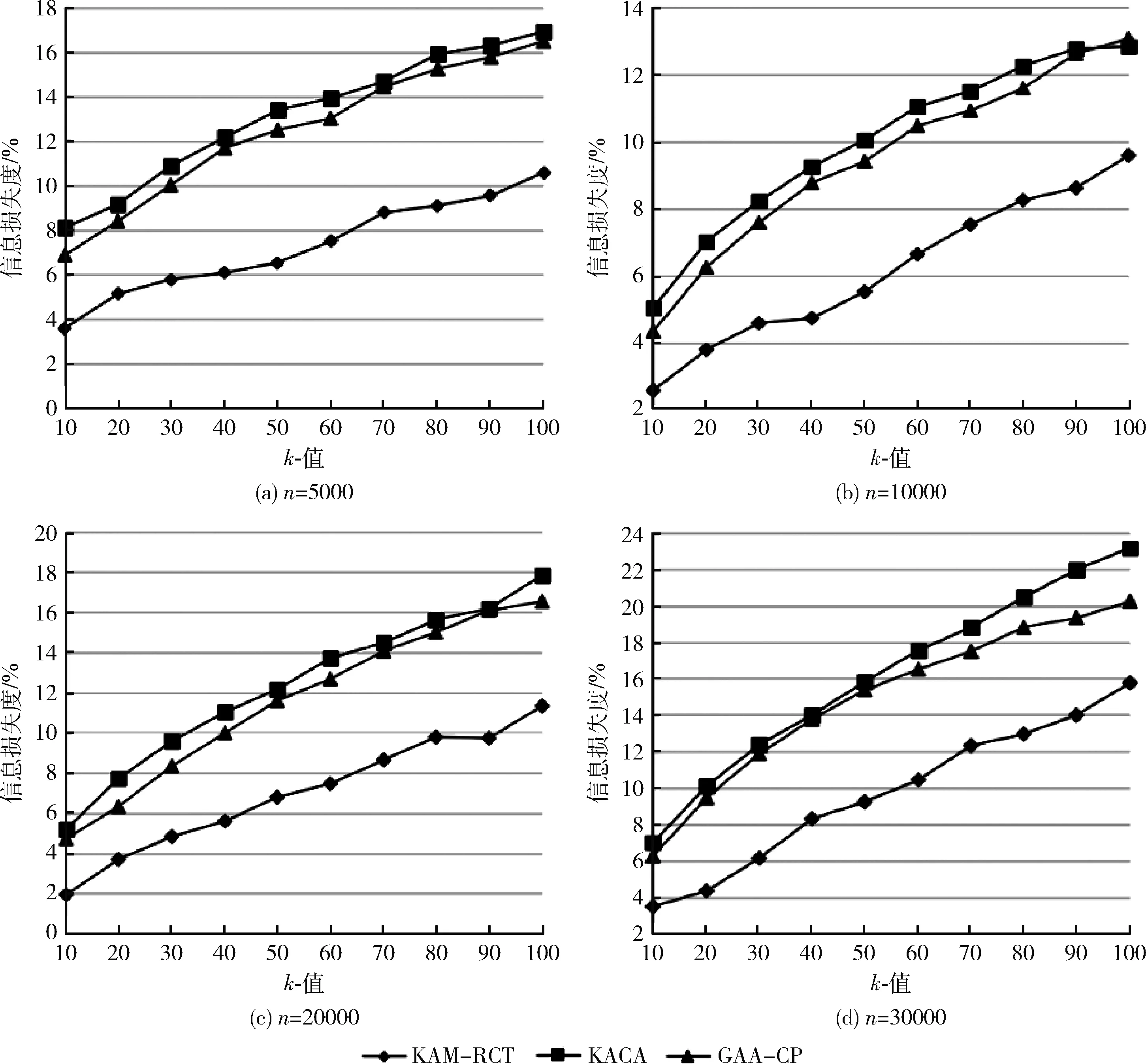
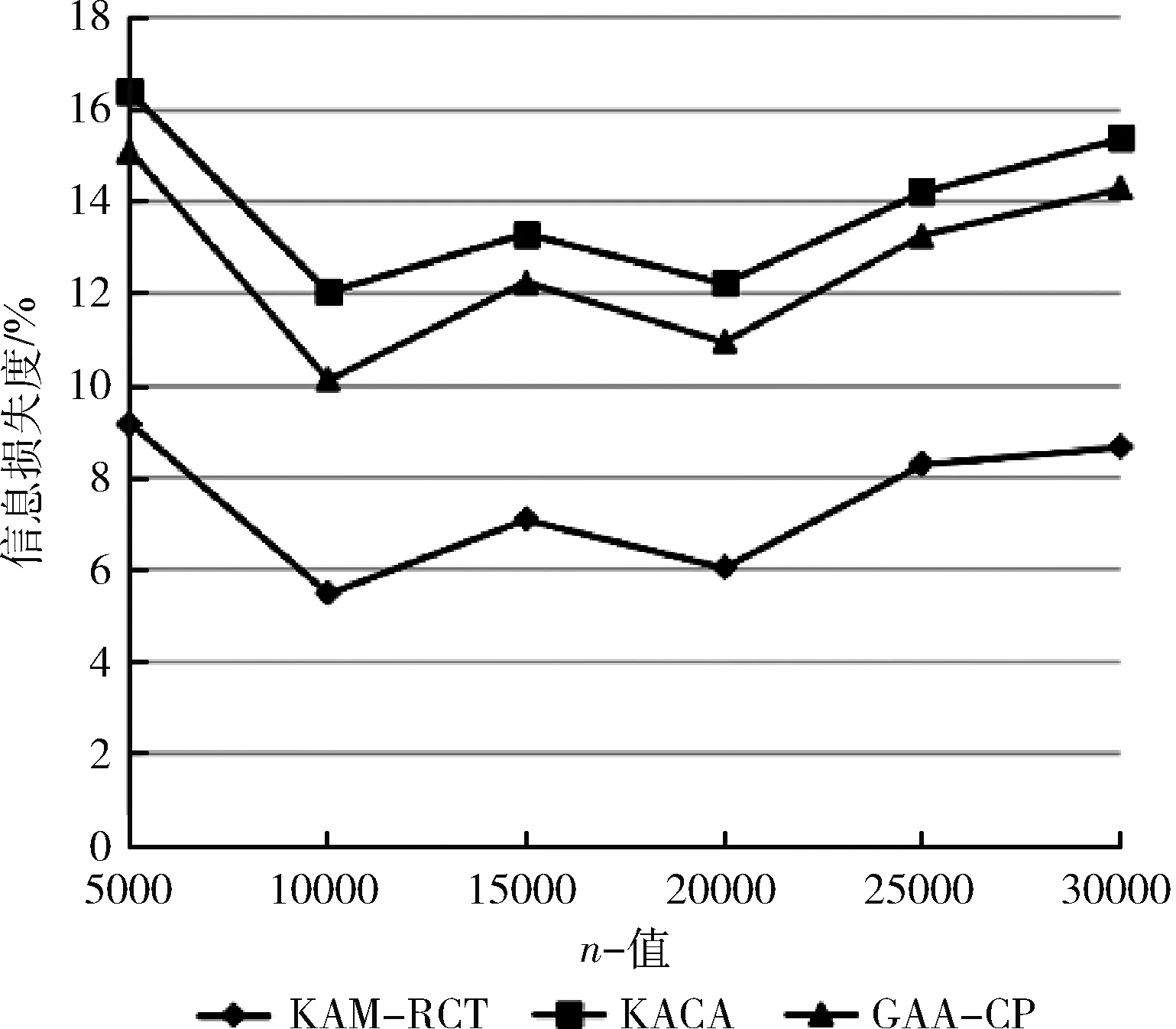
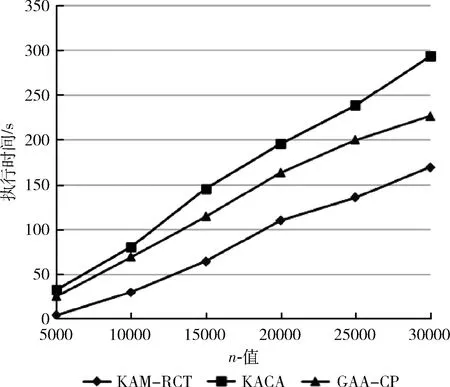
因此，KAM-RCT算法总的时间复杂度为O(dkmn)+O(dkm)+O(|R|dkm)+O(dn)=O(dkmn)。 由于km

3 实验与结果分析

本节通过对典型数据集进行实验，验证KAM-RCT算法的性能，并将其与文献[4]中基于多维全域泛化的KACA算法和文献[7]中贪心聚类匿名GAA-CP算法进行比较，对比分析结果表明本文所提出的基于约束聚类的k-匿名隐私保护方法在匿名数据的信息损失度方面相较于其它算法有明显的优势。

3.1 实验环境及数据集

本文实验的实验环境为：Intel Core i7-7700HQ @ 2.8 GHz，24 GB内存，算法由MATLAB 2018b实现，程序运行在Windows 10环境下。

本文实验采用的Adult数据集来源于UCI机器学习库(http://archive.ics.uci.edu/ml/)，由部分美国人口普查数据构成，目前被广泛使用于数据匿名化隐私保护领域[12]。实验开始前先对数据进行预处理[13]，删除了含有缺失属性的数据后，从中随机选取5000-30 000个元组作为此次的实验数据集T。对于每一个元组都提取了9个属性值，依次为age，gender，salary class，work class，education，marital status，race，native country和occupation，其中 occupation 为敏感属性，其余8个为准标识符属性，实验数据信息见表1。最后，算法完成等价类划分后，对每个等价类进行匿名处理[14]。考虑到各个算法最初随机选取聚类中心会对最终结果有略微影响，本文中每组实验重复进行20次，结果取其平均值。

表1 Adult数据集信息描述

在保证数据质量和运行时间的前提下，本文使用的信息损失阈值δ由多次实验取得，实验在不同数据量的Adult数据集上进行，通过限制待分配集合R中的元组个数寻找最佳的阈值δ，从而得到最优的总信息损失，实验结果发现阈值δ和匿名参数k之间存在线性关系。因此，将δ和k进行线性拟合后，再用线性函数求出δ并带入分析实验。

3.2 信息损失分析

为分析数据信息损失度随着匿名参数k的改变而变化的规律，我们通过一组实验对3种算法进行比较，图2中的4张图分别给出了总数据量n=5000、10000、20000和30000时，KACA、GAA-CP和KAM-RCT中k值的变化对信息损失度的影响。如图2(a)所示，当n=5000时，本文提出的KAM-RCT算法对于任意的k值都有较低的信息损失。如图2(b)、图2(c)所示，当n=10000和n=20000时，KAM-RCT算法在信息损失度量方面依然优于其它两种算法，并且信息损失度有所降低，这是因为数据量的增加，导致聚类结果更好，匿名后等价类中的数据点更加紧凑。

图2 k值对信息损失度的影响

考虑到数据发布场景中可能涉及的表数据信息量更大，图2(d)使用30 000条数据进行实验，与其它算法相比，即使n=30000，本文算法依然保持最少的信息损失。此外，随着k值的增大，3种算法在匿名后的信息损失度也随之增大。原因在于随着k值的增大，等价类中包含的元组个数变多，那么要让这些等价类的属性值匿名后无法区分，必然导致概化程度增大，相应的整体信息损失度也就越大。

图3给出了当匿名参数k固定不变时，数据集大小n的变化对算法信息损失度的影响。从图中可以看出，KAM-RCT算法的匿名结果仍最佳，并且当k=50时，数据量在10 000和20 000左右，聚类效果较好，信息损失度较低。

图3 n值对信息损失度的影响

比较n值和k值均相等时的信息损失度，本文提出的KAM-RCT算法的信息损失始终低于KACA、GAA-CP算法，这是因为本文算法重在优化等价类的划分过程，每一个元组的添加都按照相似性最大原则，充分考虑到数据集中离群点的存在,根据约束阈值筛选出表现较好的集群，从而使得划分完成后的等价类相似性更高，匿名化所造成的信息损失更低，有效提高了数据质量。GAA-CP算法得到的聚类结果依然对离群点敏感，相较于本文聚类效果较差，信息损失较高；KACA算法对预定义的属性概化层次树过分依赖，易导致过度概化的情况发生，故信息损失度偏高。

3.3 执行时间分析

为进一步比较分析KAM-RCT算法在执行时间上的特点，我们分别进行了以下2组实验。第1组实验保持数据量大小n值不变，考察3种算法在不同匿名参数k下的执行时间变化，图4中的4张图分别给出了数据集大小n=5000、10000、20000和30000时，KACA、GAA-CP和KAM-RCT中k值的变化对执行时间的影响。由图4不难看出，KACA和GAA-CP的执行时间均起伏变化不大，且一直保有KACA>GAA-CP。因为在一般情况下，随着k值的增长，构造单个等价类所需的时间会随之增长，但由于元组总数固定不变，划分出的等价类个数也会相应减少，因此算法的总执行时间变化不大。

图4 k值对执行时间的影响

如图4(a)所示，当元组个数较小时，KAM-RCT算法的执行时间始终明显优于其它两种算法。由图4(b)～图4(d)可知本文提出的KAM-RCT执行时间随着k值的增大而不断减小，且k值越大相较于其它两种算法在执行时间方面的优势也越明显。原因在于KACA和GAA-CP算法聚类过程迭代次数过多，而本文的算法致力于优化群集过程，通过排除离群数据，大大降低了聚类的迭代次数。因此，匿名参数越大，根据阈值需重新分配的簇和元组减少，等价类重新划分所需的时间也相应减少，从而提高了算法的执行效率，并使其更适合数据匿名场景。

分析算法执行时间的第2组实验结果如图5所示，固定匿名参数k=50不变，考察数据集大小在5000-30 000个元组下的执行时间变化。不难看出，随着数据表规模的逐渐增大，3种算法的执行时间也在成倍的增长，这是因为随着元组的增多，算法的总体运算量也随之增加，故时间成倍增长。此外，在n值相同的情况下，执行时间一直有KACA>GAA-CP>KAM-RCT，故本文提出的KAM-RCT相较于其它两个算法有明显改进。

图5 n值对执行时间的影响

4 结束语

针对现有的基于聚类的k-匿名隐私保护方法对离群点敏感问题和匿名后数据质量较差问题，本文提出了一种基于约束聚类的k-匿名隐私保护方法。该方法通过KNN分类思想划分初始集群，并根据设定的信息损失阈值δ将集群进行重新划分，划分过程始终遵循信息损失最小化原则，有效排除了离群点对聚类结果的影响，从而有效减少匿名后的数据信息损失量。实验结果表明了KAM-RCT算法的有效性，不仅提高了数据发布质量，还在执行时间和数据质量之间找到了较好的平衡。然而该算法没有对敏感属性进行约束，仍存在受到同质性攻击的风险，因此，下一步工作准备从敏感属性入手，设计一种能够实现大量动态微数据的匿名算法。