基于数据冗余性的近似计算技术

陈折桂，王 晶,2+，张伟功,3

(1.首都师范大学 信息工程学院，北京 100048；2.首都师范大学 北京成像理论与技术高精尖创新中心，北京 100048；3.首都师范大学 电子系统可靠性技术北京市重点实验室，北京 100048)

0 引 言

伴随着神经网络应用范围的扩展，近年来涌现出了大量针对不同需求的机器学习框架[1-3]，用于处理现代社会爆炸式增长的信息和数据。随之而来的是数以千计的计算机组成的数据中心，为机器学习框架的执行和数据的处理提供算力支持。然而，爆炸式增长的数据使得数据中心所需的计算成本更加昂贵，存储墙问题更加严重。有限物理存储容量限制了训练的规模和推理的速度。

压缩方案是应用广泛且实施简单的拓展有限存储容量的方法，然而这些只能对特定特征的数据进行压缩的无损方法会在压缩解压缩的过程中带来很大的开销。针对存储墙和高开销问题，本文提出一种基于数据冗余性的近似计算技术(redundant data approximation)，主要贡献如下：

(1)提出基于神经网络中冗余数据存储特征的冗余数据近似算法，针对权值矩阵稀疏化、输入数据重复化等不同的冗余模式选择压缩算法，针对相似数据小范围浮动型的冗余模式选择近似算法，提高数据存储密度。

(2)针对神经网络的结构设计了支持拓扑感知的冗余数据近似算法，根据不同的网络拓扑，冗余数据近似算法能够寻找到较为优化的近似方式，进而提高压缩效率和计算效率。

(3)实验结果表明，采用本方案近似压缩率平均达到了51.38%，为提高数据密集型应用的系统加速比提供了广阔的可行性。

1 研究动机

为克服神经网络训练的内存容量瓶颈，理想化的解决方案就是让访存和搬运数据所需时间等于计算所需要的时间，如式(1)

(1)

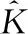
目前典型的压缩算法包括：ZCA(zero-content augmented)压缩，该算法针对的存储数据值大多为0，或NULL；FVC(frequent value compression)压缩，该算法可将存储的大量重复数据进行压缩，以此减少源数据所占的空间；FPC(frequent pattern compression)压缩试图把几种可压缩的模式进行压缩，比如4位符号扩展，8位符号扩展等。这些压缩算法都能够保证无损压缩，但是都只能对特定特征的数据进行压缩，对其它数据特征无法进行有效压缩，并且压缩解压缩过程中带来的开销很大。传统的无损压缩方法能够消除冗余数据提高系统性能，然而对于神经网络应用，其自身具有一定的错误容忍能力，对于结果要求并不那么精确，神经网络的冗余数据以及对不精确结果的可容忍性为降低无损压缩带来的压缩和解压缩等额外开销提供了可能。

神经网络的容错特性使得其可以接受近似计算的存在。近似计算利用了应用程序对不精确结果的容忍度和用户的感知限制，放松了对精确计算的要求，实现了计算精度与能效的折中。在很多既具有冗余数据又具有容错能力的新兴领域中，如图像和声音处理、计算机视觉、数据挖掘等得到广泛应用。近似计算技术通常分为两类，基于软件的近似计算技术和基于硬件的近似计算技术。软件近似机制通过对应用程序的特殊代码段近似执行来达到减少计算开销的目的[5]。基于硬件的近似计算又可以大致分为基于计算的近似和基于存储的近似。基于存储的近似可以探索存储器体系结构中的数据相似性，如文献[6]就探索了高速缓存行之间的近似；根据高速缓存的空间/时间相关性提出的跳过一些内存访问也是一种好方法[7]。最常见的基于计算的近似就是精度缩放技术[8]，该技术在质量约束下调整操作数位宽以提高能量效率。目前针对数据方面比较常用的近似方法就是跳过内存访问和尾数截断，但它们不考虑数据本身的特性，比如尾数截断的方法，就是简单粗暴地裁减掉尾数后几位，虽然它能够相对应地减少操作数位数，但没有考虑数据与相邻数据之间的关系。针对此，本文提出的方案在处理数据时考虑到了相邻数据的相似性，在质量约束下有选择地调整操作数位宽，可以实现压缩率的提升进而显著地提高运算加速比。

2 基于数据冗余模式的近似方案

基于数据冗余性的近似计算技术方案的主要目标是实现精确度和性能的折中。为实现此目标，本方案接受拥有可近似代码段的程序和用户的资源约束作为输入，并使用针对冗余数据类型设计的优化生成具有不同精度的近似方案。图1显示了基于数据冗余性的近似计算技术方案的整体框架和运行时的整体操作。

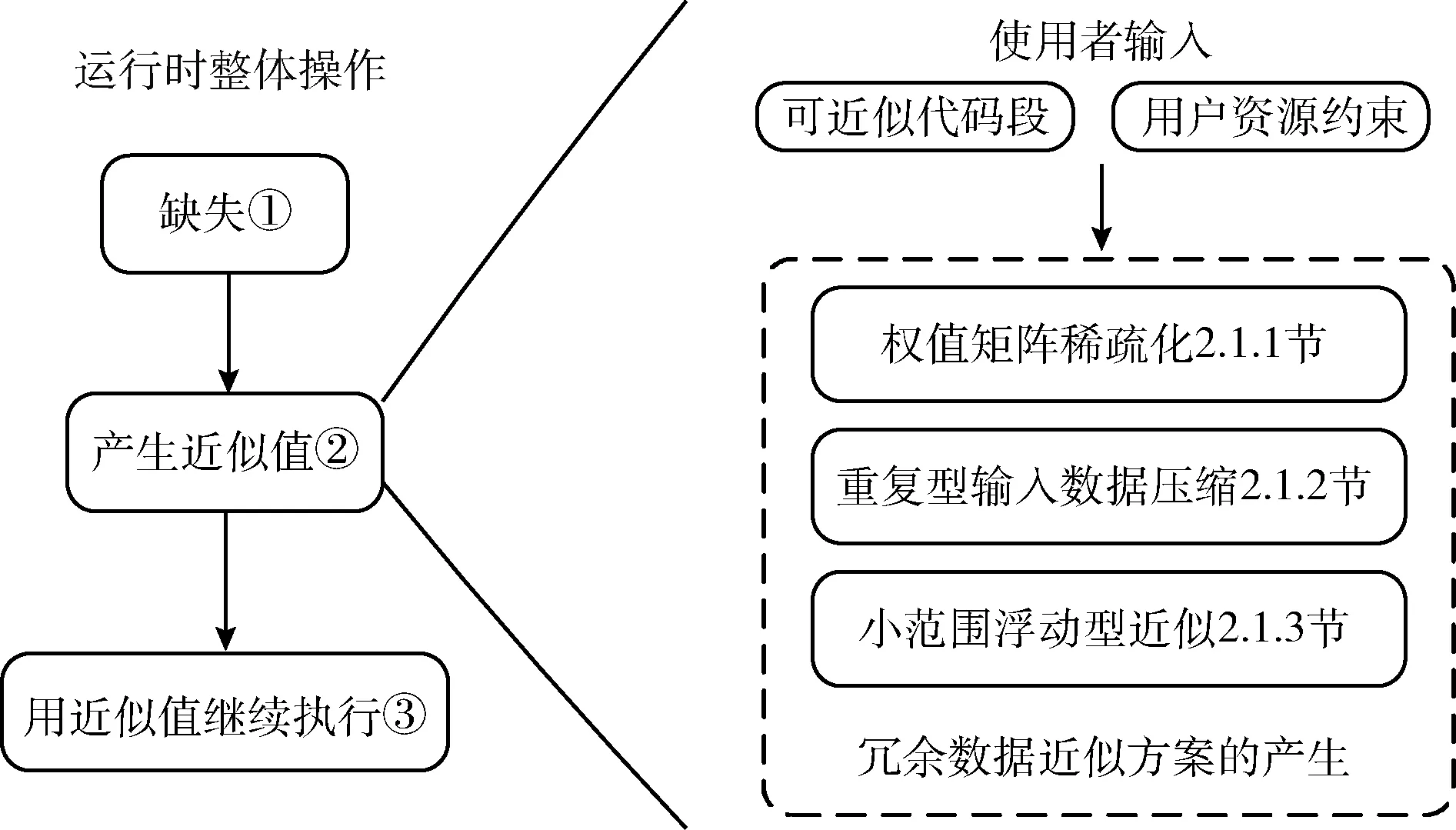
图1 基于冗余数据的近似方案概况

通过对应用程序中冗余数据模式的分析可知，常见的程序时间和空间的开销都由数据信息位的长度决定，而由于数据局部性和相似性特征，神经网络应用中的数据又存在着冗余信息，那么可以通过消除冗余信息，减少数据信息位的长度，提升数据压缩率，进而降低程序的时间开销和空间开销。因此，本文提出基于数据特征的冗余近似方案：2.1.1节描述了针对稀疏矩阵这种数据存储特征的冗余数据处理方案；2.1.2节描述了针对输入数据中重复型数据的处理方案；2.1.3节展现了近似值的产生，根据分析神经网络中相邻数据间的相似数据小范围浮动型而得到的冗余模式，选择相应的近似算法；2.2节描述了具有神经网络拓扑感知的冗余数据近似计算技术，展现了本方案在不同网络结构下的应用。

基于数据冗余性的近似计算技术通过将冗余数据消除和近似以便在缓冲区存储更多数据，一方面提高系统运行加速比，另一方面消除从存储器检索数据的等待时间和能量。在传统的存储系统中，会经常性发生未命中后从存储器层次结构中的下一级获取。而在本方案中，对于可近似代码段中的输入数据近似后存放在缓冲区中，能够在相同的容量下存放更多的数据，从而消除一定的缺失率。之后取出近似值，处理器假定这是实际精确值并继续执行。

2.1 数据的近似存储

神经网络中存在大量的输入和权值数据，输入和权值的变化都可能会导致输出质量的变化。神经网络中同样存在大量利于近似的规整数据，例如大量的0值，重复型数据以及数据差值范围浮动较小的相似数据集。现有冗余数据消除算法只针对具有某一种数据特征的存储块进行设计，难以灵活高效处理不同特征的数据，为提高压缩率，本文提出针对不同数据冗余模式的近似消除技术。图2为形式化算法流程，其中，将近似代码段的输入数据值视为一组固定大小的值的集合(如8/4/2字节)，按固定大小依次比较，匹配冗余模式，当为稀疏型时仅保留一个零值，其余舍弃；当为重复型时，仅保留一组重复值，其余舍弃；当为小范围浮动型时，仅保留基值。成功通过匹配近似并且存储长度最短的保留值即为近似值用以计算和存储，而未能够匹配到冗余模式的输入数据则视为不可近似，直接使用真实值进行计算和存储。

图2 数据近似存储策略的形式化算法流程

2.1.1 权值矩阵稀疏化

首先是针对于稀疏矩阵型冗余数据的消除。在神经网络中，其权值矩阵中存在大量的0值，如图3所示，去除冗余权值，将稠密权值矩阵(图3(a))转换为稀疏矩阵(图3(b))。之后计算输出元素时会去掉零权重的乘法累加操作，使得整个操作过程中计算操作数减少，并且能达到存储空间的降低。针对于稀疏矩阵中0值的冗余，本文提出的方案是只需存储一个数值。

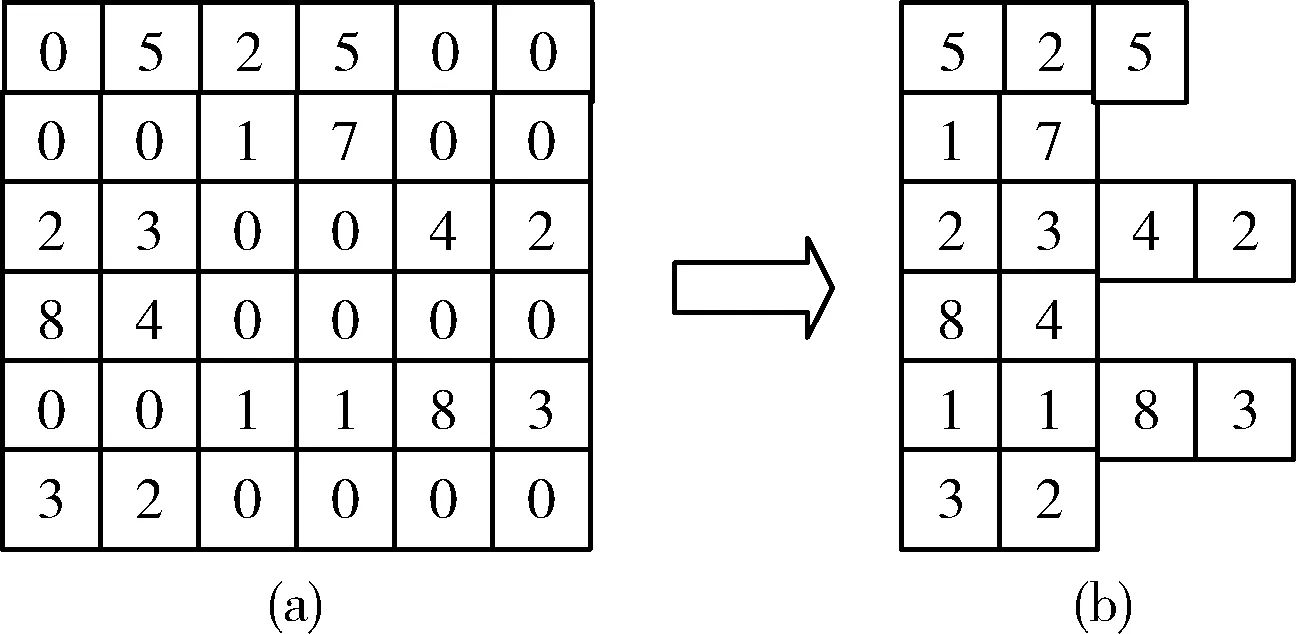
图3 稀疏矩阵性冗余数据的处理

2.1.2 重复型输入数据压缩

神经网络的输入有大量的图像视频等应用，在这些应用领域中，彼此相邻的元素可能具有相同的值，于是，输入时利用一部分元素的值代替其它重复的元素值进行计算也可以得到符合要求的目标输出质量。针对于输入数据中存在着的重复数值，本文根据重复值的字节数的不同，基于数据的对齐存储特性可分为4字节和8字节重复值存储，并标记其它重复值的个数。图4反映了输入数据中重复数值的处理和复用方式，利用这种方式可以大量压缩冗余数据，提高压缩率。

图4 输入数据中重复型冗余数据的处理

2.1.3 小范围浮动型近似

实际过程中的很多应用并不需要执行完全精确的计算。一方面，精度较低的数据并不总是导致功能错误；另一方面，由于许多数据密集型神经网络应用本身具有抗错误能力，有时甚至可以恢复，其可以接受一定数量的功能错误，并且不会影响最终输出质量。因此，在此部分，我们提出了相邻数据具有近似可能性的小范围浮动相似值的近似计算方案，如图5所示。对小范围浮动值冗余模式，需要判断基值和差值。由于基值越多，算法越复杂，时间开销越大，压缩率越低，基于性能和开销的折中考虑，方案选用2个基值，一个基值为0值，另一个基值根据具体的神经网络矩阵中的数值进行选取，利用精度扩缩舍去矩阵行中的数据与基值进行向量减操作得到的增值，仅保留2个基值。由于应用程序的数据存在多样性，因而支持多种数据长度，基值可支持2字节、4字节和8字节。此方案相对于无损压缩由于舍掉增值而引入了误差，但同时，由于舍掉增值仅存储基值而使源数据信息位的长度变短，提升了数据压缩率，空间开销和延迟开销也会相比于无损压缩进一步减少，系统的运行加速比增高，同时相较于无损压缩还省去了压缩和解压缩的额外开销。另外，本文提出的方案不仅能够减少操作数位宽，还能相对应地减少操作数计算个数，进而减少神经网络中的计算量。

图5 相邻数据小范围浮动值近似

表1给出了支持的小范围浮动型数据的近似方式，小范围浮动值根据所选基值的不同，分为3种。

2.2 网络拓扑感知的冗余数据近似方案

神经网络的拓扑结构，包括层数和每层的神经元数量都可以变化。并且不同层的输入数据之间没有关联，其相似度往往较差。而针对小范围浮动值的近似技术中，近似数据的范围是影响压缩效果和网络精度的关键。例如，对

表1 近似压缩方式

于①3-8结构的网络：有3层(包含input、output和1个隐藏层)，隐藏层有8个神经元；和②4-4-4结构的网络：有4层(包含input、output和2个隐藏层)，每个隐藏层有4个神经元。两个网络隐藏层神经元数量都是一样的，此时想要近似就得考虑这些神经元相对应的数据究竟是在同一层里还是在不同层里，虽然8个数据同时在存储区，但是对于3-8的网络，这8个数据是一起使用，而对于4-4-4，是先使用前4个数据再使用后4个。见表2，如果不去分析拓扑，而是采用一个固定的范围如每4个数据一组去做冗余数据近似，那么对于3-8网络中的8个数据，每4个近似需要2个基值，相比于每8个一组不能最大化近似效果，造成时间和能量的开销；同样的，若统一采用每8个数据一组做近似，那么对于4-4-4网络，相比于每4个一组，由于两层隐藏层之间数据相似性可能并不大，在这些相邻数据之间找到的近似值可能误差会很大。这就要求近似方法能够感知网络拓扑，能根据网络的结构调整近似的范围，产生合适的冗余数据近似方案。

基于上述的分析，本文提出的网络拓扑感知的冗余数据近似方案首先会分析网络结构，确定网络的层数、顺序和每层神经元的个数，从而针对每一层节点的数量对神经网络中的各层输入数据做近似范围地划分，之后在这些范围内对数据实施2.1节所述的冗余数据近似方案。通过感知网络拓扑，可以解决对数据进行固定范围近似所带来的问题，能够更加优化压缩效果，减少网络精度的损失。

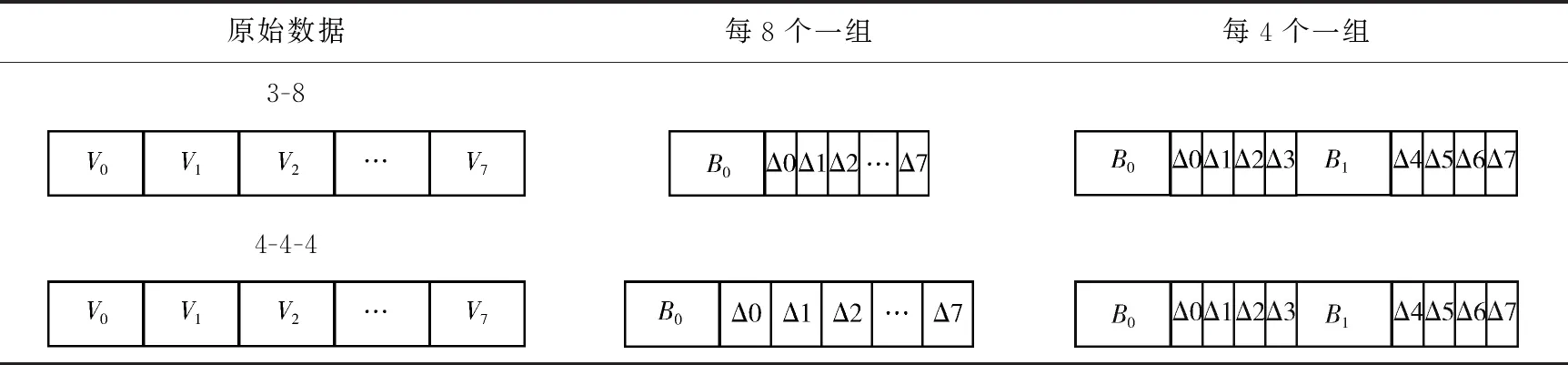
表2 网络拓扑感知的冗余数据近似方案

3 评测与分析

实验选择对比了不压缩不近似的基准方案(base)，使用收缩神经网络加速器的近似方案(SNNAP)[9]以及本文提出的冗余数据近似(RDA)方案。实验首先面向Axbench基准测试程序进行精度和压缩率的对比，其次面向神经网络应用进行评测对比，最后探索了当神经网络拓扑变化时冗余数据近似方案对神经网络应用的影响。

3.1 面向Axbench程序的评测

3.1.1 实验平台与基准测试程序

我们在sniper[10]模拟环境中运行Axbench[11]基准测试程序对本文方案进行评估。体系结构参数具体见表3。

表3 体系结构参数

Axbench是代表了现代和新兴应用并可以应用到神经网络等广泛领域的基准数据集。其中JPEG是针对彩色图像的有损压缩技术，输入是未压缩的图像，实验中让JPEG算法执行有损压缩并生成与原文件大小相比减小的类似图像。Sobel广泛用于图像处理和计算机视觉应用，在Sobel的实验中，RGB图像作为输入，最终生成边缘被重点标注的近似灰度图像。K-means是一种常用的聚类算法，广泛用于机器学习和数据挖掘，它旨在将多个n维输入点划分为k个不同的簇，使用RGB图像作为输入，输出是聚集在不同颜色区域的近似图像。FFT算法主要计算序列的离散傅里叶变换或其逆，输入是时域中的信号序列，输出是频域中信号值的近似表示。

3.1.2 程序近似敏感度和近似阈值分析

我们使用相对误差作为实验的精度测量标准。把base方案和SNNAP方案作为两个比较基准。对输入数据所能够近似的变化范围称之为近似阈值，应用程序使用者所能接受的最小输出结果精确度称之为目标输出质量。

分析JPEG、Sobel、K-means、FFT在不同近似阈值(即不同近似程度)下的敏感度研究实验，可以得到，在这些基准程序的实验中，对于每一个实验样本，当所能够容忍的近似阈值变大时，最终基准程序的输出误差也随之增大，即输出精度随之降低；反之，输出误差减小。并且通过几个基准程序的敏感度实验对比可以发现，如图6所示，像图像处理、机器学习、数据挖掘这些具有大量重复和相似数据的应用程序，其实验中的样本对于近似阈值的变化都很敏感，本文提出的冗余数据近似方案十分适用；而对于像FFT这样的并不存在大量重复相似的应用程序，近似阈值可选度非常小，输出误差也基本没变化。并且这幅图给使用者提供了一个动态的可调整的方案，以不同近似程度的实验作为支撑，程序使用者可以根据自己所需求的目标输出质量选择各基准程序在最合适近似程度下的近似方案。

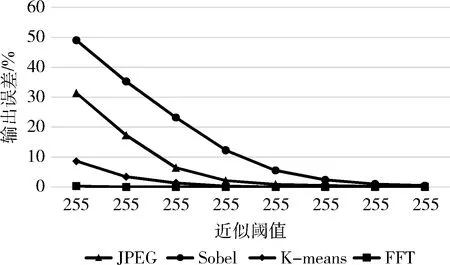
图6 各基准程序敏感度研究

3.1.3 近似效果分析

图7左侧坐标轴是base方案、SNNAP方案、RDA方案的输出质量比较。为使实验数据图表呈现最好效果，在本文的RDA方案实验中，我们对JPEG、Sobel、K-means这3种基准程序选择当近似阈值为63时的输出质量作为比较，FFT选择近似阈值为127时的输出质量作为比较。实验结果表明：在FFT的实验中3种方案相差不大，因为在FFT中并不存在大量的重复和相似数据，可压缩与可近似程度非常小，因此质量损失并没有太大变化。在JPEG实验中，RDA方案相较于base方案质量下降了6.45%，相较于SNNAP方案质量提高了2.27%；在Sobel实验中，RDA方案相比于另外两种方案质量分别下降了23.25%，提高了11.53%；在K-means实验中，RDA方案相比于另外两种方案质量分别下降了1.35%，提高了10.67%。这3种基准程序都是与图像处理、机器学习等有关的具有大量重复和相似数据的应用程序，它们的冗余数据可压缩性和可近似性非常可观，通过近似后便会产生一定的质量损失。但通过实验数据可以看到，综合来看，本文提出的方案并不会对应用程序输出质量产生大的影响，平均降低了10.35%，并且，本文的方案相较于SNNAP方案效果更好，平均提高了8.16%。

图7右侧坐标轴是使用了RDA方案后的数据压缩率的情况。近似压缩率定义为可被近似压缩的数据总量和压缩前的数据总量的比值(式(2))，近似压缩率的值越高表明压缩效果越好，系统加速比提升空间更大，带宽利用率也会随之提高。根据实验结果显示，图像处理、机器学习等应用程序的代表程序JPEG、Sobel、K-means，近似压缩率分别达到了61.88%、67.20%、25.07%，为我们提供了广阔的可行性

(2)

图7 各方案下应用的近似效果比较

3.2 面向神经网络的近似技术评测

Axbench中还引入了神经网络近似方案[9,11]，于是，我们面向神经网络应用，以该神经网络近似方案为基准方案(base)，与神经网络应用背景下的RDA方案进行比较。

3.2.1 近似效果分析

由上面的实验评估和讨论可以看到，本文提出的冗余数据近似方案对图像处理、机器学习、数据挖掘这些具有大量重复和相似数据的神经网络应用程序十分适用，因此，本小节便对这些神经网络应用进行探索与讨论，以代表程序JPEG、Sobel、K-means为例。

在面向神经网络近似环境下，通过冗余数据近似方案对神经网络应用影响的探究实验可得，敏感度和之前3.1.2节讨论的典型程序的敏感度类似，对于每一个实验样本，当所能够容忍的近似阈值变大时，最终基准程序的输出误差也随之增大，即输出精度随之降低；反之，输出误差减小。

图8是面向神经网络应用的RDA和base方案的输出质量比较。为使实验数据图表呈现最好效果，在本文的神经网络探索实验中，对JPEG、Sobel、K-means这3个程序同样选择当近似阈值为63时的输出质量作为比较。实验结果表明：在JPEG实验中，面向神经网络应用的RDA方案较于base方案质量下降了0.92%，在Sobel实验中，提高了11.56%，在K-means实验中，输出质量基本持平。通过实验数据可以看到，综合来看，面向神经网络的RDA方案不会对应用程序输出质量产生太大影响。

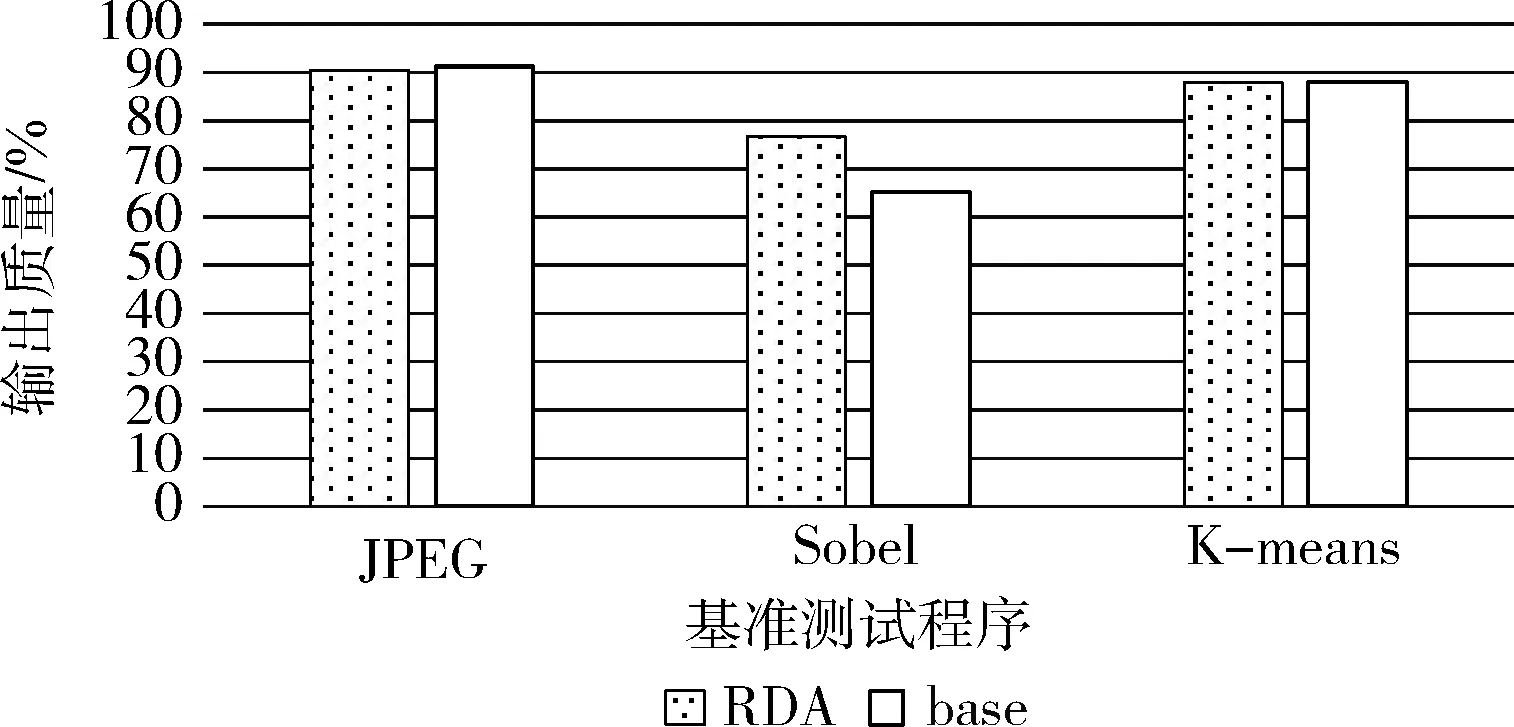
图8 冗余数据近似对神经网络精度的影响

本次神经网络探索实验中的近似压缩率也与3.1.3节的差别不大，在此不过多叙述。综合输出精度与近似压缩率，可以看到冗余数据近似方案对于图像处理、机器学习、数据挖掘这类需要神经网络处理大量重复和相似数据的应用程序十分适用，为神经网络量化加速提供了广阔的前景。

3.2.2 不同网络拓扑下近似效果分析

本小节研究内容是通过冗余数据近似方案对神经网络应用可近似区域的输入数据量化之后，探究神经网络网络拓扑的改变对输出质量的影响。图9为以JPEG为例的实验数据所绘制的结果，横坐标为不同网络拓扑结构，3-2表示神经网络最大层数为3层，隐藏层最多神经元个数是2，其余同理；纵坐标是JPEG在不同网络拓扑下的输入误差平均值。通过图9可知，无论网络拓扑变化得多复杂，面向神经网络采用冗余数据近似方案其输出误差最大不会超过1.5%，表明了本文提出的冗余数据近似方案在神经网络应用中优秀的鲁棒性和稳定性。

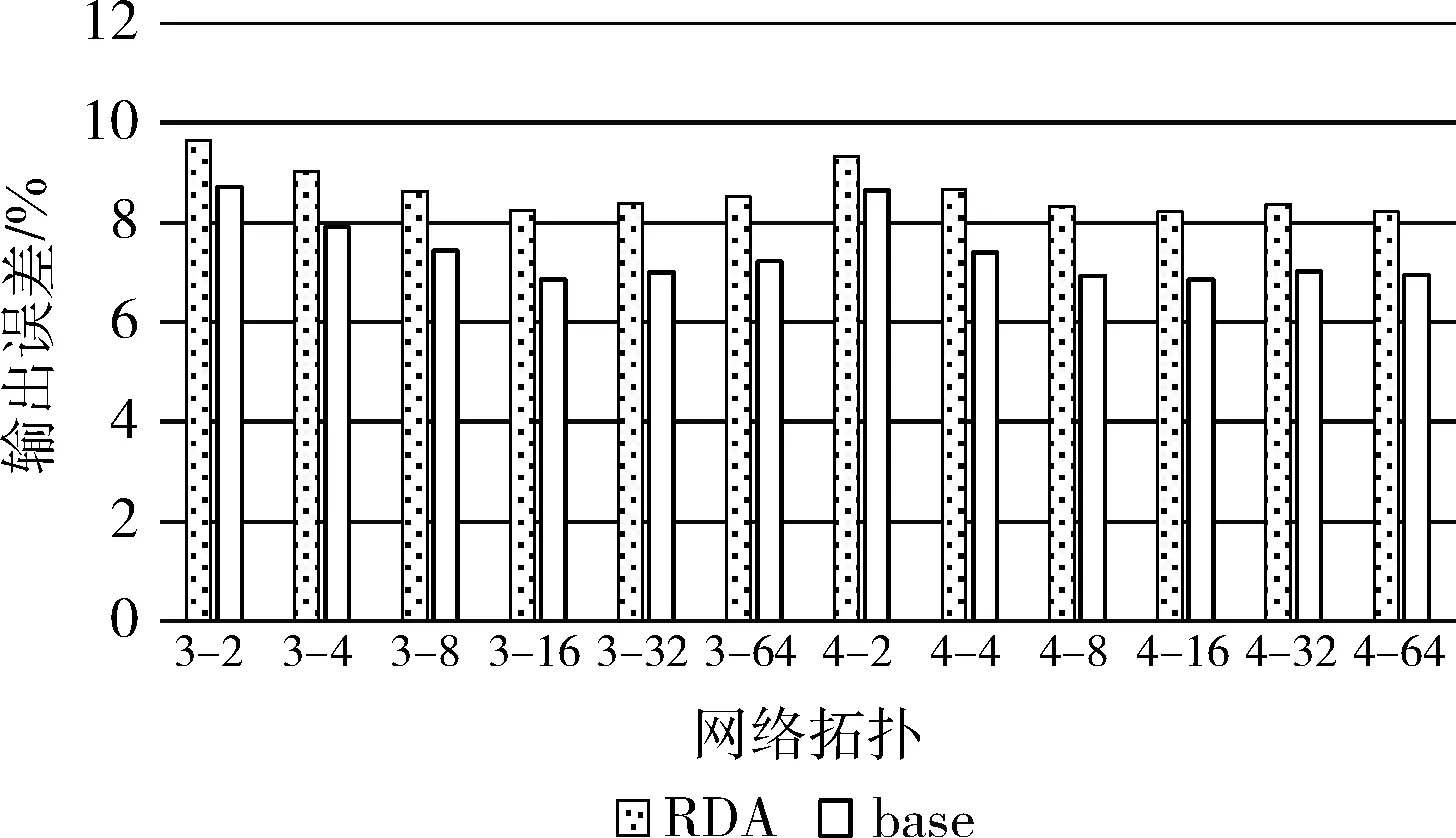
图9 误差随网络拓扑变化情况

4 相关工作

近似计算利用了应用对不精确结果的容忍特性和用户的感知限制，使得近似后的结果仍然能满足某些指标的要求。近年来提出了很多提高效能的近似计算方法，下面介绍与本文相关的近似计算技术工作。

神经网络通常过度参数化，源于在用参数表示近似模型的方式中存在着显著冗余。因此，一系列提案旨在通过减轻网络冗余来减少神经网络内存使用。特别是网络裁剪策略已经被先前文献[12,13]广泛研究。网络裁剪通过删除那些满足给定裁剪标准的冗余网络连接，可以有助于减少模型权重分配的内存。但这些提议为节省内存使用提供了有限的机会，因为权重仅占神经网络训练所需的总内存分配的一小部分。最近还有不少方案为卷积神经网络提出了一系列加速器设计[14-16]。这些先前提案属于神经网络的推理领域，而我们的工作重点是神经网络训练中的数据。更重要的是，这些先前的工作都没有解决由于神经网络内存虚拟化而产生的通信瓶颈。

除此之外，大量文献也着眼于与存储空间有关的近似所带来的性能和效率的提高。可在DRAM中支持近似存储以节省能量，当然也会带来一定的错误[17]。也有工作将寄存器中的冗余数据量[18]作为探索点，通过压缩消除寄存器中冗余数据更有效地节省能量。还有的工作着眼于精度缩放这种常用的近似技术，通过调节输入操作数的位宽来实现能量和质量的权衡[19]。

5 结束语

神经网络和机器学习框架在视觉、语言等众多应用领域发挥了重要作用，但是随着数据的爆炸式增长，计算和存储成本将变得更加昂贵，精确度和开销也难达到更好的平衡。为此本文提出了基于数据冗余性的近似计算技术，它是通过分析数据密集型神经网络的数据冗余特征，针对频繁出现的稀疏矩阵型、数据重复型、相似数据小范围浮动型这3种数据分别提出各自的压缩方案和近似方案，进而降低开销，提高存储密度。研究结果表明本文方案相比于SNNAP方案输出质量平均提高了8.16%，对拥有神经网络的基准程序进行近似和量化后输出质量平均提高了10.5%。另外，图像处理、机器学习、数据挖掘这些具有大量重复和相似数据的数据密集型应用程序更加适用于本方案，平均压缩率能达到51.38%，为提高系统加速比提供了广阔的可行性。至于未来工作还有许多问题有待进一步研究，例如如何快速有效精准地对输入数据的重要性进行评价，以达到更好的输出质量更大的压缩率，以及提高压缩率对提高系统加速比的具体影响，都值得深入探究。