基于核主成分分析的超多面体数据描述方法
陈宇晨,何毅斌,戴乔森,刘 湘
(武汉工程大学 机电工程学院,湖北 武汉 430205)
0 引 言
标注出正常数据中的异常数据的问题称为异常检测[1],通常检测任务中只有一类样本充分采集,而另一类欠采样[2-4],目前处理这一类特殊问题最常用的方法为基于数据描述的方法[5]。基于数据描述的方法主要指支持向量数据描述法及在其基础上改进和补充的方法,这些改进和补充的方法包括:利用现代优化方法对惩罚项系数和核宽度参数优化[6,7],对核方法采用扩展策略[8]以及组合多种核方法[9,10],使用其它距离表示方式代替欧式距离[11,12]等,然而这些方法无论怎样改进和补充,均无法改变其本质是通过在高维空间中训练一个超球体支撑域来描述数据,若训练样本在线性空间中极度不符合超球体时,将会产生较大分类误差。
为了给数据描述类方法提供另一种支撑域形状,在训练样本不适合使用支持向量数据描述方法时有更多的方法选择,本文提出一种基于核主成分分析超多面体数据描述的方法,该方法首先使用核方法对训练样本进行非线性映射,再利用非线性映射后样本的主成分信息构造超多面体分类器,解决了主成分分析仅能对数据线性表示的局限,实现对样本的异常检测。与支持向量数据描述法相比,超多面体具有更多的训练参数,在某些分布下,超多面体比超球体支撑域的描述更加符合训练样本。
1 多面体数据描述模型建立
1.1 问题描述及模型评价方法
异常检测问题往往可以得到大量的正常数据,异常数据出现的概率非常低,然而异常数据一旦产生,且未被正确识别将会造成很大的不良影响[13,14]。通常对未标记错误的数据进行监督学习会产生不错的模型,但数据中若混有错误标记的数据往往降低模型精度,因此本文主要对拥有标记样本以及标记样本中混有异常数据的情况建模,即对样本进行监督学习。
由于样本的不平衡性,以准确率作为评价标准的方法并不适用此类问题,对于这类问题需要同时考虑第一种误差和第二种误差。预测结果和真实结果的混淆矩阵见表1。

表1 混淆矩阵
定义精确率为P、召回率为R计算公式分别如下所示
(1)
F1分数定义为准确率与召回率的加权平均
(2)
精确率P代表正确被检索的占所有实际被检索到的比例,召回率R代表正确被检索的占所有应该检索到的比例,F1分数为两者的调和平均数,F1分数越大,表示分类正确的数量越多,当F1分数为1时,表示分类完全正确[15]。
1.2 多面体数据描述模型建立
N维空间中的一组数据可以由y1…y2N,共2N个超平面形成的超多面体支撑域完全包围,其中
(3)
式中:wi——超平面的法向量,bi——超平面的常数项。
每个yi可视为一个线性分类器,且总存在两个不同的超平面拥有相同的法向量wi,分别将其称为下界分类器与上界分类器,对于新的样本点xi,若其属于正常类,应满足
(4)
二维空间中一组样本的平行四边形支撑域如图1所示。
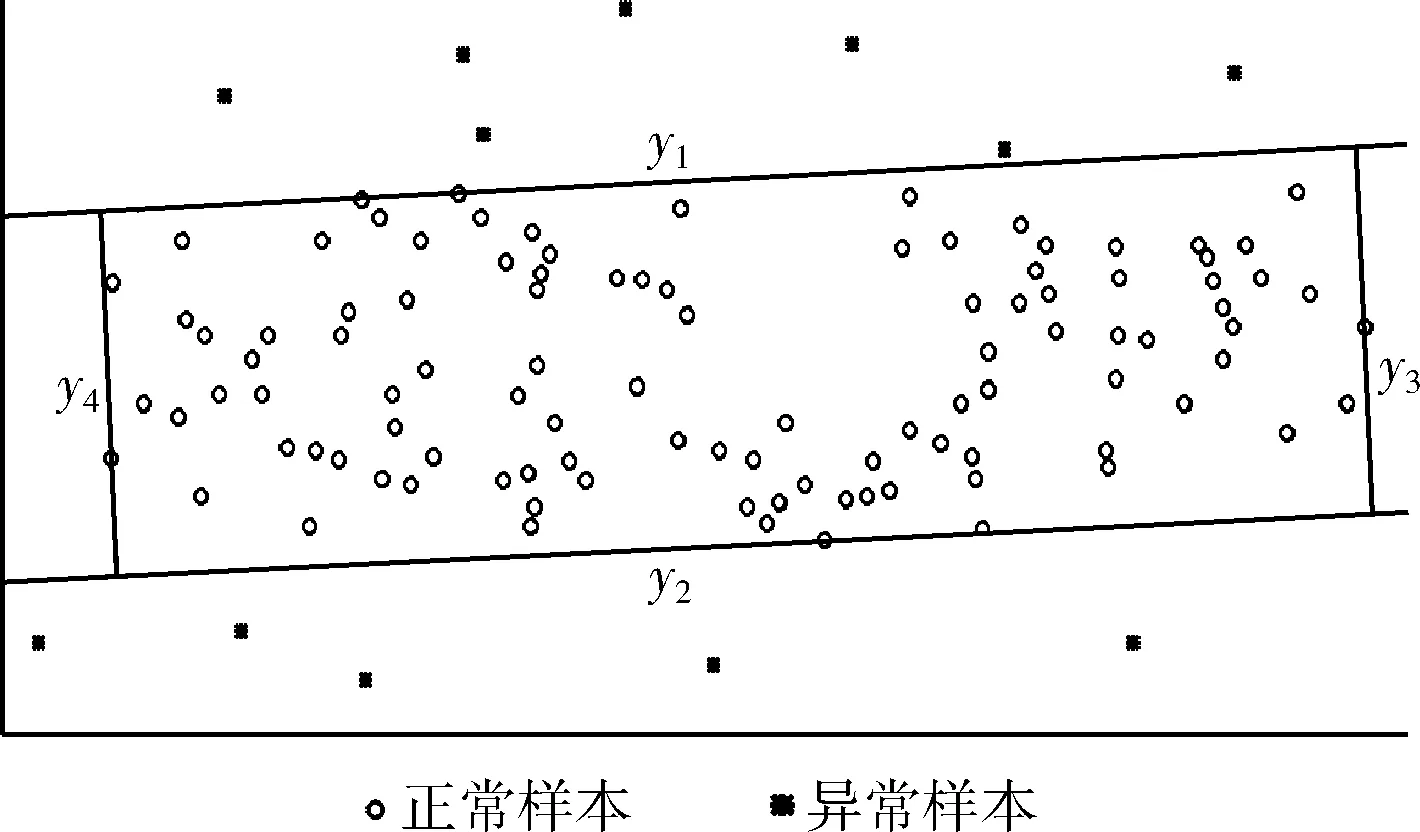
图1 二维空间四边形支撑域
图1中y2、y4为下界分类器,y1、y3为上界分类器,4个分类器组合成为一个平行四边形,当新的样本点xi落在四边形内部时则判定其为正常样本,反之则为异常样本。
对高维空间每个下界分类器ym,若已知法向量wm,bm的值可以通过以下约束优化问题求解
(5)
式中:xi——某个样本点,εi——松弛变量,C——自定义量。
与ym对应的上界分类器yn,其法向量与上界分类器的wm相同,常数项bn的值可以通过以下约束优化问题求解
(6)
由于无法保证用于训练模型的数据全为正常样本,为减少异常样本的影响可以调整式(5)、式(6)中εi以及C的值。
调整C的值对分类器的影响如图2所示。

图2 调整参数C的影响
图2为组一维数据,数据多集中在中央,中间的密度很大,向两侧密度逐渐降低,密度很低的点为异常样本的可能性大,通过逐渐减小C,越来越多的低密度点被排除,即起到了排除训练数据中异常样本的作用。
若认为用于模型训练的样本中有较多异常样本,可将C设定较小,反之则给C较大的值。
2 主成分分析及模型简化
对法向量wi的选择直接影响模型,本文使用主成分分析方法计算法向量wi,主成分分析法主要用于提取数据的主要特征,利用数据协方差矩阵的特征向量作为法向量wi,wi包含了数据间的相关信息,利用此作为法向量,得到的超多面体恰好符合数据各个方向的变化趋势。
2.1 主成分分析
主成分分析的主要思想是将空间中一组具有相关性的数据,使用其协方差矩阵的特征向量组成的基,表示原数据的坐标,消除数据间的相关性,也可将数据投影到部分特征向量组成的子空间中,实现数据的降维[16]。
主成分分析方法可以通过下面的步骤实现:
(1)计算数据每个特征的平均值μ=(μ1…μn);
(2)利用平均值μ计算数据的协方差矩阵
(7)
(3)对协方差矩阵进行特征值分解
∑=QΛQ′
(8)
其中,Q为特征向量组成的矩阵,Λ为特征值组成的对角矩阵;
(4)数据投影到N个特征向量构建的子空间
Xnew=QX
(9)
2.2 模型简化
假设特征向量组成的矩阵为:Q=(Q1,…,Qn),分别利用Qi作为模型的法向量wi,将空间中所有的数据投影到以Qi为基的一维子空间中,此时所有的数据退化为标量,训练的参数为超平面的平移量b′m,对下界分类器,b′m的值可以通过以下约束优化问题求解
stxi+εi>b′m
εi≥0
(10)
对应上界分类器平移量b′n通过以下约束优化问题求解
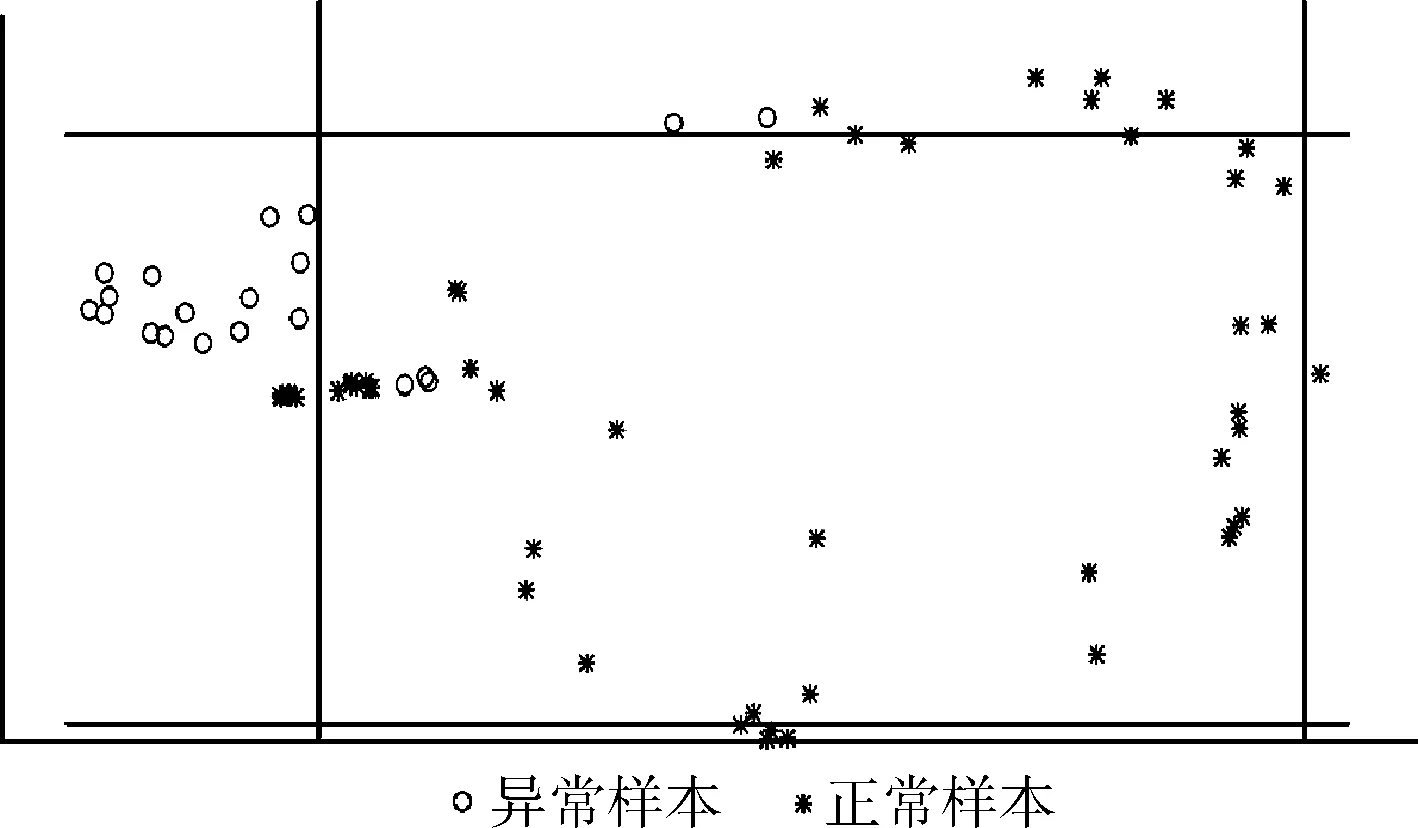
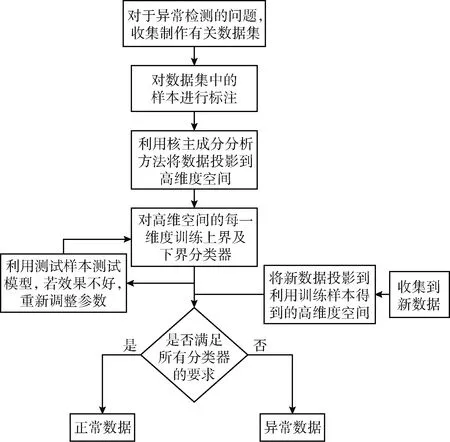
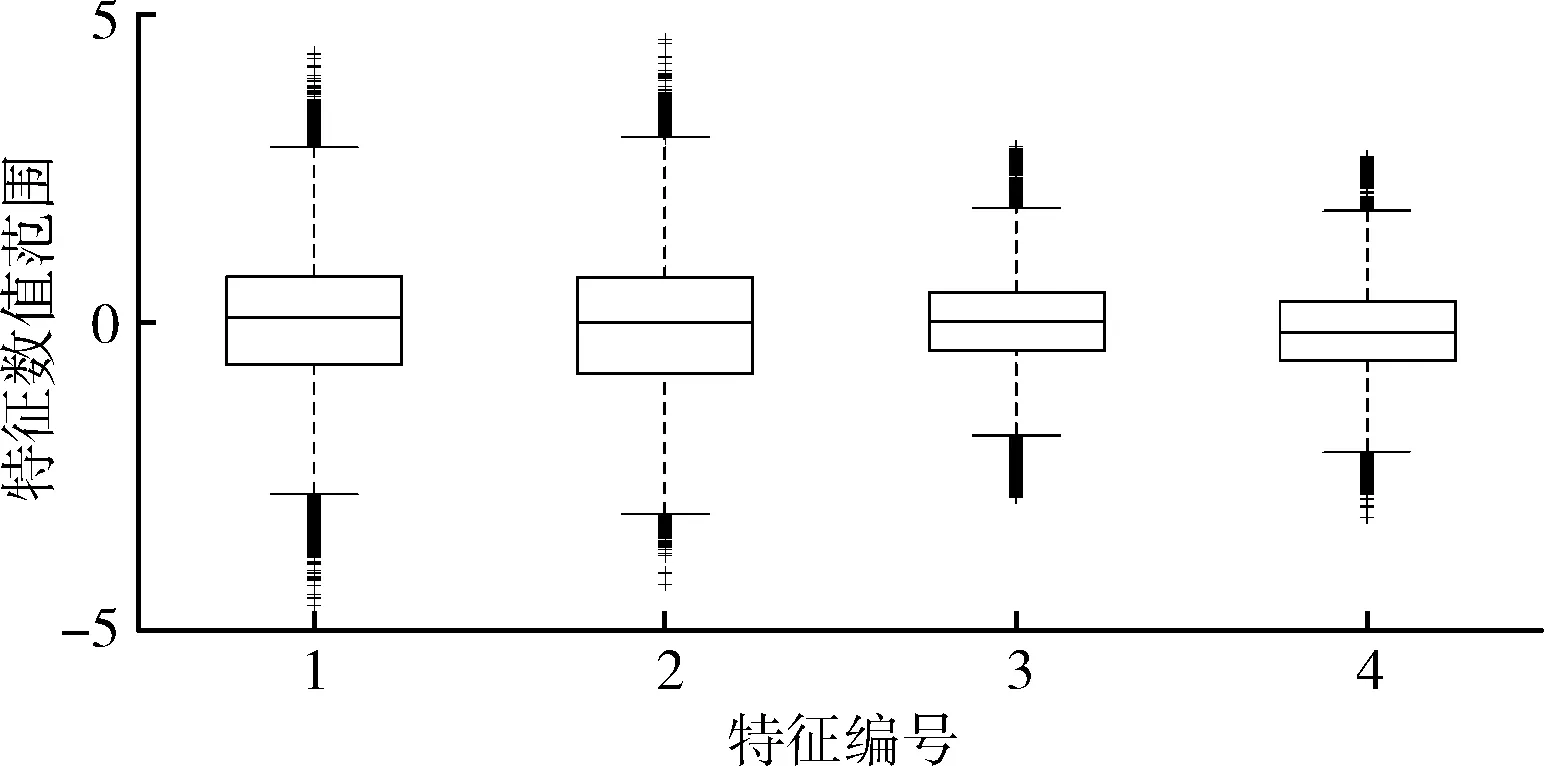
stxi-εi εi≥0 (11) 上式与式(5)、式(6)相比,约束优化问题的求解难度降低。 二维空间一组数据,协方差矩阵特征向量为Q=(Q1,Q2),数据向每个特征向量的投影及支撑域如图3所示。 图3 主成分方法训练支撑域 图3中,使用主成分法将数据分别投影到基为Q1和Q2的一维子空间中,并训练简化后的约束优化模型,得到的平行四边形支持域可以很好描述原数据,表明利用主成分的方法简化以及求解模型的有效性。 简化后的约束优化模型的平移量b′m、b′n与原模型的常数项bm、bn间的关系满足 (12) 式中:Qi——模型的法向量,但是由于式中绝对值的影响,导致了bm、bn均会求解出双值,为了避免在高维空间中对多个结果的讨论,所以采用将新数据投影到其特征向量为基底的线性空间中判断其是否为正常数据的策略,而不是显式求解出2N个超平面的方程。 主成分分析简化模型求解,并计算出法向量wi,但因为其线性特性,往往无法处理非线性数据,导致这类数据最后得到的支撑域判决效果很差,一组以异或方式分布的数据及其向特征向量投影及支撑域如图4所示。 图4 非线性可分数据的支撑域 图4中,两种数据不可被线性分离,以一种异或状态分布,使用主成分分析法建立平行四边形支撑域导致了大量异常数据被误分类。 为了解决这个问题,在主成分分析的基础上引入核方法,核方法以一种非线性映射的方式将数据投射到一个高维的特征空间里,不仅改变了数据的维度,而且使数据的某一特征得到保留甚至强化得到更好的分类效果[17]。 设Φ(·)为向高维空间的映射,对协方差矩阵的特征分解可以表示为 (13) 式中:x——数据矩阵,μ——数据矩阵特征的均值,ωi——Φ(X)Φ(X)′的特征向量,λi——特征值。 核主成分分析的一个重要定理表明:空间中的任一向量都可以由该空间的所有数据线性表示,将特征向量ωi利用数据集合Φ(X)线性表示 ωi=Φ(X)α′ (14) 式中:α——线性组合的系数向量。 将式(14)带入式(13),在等号两侧同时左乘Φ(X),得到 Φ(X)′Φ(X)Φ(X)′Φ(X)α=λiΦ(X)′Φ(X)α (15) 式中:Φ(X)′Φ(X)用中心化的Gram矩阵Kc代替,即 (16) 由于矩阵Kc为正定对称矩阵,所以存在逆矩阵,上式可进一步简化为 Kcα=λiα (17) Kc可用Gram矩阵K表示 Kc=K-KE-EK-EKE (18) 式中:E——所有元素均为1/n的Rn×n的矩阵。 计算Gram矩阵常用的核函数包括:线性核函数、多项式核函数、高斯核函数,其表达式分别为 (19) 式中:p、σ——核的大小,属于自定义量。 一般情况下,高斯核是合理的首选。第一,对比线性内核,非线性内核映射数据进入一个更高维空间,可以处理类别标签和属性之间的非线性的关系,第二,超参数的数量会影响模型选择的复杂性,而多项式内核的超参数多于高斯核,最后,高斯核将向量间的内积映射到0-1之间,而多项式核可能将向量内积映射到无穷。 (20) 将上文异或条件下的数据利用核主成分分析投影到新的二维平面上,其中核函数选择高斯核函数,新数据的位置和训练的支撑域如图5所示。 图5 核主成分分析得到的坐标及支撑域 利用核主成分分析将异或状态数据中正常数据投影到不同的高维线性空间中并训练模型,再将异常数据带入模型测试,其准确率、精确率、召回率以及F1分数见表2。 表2 各维度下各项指标 图5和表2表明在高维线性空间,异或分布的数据各项指标均值均较高,说明了核方法的有效性,将线性不可分的数据在高维空间下变的可分,训练出了有效的超多面体支撑域。 核主成分分析超多面体数据描述方法的步骤如图6所示。 图6 核主成分分析超多面体数据描述方法步骤 本文采用mulcross数据集进行实验,该数据集共有235 930组正常数据及26 214组异常数据,每个数据包括4个特征,其分布特征如图7所示。 图7 数据分析盒须图 图7表示了数据集每个特征的数据分布范围、数据的中位数、上四分位数和下四分位数以及异常数据值。 使用matlab 2015b测试本文方法,dd_tools工具箱构造支持向量描述方法。从数据集的正常数据中不放回抽取5000组正常数据作为训练集,再从剩余包含正常和异常数据的数据中抽取1000组数据作为测试集,改变空间维度,记录空间维度数及准确率、精确率、召回率、F1分数,结果见表3。 表3 本文算法各维度下分项指标 表3表明空间维度选择4以上时可以得到不错的分类效果,因此本文实验中的空间维度选择4维。 重复上述方法抽样5次,使用本文算法及支持向量描述方法利用同样的数据训练模型、测试模型,本文算法使用粒子群算法求解约束优化,两种方法均选用高斯核函数,结果见表4。 表4 两种算法分类指标结果 表4表明在所有训练数据均为正常时,本文的方法与支持向量描述方法都可以得到非常好的分类效果,且精确率均为1,说明分类时没有犯第二类错误,即没有将异常数据分类为正常数据,验证了本文方法的有效性。 当在选择训练集数据时,不放回的抽取N组异常数据以及5000-N组正常数据作为训练集,再从剩下的数据中抽取1000组作为测试集数据,当N取不同值时两种算法各项指标结果见表5。 表5 加入异常数据后两种算法分类指标结果 将表5绘制为折线图比较两种方法,折线如图8所示。 表5和图8表明两种方法的精确率均为1,分类结果均没有发生第二类错误,有效防止了第二类错误产生的不良后果,本文的方法除精确率以外的各项指标会随着异常数据混入的越来越多而下降,但即使在数据中混入10%的异常数据,依然可以得到较好的分类结果,在数据中混入2%的异常数据时,准确率依然可以达到0.945,F1分数达到0.9717,实验结果上看混入异常数据的情况下本文方法各项指标高于支持向量描述方法,验证了本文方法的稳定性。 图8 两种算法混入异常数据时各项分类指标 为了比较本文的方法与支持向量数据描述方法的时间差异,取训练集的数量为1000~5000,取样间隔为1000,记录每次训练的时间,结果见表6。 表6 两种算法时间比较/s 表6表明当训练数据的数量较少时,支持向量描述方法的训练时间略少于本文的方法,但随着训练数据的增加,支持向量描述方法需要的训练时间也随之迅速增长,当训练数量达到5000时,本文法的训练时间不到支持向量描述方法的1/10。 将该方法与支持向量描述方法应用到ODDS数据集中的thyroid数据集(共3772组数据,数据维度为6,93组离群数据),wbc数据集(共278组数据,数据维度为30,21组离群数据)、vomels数据集(共1456组数据,数据维度为12,50组离群数据)、ecoli数据集(共336组数据,数据维度为7,9组离群数据)中,两种方法的各项指标如图9所示。 图9 4种不同数据集两种方法测试 图9表明4种不同数据集测试下本文方法的效果均好于支持向量数据描述方法,利用更多的数据集再次验证了本文方法在异常检测中的可行性和有效性。 本文研究了基于核主成分分析的超多面体数据描述方法,用于解决数据中正常异常样本分布不均匀的情况下的异常检测问题,与支持向量数据描述方法相比较,本文方法不再局限于使用超球体对数据进行描述,而是为数据描述类的方法提供了另外的支撑域形状。通过实验发现,当训练数据中的样本量增多时,本文方法的时间复杂度并不会急剧上升,在一些数据集上可以得到比支持向量描述更好的分类效果,即使训练数据中混有部分异常数据时也具有一定的稳定性。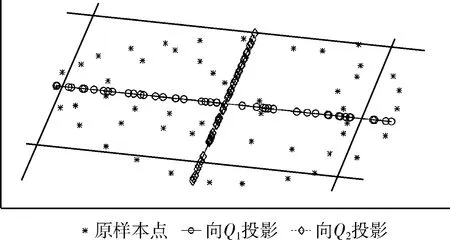
3 核方法下的超多面体非线性描述
3.1 主成分分析的局限性

3.2 核主成分分析



4 实例分析






5 结束语

