航空轴流压气机整流器周向变形分析方法研究
费 君 罗秋生
(中国航发四川燃气涡轮研究院,四川 成都610500)
1 概述
压气机作为航空发动机的核心部件,其工作时内部间隙的变化对发动机性能和结构安全性的影响很大[1]。高压转子在持续气流条件下工作时,承受着较高温度、压力和离心载荷的作用,会产生膨胀拉伸、弯扭变形,造成转子叶尖与机匣间隙逐渐缩小甚至刮伤机匣、损坏叶片,进而影响压气机工作的安全[2],国内外学者针对叶尖间隙做了大量研究[3~9]。
与转子叶尖间隙的大量研究相比,国内对压气机整流器周向变形和间隙的研究较少。但是,随着对航空发动机潜能的发掘,现在越来越重视结构的细节设计,因此,整流器扇形段周向间隙取值不能再像以前一样粗放的选择。尤其是当机匣和整流器叶片的线膨胀系数相差较大时,预留间隙不合理会导致扇形段缘板相互挤压,产生过大的局部应力,甚至产生裂纹,所以有必要对整流器扇形段周向间隙值进行分析,分析整流器扇形段的周向预留间隙值,首先就是快速、准确的计算整流器扇形段的周向变形,传统计算方法在机匣和整流器的接触位置设置困难,计算时存在非线性问题,且计算量较大。因此,本文提出了一种通过边界条件建立机匣和整流器连接关系的方法,建立了整流器周向变形计算的简化模型,并通过与传统的三维计算模型的计算结果进行对比,验证了简化后计算模型的有效性。
2 模型分析与简化
通过图1 可以看到,机匣与整流器扇形段通过榫结构连接。分析发现机匣的径向变形会影响整流器扇形段的周向空间发生变化,因此,机匣的径向变形是影响整流器扇形段周向变形的关键因素之一。同时,整流器扇形段自身的变形是影响周向间隙变化的另一大影响因素。所以,计算整流器周向变形时需要同时考虑机匣径向变形和整流器自身整体变形两方面因素。

图1 机匣整流器连接结构示意图
传统计算方法是按实际结构将机匣和整流器建立在一个三维实体模型中,计算时,在机匣和整流器的接触面建立接触单元来实现机匣和整流器的连接。这种方法可以较真实的反映机匣和整流器扇形段在实际受热变形过程中的相互关系,但是这种计算模型机匣和整流器边界位置处的网格需要特殊处理,并且划分网格时难度较大,由于机匣和整流器都是三维模型,网格数量也会非常大,导致计算量很大。这种计算模型对分析单个工况下的变形还能适用,当分析多个工况下以及过渡态工况下的变形时,这种模型较大的计算量就显得不合时宜。

图2 传统计算模型与简化后计算模型
通过观察模型的几何关系后发现,机匣上只有连接处榫槽的径向变形对整流器扇形段的周向变形产生影响;可以先计算机匣榫槽处的径向位移值,然后将机匣径向位移计算结果作为分析整流器扇形段变形时上缘板处的径向位移边界条件,通过边界条件的传递来模拟机匣和整流器的连接关系,进而计算整流器扇形段的周向变形。这种方法,分别计算机匣和整流器的变形,不需要在机匣和整流器的接触面建立复杂的接触单元,减少了计算过程中的非线性问题;同时,计算机匣变形时重点关注机匣的径向位移,机匣的径向位移可以通过二维轴对称模型计算得到,与机匣三维模型相比减少了计算量。
3 验证计算
为了验证本文提出的计算方法,以某型发动机压气机为例,机匣材料为TC11,整流器材料为GH4169,材料参数通过《中国航空材料手册》[6~7]获得,利用有限元分析软件ANSYS WORKBENCH 对简化后计算模型与传统计算模型分别进行整流器周向变形计算,并对计算结果进行对比分析。
加载相同的边界条件,对以上的两种计算模型来进行数值计算,分析它们结果的误差值,进而判断简化模型通过边界条件来传递机匣和整流器的连接关系的方法是否可行。同时,为了避免计算结果的偶然性,设置了两个工况进行计算。各边界条件的加载如表1 所示。

表1 边界条件
针对传统计算模型,在计算之前除了设置如表1 所示的边界条件之外,还需要设置机匣和整流器连接边界处的接触网格的类型,考虑到实际结构中整流器榫头与机匣接触的位置几乎不发生径向相对位移,榫头的的前安装边与机匣接触的位置几乎不发生轴向的相对位移,但是由于两者在圆周方向没有相对约束,机匣和整流器会发生圆周方向的相对位移。因此,设置以上两模型接触位置的接触单元类型为“No Separation(不分离)”。
对于简化后的计算模型,机匣为二维轴对称模型,整流器模型为三维模型,两模型在计算时单独进行计算,二者没有实际结构上的连接关系,连接关系通过边界条件传递,将机匣的径向位移计算结果作为整流器上缘板的径向位移边界条件。整流器边界条件设置时,由于没有机匣的轴向约束,需要在前端面设置一个轴向位移为零的约束。
4 计算结果比较
4.1 机匣径向变形比较。以上的两个计算模型,主要存在两点不同:(1)机匣分别是三维模型和二维轴对称模型;(2)整流器的存在会对机匣的变形产生影响。而这两点影响的大小都会通过机匣的径向变形体现出来,为了了解机匣的变形情况提取了两种计算模型在榫槽处的径向位移,图3 和图4 分别为两个不同对照组下两种模型计算得到的机匣榫槽处径向变形。
传统计算模型和简化后计算模型在工况1 和工况2 下的机匣径向位移结果如表2 所示。
在两个工况的计算结果中,都是简化后的计算模型比三维计算模型在机匣榫槽处的位移偏大,其可能的原因是在三维模型中整流器的存在对机匣的变形有约束作用,简化后的模型与实际结构相比缺少了整流器对机匣的约束,会导致机匣的径向位移比真实情况大,最终可能会导致计算整流器的周向变形比实际变形小。
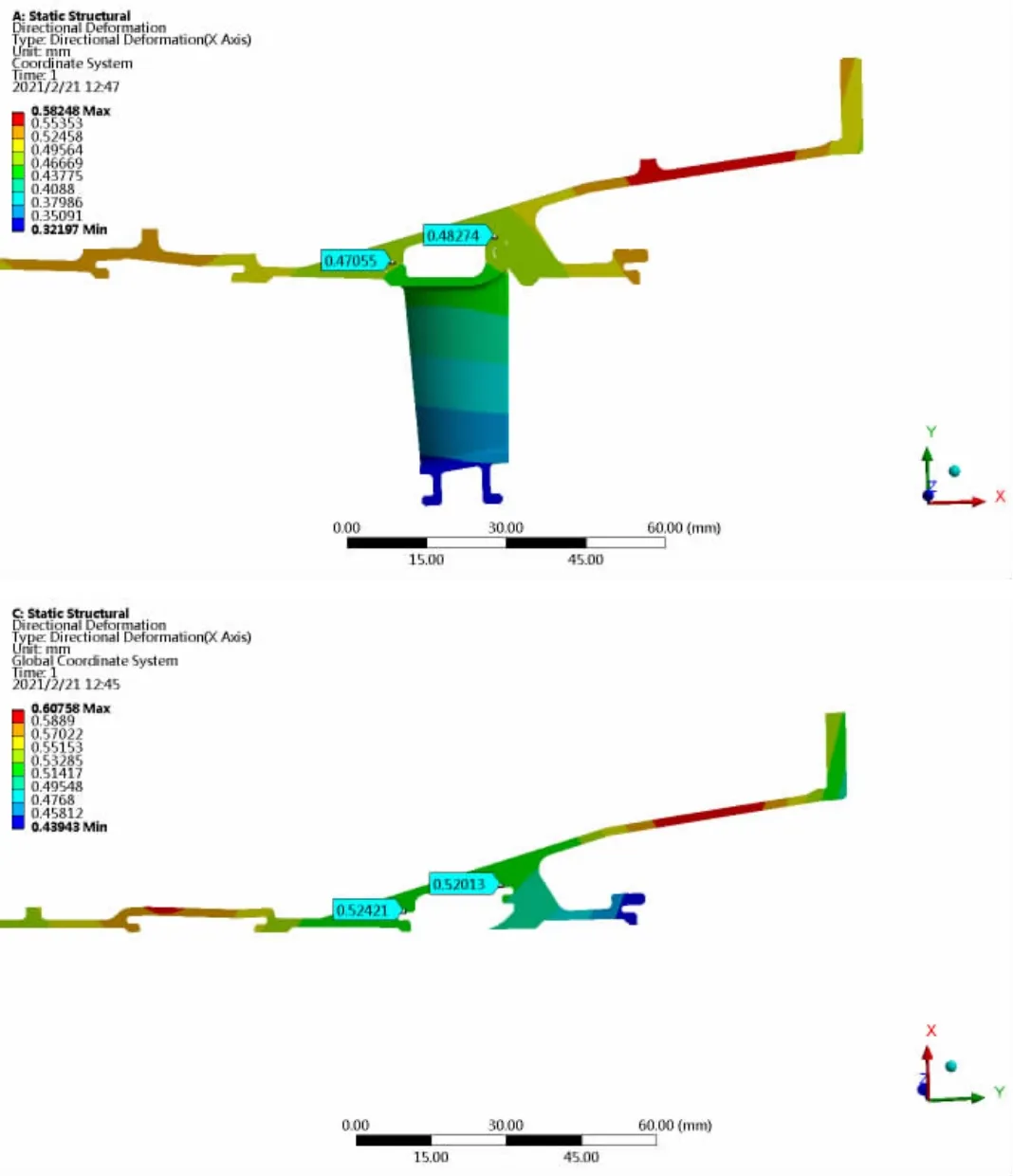
图3 工况1 机匣径向位移结果对比

图4 工况2 机匣径向位移结果对比
在两个不同工况下,两个不同计算模型在机匣榫槽处径向位移的差值分别为0.05mm 和0.06mm;通过几何关系可知,机匣变形的误差体现在对整流器周向变形的影响上,分别为0.0029mm 和0.0035mm,在工程应用中此误差可以忽略不计。因此,模型简化后导致的机匣径向变形上的偏差是可以接受的。
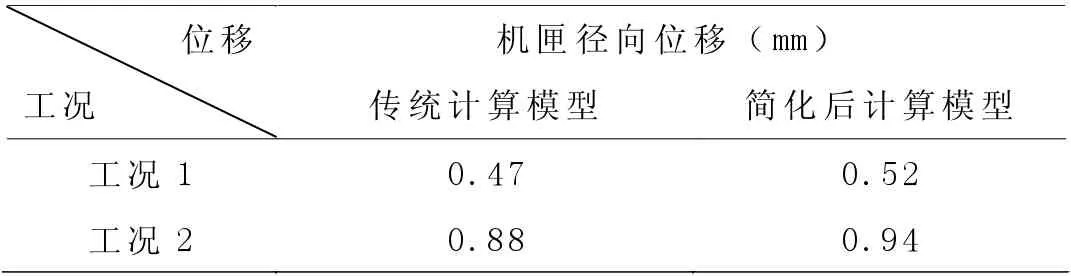
表2 机匣径向变形结果对比
4.2 整流器周向变形比较。加载工况1 和工况2 相应的边界条件,对于简化后的计算模型,还需要将简化后模型在机匣榫槽处的径向位移值0.52mm 和0.94mm 分别加载到整流器模型上,得到了如图5 和图6 所示的整流器周向变形结果。
传统计算模型和简化后计算模型在工况1 和工况2 下的机匣径向位移结果如表3 所示。
在分析机匣变形时发现,简化后的计算模型由于没有整流器的约束作用,其径向变形比实际机匣径向变形偏大,会导致计算整流器变形时简化后的计算模型中整流器的周向变形偏小,整流器周向变形计算结果对其进行了证实。


图5 工况1 整流器周向变形结果对比
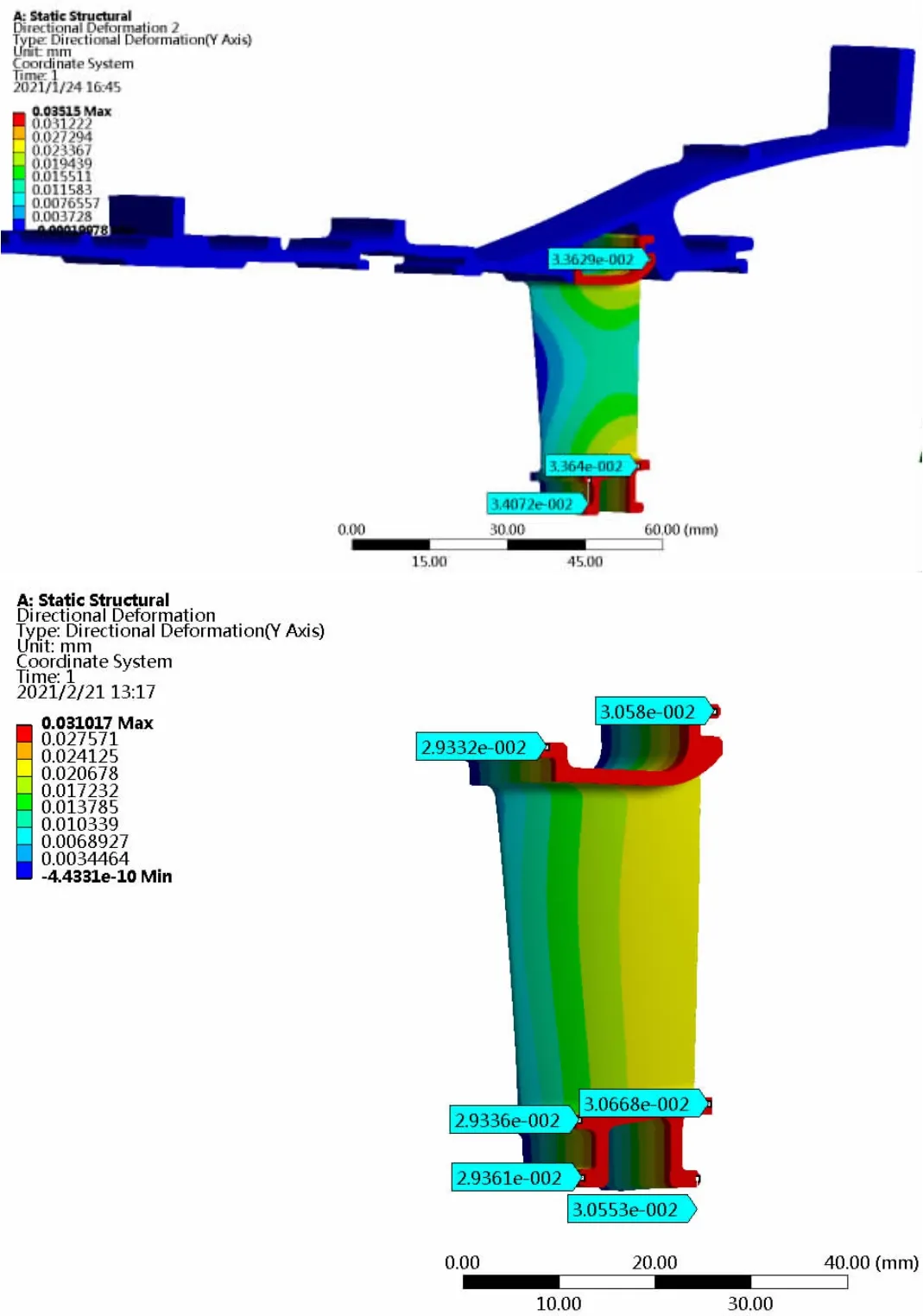
图6 工况2 整流器周向变形结果对比
在上文的分析中,在工况1 下,由于模型简化后机匣变形偏大导致的整流器变形偏小量为0.0029mm,而在整流器周向变形的计算结果中简化后的模型比三维模型整流器的周向变形偏小0.003mm,两数值十分接近;在工况2 下,由于模型简化后机匣变形偏大导致的整流器变形偏小量为0.0035mm, 而在整流器周向变形的计算结果中简化后的模型比三维模型整流器的周向变形偏小0.004mm,两数值十分接近;说明两计算模型机匣变形的误差是导致简化模型与传统模型整流器周向变形结果产生误差的原因,并且此误差非常小。
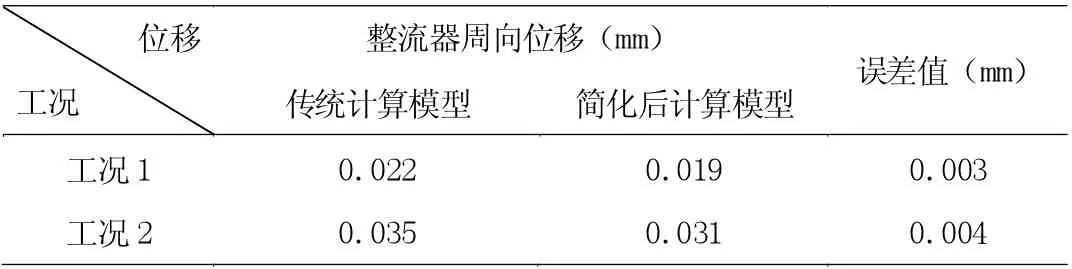
表3 整流器周向变形结果对比
通过以上的分析发现,三维计算模型与本文所提的简化后计算模型在计算整流器周向变形时误差很小,在工程应用可接受的范围内。因此,本文提出的模型简化方法是可行的,在工程应用中有实际意义。
4.3 计算耗时比较。控制三维模型和简化后模型的网格密度相同,对它们完成计算所需的时间进行记录。通过统计发现,使用简化后的计算模型所需的计算时间仅为传统计算方法的五分之一,并且随着模型复杂程度越高,所节约的计算时间越多,使用简化模型进行计算获得的收益越明显。
5 结论
综上所述,通过对简化后的计算模型与传统计算模型的对比分析,可以得出以下结论:
5.1 可以使用本文提到的简化计算模型替代传统计算模型计算整流器的周向变形,并能保证计算精度。
5.2 简化计算模型与传统三维计算模型最大不同就是没有考虑整流器对机匣的约束作用,但是其影响对计算整流器周向变形的影响很小,在工程应用上可以忽略不计。
5.3 在本文算例中,简化计算模型的计算时间仅为传统三维计算模型的五分之一,使用简化后计算模型计算可以节约大量时间。

