一类不确定半无限多目标优化问题的鲁棒逼近最优性

莫晓庆,孙祥凯

(重庆工商大学 经济社会应用统计重庆市重点实验室,数学与统计学院,重庆 400067)

设T为非空无限指标集,fi:n→(i=1,2,…,m)和gt:n→(t∈T)是局部Lipschitz函数,考虑下列半无限多目标优化问题：

半无限多目标优化问题(MP)在数学物理、工程设计、经济管理、合作博弈等领域应用广泛,目前已取得许多研究成果[1-5]. 但在处理实际问题时,由于测量等因素的影响,很难保证问题(MP)的目标函数或约束函数中所含数据的精确性. 因此,含有不确定性信息的多目标优化问题研究得到广泛关注. Chuong[6]借助变分分析工具和广义凸性假设,研究了非光滑鲁棒多目标优化问题Pareto有效解的最优性条件和对偶性定理; Fakhar等[7-8]借助一类极限次微分和一些合适的广义凸性假设条件,研究了一类约束函数带有不确定信息的多目标优化问题的最优性条件、对偶性定理及鞍点定理; Lee等[9]借助共轭函数的上图技巧通过引入一类新的闭性条件,刻画了不确定半无限多目标优化问题的鲁棒最优性条件和Wolfe型鲁棒对偶性；Chen等[10]借助一类约束标量化方法,刻画了不确定多目标优化问题的有效解及弱有效解的鲁棒最优性条件；Sun等[11]借助一类标量化方法和广义凸性假设,刻画了一类非光滑非凸多目标优化问题的鲁棒逼近Pareto有效解的充分最优性条件、Wolfe型鲁棒对偶性及鲁棒鞍点定理. 但上述研究主要针对不确定多目标优化问题的鲁棒有效解展开,而针对含有不确定参数的半无限多目标优化问题的鲁棒逼近拟Pareto弱有效解的研究尚未见文献报道.

考虑问题(MP)的不确定参数模型:

其中:ui∈Ui(i=1,2,…,m)和vt∈Vt(t∈T)为不确定参数,Ui⊆m(i=1,2,…,m)和Vt⊆q(t∈T)为不确定集合;fi:n×m→(i=1,2,…,m)和gt:n×q→(t∈T)为局部Lipschitz函数. 本文若无特殊说明,记

本文借助鲁棒优化方法刻画问题(UMP)的鲁棒逼近拟Pareto弱有效解的必要和充分最优性条件. 首先引入问题(UMP)的鲁棒对应模型:

然后通过引入一类新的广义凸性假设条件并借助文献[12]引入的鲁棒型次微分约束规格分别刻画问题(UMP)的鲁棒逼近拟Pareto弱有效解的必要和充分最优性条件,所得结果推广并改进了已有文献的结果.

1 预备知识

(T)∶={μT=(μt)t∈T|μt=0,t∈T,仅有有限个μt≠0};

设φ:n→为实值函数,若对任意的x∈n,存在正数L及x的开邻域N(x),使得对任意的y,z∈N(x),均有|φ(y)-φ(z)|≤L‖y-z‖,则称函数φ为局部Lipschitz函数. 对任意的d∈n,局部Lipschitz函数φ在x∈n处单边方向导数定义为

φ在x∈n处关于方向d∈n的Clarke方向导数定义为

若对任意的d∈n,φ′(x,d)存在,且φ′(x,d)=φc(x,d),则称φ在x∈n处为正则的.φ在x∈n处的Clarke次微分∂cφ(x)定义为

∂cφ(x)∶={ξ∈n|φc(x,d)≥〈ξ,d〉,∀d∈n}.

显然,若φ为凸函数,则Clarke次微分∂cφ(x)退化为经典的凸次微分,即

关于Lipschitz函数的其他概念和性质可参见文献[13].

定义1[13]设D⊂n是非空子集,x∈D,则集合D在x处Clarke法锥定义为

Nc(D,x)∶={ξ∈n|〈ξ,v〉≤0,∀v∈TD(x)},

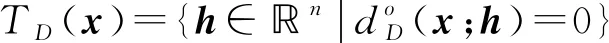
注1[13]显然,若D⊂n是非空凸子集,x∈D,则Clarke法锥Nc(D,x)退化为凸分析中经典的法锥N(D,x),即N(D,x)∶={ξ∈n|〈ξ,y-x〉≤0,∀y∈D}.

命题1[13]设D⊂n是非空子集,x∈D. 若φ:n→在x处是局部Lipschitz的,且φ在x∈D处取得最小值,则0∈∂cφ(x)+Nc(D,x).

命题2[13]若函数φi:n→(i=1,2,…,m)在n处是局部Lipschitz的,则

命题3[13]若函数φi:n→(i=1,2,…,m)在n处是局部Lipschitz的,则函数在n处是局部Lipschitz的,且

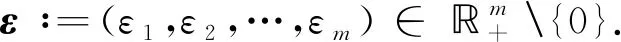
定义2问题(UMP)的鲁棒可行集定义为F∶={x∈n|gt(x,vt)≤0,vt∈Vt,t∈T}.

注2若不确定集Ui(i=1,2,…,m)和Vt(t∈T)均为单点集,则问题(UMP)的鲁棒可行集退化为问题(MP)的可行集,即F0∶={x∈n|gt(x)≤0,t∈T}.

1) 若不存在x∈F,使得

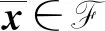
2) 若不存在x∈F,使得

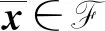
注31) 若定义3中2)的不确定集合Ui(i=1,2,…,m)为单点集,且T为有限集,则问题(UMP)的鲁棒Pareto弱有效解退化为文献[7]中定义1.1的鲁棒弱有效解.

2) 若问题(UMP)的目标函数为实值函数,即m=1,则其鲁棒ε-拟Pareto弱有效解退化为文献[12]中单目标半无限优化问题(P)的鲁棒ε-拟最优解.

3) 类似地,本文也可引入问题(UMP)的其他鲁棒逼近拟Pareto有效解,如鲁棒逼近拟Pareto真有效解. 因为其他类型的鲁棒有效解可类似处理,故本文仅研究问题(UMP)的鲁棒ε-拟Pareto弱有效解.

2 鲁棒ε-拟Pareto弱有效解的必要最优性条件

参考文献[12]引入的一类鲁棒型次微分约束规格及合理的假设条件,下面建立问题(UMP)的鲁棒ε-拟Pareto弱有效解的必要最优性条件.

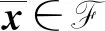
不失一般性,本文假设问题(UMP)的目标函数fi:n×m→(i=1,2,…,m)满足如下假设条件[14]:

(H1) 对任意的(x,ui)∈n×Ui(i=1,2,…,m),fi(x,ui)是上半连续的;

(H2) 对任意的ui∈Ui(i=1,2,…,m),函数x∈nfi(x,ui)是局部Lipschitz的,并且是正则的;

命题4[14]设函数fi:n×m→(i=1,2,…,m)满足假设条件(H1)～(H3),Ui(i=1,2,…,m)是m上的紧凸集,且fi(x,·)在Ui上是凹函数. 则对任意的x∈n,有

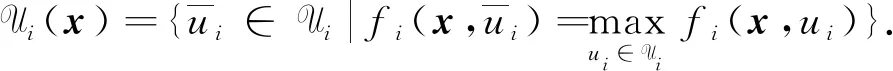
为简单,记λ∶=(λ1,λ2,…,λm)∈m.

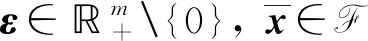
(1)

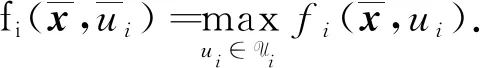
(2)

证明: 对任意的x∈F,记函数

从而

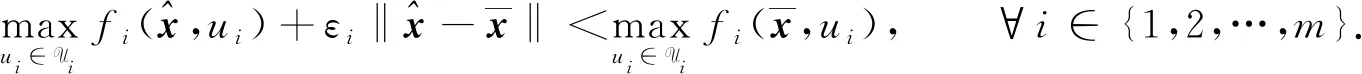
(3)

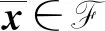
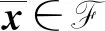
(4)

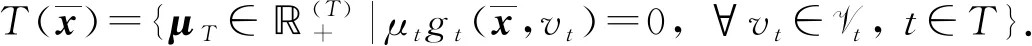
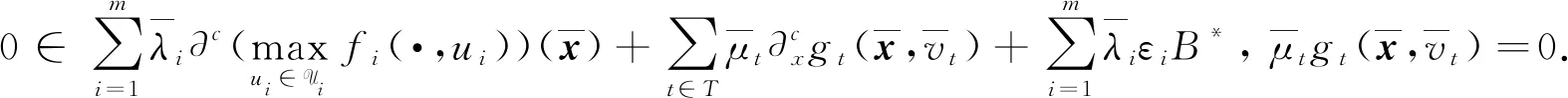
(5)

又由命题4可知

(6)

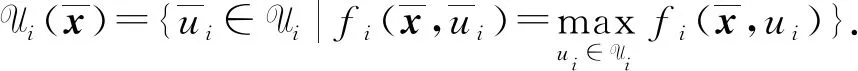
定理1刻画了问题(UMP)的鲁棒ε-拟Pareto弱有效解的必要条件.

若ε=(0,0,…,0),则有如下关于问题(UMP)的鲁棒Pareto弱有效解的必要最优性条件.

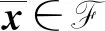
(7)

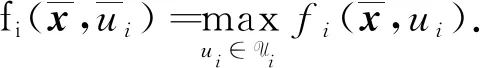
(8)

3 广义凸性假设与充分逼近最优性条件

下面借助一类新的广义凸性假设条件,给出问题(UMP)的鲁棒ε-拟Pareto弱有效解的充分最优性条件. 为简单,记f∶=(f1,f2,…,fm),g∶=(g1,g2,…,gt).

受文献[7-8]启发,先引入下列ε-伪拟广义凸性的假设条件.

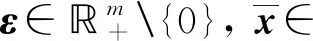
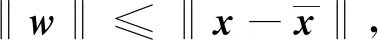
下述定理给出了问题(UMP)的鲁棒ε-拟Pareto弱有效解的一类充分最优性条件.

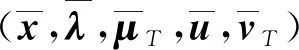
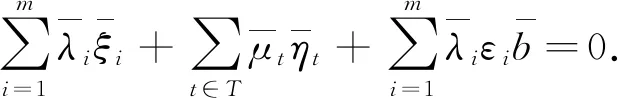
(9)

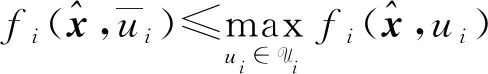
(10)

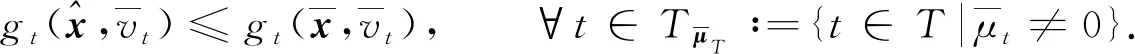
(11)

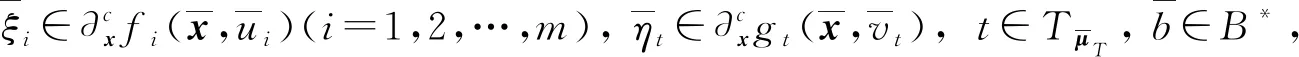
从而

若ε=(0,0,…,0),则有如下关于问题(UMP)的鲁棒Pareto弱有效解的充分最优性条件.

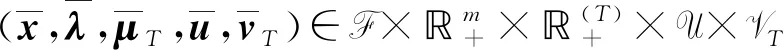
综上所述,本文从鲁棒优化的角度出发,借助一类新的鲁棒型次微分约束规格和广义凸性假设,研究了一类目标函数和约束函数均带有不确定信息的非凸非光滑半无限多目标鲁棒逼近拟Pareto弱有效解的最优性条件. 所得结果可为解决实际问题中不确定优化模型提供一定的理论参考.