鲁棒多目标规划近似拟弱有效解的最优性条件和鞍点定理
张亚萌,余国林
(北方民族大学 应用数学研究所,银川 750021)
多目标规划问题在经济、金融、工程设计、生态保护、医疗卫生和交通运输等领域应用广泛. 在实际问题中,由于受各种因素的影响,优化模型的目标和约束函数中通常含有不确定性数据,因此研究不确定优化问题有一定的理论意义. 鲁棒优化法[1]是处理不确定优化问题的有效方法之一,该方法致力于保证最坏的解不受不确定性数据的干扰. 由于多目标规划问题的(弱)有效解在非紧的情况下通常不存在,但近似解在很弱的条件下都可能存在,此外,在实际应用中利用数值算法所得的解多是近似解,因此,研究多目标规划问题的近似解有一定的价值. 本文利用鲁棒优化法讨论一类不确定多目标规划(uncertain multi-objective programming,UMP)问题近似解的最优性理论.
函数的凸性及其推广在数学规划中,尤其在建立优化问题最优性充分条件中具有重要作用. 文献[2]针对一类不确定多目标规划问题的目标和约束函数(f,g),引入了两类广义凸性的概念. 本文基于Clarke次微分对文献[2]中的广义凸性进行推广,并引入两类新的(f,g)广义凸函数的定义:(f,g)-Ⅰ型函数和(f,g)(严格)-伪拟Ⅰ型函数.
最优性条件和鞍点定理是多目标规划理论研究的两个重要内容. 文献[3-4]利用择一定理研究了鲁棒弱有效解的标量化定理和最优性条件; Lee等[5]在一种闭凸锥约束品性条件下,讨论了鲁棒拟近似有效解的最优性条件; 文献[6]综合Clarke次微分、Michel-Penot次微分、Dini次微分和Mordukhovich次微分,引入了一种非光滑次微分约束品性,并在其假设下研究了鲁棒拟近似弱有效解的最优性条件和鞍点定理. 由于近似解是拟近似解的一种特殊形式,因此,在更弱的广义凸性下,研究多目标规划问题的鲁棒拟近似解的最优性条件和鞍点定理有一定的理论意义. 本文基于Clarke次微分,在(f,g)-伪拟Ⅰ型函数条件下,建立问题(UMP)鲁棒拟近似解的最优性充分条件和鞍点定理.
1 预备知识
设A⊆n为一非空子集. 集合A的极锥[6]定义为
A°={x*∈n:〈x*,x〉≤0,∀x∈A}.


若对任意x,y∈n,λ∈[0,1],有
φ(λx+(1-λ)y)≤λφ(x)+(1-λ)φ(y),
则称φ:n→为凸函数. 若-φ是凸函数,则称φ是凹函数. 对任意的x∈n,若
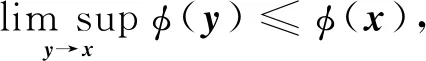
则称φ是上半连续函数.
如果存在常数L>0和r>0,满足
|φ(y)-φ(z)|≤L‖y-z‖, ∀y,z∈ B(x,r),
则称函数φ:n→在x∈n处为局部Lipschitz的,其中‖·‖表示n中的范数. 如果对任意的x∈n,函数φ在x处均为局部Lipschitz的,则称φ为局部Lipschitz函数. 设d∈n,φ在n处沿方向d的方向导数[7]定义为


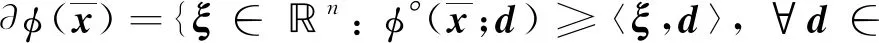
令f=(f1,f2,…,fp)T:n→p,在n上是局部Lipschitz的,则f在x∈n的广义次微分为
∂f(x)∶={(ξ1,…,ξp)T:ξi∈∂fi(x),i=1,2,…,p},
其中 ∂fi(x)为fi(i=1,2,…,p)在x∈n处的Clarke广义次微分.
引理1[7-8]令A∈n为非空子集,设函数φ:n→在处是局部Lipschitz的,且是φ在A的最小值点,则有
本文总假设Vj是nj(j=1,2,…,q)中的非空凸紧集,且满足令f=(f1,…,fp)T:n→p,g=(g1,…,gq)T:n×m→q是向量值函数,其中fi:n→,gj:n×nj→.
考虑如下不确定多目标规划问题(UMP):
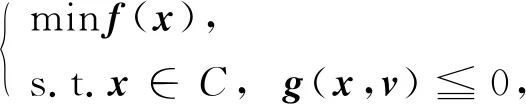
其中:C⊆n为一非空子集;v=(v1,…,vq)T∈m为不确定参数,且vj∈Vj,j=1,2,…,q. 记注意到Vj(j=1,2,…,q)为非空凸紧集,所以V也是m中的非空凸紧集.
本文用鲁棒优化法研究问题(UMP)的最优性理论,先考虑问题(UMP)的鲁棒对应问题(RUMP)[8]:

鲁棒对应问题(RUMP)称为鲁棒不确定多目标规划问题,问题(RUMP)的鲁棒可行集记为
F∶={x∈C,g(x,v)0,∀v∈V }.

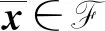
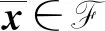
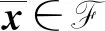
下面针对问题(UMP)的目标和约束函数(f,g),引入两类广义凸性的概念,并给出相应的实例证明其存在性.
定义2假设f:n→p,g:n×V →q均为局部Lipschitz的,称函数对(f,g)在处为Ⅰ型函数,当且仅当对任意的存在使得
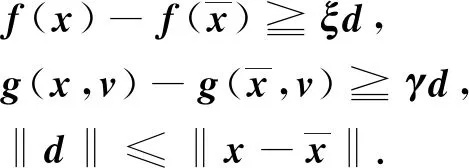
(1)
例1令f:→2,且定义f(x)=(f1(x),f2(x))T,这里
g:×V →定义如下:
g(x,v)=vx2,x∈,
其中V =[0,1],C=. 令因此有N(0;C)={0},N(0;C)°=. 易知于是对任意的其中存在d=|x|∈N(0;C)°,使得当x≥0时,有
当x<0时,有
并且总有
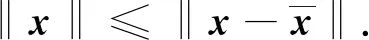
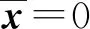

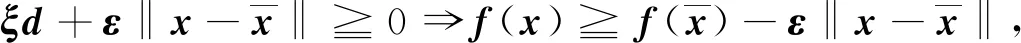
(2)


若式(2)右半部分严格不等号成立,即



例2假设f:→2,且定义f(x)=(f1(x),f2(x))T,这里
g:×V →,定义如下:
g(x,v)=-vx2,x∈,
其中V=[0,1],C=. 令因此有N(0;C)={0},N(0;C)°=. 易知令于是对任意的其中存在d=|x|∈N(0;C)°,使得
当x≥0时,有
当x<0时,有
并且有
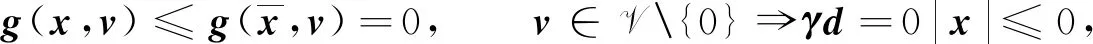
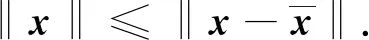

2 鲁棒最优性充分条件

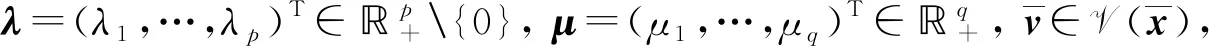

(3)

(4)
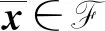
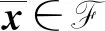
即
〈λTξ+μTγ+λTεy*,d〉≥0.
(5)




2) 类似1)的证明可得结论.



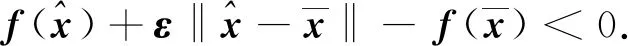

3 近似弱鞍点定理
首先,利用问题(RUMP)的Lagrange函数给出ε-弱鞍点的概念; 其次,在函数对(f,g)为Ⅰ型凸性的假设下,建立问题(RUMP)关于ε-弱有效解的鞍点定理.

L(λ,x,v,μ)=λTf(x)+μTg(x,v).
定义4令v=(v1,…,vq)T∈V,如果有

(6)

(7)

注2若在定义4中,取ε=(ε1,…,εp)T=(0,…,0),则退化为文献[9]中的鲁棒弱鞍点概念.
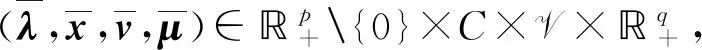



(8)
从而有
即
故式(6)成立.


因此由式(8)可得
从而有
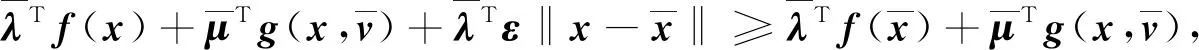
(9)
即
故结论成立.

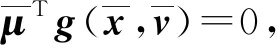
从而




