矩阵核心逆的Sherman-Morrison-Woodbury公式及其应用

杨虹 ， 钟金 ， 马柏林

（1. 江西理工大学理学院，江西 赣州 341000； 2. 嘉兴学院数理与信息工程学院， 浙江 嘉兴 314001）

0 引 言

20 世纪 50 年代，Sherman，Woodbury, Morrison等[1-4]发现了关于矩阵逆的一个公式，称为Sherman-Morrison-Woodbury 公式 （以下简称SMW 公式）。令 A 是一个 n 阶可逆矩阵，U、V 是 n×r 矩阵，X 是r 阶可逆矩阵，则矩阵

可逆当且仅当矩阵

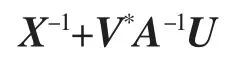
可逆。 此时，

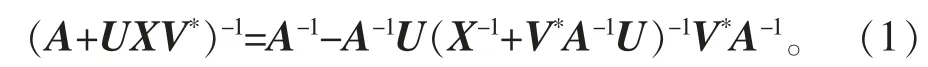
式（1）中的矩阵UXV*可以看作初始矩阵A 的更新矩阵。 SMW 公式是矩阵论中的一个重要公式，在统计学、网络、最优化、偏微分方程、线性方程组、奇异值等领域有广泛应用[5-7]。

由于SMW 公式要求矩阵A 和A+UXV*均可逆，一个更一般的问题是：当A 和A+UXV*不可逆时，各种广义逆的SMW 公式成立的条件是什么?近几十年来，众多学者研究了关于各种广义逆的SMW 公式，如 Moore-Penrose 逆、Drazin 逆、广义Drazin 逆[8-11]，并给出了这些广义逆的SMW 公式成立的条件， 但对于A-YGZT的非负性并未讨论。 本文将研究矩阵核心逆的SMW 公式， 不仅给出了矩阵核心逆的SMW 公式成立的条件，同时利用所得结论讨论了扰动矩阵A-YGZT的核心逆的非负性。

1 预备知识

2 核心逆的SMW 公式

3 扰动矩阵A-YGZT 的核心逆的非负性

4 数值例子

5 结 论

矩阵的Sherman-Morrison-Woodbury 公式不仅是矩阵论中一个重要的公式，同时在数学其他分支有广泛的应用。 本文利用值域与核的包含关系建立了矩阵核心逆的SMW 公式成立的两类条件，推广了经典的SMW 公式。 由于广义逆的SMW 公式会涉及较多的条件限制， 如何进一步弱化广义逆的SMW 公式成立的条件是值得进一步研究的问题。 此外， 本文的研究发现可借助矩阵A-YGZT的核心逆的SMW 公式来讨论其非负性，该理论也可用于研究矩阵A-YGZT的其他广义逆的非负性。