节理厚度对应力波传播和动力特性影响的SHPB 试验

李圳鹏， 何文,2， 吴贤振， 石文芳

(1. 江西理工大学资源与环境工程学院，江西 赣州341000； 2. 钨资源高效开发及应用技术教育部工程研究中心，江西 赣州341000)

0 引 言

岩石作为一种天然地质体，是岩体的主要组成部分，其内部存在着许多大小不一的细观或宏观缺陷，如节理、裂隙、孔洞等[1]。研究含平行节理岩体在冲击载荷下的应力波传播和破坏模式，有助于了解含节理岩体的动力特性，对地下工程活动具有重要意义。

王乐华等对具有不同节理连通率的岩石进行单轴压缩试验，表明节理连通率的增大，会导致岩石的峰值抗压强度也随之下降， 且试样的破坏模式也变得复杂许多[2]。 李祥龙、杨仁树等通过相似材料模拟试验的方法， 发现完整岩石模拟材料的峰值强度对应变率有很强的相关性， 但对于具有节理的岩石，节理倾角越大，其峰值强度越小，但当应变率到达一定的数值后， 节理角度对岩石破坏形态的影响不明显[3-4]。 刘红岩等采用相似材料模型试验对具有不同节理厚度的试样进行静态单轴压缩和动态冲击试验，发现随着节理厚度增加，试样强度会随之降低，但其破坏模式并没有改变[5-6]。Li 等取用矿山岩样作为入射杆和透射杆， 研究了填充节理岩体对应力波传播的影响规律， 认为节理宽度对岩体动态强度有着重要影响[7]。 李娜娜等开展了将人工切槽的花岗岩块与完整岩块组合得到不同接触面积比的节理岩块作为试样研究，发现节理的接触面积比不仅影响节理岩块的动态力学特性而且影响应力波的传播[8]。Li 等在李娜娜试验[8]的基础上，进一步研究发现应力波的传播明显受到节理吻合系数的影响[9]。 Zhou 等用LS-DYNA对含预制缺陷圆盘试样进行了数值模拟研究， 有效的模拟了试样的破坏形态[10]。 Li 等对具有一定倾角节理的红砂岩进行冲击试验， 结果表明节理角度越大，应力波的衰减越明显，吸能率与动强度呈正相关的关系[11]。 Zhang 等认为完好试样和节理试样的动强度均随应变率的增大而增大， 其对应变率的敏感性远高于节理试样， 其破坏模式也相应变得更为复杂[12]。

在已有的报道中， 对于节理岩体的动力特性研究，大多针对的都是相似模拟材料[3-6]和充填节理[13]，而针对真实节理岩体的研究鲜有报道。 对此，本文利用SHPB 装置对不同厚度节理红砂岩的动力特性进行研究，分析了节理红砂岩试样的应力波传播和破坏模式，并利用有限元软件ANSYS/LS-DYNA对试验过程进行模拟，进一步分析多种厚度节理岩体的动态试验过程。

1 试验方法与试样制作

1.1 试验方法

试验以赣南红砂岩为研究对象，研究了平行节理（与试样端面平行）的厚度和冲击速率对试样应力波传播过程中能量传递的规律及破坏形态的影响。 控制平行节理的厚度，得到 0，4，8 mm 三种情况的试样，分别对其进行动态冲击试验，并使用显式动力学分析软件ANSYS/LS-DYNA 进一步细分节理厚度，对 0，2，4，6，8 mm 五种情况进行冲击模拟，各组节理试样的试验条件如表1。

表1 各组节理试样的试验条件

1.2 试验装置

试验所需试验装置如图1， 异型冲头可以产生半正弦波， 有助于消除波的振荡和减少波的弥散效应，保证了恒应变率的加载，数据采集和显示设备为CS-1D 超动态应变仪和DL-750 示波器。 主体部分除了气压装置，其他均为高强度40Cr 合金钢，纵波波速C=5400 m/s、弹性模量E=236 GPa、直径为 50 mm，入射杆、透射杆和缓冲杆长度分别为 2，1.5，0.5 m[14]。

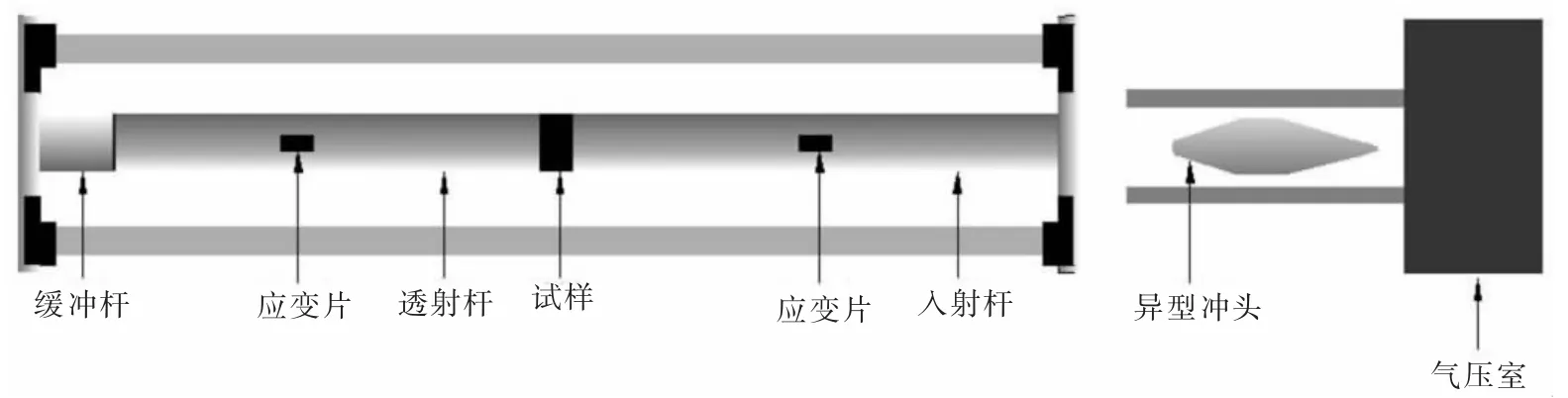
图1 SHPB 试验系统示意

1.3 试样制备

试验材料为红砂岩，选自中国赣州，红砂岩X 射线衍射谱如图2 所示， 主要矿物成分为石英、方解石、白云母和绿锥石。 先将无明显裂隙的大块砂岩加工成50 mm×50 mm （直径×高度）的圆柱体试样， 然后用钢线切割完整的圆柱体试样，使其分成两、三个部分，并用环氧树脂黏结剂黏结，将黏结好的节理试样放入模具中，防止试样在黏结过程中发生偏移。 另外，对试样两端进行磨平处理， 使其两横截面的不平行度和不垂直度均小于 0.02 mm，如图 3 所示。 R-1，2 表示完整试样，R-1-0 中R 表示红砂岩，1 表示试样序号，0 表示节理厚度， 试验红砂岩的物理力学性能参数如表2 所列。

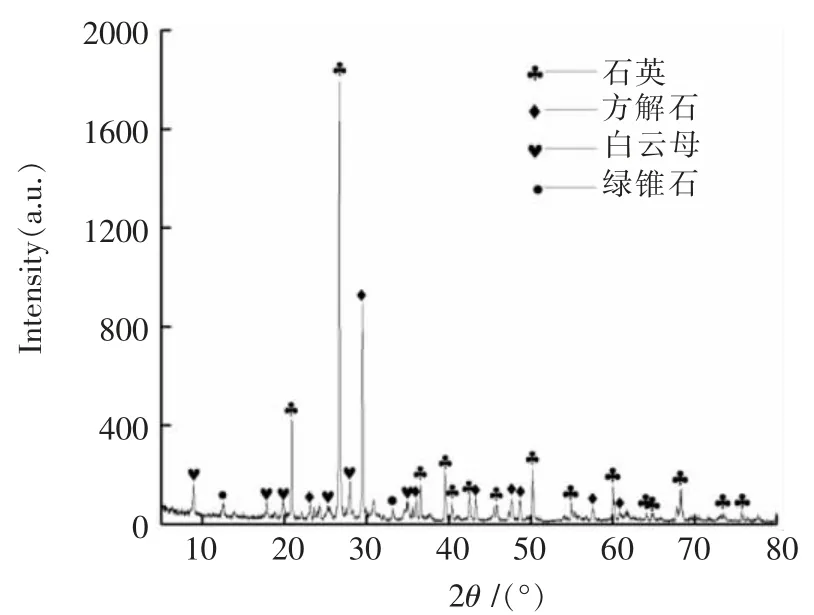
图2 红砂岩X 射线衍射谱

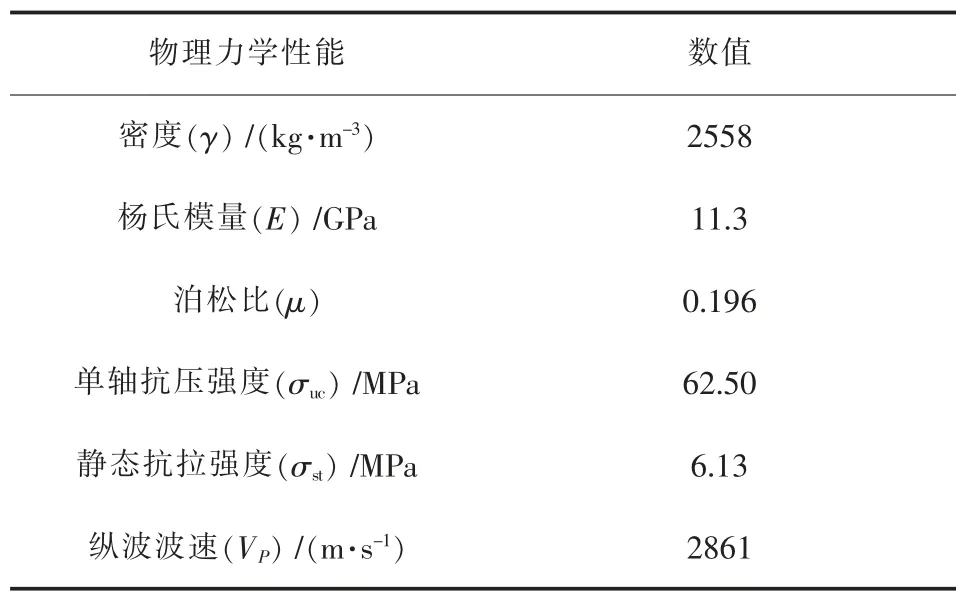
表2 红砂岩的物理力学参数

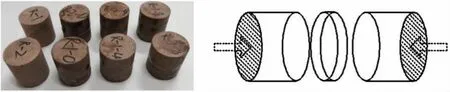
图3 不同节理厚度岩石试样及设计

1.4 应力平衡验证

在SHPB 试验中，动态应力平衡特别是宏观破裂前的动态应力平衡是使试验及模拟结果有效的关键。异型冲头在撞击入射杆时可以在杆中产生一个缓慢上升的半正弦波， 在试样中传播3 到4 次，以达到应力平衡[15]。 图4 给出了节理厚度为4 mm的试样与杆件入射与透射界面的动应力平衡，从图4可以看出入射和反射波的和与透射波十分接近。基于应力平衡和一维应力波理论，可以计算出试样的动态应力 σ（t），应变率 &（t），应变计算公式如下[16]：

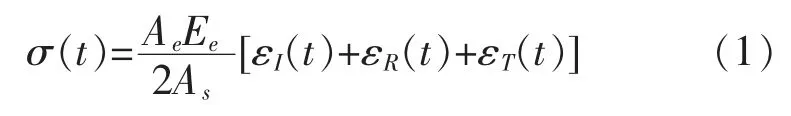
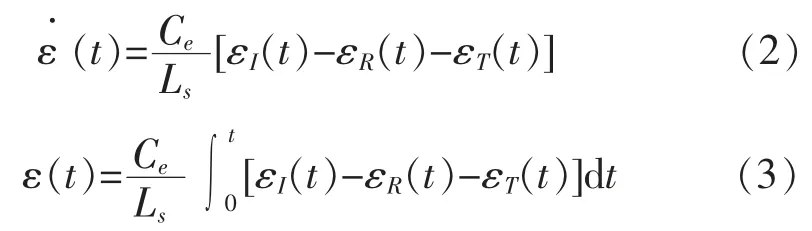
其中，Ae、Ce、Ee分别为弹性杆的横截面积、 纵波速度、杨氏模量；As和Ls分别为试样的横截面积和高度；εI（t）、εR（t）、εT（t）分别为 t 时刻的入射应变、反射应变和透射应变。

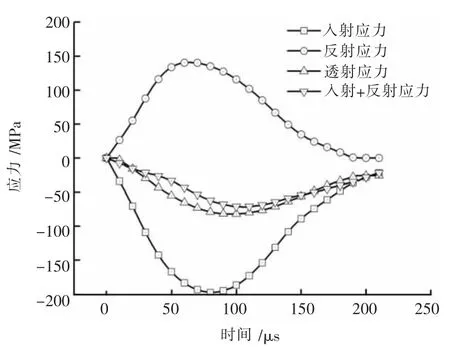
图4 试样R-2-4 的应力时程曲线

2 节理岩体的SHPB 试验数值模拟

2.1 计算模型及参数

按1∶1 实际尺寸建立有限元模型，借助有限元软件ANSYS/LS-DYNA 进行前期有限元模型的建立和计算，LS-PREPOST 处理结果模型与数据。 模型建立中， 异型冲头、 入射杆、 反射杆和试样均采用Solid164 单元建模。异型冲头前端截面直径17.4 mm，末端直径6.66 mm，中间部分直径50 mm。冲头、入射杆、 试样、 透射杆的长度分别为360.1，2000，50和1500 mm。 为了计算的准确性和更直观显示试样破坏时的单元变化情况， 将试样沿径向划分40 份，轴向划分50 份，冲头、入射杆、试样、透射杆的几何模型的单元数为 3600，15000，15000，11250，如图5所示。 由于所建模型为对称结构， 且为了简化计算，故只建立1/4 的计算模型。在x 和y 轴垂直的界面上分别施加x 和y 方向的位移约束，位移设置为0。 接触类型为自动面面接触（ 关键字为CONT ACT_AUTOMATIC_SURFACE_TO_SURFACE_）， 忽略面面之间的摩擦，接触算法为罚函数法，罚函数因子K 取2.0。 另外对于节理试样在节理处添加失效应变。试样采用的是HJC 模型[17]，其余杆件均使用线弹性模型。

2.2 HJC 模型参数

模型参数的确定决定着模拟计算结果是否正确的关键，基本参数密度γ，单轴抗压强度fc，抗拉强度T，弹性模量E 可直接通过试验测出。 由文献[18]可知，A、B 对模拟试样的峰值应力影响较大，C、N 对峰值应变影响较大。 结合文献[19-20]及试验所得参数，得到表3 的HJC 模型详细参数。

2.3 数值模拟结果及分析

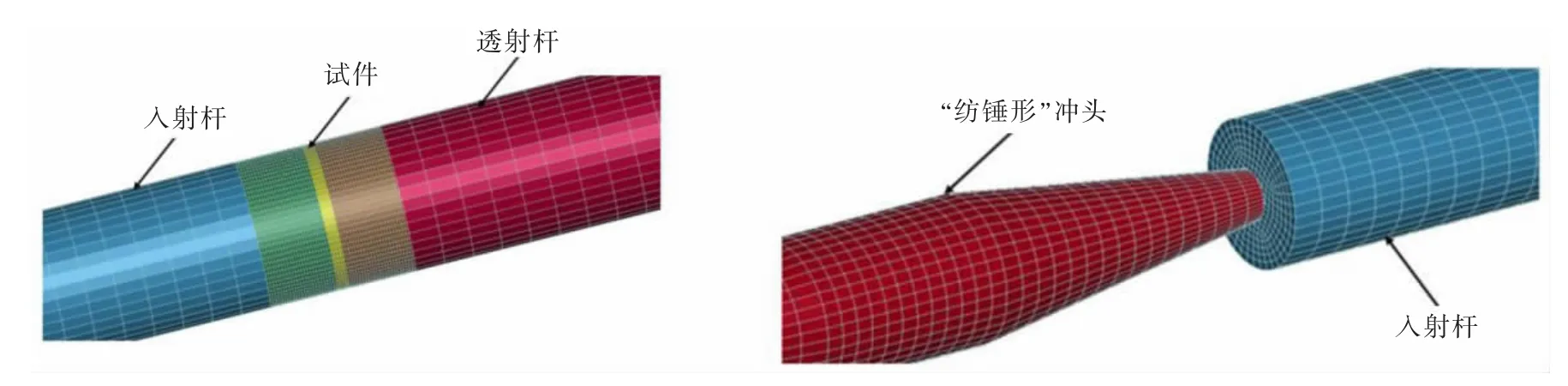
图5 SHPB 试验装置的网格划分

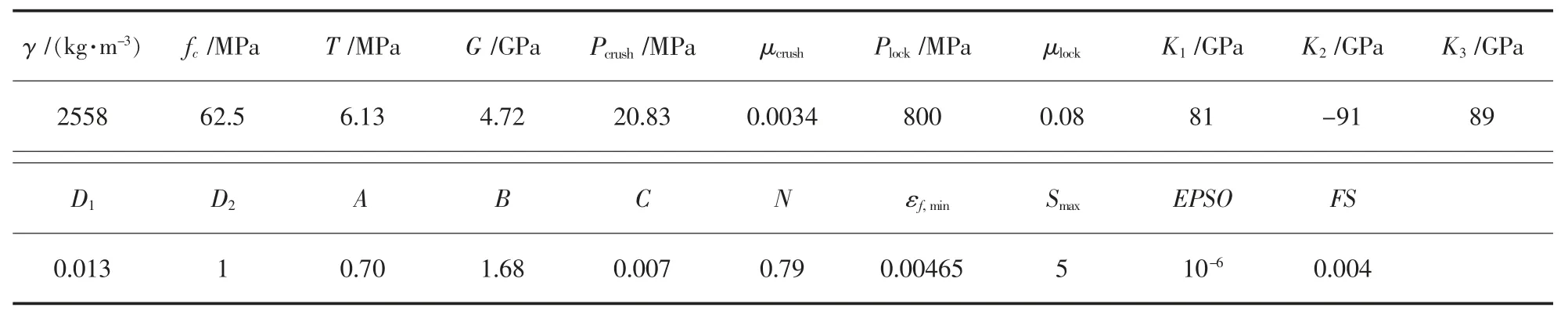
表3 红砂岩HJC 模型参数

图6 为相同速度下不同节理厚度的试验和模拟应力-应变曲线。 由图6 可知试验和模拟的应力-应变曲线具有较好的相似性， 但是模拟值的应力普遍较试验值大。 这是因为理论上，在试验中应力波在杆中的传播会随时间有一定衰减，但模拟过程中并没有这些衰减导致模拟值与试验值的差异。

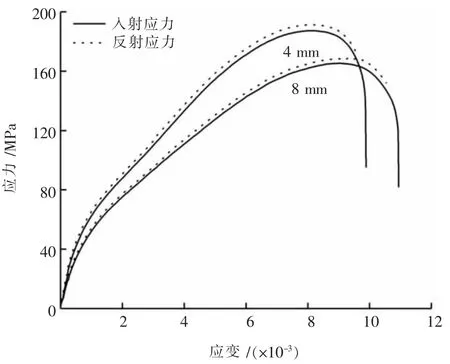
图6 不同节理厚度试样的试验曲线与模拟曲线比较

3 模拟与试验结果分析

3.1 节理厚度对反射与透射系数的影响

当应力波传播到岩石试样和弹性杆的界面时，会发生透射和反射，信号会被安装在弹性杆上的应变计记录下来。 冲击速度控制在11.09 m/s 左右变化，入射波的峰值之间没有明显差异，这一规律也可通过表4 的应变率表现出来。 反射系数Rc和透射系数Tc可由下式确定：

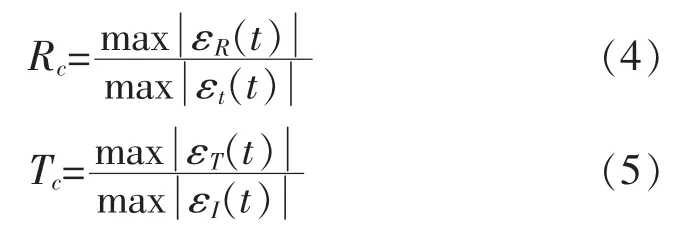
不同节理厚度下，反射与透射系数的变化趋势及函数拟合曲线如图7 所示。 从图7 可以看出，反射系数随节理厚度的增大呈线性增大变化（相关系数R2为0.98），透射系数随节理厚度的增加表现出明显的下降趋势，拟合曲线为三次函数（R2为1），与数据吻合较好，透射系数在节理厚度为6 mm 左右时达到最低值，为52.28%。 结果表明，当入射波在厚度较大的节理上传播时，波的反射越明显。 另外还可以看出反射系数的上下波动程度较透射系数更大，这是由于波在试样中预先存在的节理裂隙表面和弹性杆件及试样端面这三个不连续界面上多次反射及透射所造成的[9]。

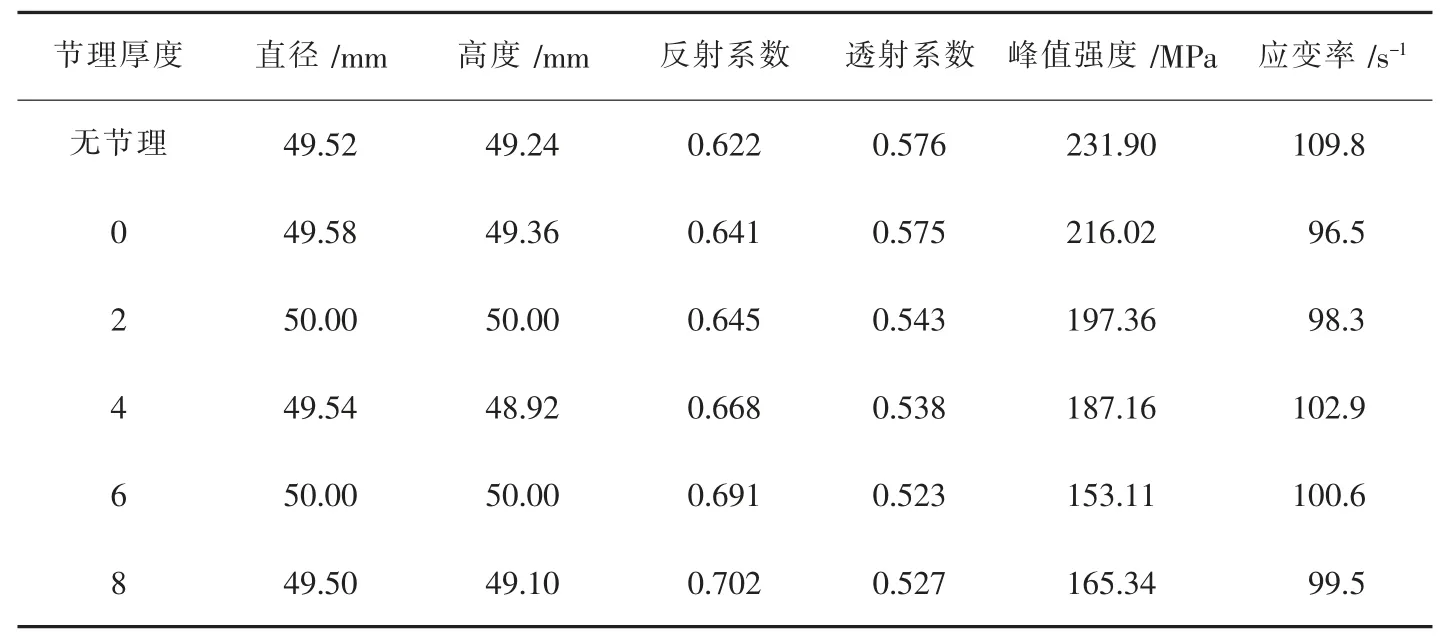
表4 红砂岩试样的应力波传播系数和动态强度

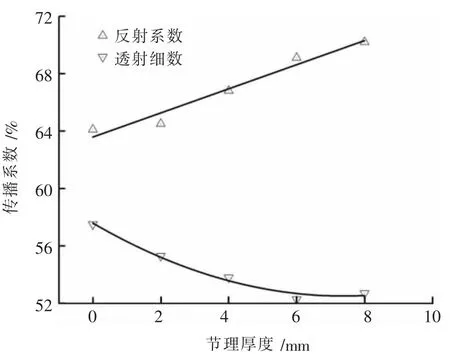
图7 不同节理厚度下的反射与透射系数

3.2 岩石动态应力-应变曲线及动态力学参数变化规律

完整和节理试样的动态应力-应变曲线如图8（a）、图8（b）所示。 由这些曲线可以看出，贯通平行节理的存在对岩石的动态峰值强度具有较强的劣化效应，完整试样在该速率下的峰值强度大约为静载条件下的4 倍， 且完整试样与节理试样的应力-应变曲线形状很相似，基本上分为4 个阶段，分别为初始压密阶段、线性阶段、非线性塑性变形阶段、峰后卸载阶段。 与岩石一般单轴压缩的应力-应变曲线相比，节理岩石与完整岩石一样，压密阶段时间跨度很短，很快进入了线性阶段。 完整试样的压密阶段要比节理试样具有更长的时间跨度，而非线性塑性变形阶段较节理试样短，峰后卸载阶段基本呈现脆性特征， 但试样R-1-4 和R-2-8 没有符合这一规律， 这可能与试样本身的离散性有一定关系， 并且R-1-4 还出现了峰后回弹现象，这表明试样还具有一定承载能力，没有完全破坏。

岩石动态峰值强度随节理厚度的变化如图8（c），在节理厚度达到6 mm 之前，试样的峰值强度呈线性降低，但当节理厚度大于6 mm 时，峰值强度呈上升趋势。 该速率下完整试样的平均峰值强度为231.90 MPa， 节理试样的平均峰值强度为153.11～216.02 MPa， 与完整试样相比动强度降低了6.87%～33.54%， 这说明平行贯通节理的存在严重影响了岩石在动载条件下的承载能力，但对于节理厚度的敏感性不同。

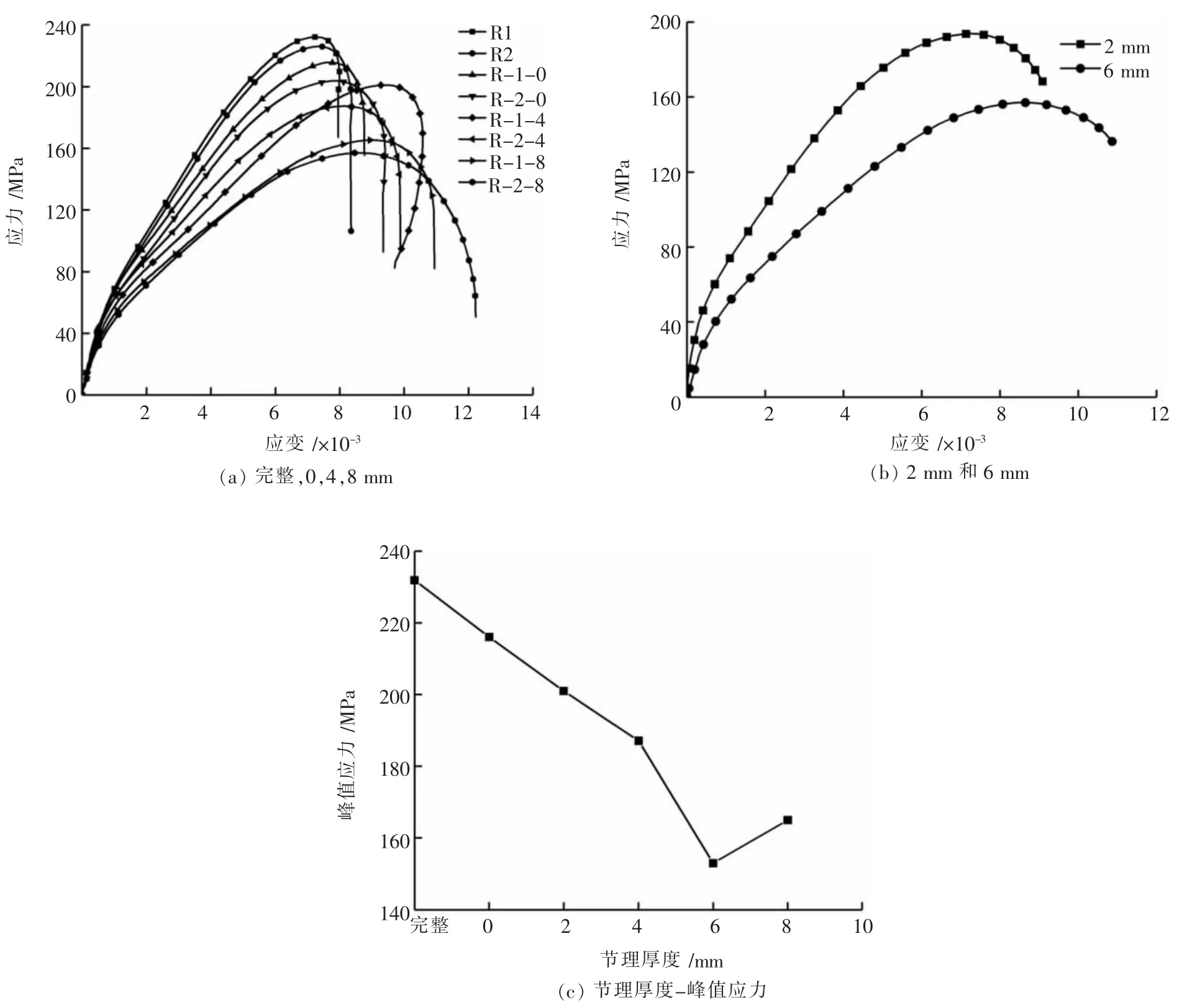
图8 不同节理厚度条件下应力-应变曲线和峰值应力

不同节理厚度下典型试样的破坏形态如图9，由图9 可以看出节理的存在对试样的破坏程度影响较大，随着节理厚度的增加试样的破坏程度越严重。节理厚度的变化并不会影响着试样的破坏形式，当节理厚度较薄（厚度＜4 mm）时，试样没有发生明显的破碎， 完整试样有宏观上的一条近似垂直端面的裂纹和一条平行端面的裂纹， 平行裂纹的产生可能是由于试样预先存在的微观裂隙所导致； 节理厚度为0 mm 的试样则有两条明显的垂直裂纹， 且都没有贯通，整体呈现张拉破坏。 随着节理厚度的增大，试样的破碎程度明显变大， 靠近入射杆一端的破坏程度较透射杆一端大， 是因为在入射波能量相近的条件下，反射系数也随之线性增大，导致反射波所携带能量占比较大， 三波叠加的峰值强度大于试样的动态抗拉强度， 使得试样下端的破坏程度较上端更严重。 当节理厚度为8 mm 时，反射波所携带能量进一步增大，导致透射波的能量较厚度4 mm 小，因此图9（c）试样的上端的破坏程度比图9（d）严重。

图9 不同节理厚度试样的破坏形态

3.3 节理岩石的能量演化特征

通过对冲击载荷过程中， 节理岩石能量消耗的分析， 可以了解岩石中的应力波衰减和动态破裂过程，从而改进能量释放方法，提高岩体的破碎效率。近几十年来，人们对单轴[21-22]、三轴[23-25]、冲击载荷[26-27]和爆炸[28]下岩石的能量特性进行了大量的试验和理论研究。在常规SHPB 试验中，入射能EI、反射能ER、透射能 ET、吸收能 ED、能量反射系数 RE、能量透射系数TE和能量吸收率R 分别为表示如下：

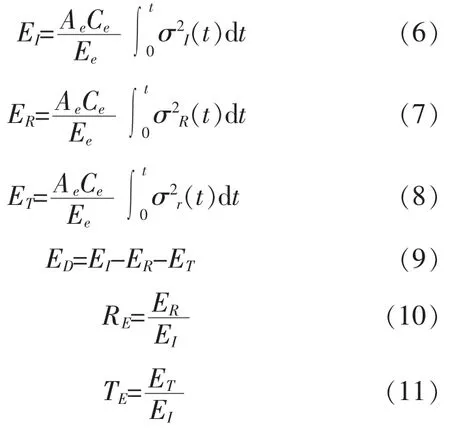
其中，σI（t）、σR（t）、σT（t）分别表示 SHPB 试验中入射、 反射和透射波的应力时程曲线；Ae、Ce、Ee分别为弹性杆的横截面积、纵波速度、杨氏模量。

依据上述公式计算出不同节理厚度下各能量比值的平均值如表5，完整试样的反射与透射能量比35.93%和29.49%。各能量比的变化规律如图10，从整体变化趋势来看，随着节理厚度的增加反射能量比（ER/EI）呈弱幂函数增长，最高为43.68%，涨幅为24.48%；节理试样的透射能量比（ET/EI）随节理厚度的增加， 呈下降趋势， 最低为 21.82%， 降幅为31.10%，与反射能量比的变化趋势相反。 另外通过比较反射和透射能量比值的上升和下降幅度可知，透射能的下降大于反射能的增加，这说明平行节理的存在影响了应力波在试件中的传播，其在动载条件下的变形、破坏影响了能量的传递，导致能量透射系数逐渐减小。由于反射和透射系数会受到波的多次反射与透射影响，因此用反射和透射能量比来表示冲击过程中波的衰减更具有代表性。

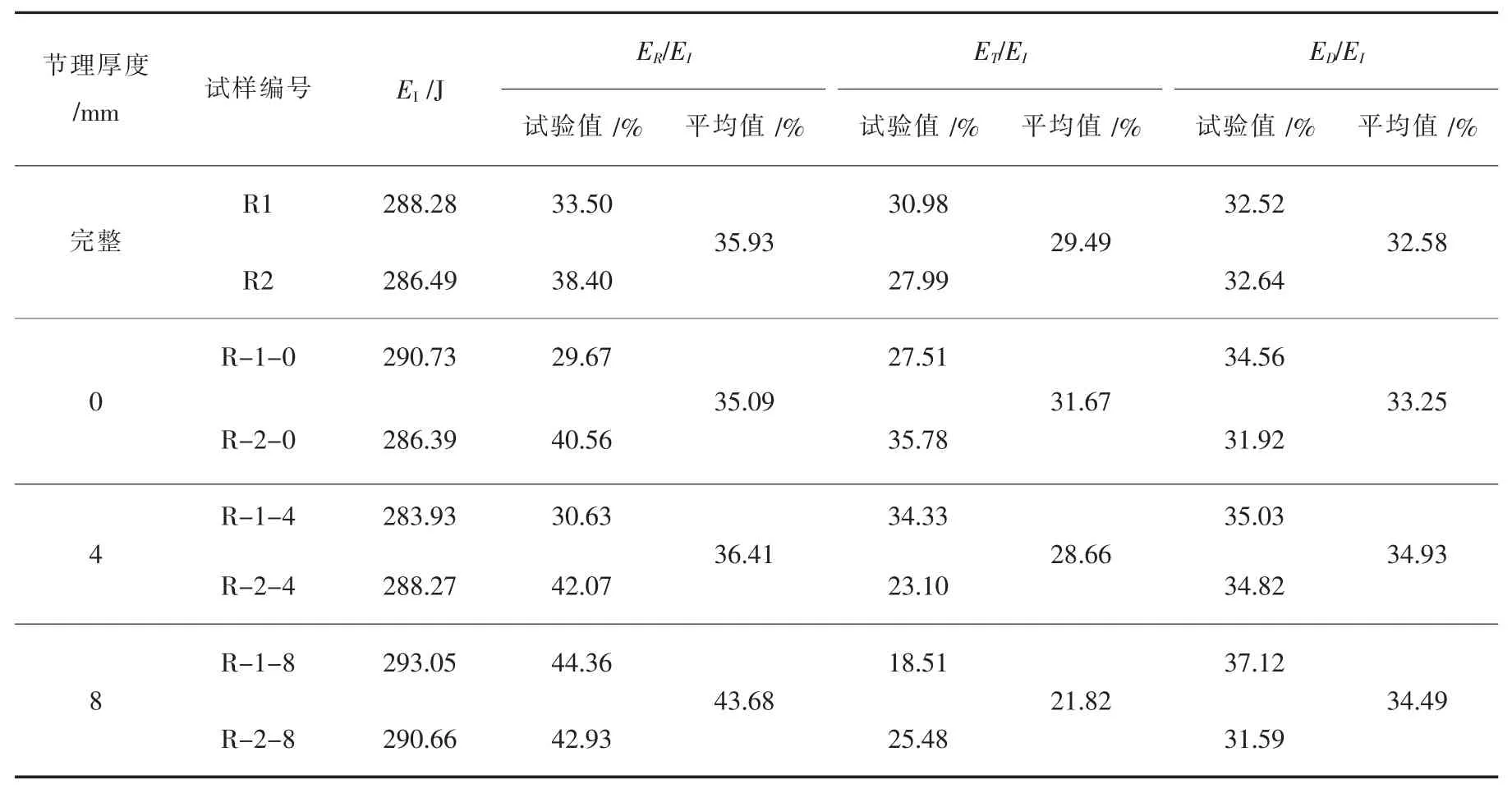
表5 不同节理厚度下各能量比值

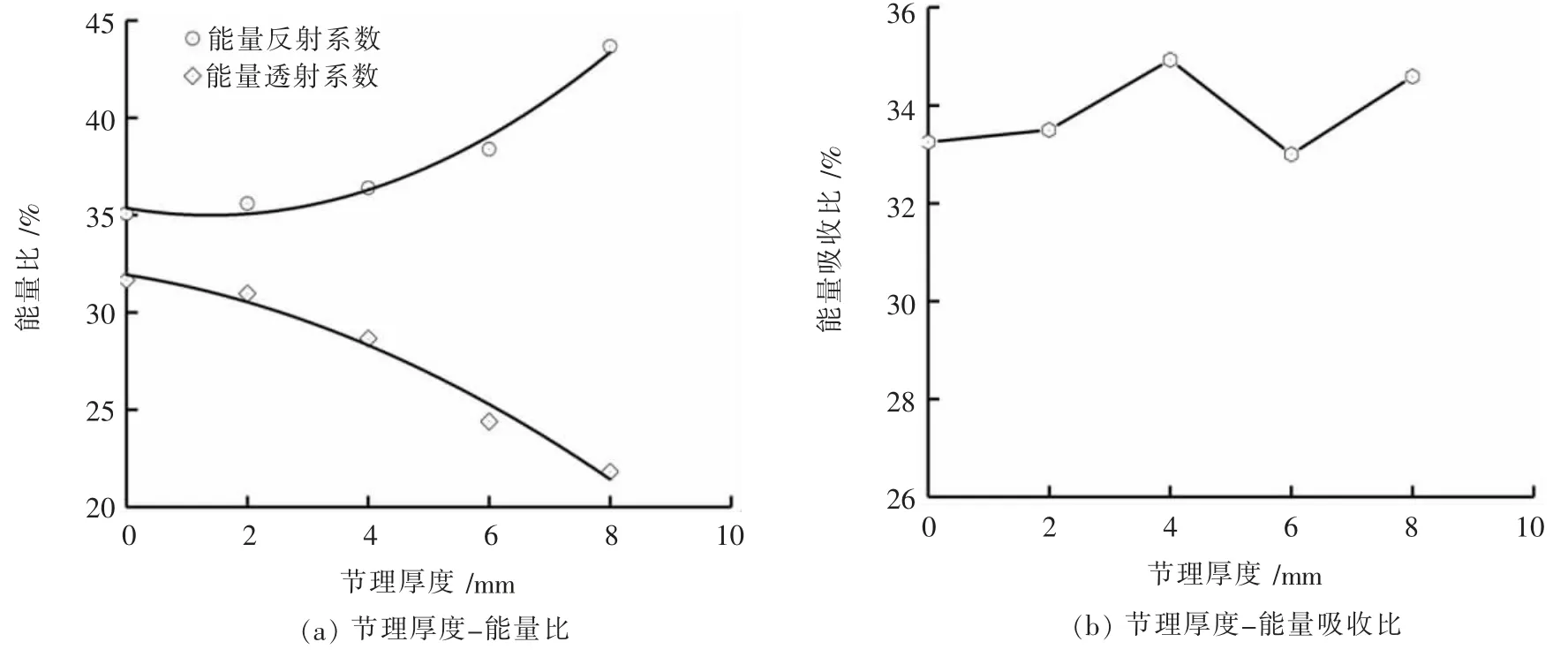
图10 各能量比与节理厚度的关系

岩石工程中岩石的破碎多与破碎过程中吸收的能量有关。 完整试样的能量耗散比为32.58%。图10（b）为能量耗散比随节理厚度的变化趋势，其变化趋势与峰值强度曲线相似，耗散能量变化幅度为 2.06%，2.82%，7.21%，1.29%，6.17%（与完整试样相比）。 由此可见，当节理厚度为6 mm 时，耗散能量比最低， 其值为33.01%， 同时在该厚度条件下，岩石的峰值强度也是最低的。 根据上述分析可知，当岩石中存在这类平行节理时，调整合理的节理厚度可以明显增大爆破过程中岩石的能量吸收率和破碎效果。

3.4 能量表征的损伤变化规律

在冲击载荷条件下， 分析红砂岩试样的损伤变量。 除了动态弹性模量的变化和声波传播速率的变化外， 能量耗散的角度分析也是一种有效的分析方式[29-31]。

其中，wd为冲击过程中红砂岩试样的总耗散能密度；u 为试样破坏总吸收能密度；σ 和 ε 分别为应力和应变。

根据公式（6）～（14）计算出节理试样在冲击过程中的各能量及损伤变量的变化如表6，数据拟合情况如图11 和图12。 由图11 可以明显看出入射能随速度的增大呈线性增加且增幅很明显； 与入射能相比，反射能和透射能虽都有增长趋势，但增幅较小且都呈二次函数变化趋势； 反射能整体上大于透射能，但增长幅度较透射能小，这是由于在该试验速率下冲击时，尽管试样的破碎程度较初始速率大，但试样并没有完全破碎且还有一定的承载能力， 随着入射能的增大， 用于内部裂隙的发育和试样破坏的能量也随之增大，相应的反射能和透射能也增加。

表 4 依据公式（13）、公式（14）计算出了各速率下节理试样的损伤变量，且对数据进行了规律分析和拟合处理（如图12），得出损伤变量随速率的增大呈二次函数增长的关系d=0.0055v2-0.1164v+0.9293，损伤变量表现了试样的破坏程度，其值越大则试样破碎的块度越小，即破坏程度越高[32]。

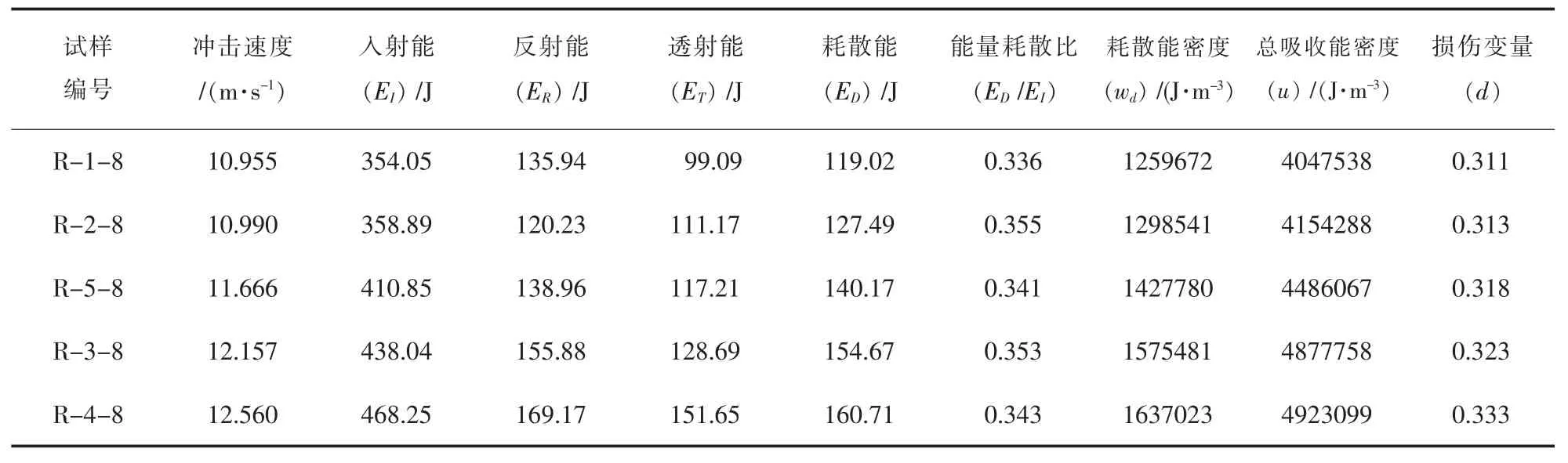
表6 不同冲击速率下节理红砂岩试样各能量及损伤变量的变化情况

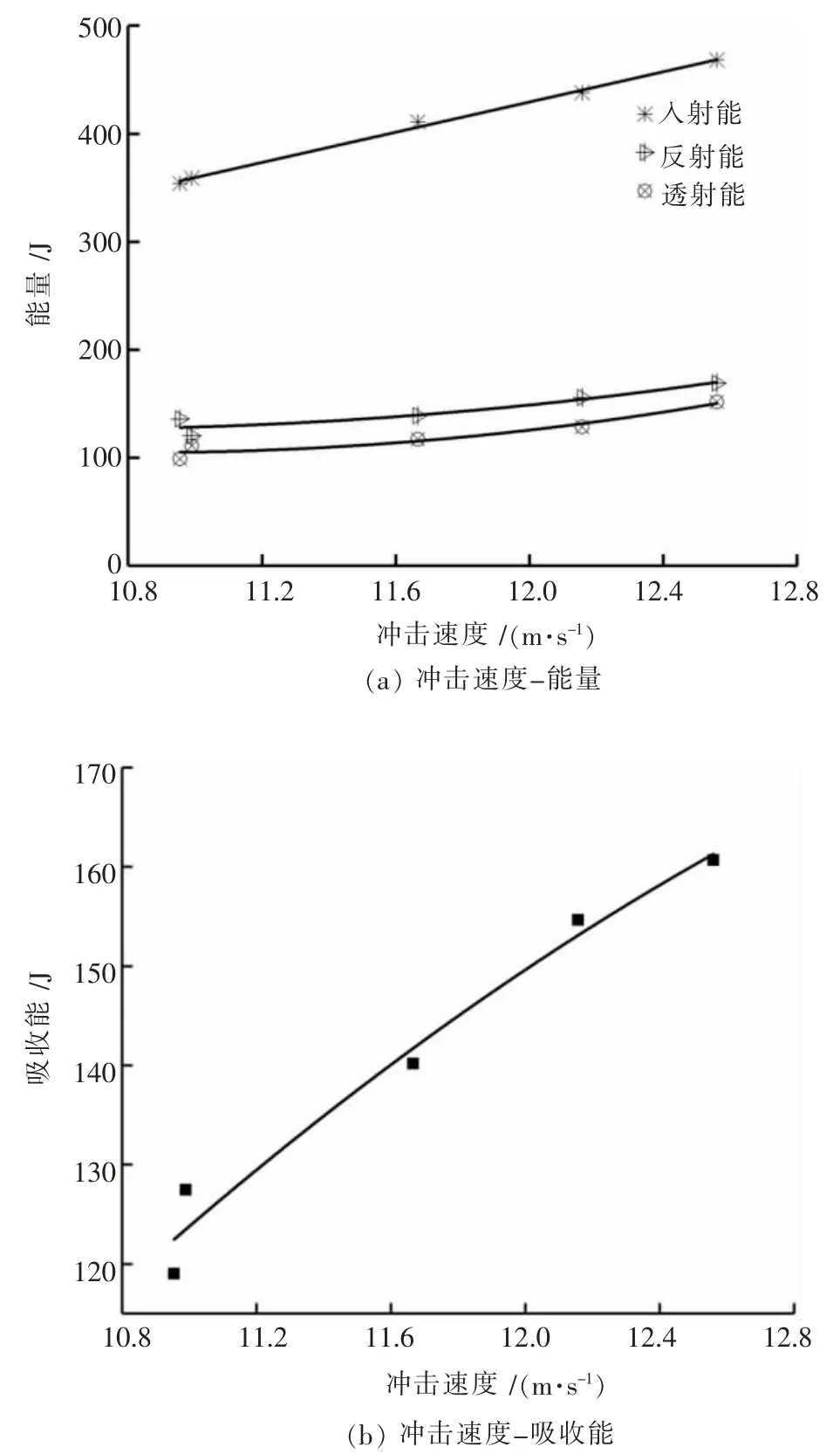
图11 不同冲击速度下的能量变化曲线

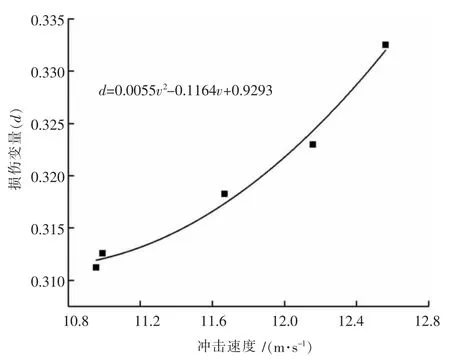
图12 损伤变量与冲击速度的关系

4 结 论

对不同节理厚度下的红砂岩进行冲击试验以研究其对应力波的传播和节理试样破坏模式的影响，得出以下结论：

1）在试验所述冲击条件下，红砂岩中平行节理的存在影响着应力波的传播， 随着节理厚度的增加，反射系数呈线性增大，透射系数呈弱幂函数减小， 在节理厚度为6 mm 时透射系数达到最小值52.28%。

2）在试验所述冲击条件下，节理红砂岩的破坏形态随厚度变化并未表现出明显变化，但靠近入射杆一端的破坏程度随厚度的增加而增大。节理厚度的变化并不会对岩石的动态应力-应变曲线形状产生很大影响，但随着节理厚度的增加，岩石的峰值强度先减小后增大，在节理厚度6 mm 处强度达到最低。

3）在试验所述冲击速率范围内，平行节理岩石的损伤变量随冲击速率的增大呈二次函数规律（d=0.0055v2-0.1164v+0.9293）递增。 冲击速度越大，损伤变量越大，相应的岩石的破碎程度越高。