黏弹性地基上变截面Timoshenko梁稳态谐振动分析
2021-03-23 07:17:32熊海超葛仁余张佳宸卢港伟
安徽工程大学学报 2021年1期
熊海超，葛仁余，张佳宸，夏 雨，卢港伟
(安徽工程大学 建筑工程学院，安徽 芜湖 241000)
振动通常由两部分组成，一是按结构自振频率振动，二是按荷载频率振动。由于在实际振动过程中存在着阻尼力，故按自振频率振动的部分将逐渐消失，只剩下按荷载频率振动的部分。一般两种振动同时存在的阶段为“过渡阶段”，后来只按荷载频率振动的阶段为“平稳阶段”，而实际问题中“平稳阶段”的振动较为重要。
Hasheminejad等基于线弹性理论研究了简支梁在移动荷载作用下的瞬态弹性动力响应的半解析解；Fan等提出了基于复正态模态分析的粘弹性边界支座梁受迫振动的分析方法，分析了粘弹性支座对梁受迫振动响应的影响；Wielentejczyk等研究了简谐荷载作用下粘弹性梁的几何非线性稳态振动问题以及其稳态解的稳定性；Simsek等研究了功能梯度简支梁在集中移动谐波荷载作用下的自由振动和强迫振动，分析了梁的材料分布、移动谐波荷载速度和激励频率对梁动力响应的影响；Khalili等运用瑞利-里兹(Rayleigh-Ritz)法和微分求积(DQM)法研究了功能梯度梁在移动荷载作用下的强迫振动，以及材料特性和运动荷载惯量对动力响应的影响；Yang等运用无网格边界积分方程法研究了功能梯度梁在谐波荷载和瞬态荷载作用下的强迫振动问题；Han等运用格林函数单元法研究了具有阻尼效应的简谐荷载作用下轴向功能梯度非均匀梁稳态动力响应的解析解，分析了解的阻尼效应和对称性质。
在工程实际中，当遇到受弯构件承受谐振荷载的情况，这时一般总是将结构及其构件的设计避开共振区。当避开共振区时，在稳态谐振动过程中即简谐振动进入”平稳阶段”，所有的荷载、变形、内力、支反力和惯性力均按同一简谐规律变化，即同时达到各自的最大值。此时，受弯构件的稳态谐振动的位移和内力幅值可以直接得出，而不必将振型分解，这样的计算偏于安全，并大大简化了问题的求解。Sun采用积分变换法研究了弹性地基梁在简谐线荷载作用下的闭合挠度响应，得到其稳态响应的显示表达式，给出了不同载荷频率和速度组合时的闭合挠度；Luo等研究了弹性支承的Timoshenko梁在简谐线荷载作用下的稳态响应，给出了其相应的闭合解；Kargarnovin等研究了非线性黏弹性地基支承的无限长梁在简谐运动荷载作用下的响应，参数化分析了加载速度和激励频率对梁响应的影响；Seong等研究了弹性地基上受简谐荷载作用的剪力梁柱的振动和屈曲，分析了梁的剪切变形和轴向压缩对稳态响应的影响，给出了预测临界速度、临界频率和轴向屈曲力的表达式。
文章运用微分求积法研究了有限长变截面Timoshenko梁上作用简谐线动荷载的梁横向稳态谐振动响应问题。基于Timoshenko梁理论建立了变截面梁横向稳态谐振动控制方程组，将变截面梁横向稳态谐振动响应的计算转化为一组含有复变系数线性常微分方程组的两点边值问题，运用微分求积法求解，可获得梁横向稳态谐振动的位移与内力幅值，同时可以获得相应梁的时程曲线。针对地基梁复变系数微分方程所得的复数解，能够很好地反映地基阻尼对梁横向稳态振动时梁位移与内力的衰减，且文中方法对梁截面的几何轮廓形状无需任何限制条件，便于工程应用。
1 Timoshenko梁基本理论
黏弹性地基变截面Timoshenko梁的力学模型如图1所示。为研究(黏)弹性地基梁的横向稳态谐振动，建立(黏)弹性地基上一长度为l
的弹性变截面Timoshenko梁模型，其截面面积沿轴向任意连续变化，x
是从梁的左端起点沿轴线方向的坐标。梁横向稳态谐振动时，假设梁仅在x
-w
平面内变形，且梁的截面位移属于小变形范畴，忽略梁轴向变形的影响。设任意x
处截面中性轴上的位移，挠度为w
(x
,t
)，截面转角为φ
(x
,t
)；材料的弹性模量为E
、质量密度为ρ
、剪切模量为G
、泊松比为ν
、梁截面的剪切修正系数为κ
，均为常量；梁截面面积为A
(x
)，截面转动惯量为I
(x
)，均为关于x
的函数，设A
(x
)=A
h
(x
)，I
(x
)=I
h
(x
)，其中h
(x
)、h
(x
)为关于x
的连续可微函数，A
、I
分别对应于左端边界x
=0位置处梁截面面积与截面惯性矩。由图1可知，M
(x
,t
)、V
(x
,t
)、P
分别为x
处梁横截面上的弯矩、竖向力与水平向恒定力，P
>0表示P
为轴向压力，P
<0表示P
为轴向拉力；φ
、γ
、α
分别表示梁微元横截面转角(由纯弯矩引起的中性轴的转角)、由纯剪力引起的中性轴的剪切角、由弯矩和剪力共同作用引起的中性轴的实际转角，均为关于x
、t
的函数；f
(x
,t
)表示由横向振动引起的单位长度梁上的横向惯性力，m
(x
,t
)表示由横向振动引起的单位长度梁上的转动惯性力矩，均为关于x
、t
的函数；q
(x
,t
)=F
(x
)e
为梁承受的谐振线荷载，其中F
(x
)为激振力幅值，ω
为激振荷载频率；kw
、cw
、gw
分别表示黏弹性地基的弹性系数、阻尼系数与剪切系数。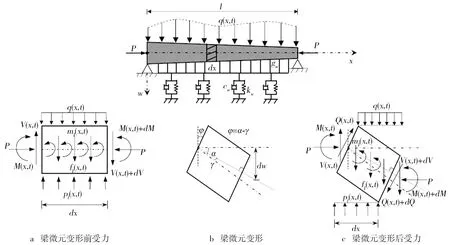
图1 黏弹性地基变截面Timoshenko梁的力学模型
由图1b可知，Timoshenko梁微元段变形存在几何关系：
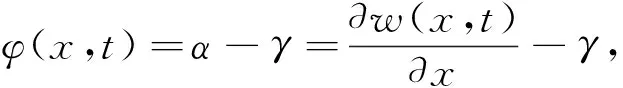
(1)
Q
(x
,t
)为梁在x
位置处横截面上的剪力，梁微元变形后，横截面上的竖向力V
(x
,t
)与剪力Q
(x
,t
)及水平力P
存在以下关系：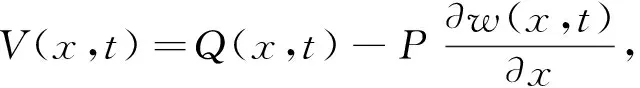
(2)
图1a中，P
(x
,t
)表示三参数Pasternak黏弹性地基对单位长度梁段的地基反力，其方程可表示为：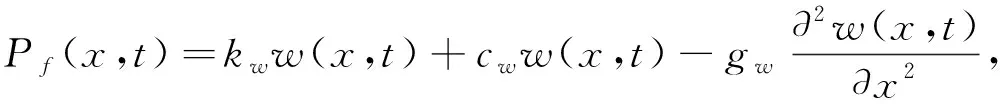
(3)
由图1a、图1b、图1c可知，根据梁微元变形的平衡条件，结合式(1)、式(2)、式(3)得到Timoshenko梁稳态谐振动控制微分方程组如下：
(4)
考虑梁横向稳态谐振动时，所有荷载、变形、内力、支反力和惯性力等均按荷载激励频率振动的规律变化，并同时达到各自的最大值。可设：
w
(x
,t
)=W
(x
)e
,φ
(x
,t
)=Φ
(x
)e
,q
(x
,t
)=Q
e
,(5)
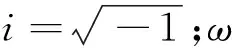
将式(5)代入式(4)，并引入下列无量纲参数，得到梁稳态谐振动控制方程组的无量纲形式如式(6)所示。
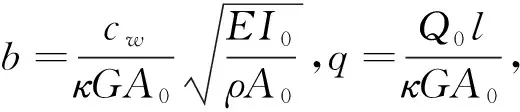
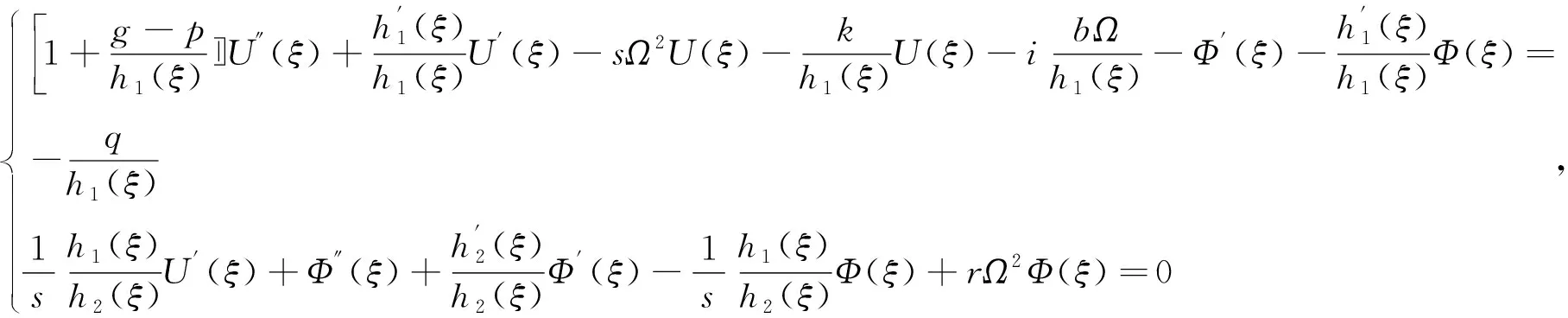
(6)
式中，r
是影响梁横截面转动惯量的无量纲回转半径，当左端截面一定时，其值可反映梁长细比的大小；s
是反映梁剪切变形的无量纲参数；Ω
是外部激励荷载的无量纲角频率。为方便方法的描述，引入下列系数参量代入式(6)，得到式(7)。
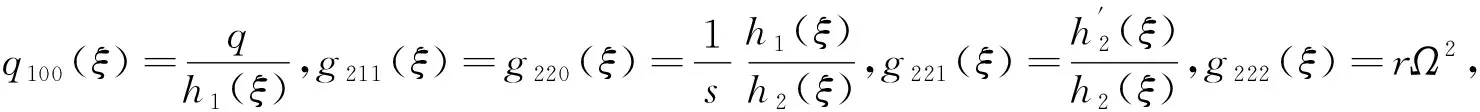
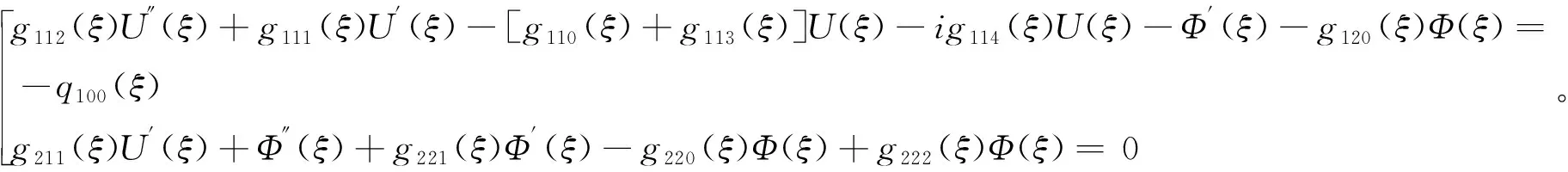
(7)
将区间ξ
∈[0,1]离散为n
段，0=ξ
,ξ
,ξ
,ξ
-1,ξ
=1，共n
+1个节点。采用标记C、H和F分别表示固支、简支和自由三种梁的端部支承形式，如C-H表示梁两端的支承形式为左端固支、右端简支。因此梁稳态谐振动的各类边界条件为：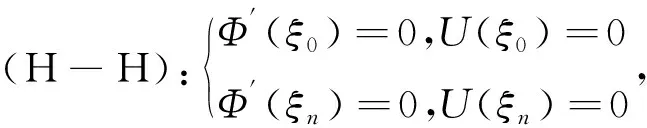
(8a)
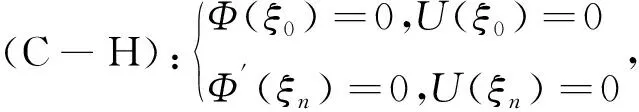
(8b)
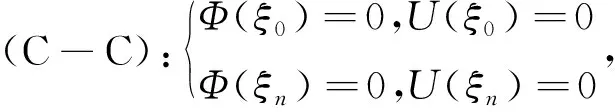
(8c)
(8d)
至此，变截面Timoshenko梁横向稳态谐振动响应问题转化为求解满足相应边界条件式(8)的复变系数常微分方程组式(7)的两点边值问题，文中采用微分求积法。
2 微分求积法基本原理
研究采用非均匀等比数列节点离散模型对区间ξ
∈[0,1]进行节点间距变步长设置，如图2所示，具体节点离散公式为：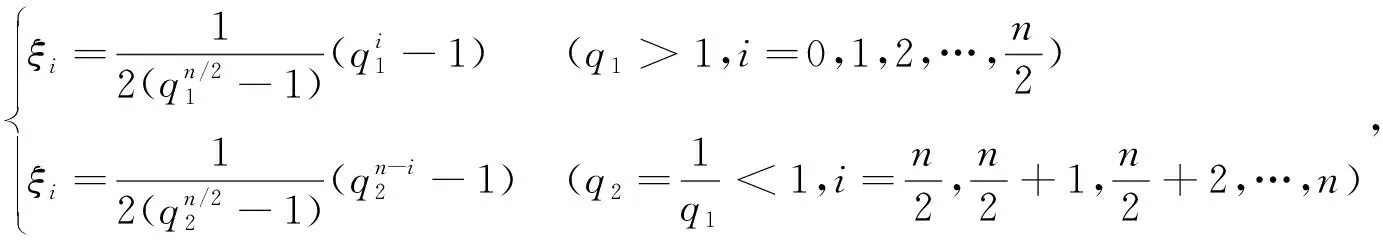
(9)
式中，q
和q
为调整非均匀等比数列节点划分密度的公比，可根据计算精度需要进行调整。这种在梁两端支座附近区域布置较多的细密非均匀节点，无论从数学角度还是力学角度，对于微分求积法的计算精度都非常有利。
图2 变截面梁的节点离散模型
考虑一维函数U
(ξ
)、Ф(ξ
)在区间ξ
∈[0,1]上可微，区间离散为n
段，0=ξ
,ξ
,ξ
,ξ
-1,ξ
=1，共n
+1个节点，即n
+1个节点上函数的导函数值可用n
+1个节点对应函数值的加权线性求和来近似表示。将函数U
(ξ
)、Ф(ξ
)及其相应的导数值用其各节点的函数值进行拉格朗日(Lagrange)插值表示，即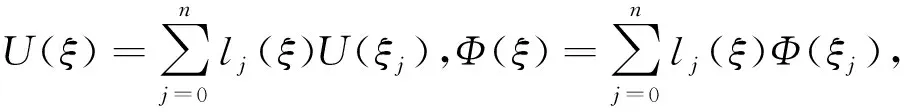
(10)
式中，l
(ξ
)为拉格朗日插值多项式，其具体形式为：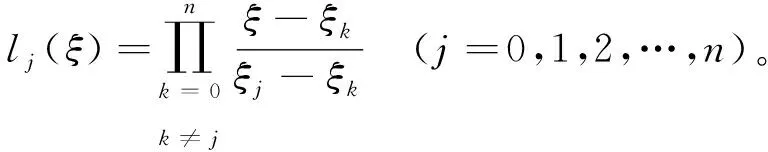
(11)
由式(10)，分别对函数U
(ξ
)、Ф(ξ
)求一阶导数，得到：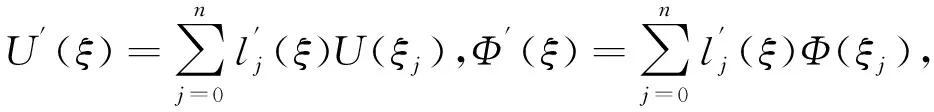
(12)
将式(12)中的ξ
离散化，从而有：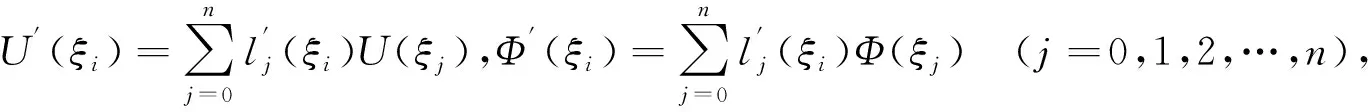
(13)
依此类推，可得：
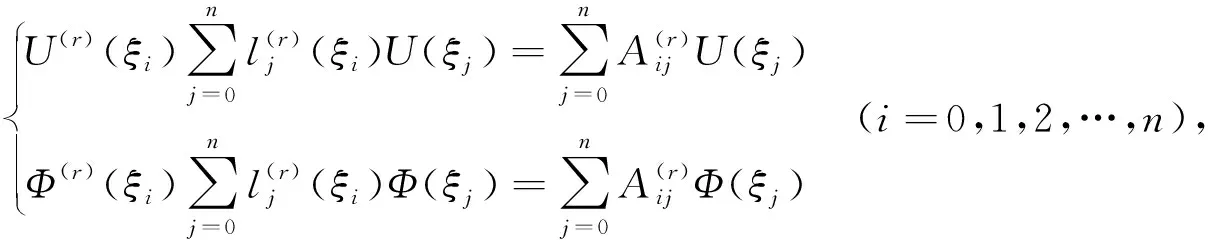
(14)
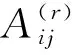
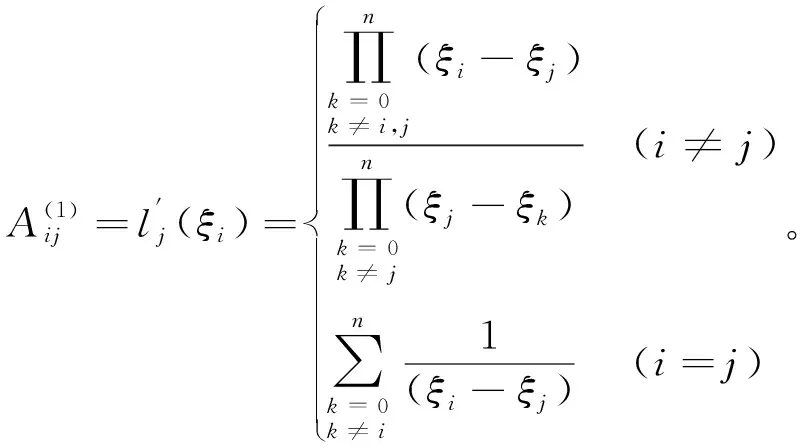
(15)
将式(13)用向量形式表达，得到：
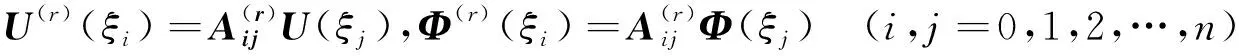
(16)
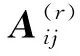
ξ
)={U
()(ξ
),U
()(ξ
),…,U
()(ξ
)},(ξ
)={U
(ξ
),U
(ξ
),…,U
(ξ
)},()(ξ
)={Φ
()(ξ
),Φ
()(ξ
),…,Φ
()(ξ
)},(ξ
)={Φ
(ξ
),Φ
(ξ
),…,Φ
(ξ
)},
由于微分关系
(17)
因此，各阶导数的加权系数矩阵之间的关系为：
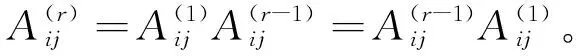
(18)
将式(7)离散，并用向量形式表示，其中微分方程组中的变系数写成对角阵形式，即
=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)},=diag
{g
(ξ
),g
(ξ
),…,g
(ξ
)}。从而得到梁横向稳态谐振动控制方程组的向量矩阵形式：
(19)
根据复系数代数方程组的表达形式，将式(19)分解为：
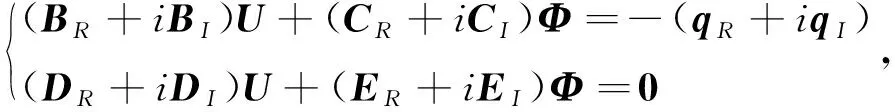
(20)
式中，矩阵、分别表示矩阵的实部与虚部，矩阵、、的实部与虚部均同理表示；向量、分别表示向量的实部与虚部；由此可知，两未知向量解的形式为：=+i
、=+i
。不失一般性，以悬臂梁(C-F)情况为例进行边界条件讨论，则其相应的边界条件的向量形式为：
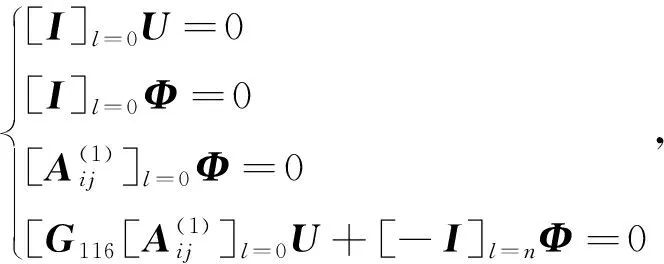
(21)
n
行，获得梁稳态谐振动控制方程的复系数代数方程组的向量矩阵形式。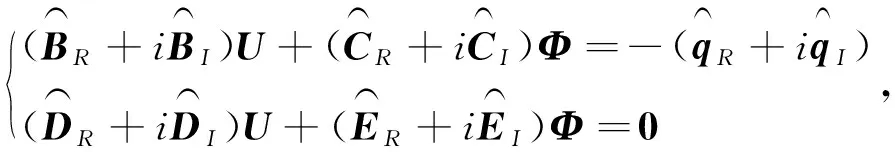
(22)
为便于编程计算，式(22)进一步简化为：
(+i
)=+i
,(23)
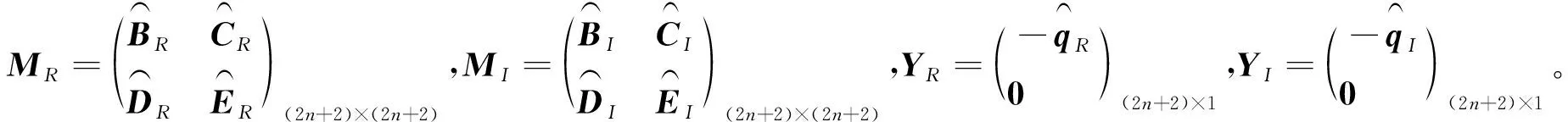
解向量形式为：
n
+2个未知复数向量(,)的复系数线性代数方程组，通过复系数方程组的全选主元高斯(Gauss)消去法可直接求出复数解向量(,)，即为相应梁稳态谐振动离散化后各点的无量纲挠度U
(ξ
)和截面转角Ф(ξ
)的幅值。根据Timoshenko梁理论，结合基本参量单位，可进一步计算获得梁各节点的内力幅值。3 数值算例与讨论
表1 一端固支、一端简支Euler梁稳态谐振动的位移与内力
算例
2黏弹性地基上Timoshenko梁的稳态谐振动响应。考虑黏弹性地基约束的影响，梁段区间划分点数
n
=30，公比q
=1.2时，运用微分求积法求解式(7)和式(8d)，对黏弹性地基上Timoshenko悬臂梁(C-F)横向稳态谐振动响应进行研究，这里取均布荷载幅值Q
=100 kN/m，轴向荷载P
=-40×40 MN，其他具体参数参照文献[17]确定取值范围。算例主要分析了无量纲地基弹性系数k
、无量纲地基剪切系数g
及无量纲地基阻尼系数b
对梁位移和内力幅值的影响。地基弹性系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响如图3所示。由图3可知，无量纲地基弹性系数k
对C-F梁横向稳态谐振动时地基梁位移与内力的影响。由图3a、图3b、图3c、图3d计算结果可知，地基梁的挠度、转角、弯矩和剪力幅值随着无量纲地基弹性系数k
的增大而减小。剪切系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响如图4所示。由图4可知，无量纲地基剪切系数g
对C-F地基梁横向稳态谐振动时梁位移与内力的影响。由图4a、图4b、图4c、图4d计算结果可知，地基梁的挠度、转角、弯矩和剪力幅值随着无量纲地基剪切系数g
的增大而增大。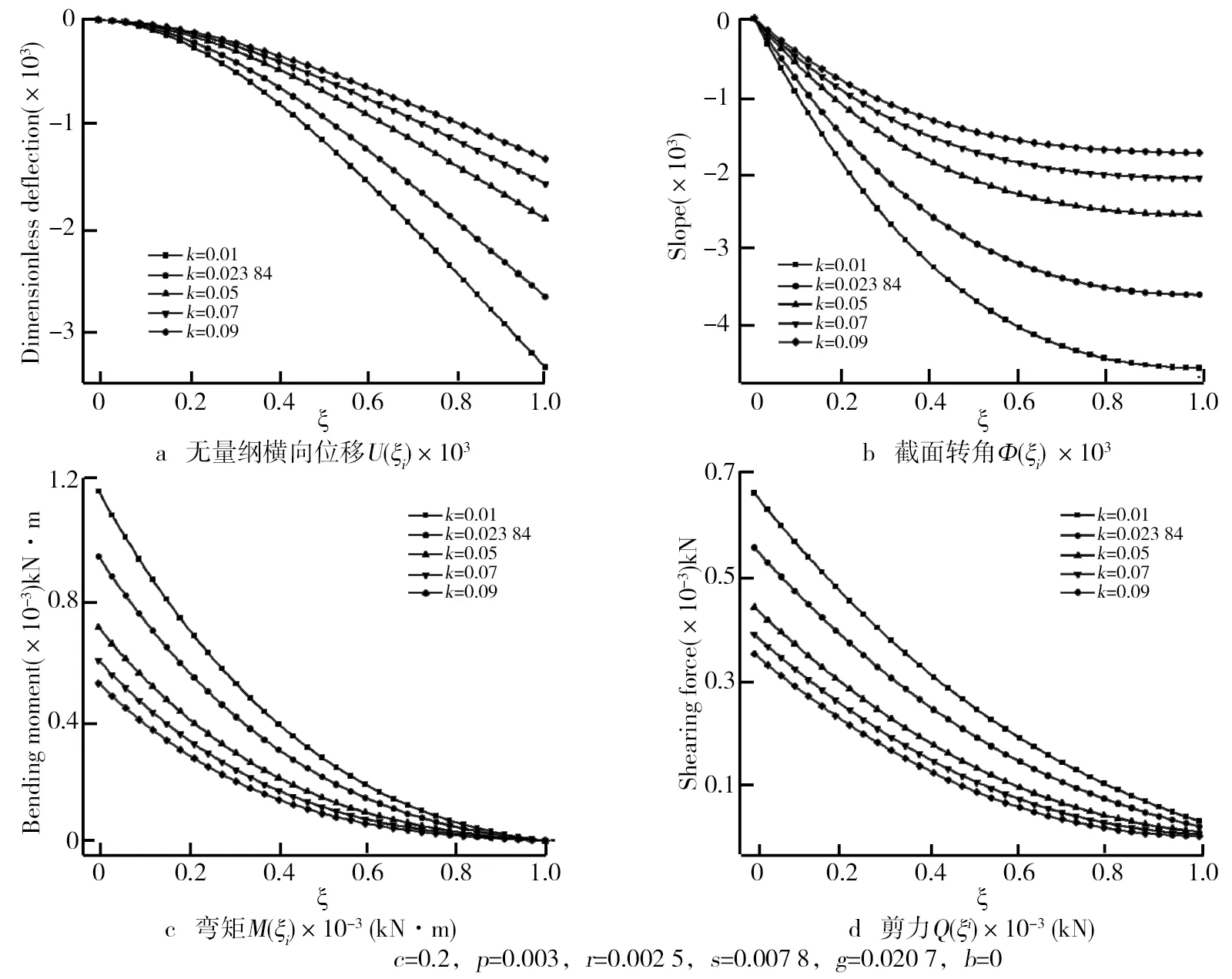
图3 地基弹性系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响
图4 剪切系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响
阻尼系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响如图5所示。由图5可知，无量纲地基阻尼系数b
对C-F地基梁横向稳态谐振动时梁位移与内力的影响。由图5a、图5b、图5c、图5d、图5e、图5f、图5g、图5h计算结果可知，地基梁的挠度、转角、弯矩和剪力幅值实数部分随着无量纲地基阻尼系数b
的增大而减小，挠度、转角、弯矩和剪力幅值的虚数部分随着无量纲地基阻尼系数b
的增大而增大。综上，地基弹性系数k
、剪切系数g
及阻尼系数b
对黏弹性地基上Timoshenko梁位移和内力幅值的影响比较明显，不可忽略。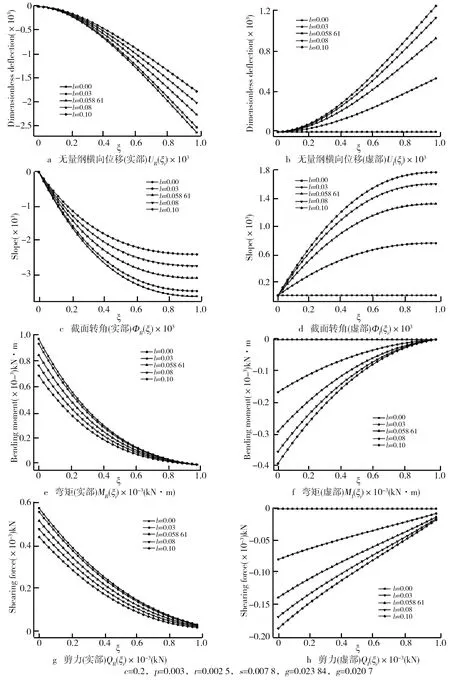
图5 阻尼系数对Timoshenko悬臂梁(C-F)位移和内力幅值的影响
4 结论
研究基于Timoshenko梁理论，将有限长变截面梁横向稳态谐振动响应的计算转化为求解一组含有复变系数常微分方程组的两点边值问题，运用微分求积法求解该复变系数常微分方程组，从而获得梁横向稳态谐振动时的位移与内力。研究主要结论如下：由微分求积法获得的Euler梁稳态谐振动的位移及内力计算值与精确解、已有文献的计算结果吻合，说明了微分求积法分析梁稳态谐振动问题的有效性和精确性。数值计算结果表明，地基弹性系数k
、剪切系数g
及阻尼系数b
对黏弹性地基上Timoshenko梁位移和内力幅值的影响比较明显。具体表现为：梁的位移和内力随地基弹性系数k
的增大而减小、随地基剪切系数g
的增大而增大、随地基阻尼系数b
的增大而减小。研究方法具有通用性和适应性强的特点，可以推广到抗弯刚度和单位长度质量连续变化的功能梯度材料Timoshenko梁的稳态谐振动的研究中，具有一定的工程应用价值。猜你喜欢
现代装饰(2022年6期)2022-12-17 01:07:38
大电机技术(2022年3期)2022-08-06 07:48:24
核科学与工程(2021年4期)2022-01-12 06:30:04
煤气与热力(2021年4期)2021-06-09 06:16:54
中国生殖健康(2020年8期)2021-01-18 03:05:40
艺术品(2020年8期)2020-10-29 02:50:02
中华戏曲(2020年1期)2020-02-12 02:28:18
城市道桥与防洪(2019年5期)2019-06-26 00:55:46
中国生殖健康(2018年3期)2018-11-06 07:20:18
传记文学(2017年9期)2017-09-21 03:16:58
