脉冲射流动力机构的结构设计和数值模拟*
严忠 陈小元 王委 纪照生 史杏杏
(1.中石化华东石油工程公司江苏钻井公司 2.中国石油大学(北京))
0 引 言
我国深层油气资源较为丰富,深部地层具有剩余资源量多、发展潜力大等特点[1-2],但是也存在地层环境复杂和岩石硬度大等问题,亟需高效破岩方法以提高钻井效率,缩短建井周期,进而提高深层油气开采效益[3-4]。脉冲射流钻井技术能够有效利用并优化分布井底水力能量,在井底形成交变流场,提高射流的清岩效率,并通过降低井底瞬时压力改变井底岩石的应力状态实现辅助破岩[5-7]。水力脉冲射流发生机构可为脉冲射流钻井技术提供稳定的脉冲射流。在理论研究的基础上,国内外学者利用机械振荡阻断等方法改变钻井液的过流面积,设计了脉冲喷嘴和水力振荡器等多种脉冲射流发生机构,并将其应用到钻井工具中,从而改变井底流场,提高机械钻速。
在产生机械阻断的方法中,利用动力机构带动盘阀转动,改变盘阀有效过流面积是一种最常见且有效的方式[8-10]。2013年,崔龙连等[9]设计了一种可以调节频率的脉冲射流提速工具。该工具以涡轮作为动力系统,带动带有圆形孔的上盘阀转动,转动过程中上阀块与下阀板的圆形过流孔重合和错开,在下阀板处产生压力的降低和升高;原本连续流动的钻井液变成脉冲射流,脉冲射流的频率可通过上阀块与下阀板的密封配合次数来调节。2017年,邵冬冬等[10]设计了一种新型脉冲射流钻井工具。该工具以一种小型水动力叶轮作为动力机构,下部阀板伸入钻头内部,高速流动的钻井液进入工具内部后对叶轮产生冲击,迫使叶轮旋转,带动位于叶轮下部且通过中心轴相连的孔式阀板旋转,孔式阀板与下方固定阀板交替关闭,进而打开钻井液过流通道,形成脉冲射流。
以动力机构带动盘阀转动为基础的工具有很多种,但针对动力机构脉冲特性控制的研究尚存不足。为此,本文以叶片驱动盘阀式脉冲射流发生机构为研究对象,利用数值模拟方法对动力机构流场进行计算分析,研究不同排量下动力机构的结构参数与转速、压耗的关系。研究结果可为同类工具的脉冲压力和频率等特性控制提供理论指导。
1 动力机构结构
典型叶片驱动盘阀式脉冲射流发生机构主要由动力机构和盘阀机构组成,如图1所示。动力机构为轴流式水动力叶轮,盘阀机构由动盘阀和静盘阀组成。叶轮轴连接叶轮和动盘阀,静盘阀位于动盘阀下部,并通过台阶限位,其中心设有圆形槽孔配合叶轮轴底端,动盘阀和静盘阀均布有相同数量的过流孔眼。其工作原理为:钻井液流经动力机构,推动轴流式水动力叶轮旋转,将钻井液的动能转化为动力机构的机械能。旋转的叶轮通过叶轮轴带动动盘阀转动。在动盘阀旋转过程中,其上的孔眼和静盘阀上的孔眼交替重合或错开,产生过流面积的变化,从而将连续的钻井液流调制为脉冲射流。

1—叶轮;2—叶轮轴;3—动盘阀;4—静盘阀。
使用流线法将叶片设计为圆弧形,可通过如下角度关系进行叶型参数计算。型线安放角βL为:
(1)
(2)
θ=β2-β1
(3)
式中:β1和β2分别为型线出口角和进口角,γ为型线曲率角,θ为型线中心角。
型线弦长L为:
(4)
r=(D+d)/2
(5)
式中:t为叶轮栅距,n为叶栅稠密度,z为叶片数,r为叶轮中径,D为叶轮外径,d为叶轮轮毂直径。
型线高度e为:
(6)
型线的拱度,即最大厚度h为:
(7)
型线的半径R为:
(8)
叶片叶型的基本参数确定后,参考791翼型的厚度变化规律设计叶片的厚度[11]。791翼型是研制水动力叶轮模型ZBM791-1000时,以设计好的型线作为叶片的工作面,参照791翼型的厚度变化规律向叶片的背面进行加厚,完成叶片的整体厚度设计,其中δmax即为叶片的拱度h。翼型的厚度变化规律如图2所示。
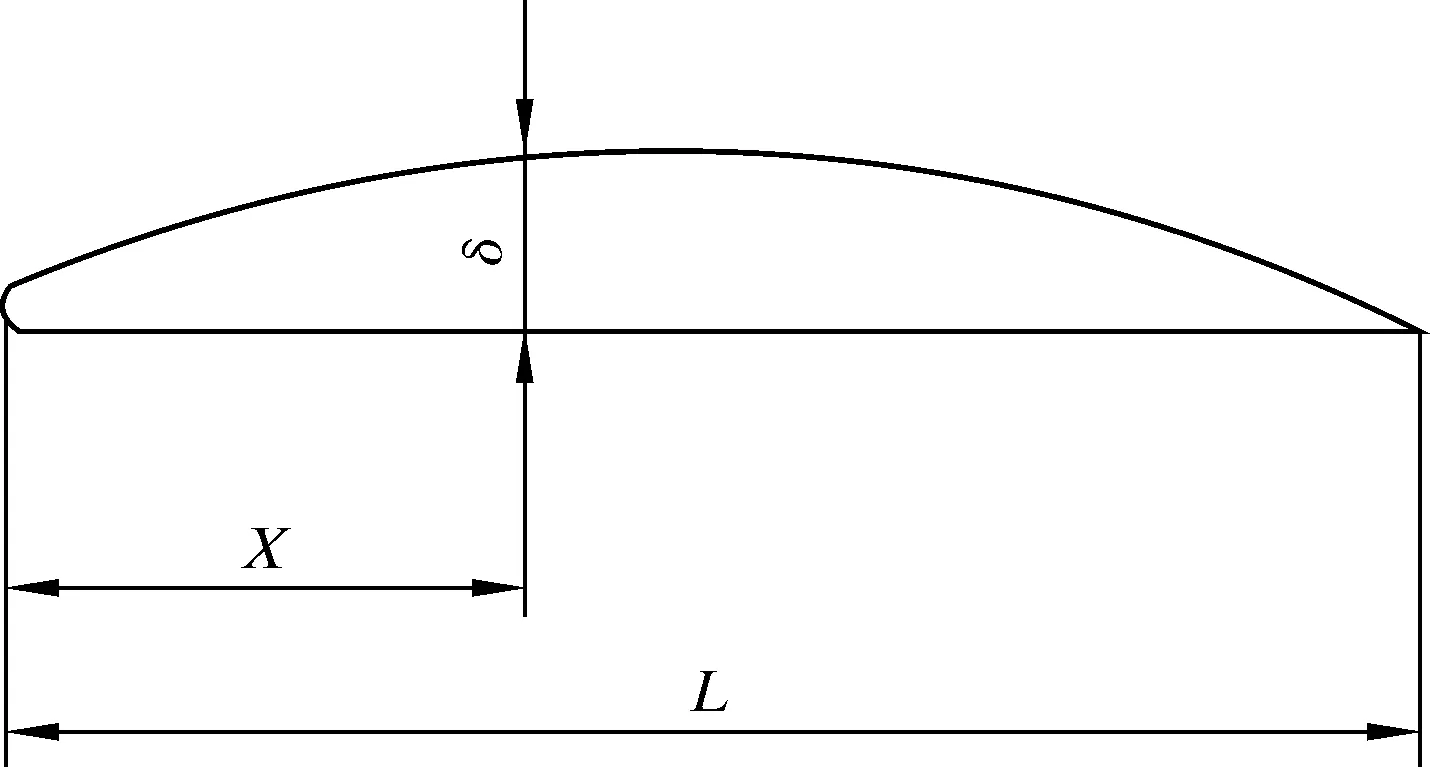
图2 791翼型的厚度变化规律Fig.2 The thickness variation of 791 airfoil
2 模型建立
2.1 几何模型建立

表1 动力机构结构参数Table 1 Structure parameters of the power mechanism
2.2 流域模型建立
在Solidworks中建立动力机构流域三维模型,考虑到动力机构的径向边缘与工具外壳的内壁留有一定空隙,建立直径122 mm的圆柱形流域模型。通过布尔运算从中删减掉动力机构三维模型实体部分,即可得到旋转区域的流域三维模型。分别在其上部和下部设置等外径的进口段和出口段圆柱形流域,该模型即为数值计算所需的井底流域三维模型,如图3所示。

图3 井底流域三维模型Fig.3 Three-dimensional model of the bottom hole flow area
2.3 网格划分
将Solidworks软件中建立的动力机构流域模型直接导入到PumpLinx软件中。设置最大网格单元尺寸为10 mm,最小为1 mm,进行笛卡尔网格划分并自动加密。在非转动区域与叶轮转动区域之间建立交界面,实现数据传递,如图4和图5所示。
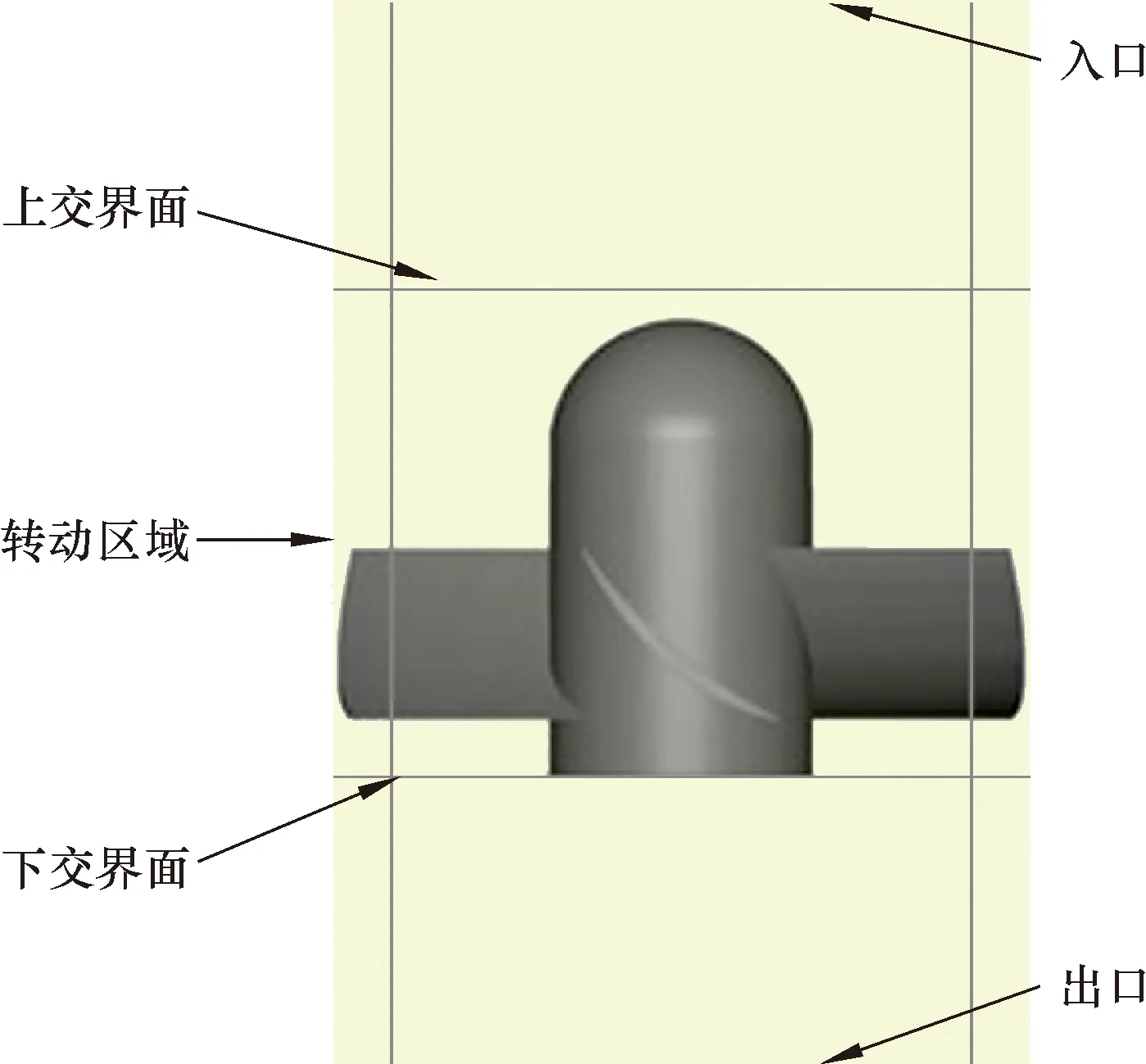
图4 PumpLinx软件内叶轮模型图Fig.4 Impeller model in PumpLinx software
2.4 计算模型建立
利用PumpLinx软件对动力机构实际转动过程进行非定常数值求解。
2.4.1 基本假设
(1)采用具有一定黏度的清水模拟钻井液;
(2)假设流体在井底流场已完全发展为湍流;
(3)假设井底流场内流体为稳态流动,且为各向同性;
(4)假设井底流场内的流体为连续、不可压缩牛顿流体。
2.4.2 计算模型选择
利用计算流体力学方法对钻井液经过动力机构产生的流场进行全工况数值模拟,所用到的控制方程包含质量、动量以及能量方程。动力机构速度、压力场特性分析均可选取单相流体计算模型,但需考虑到流体的流量和黏度,因此选择适用于旋转剪切流的Relizablek-ε计算模型。模型的计算过程中主要用到了k输运方程和ε输运方程。
k输运方程为:

(9)
式中:k为湍动能,J/kg;ε为湍动耗散率,m2/s3;μ为黏度,Pa·s;t为时间,s;ρ为流体密度,kg/m3;ui为速度在i方向上的分量,m/s;μt为湍动黏度,Pa·s;Gk为由于平均速度梯度引起的湍动能的产生项;σk为湍动能k对应的Prandtl数;Gb为由于浮力产生的湍动能k的产生项;YM为可压湍流中脉动扩张的贡献;Sk为源项。
ε输运方程为:
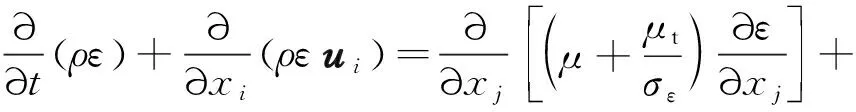
(10)
(11)
η=Sk/ε
(12)
(13)
式中:σε为耗散率ε对应的Prandtl数;v为流体速度,m/s;C1、C2、C1ε、C3k为系数,无量纲;Sε为源项。
2.4.3 计算模块选择
在PumpLinx中添加轴流、湍流和转动3个模块,并进行边界条件设置。轴流模块默认使用PumpLinx内置的轴流泵动网格计算模板,对动力机构进行瞬态变转速求解。根据叶轮结构参数,设定叶片个数、旋转中心坐标和旋转轴坐标,转速变化由软件根据叶轮转速控制方程计算得出[9]:
(14)
式中:I为转动惯量,kg·m2;Mh为水力扭矩;Md为阻力扭矩;Ms为弹簧扭矩;Ma为额外扭矩;Mf为摩擦扭矩,扭矩单位均为N·m。
2.4.4 边界条件设置
设置流体域的类型与黏度,流体介质为清水。
入口和出口边界条件设置:在入口处依据设定的排量和流域模型的过流面积确定流体的初始入口速度;在出口处根据实际工况下的井底压力设置压力边界条件。
旋转区域边界条件设置:选择PumpLinx内置的rotor模型,根据在轴流模块和转动模块设置的参数自动填充旋转体的转动中心和转动轴坐标,设定旋转壁面为动态边界(DynamicBC),由此叶片表面所受到的水压力会转化为水力扭矩Mh,自动添加到软件内置的叶轮转速控制方程中进行计算。
2.5 计算结果处理
PumpLinx软件具备求解器和前、后处理器,提供数据自动采集功能。计算过程中可实时监测动力机构流场的速度与压力分布,并可以绘制转速等特性参数的变化趋势线,提高数据分析的效率。
3 特性分析与参数分析
3.1 动力机构速度场特性分析
图6显示了叶片个数分别为3、4、5、6时叶轮流域内的流速径向分布云图。在两叶片的中间区域流速具有最大值,如6a和图6b所示。靠近叶片工作面上半部分处的流速变小甚至接近0,如图6c和图6d所示,钻井液以一定的流速冲击叶片工作面的下半部分。
图7显示了不同叶轮结构参数下流道区域的流线分布图。经加速后的部分钻井液对叶片背面产生冲击,一定程度上阻挡了叶轮转动,从而降低了叶轮的能量利用效率。通过对比,当叶片个数较多、叶轮内径较大、安放角较大时,流线发展较为流畅,能量损失较少。
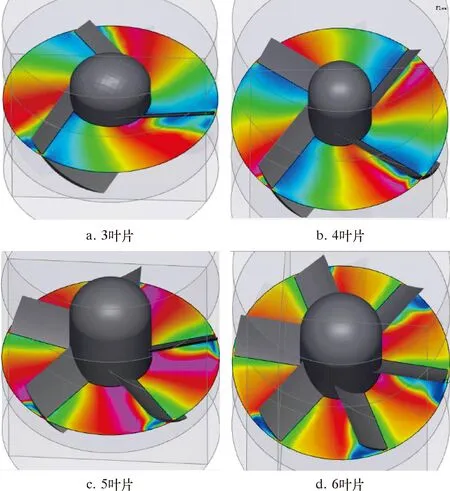
图6 不同叶片个数的叶轮流域内流速分布云图Fig.6 Velocity distribution in the impeller flow area with different numbers of blades
图8a为钻井液最大流速随排量的变化曲线。由图8a可以看出,最大流速随着排量q的增加而增加,排量从15 L/s升高至40 L/s,最大流速由8 m/s增加至13 m/s,增幅百分比为72.39%。图8b表示叶轮内径为46 mm,叶片个数为4时,不同排量下钻井液最大流速随安放角的变化曲线。由图8b可看出:随着安放角的增大,最大流速呈先快后慢的减小趋势,最终趋于平稳;不同排量下安放角由30°增加至63°时,最大流速的减小幅度平均值为2.32 m/s。由此可以看出,由于叶片的倾斜和叶轮的转动,钻井液进入叶片流道后的流速上限得到了提高。安放角为30°,排量为40 L/s时,最大流速可达到15.12 m/s。图8c表示叶片个数为4、安放角为41°时,不同排量下钻井液最大流速随叶轮内径的变化曲线。由图8c可看出:随着叶轮内径的增大,最大流速呈近似线性增加,且增长趋势相同;叶轮内径的增大导致过流面积减小,相同排量下流速增大;叶轮内径由36 mm增加至66 mm,不同排量下最大流速增幅平均值为3.01 m/s,增幅百分比为33.86%。图8d表示叶轮内径为46 mm、安放角为41°时,不同排量下钻井液最大流速随叶片个数的变化曲线。由图8d可看出:随着叶片个数的增加,最大流速增加,叶片个数增多在一定程度上会减小过流面积,但由于叶片整体的厚度(排挤系数)较小,其对过流面积影响较小,叶片个数由3增加至6,不同排量下的最大流速增幅平均值仅为1.64 m/s,增幅百分比为17.09%。

图7 不同叶轮结构参数下流道区域的流线分布图Fig.7 Streamline distribution in the flow area under different impeller structure parameters
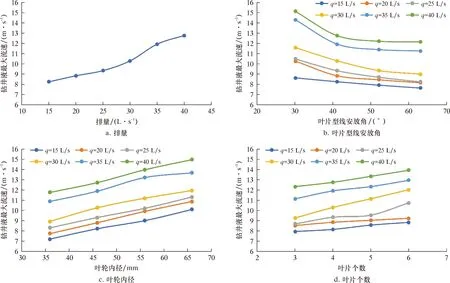
图8 钻井液最大流速随排量、叶片型线安放角、叶轮内径和叶片个数的变化曲线Fig.8 Variation of the maximum flow rate of drilling fluid with the displacement,the blade profile installation angle,the impeller inner diameter and the number of blades
通过对速度场的分析可知:当叶片个数较多、叶轮内径较大、安放角较大时,流线发展较为流畅,能量损失较少;当排量较大、叶片个数较多、叶轮内径较大、安放角较小时,钻井液经过叶片流道时的最大流速较大,从而对叶片工作面的下半部分产生更大的冲击作用。
3.2 动力机构压力场特性分析
对比叶片表面受力情况,分析不同结构参数叶轮的流道内压力分布情况,如图9所示。从图9a可知,随着安放角减小,叶片受力更加均匀。从图9b和9c可知,当安放角一定时,叶片个数与叶轮内径的大小对工作面的受力情况影响不大。因此较小的安放角增大了高流速钻井液对工作面上半部分的直接冲击面积和冲击作用,当安放角较小时,钻井液经过叶片流道时的最大流速也较大,从而对工作面下半部分也会产生相对较大的冲击作用。
图10a表示叶片个数为4、叶轮内径为46 mm、安放角为41°时,叶片工作面所受最大压力随排量的变化曲线。由图10a可以看出,叶片工作面最大受压随排量的增加而增大,在模拟条件下,最大压力在30.006 2~30.041 2 MPa之间变化。图10b表示叶轮内径为46 mm、叶片个数为4时,不同排量下叶片工作面所受钻井液最大压力随安放角的变化曲线。由图10b可以看出,随着安放角的增加,最大压力减小,不同排量下安放角由30°增加至63°时,最大压力的减小幅度平均值为0.015 9 MPa。因此,安放角越小,叶片工作面所受最大压力越高。图10c表示叶片个数为4、安放角为41°时,不同排量下叶片工作面所受钻井液最大压力随叶轮内径的变化曲线。由图10c可以看出,随着叶轮内径的增加,最大压力呈相近的增大趋势,不同排量下叶轮内径由36 mm增加至66 mm时,最大压力增幅平均值为0.019 7 MPa。因此,叶轮内径增大,减小了过流面积,增大了钻井液流速,进而增大了叶片工作面所受最大压力。图10d表示叶轮内径为46 mm、安放角为41°时,不同排量下叶片工作面所受钻井液最大压力随叶轮叶片个数的变化曲线。由图10d可以看出,最大压力基本不随叶片个数的变化而发生变化。
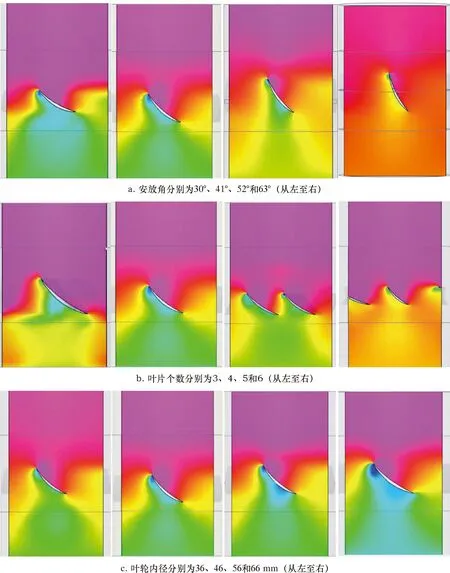
图9 不同结构参数叶轮的流道压力分布图Fig.9 Flow channel pressure distribution under different impeller structural parameters
通过对压力场进行分析,钻井液排量越大、叶轮内径越大、安放角越小时,叶片工作面所受来自钻井液的最大压力越大。
3.3 动力机构转速分析
图11为叶轮转速随钻井液排量、叶轮内径、叶片个数和安放角的变化曲线。在模拟条件下,叶轮转速在200~1 400 r/min之间变化。
由图11a 可知,当叶轮内径为46 mm、叶片个数为4、安放角为41°时,在排量15~40 L/s范围内,叶轮转速随排量的增大而呈线性增大,由666 r/min增加至1 118 r/min,转速增幅为67.87%。排量越大,相同时间内越多的动能转化为叶轮的机械能。
由图11b可知,叶轮转速随叶轮内径的增大先减小后增大。由于内径增大和叶片拱度增大使自身负载的阻力扭矩增大,所以存在最小转速。叶轮内径为56 mm时叶轮转速最低,排量为15 L/s时叶轮转速最低为546 r/min。
由图11c可知:叶轮转速随叶片个数的增加而增大,叶片个数增多,工作面总面积略有增大;由于拱度减小,叶片厚度(排挤系数)减小,叶片个数的增加对过流面积影响较小,过流面积略有减小导致钻井液流速略有增大,因此,叶片个数的增加导致转速增大,但对转速的影响较小,叶片个数由3增加至6时,不同排量下转速平均增幅仅为59 r/min。
由图11d可知:叶轮转速随着安放角的增大而减小,排量较大时近似呈线性减小,排量较小时,转速减小的速度越来越快;安放角越小,相同条件下作用于叶轮的水力扭矩越大,转速越高。

图10 叶片工作面最大受压随排量、叶片型线安放角、叶轮内径和叶片个数的变化曲线Fig.10 The variation of the maximum pressure on the blade working surface with the displacement,the blade profile installation angle,the impeller inner diameter and the number of blades
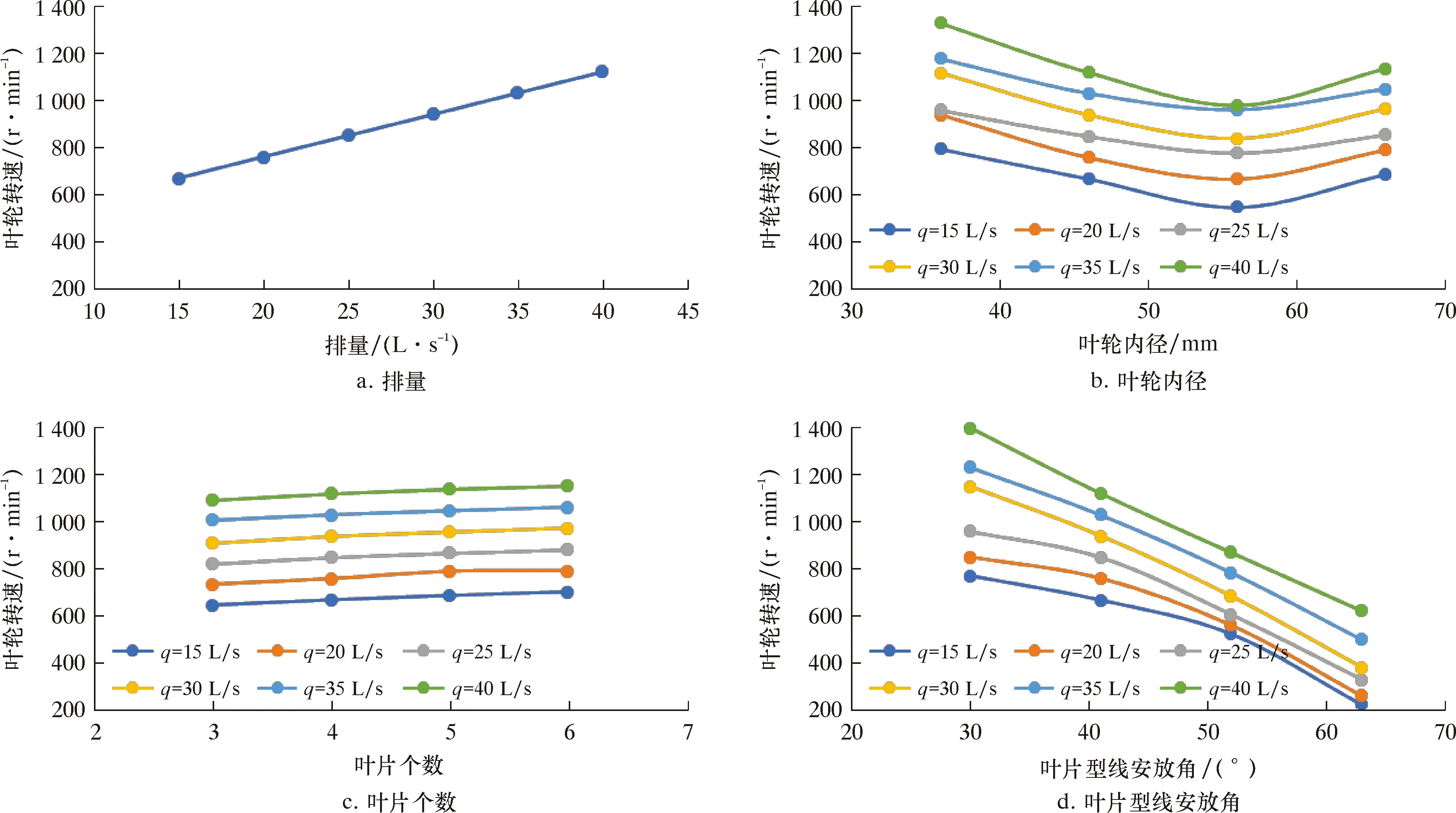
图11 叶轮转速随排量、叶轮内径、叶片个数和叶片型线安放角的变化曲线Fig.11 The variation of impeller RPM with the displacement,the impeller inner diameter,the number of blades and the blade profile installation angle
3.4 动力机构压耗分析
在叶轮的进口和出口流域处设立两个压力监测面,读取监测面的平均压力,计算钻井液流经叶轮的压力损耗。图12为压耗随排量、叶轮内径、叶片个数和安放角的变化曲线。在模拟条件下,叶轮压耗在0.00~0.07 MPa之间变化。
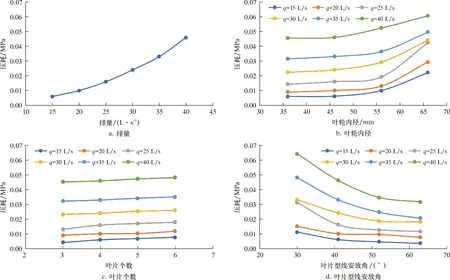
图12 压耗随排量、叶轮内径、叶片个数和叶片型线安放角的变化曲线Fig.12 The variation of pressure loss with the displacement,the impeller inner diameter,the number of blades and the blade profile installation angle
由图12a可知:当叶轮内径为46 mm、叶片个数为4、安放角为41°时,在排量15~40 L/s范围内压耗随排量的增大而增大,增速先慢后快;排量从15 L/s增加到40 L/s,压耗由0.006 MPa增加至0.046 MPa,压耗增幅为667%。
由图12b可知,不同排量下,压耗随叶轮内径的增大而增大,增长速度先慢后快。叶轮内径的增大导致叶轮中径增大,过流面积减小,同排量下钻井液流速加快,更多的钻井液动能转化为叶轮的机械能,压耗增大。
由图12c可知,不同排量下,随叶片个数增加,压耗增大,但变化幅度较小。由于叶片具有一定厚度,随叶片个数增加,减小了过流面积,导致流速和压耗增大,但由于叶片厚度对过流面积影响很小,所以叶片个数对压耗的影响也较小。
由图12d可知,不同排量下,压耗随着安放角的增大而减小,减小速度先快后慢。安放角越小,表明叶片出口角越小,钻井液最终的周向速度就越大,根据动量守恒定理,压耗越大。
4 结 论
(1)不同排量和叶轮结构参数下,叶轮转速在200~1 400 r/min之间变化;叶轮内径为46 mm、叶片个数为4、安放角为41°时,排量由15 L/s增加至40 L/s,转速则由666 r/min线性增加至1 118 r/min。内径与安放角对转速影响较为明显,转速随内径增大而先减小后增大,内径为56 mm、排量为15 L/s时,转速最低达到546 r/min;转速随叶片个数增加而增大,叶片个数由3增加至6时,转速在600~1 200 r/min之间变化,不同排量下平均增幅仅为59 r/min;随安放角增大而减小,不同排量下平均减幅为673 r/min。
(2)叶片个数对转速的影响范围更广,当内径为66 mm、扭矩为0.5 N·m时,转速最大为1 098 r/min;当内径为36 mm、扭矩为5 N·m时,转速最小为90 r/min;当叶轮个数为6、扭矩为0.5 N·m时,转速最大为1 303 r/min;当叶片个数为3、扭矩为5 N·m时,转速最小为118 r/min;当安放角为30°、扭矩为0.5 N·m时,转速最大为1 112 r/min;当安放角为63°、扭矩为5 N·m时,转速最小为122 r/min。
(3)不同排量和叶轮结构参数下,叶轮压耗在0.00~0.07 MPa之间变化;当叶轮内径为46 mm、叶片个数为4、安放角为41°时,随排量由15 L/s增加到40 L/s,压耗由0.006 MPa增加至0.046 MPa;压耗随内径增大而增大,增速先慢后快;压耗随叶片个数增加而增大,随安放角的增大而减小。

