轮毂轴承单元过盈量理论设计及试验研究

熊 伟，葛志华，庞 乔，李曼迪，王 友

（1.湖北文理学院机械工程学院，湖北襄阳441053；2.湖北新火炬科技有限公司，湖北襄阳441004）

汽车轮毂轴承是我国先进制造领域的关键机械基础件，其作用是承载和为轮毂传动提供精确引导，对汽车的安全性、舒适性和经济性有重要影响［1-2］。近20年来，随着对汽车轮毂轴承集成化、轻量化和可靠性的要求不断提升，摆辗铆合技术开始逐步应用于第3代汽车轮毂轴承的制造［3-6］。采用摆辗铆合工艺可将轮毂轴承的内、外法兰铆接成一体，具有预紧稳定、集成度高和可靠性高的优点，同时还可使轮毂轴承整体结构更为紧凑，有利于减少汽车行驶过程中的能量消耗［7-8］，因此该工艺近年来备受国内外汽车零部件厂商的关注。目前在世界范围内，日本、德国和美国等发达国家牢牢占据着中高端轮毂轴承市场并封锁着轮毂轴承制造的关键技术。在我国，虽已逐步采用进口的加工及检测设备，但在轮毂轴承的可靠性设计、核心加工工艺及生产质量管控等软技术实力方面仍与国外发达国家存在较大差距，从而导致国内厂商生产的轮毂轴承多用于中低端车型。因此，有必要持续、系统与深入地开展轮毂轴承单元轴端铆接装配关键技术及其专用加工、检测设备研究。

目前，轴承过盈配合理论及其技术均较为成熟［9-13］。在第3 代轮毂轴承单元的设计制造过程中，常使用过盈配合连接其内圈与内法兰轴。若过盈量太小，则轮毂轴承单元工作时会出现内圈转动现象；若过盈量过大，则会出现内圈破裂现象。因此，过盈量的合理设计是制造轮毂轴承单元的关键。另外，与前两代轮毂轴承单元不同的是［14］，第3代轮毂轴承单元通过轴端摆辗铆接工艺来施加轴向预紧作用。生产实践表明，若采用传统过盈量设计方法，则会忽略铆接工艺的影响，易导致轮毂轴承单元的内圈破裂。

对于轮毂轴承单元制造中的关键共性技术，笔者已对第3代轮毂轴承单元的摆辗铆接工艺、关键技术参数检测方法与检测设备等进行了研究［15-18］。在前期研究的基础上，笔者拟开展轮毂轴承单元过盈量理论设计及试验研究。首先，采用理论公式初步确定轮毂轴承单元内圈与内法兰轴配合的过盈量；然后，采用有限元方法获取轮毂轴承单元过盈配合面的压力分布及其轴向预紧力，并对理论过盈量进行修正；最后，开展相关力学与耐久试验，以验证过盈量理论设计方法的合理性和可靠性。

1 轮毂轴承单元过盈量理论设计

1.1 基础参数计算

在过盈装配后，轮毂轴承单元内圈仅受到过盈配合面的压力，如图1所示。为衡量过盈配合产生的平均应力，用当量直径代替内圈实际直径（对内法兰轴内径亦作同样处理）。内圈的当量直径可用等面积法求得，其计算式为：

式中：De为内圈的当量直径；Df为过盈配合面直径；hi为内圈高度；Ai为内圈截面积。

图1 过盈装配后轮毂轴承单元内圈的受力示意图Fig.1 Schematic diagram of force on the inner ring of hub bearing unit after interference assembly

以2个厚壁圆环过盈配合为基础，采用平面应力假设对轮毂轴承单元过盈配合面的应力及变形进行分析。假设内圈与内法兰轴的弹性模量、泊松比均相同。基于弹性变形理论，可得过盈配合面的压力pf、切向应力σt及静摩擦力ff分别为［19］：

式中：Km为结构参数；Di为内法兰轴的当量直径；E为弹性模量；Δf为过盈配合面的初始过盈量；μf为过盈配合面的静摩擦系数；Af为过盈配合面的面积。

1.2 理论过盈量设计

1.2.1 最小过盈量

为防止轮毂轴承单元的内圈与内法兰轴在工作过程中相对转动，要求其过盈配合面的静摩擦力至少能够抵抗外力的作用。由于过盈量与轮毂轴承单元所受的径向载荷Fr有关，则其内圈与内法兰轴配合的最小过盈量f0min为［19］：

式中：d0为轮毂轴承单元内径；B 为轮毂轴承单元过盈配合面的有效宽度；C0r为轮毂轴承单元所受的径向额定静载荷。

对于乘用车的轮毂轴承单元，要求其在极限载荷（一般为0.6g加速度载荷）下的过盈装配仍不失效。在0.6g 加速度载荷下，轮毂轴承单元所受的径向载荷Fr＞0.2C0r，故可按式（6）确定其内圈与内法兰轴配合的最小过盈量。

1.2.2 最大过盈量

基于配合的包容面与被包容面均不产生塑性变形的原则，可确定轮毂轴承单元内圈与内法兰轴配合的最大过盈量。鉴于内圈加工常采用GCr15整体淬火工艺，可将其视为脆性材料。对于脆性材料，可采用第一强度理论对其进行强度设计［20］。结合第一强度理论的强度条件σ1=σt≤σb/n（σt为切应力，σb为材料的极限应力，n为安全系数）和式（3）可得内圈不产生塑性变形时所允许的最大压力pe为：

其中：

式中：σbi为淬火态内法兰轴的极限应力；ni为内法兰轴的安全系数，ni=2～3，本文取ni=3。

上述最大过盈量是基于静态破坏理论计算得到的，而在实际应用中，由于存在离心力、应力集中等情况，同时考虑到材料的不均匀性，需要设定一个安全系数。但是，目前轮毂轴承单元内圈与内法兰轴配合的过盈量的安全系数的取值尚无明确指引，本文取安全系数ns=2。则轮毂轴承单元内圈与内法兰轴配合的最大过盈量f0max为：

1.3 过盈量修正

1.3.1 考虑粗糙度和温度的过盈量修正

在实际设计轮毂轴承单元的过盈量时，不应忽略内圈与内法兰轴的表面粗糙度及温度等的影响。对于采用磨削加工工艺的内圈和内法兰轴，其表面粗糙度较小，则粗糙度对轮毂轴承单元内圈与内法兰轴配合的过盈量的影响可用式（10）来评估：

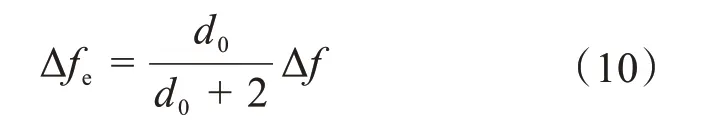
式中：Δfe为等效过盈量。

温度对轮毂轴承单元内圈和内法兰轴配合的过盈量的影响可用式（11）来评估：

式中：kT为温度修正系数，通常取kT=0.10～0.15；ΔT为轮毂轴承单元内圈与内法兰轴的温度差；α 为线膨胀系数。

根据实践经验，在粗糙度和温度的影响下，轮毂轴承单元减小的过盈量Δfc通常为0.004 mm。

1.3.2 考虑铆接装配的过盈量修正

在铆接装配后，轮毂轴承单元内法兰轴的轴端翻边并压覆于内圈上表面，由此内圈与内法兰轴轴端翻边之间形成轴向预紧力，如图2所示。该轴向预紧力在翻边贴合面处产生的静摩擦力可阻止内圈转动。设翻边贴合面处的轴向预紧力为Fc，则其产生的静摩擦力fc为：

式中：μc为内圈与内法兰轴轴端翻边之间的静摩擦系数。

联立式（2）、式（4）和式（12），可求得铆接装配后增大的过盈量Δf1为：

图2 铆接装配后内圈的受力示意图Fig.2 Schematic diagram of force on the inner ring after riveting assembly

另外，内法兰轴在铆接装配过程中的镦粗挤压作用也会导致过盈配合面的压力增大。设镦粗挤压作用下过盈配合面上增大的平均压力为Δpf，通过式（2）可计算得到因镦粗挤压作用而增大的过盈量Δf2为：

轮毂轴承单元的装配涉及复杂的材料、几何与接触非线性问题，难以准确和完整地采用解析法来建立其过盈量与各影响因素之间的定量描述关系。为此，本文拟采用数值模拟方法对轮毂轴承单元内圈与内法兰轴配合的过盈量进行修正。首先，采用有限元软件ABAQUS构建轮毂轴承单元过盈装配、铆接装配及铆接卸载回弹过程仿真模型；然后，通过数值模拟分析并获取铆接卸载回弹后内法兰轴轴端翻边贴合面处的轴向预紧力以及过盈配合面上增大的平均应力；最后，基于理论公式计算因铆接装配而增大的过盈量（Δf1+Δf2）。在过盈装配、铆接装配及铆接卸载回弹过程的数值模拟中，分别采用隐式—显式—隐式求解方法，具体流程如图3所示。数值模拟时建立的轮毂轴承单元有限元模型如图4所示。其中：在模拟过盈装配过程时，通过预设几何过盈量来实现内圈与内法兰轴的过盈装配加载；在模拟铆接装配过程时，在内圈底部施加固定约束，令铆头在绕其轴线转动的同时沿内法兰轴的轴线下移，直至移动到指定位置；在模拟铆接卸载回弹过程时，移除铆头，在固定内法兰轴底端的约束下实现轮毂轴承单元内应力的释放。

需要说明的是，在前期研究中，笔者已基于上述仿真模型对轮毂轴承单元内圈的变形行为及规律进行了研究，对应的试验结果表明上述仿真模型的预测精度良好［17］。因此，本文采用图3所示的数值模拟流程开展轮毂轴承单元过盈量修正计算是可行且可靠的。

图3 轮毂轴承单元装配过程数值模拟流程Fig.3 Numerical simulation flow of hub bearing unit assembly process

图4 轮毂轴承单元有限元模型Fig.4 Finite element model of hub bearing unit

综上所述，在修正轮毂轴承单元内圈与内法兰轴配合的最小过盈量时，需要考虑粗糙度、温度和铆接装配的影响，修正后的最小过盈量fmin为：

2 某型轮毂轴承单元过盈量设计实例

2.1 过盈量理论设计

以某型轮毂轴承单元为例，对其过盈量进行设计。该轮毂轴承单元关键零部件的主要尺寸如图5所示。其中，过盈配合面的有效宽度B=11.5 mm。

2.1.1 最小过盈量理论设计

在0.6g 加速度载荷下，轮毂轴承单元所受的径向载荷Fr=21.2 kN，径向额定静载荷C0r=43.3 kN。将上述参数代入式（6），可得该轮毂轴承单元内圈与内法兰轴配合的最小理论过盈量为：

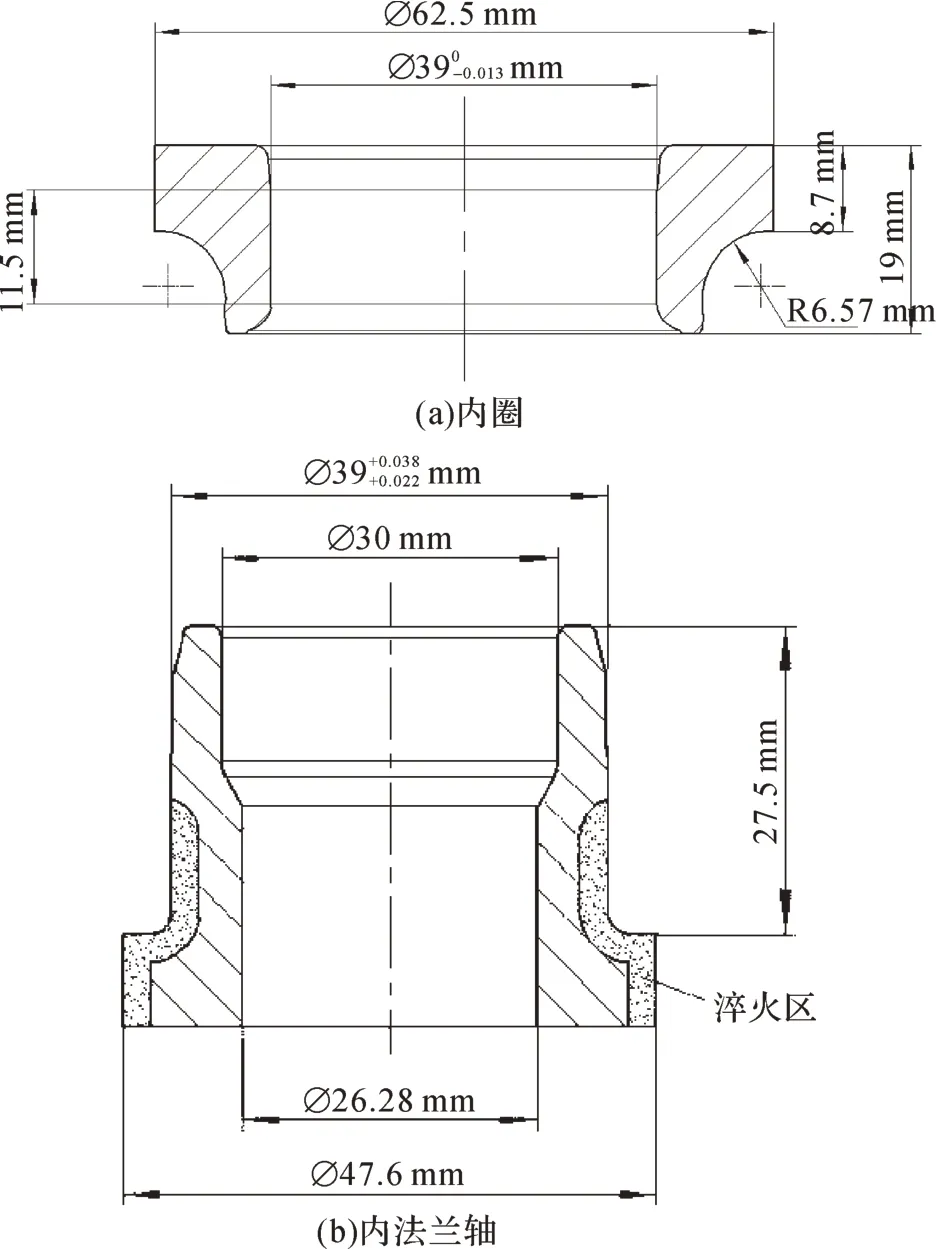
图5 某型轮毂轴承单元关键零部件的主要尺寸Fig.5 Main dimensions of key components of a hub bearing unit

2.1.2 最大过盈量理论设计

该型轮毂轴承单元内圈与内法兰轴材料的抗拉强度为1 700 MPa，将相关参数代入式（7）和式（8），计算得到pe=190.2 MPa，pi=167.7 MPa。将pe、pi中的较小者（167.7 MPa）代入式（9），求得该轮毂轴承单元内圈与内法兰轴配合的最大理论过盈量为：

2.2 考虑多个影响因素的过盈量修正

基于图3所示的数值模拟流程，对轮毂轴承单元装配过程进行数值模拟。结果表明：在工艺误差允许范围内，铆接装配后轮毂轴承单元内法兰轴轴端翻边贴合面的轴向预紧力Fc=10～20 kN，其产生的静摩擦力fc=1.5～3.0 kN。经计算，轮毂轴承单元内圈与内法兰轴配合的过盈量会增大0.006～0.012 mm，本文取较小值0.006 mm。

图6 和图7 分别为过盈装配和铆接卸载回弹后轮毂轴承单元内圈的应力分布云图。由图7（a）可知，过盈配合面附近区域的压应力比铆接前明显增大，尤其是过盈配合面上部，该处最大压应力为-320 MPa（负号表示压应力），而过盈配合面中部的压应力较小。由图7（b）可知，铆接后内圈的切向应力在过盈配合面起始处最大，为330 MPa，低于内圈材料的许用应力。提取铆接装配前后过盈配合面上各节点的平均径向应力并进行比较，结果显示平均径向压应力由铆接装配前的-43 MPa 增大至铆接装配后的-66 MPa。由式（14）计算可得，增大的过盈量Δf2=0.02 mm。

图6 过盈装配后轮毂轴承单元内圈的应力分布Fig.6 Stress distribution of inner ring of hub bearing unit after interference assembly

结合数值模拟结果和式（15）、式（16）可得，最终修正后轮毂轴承单元内圈和内法兰轴配合的最小过盈量和最大过盈量分别为：

3 试验验证

为了验证上述轮毂轴承单元过盈量理论设计方法的正确性，开展相关验证试验。准备5件轮毂轴承单元试件，按图5所示尺寸精磨其内圈内孔和内法兰轴，保证过盈配合尺寸接近设计值（误差小于0.003 mm）。具体试验过程如下：首先，将内圈与内法兰轴进行过盈装配并拔出，测量并记录压装力和拔出力；然后，再次将内圈与内法兰轴进行过盈装配，并按实际生产工艺进行铆接装配，装配完成后，采用车削方式去除内法兰轴轴端翻边，再将内圈拔出，测量并记录拔出力；最后，根据拔出力的变化量计算因铆接装配而增大的过盈量。试验结果如表1所示。由表1可以看出，内圈的平均拔出力从铆接装配前的16.92 kN 增大到铆接装配后的25.16 kN，增大了8.2 kN，相当于增大了0.017 mm 的过盈量，与上文所得的理论值0.020 mm 非常接近。此处需要说明的是，轮毂轴承单元试件直接从工厂生产线上获取，可能存在内法兰轴轴端高度、壁厚不一致的情况，这是导致因铆接装配而增大的过盈量存在差异的主要原因。

表1 轮毂轴承单元过盈装配及内圈拔出力测试数据Table 1 Test data of interference assembly and inner ring pull-out force of hub bearing unit

为进一步验证轮毂轴承单元过盈量理论设计方法的合理性，选取过盈量在上、下极限附近的轮毂轴承单元试件各3件，对其进行耐久试验。试件与试验设备如图8所示。基于业内耐久试验标准流程，对轮毂轴承单元试件施加径向载荷，循环周期为120 s，如图9 所示。整个耐久试验的测试时间为150 h，通过观察轮毂轴承单元内法兰轴轴端翻边是否发生周向蠕动来判断其内圈是否松动。试验结果显示：在下极限过盈量附近，内圈无松动；在上极限过盈量附近，内圈未破裂。由此说明，本文提出的轮毂轴承单元过盈量理论设计方法是合理的，其设计结果是可靠的。

图8 轮毂轴承单元试件与耐久试验设备Fig.8 Hub bearing unit test piece and endurance test equipment

图9 轮毂轴承单元耐久试验载荷加载周期Fig.9 Load cycle of endurance test of hub bearing unit

4 结 论

本文结合理论分析和数值模拟手段，提出了适用于工程实际的轮毂轴承单元过盈量理论设计方法。以某型轮毂轴承单元为例，对其内圈与内法兰轴配合面的过盈量进行理论设计和修正，得到内圈与内法兰配合的过盈量为0.015～0.049 mm。轮毂轴承单元内圈拔出力测量试验结果表明，因铆接装配而增大的过盈量的理论值与试验值接近，表明本文提出的方法是可靠的。过盈量在上、下极限附近的轮毂轴承单元试件的耐久试验结果显示，所有轮毂轴承单元试件均满足耐久试验要求，表明基于所提出的方法开展轮毂轴承单元过盈量设计可以满足工程要求。此外，还需要注意的是，在开展轮毂轴承单元过盈量设计时，要综合考虑安全性和经济性。在后续研究中，可从材料性能提升、铆接工艺优化和工序能力提升等角度来综合控制轮毂轴承单元的过盈量。