快慢车模式下基于扣除系数的线路通过能力研究*

吴金龙 丁小兵 刘志钢 赵 璐 张 鑫

(上海工程技术大学城市轨道交通学院， 201620， 上海∥第一作者， 硕士研究生)

在对城市轨道交通线路通过能力的诸多研究中，文献[1]研究了影响城市轨道交通线路通过能力的影响因素，并对各因素间的相互关系进行了深入分析；文献[2]对比研究了不具备越行条件时城市轨道交通线路快慢车组合运行情况，得出其与发车间隔、开行速度等因素间的相互关系；文献[3]构建了运营费用小模型，并巧用分枝定界法降低了模型的求解难度，得出固定运营周期内线路通过能力的近似可行解；文献[4]分析了不同开行比例及越行次数对线路通过能力的影响，对比研究了7种不同方案下线路的运能，并以上海轨道交通16号线为例验证了各方案合理性；文献[5]分析了不同越行次数、快慢车开行比例、发车间隔下的列车通过能力, 推断出线路通过能力的求解方法；文献[6]以哈尔滨地铁1号线的客流数据为基础，分析了客流分布对快慢车行车组织最大通过能力的影响；文献[7]通过测算以快车为主、以慢车为主2种运行模式下的在途停站时间，研究了这2种模式下系统能力的损耗情况。但是，目前业内对于快慢车运行模式下线路通过能力折损方面问题的研究相对较少，本文主要研究不同开行比例下快车对慢车的扣除系数，以及对线路通过能力的影响。

1 快慢车模式影响因素分析

1.1 快车对慢车的扣除系数

城市轨道交通线路通过能力计算公式为：

nmax=3 600/I

(1)

式中：

nmax——线路的最大通过能力，列/h；

I——列车发车间隔，s。

为研究快慢车模式下的线路通过能力，本文采用扣除系数法进行优化计算。选用慢车作为标准列车，先以慢车占用整条线路的能力作为标准，然后确定快车与慢车在能力占用上的比值关系，计算出线路通过能力损失的理论值，对其在不同行车组织条件下进行修正[8]。以站站停慢车为基础进行描述，铺画1对或1列快车从列车平行运行图(以下简称“平图”)上扣除慢车对数或列数，快车扣除系数εe的计算公式为：

εe=1+t差/I-k

(2)

式中：

εe——快车扣除系数；

t差——快车、慢车的单程旅行时间差，s；

k——慢车被越行的次数，次。

在实际的列车运行中，t差主要为快车因减少了停站时间及起停附加时间引起的单程旅行时间差。设快慢车的开行比例θ=e/s(e为快车列数，s为慢车列数)，在不考虑2列快车追踪运行的情况下，式(2)可以转化为：

εe=(Tc-I)/I-k

(3)

式中：

Tc——相邻的2组快慢车中每组的首列慢车的发车时间间隔，s。

快慢车运行可以看成是在全慢车运行中按照一定时间规律插入一定量的快车。快车的数量成为线路通过能力的主要制约因素，根据式(1)可以推导出快慢车模式下线路通过能力计算公式为：

n=3 600(s+e)/Tc

(4)

式中：

n——快慢车模式下的线路通过能力，列/h；

s——1个快慢车周期组合内慢车的数量，列；

e——1个快慢车周期组合内快车的数量，列。

本文主要研究在1个快慢车周期组合内插入1列快车的情况，则e=1。将式(3)代入式(4)，可得：

n=3 600(s+1)/[I(εe+k+1)]

(5)

相较于传统城市轨道交通线路站站停的运行模式，快慢车模式增大了列车行车间隔，导致快慢车间相互干扰，运能由此受到一定程度的影响。快慢车模式下的列车运行图为非平行运行图(以下简称“非平图”)，其线路损失通过能力、线路输送能力的计算如下：

nloss=nmax-n

(6)

P=nmp

(7)

(8)

式中：

nloss——快慢车模式下的非平图损失通过能力；

P——线路输送能力；

m——列车编组数；

p——列车定员数；

PKc——快慢车模式下单位小时内的线路输送能力；

1.2 快慢车越行的判定

由于快慢车运行速度及停站方案的差异性，区段内有快车越行慢车的可能性，是否越行可通过如下方法进行判断：如图1所示，与快车在车站不停站直接通过不同，慢车采用站站停的运行方式，慢车在车站增加了车站停站时间t起-停,其计算公式为：

t起-停=t制动+t停站+t启动

(9)

式中：

t制动——停车附加时间；

t停站——列车在车站的停站时间；

t起动——起动列车所需的附加时间。

图1 慢车进行车站停站作业时所需时间分解示意图

如图2所示，设采用快慢车模式的线路的始发站为A、终点站为X，车站数为j。前行列车为慢车，后行列车为快车，假定快车、慢车以相同速度运行。设快慢车在A站的发车间隔时间为Is,e，慢车停站次数为a(a=1,2,3，…,j-2)，则可按前、后列车到达某中间站的间隔时间是否大于或等于追踪间隔时间来判定是否越行：

(10)

图2 列车越行判定条件示意图

快车扣除系数的计算公式为：

εe=at停站/I+1

(11)

对于越行次数，当无越行时，线路通过能力较低；当有越行时，1个快慢车组合的周期变短。不同的快慢车比例下越行次数为1次、2次、3次、4次时，其越行示意图如图3所示。

注：实线表示慢车；虚线表示快车。

由此可见，一定的越行次数可有效提高线路通过能力。本文根据图3的快慢车比例及其越行次数，对非平图的线路通过能力进行研究。

2 采用扣除系数法分析非平图的线路通过能力

快慢车的开行比例是影响线路通过能力的1个重要因素，需根据客流需求予以决定。在不考虑越行位置的情况下，根据列车的越行条件，铺画了全慢车方案，以及快慢车开行比例分别为1∶1、1∶2、1∶3、1∶4时的开行方案，并对这5种方案的线路通过能力进行分析[5]。

2.1 方案1(全慢车方案)

采用方案1时，线路上没有快车，慢车采用站站停的运行方式，如图4所示。线路通过能力主要受I的影响，可根据式(1)进行计算。

图4 全慢车方案列车运行示意图

2.2 方案2(θ=1∶1)

方案2的快慢车列数相同。根据越行的判定条件，若存在部分慢车被越行，则存在线路通过能力损失的情况。在1个快慢车周期组合内，每越行1次，慢车的停站待避时间延长。仅考虑有1次越行时的运行图如图5所示。

图5 越行1次时的列车运行示意图(θ=1∶1)

在图5的列车运行图铺画方式下，线路通过能力的计算公式为：

Tc,1=I到通+Ie,s

(12)

εe=(Tc-I)/I-1=Tc/I-2

(13)

n1=3 600(1+1)/[I(εe+2)]

(14)

式中：

Tc,1——越行1次时相邻2组快慢车周期组合中每组首列慢车间的发车间隔,s;

Ie,s——前1个快慢车周期组合中快车与后1个快慢车组合中首列慢车间的发车间隔,s;

I到通——慢车到站等待快车越行的到通时间，s；

n1——越行1次时的线路通过能力，列/h。

2.3 方案3(θ=1∶2)

方案3相当于在方案2的基础上每个运行单程内插入1列慢车，此时存在2种列车越行的情况：图6为前行的1列慢车被后行快车越行的列车运行示意图；图7为前行的2列慢车被后行快车越行的列车运行示意图。

图6 越行1次时的列车运行示意图(θ=1∶2)

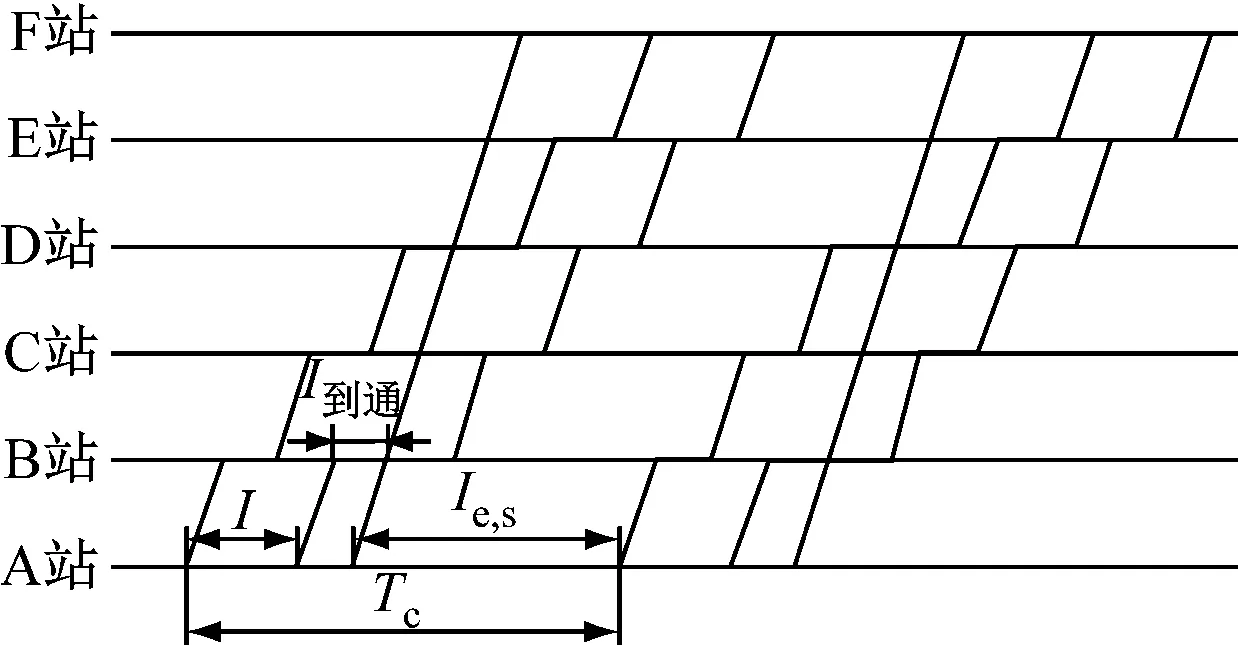
图7 越行2次时的列车运行示意图(θ=1∶2)

方案3的线路通过能力计算如下：

Tc,2=I+I到通+Ie,s

(15)

εe=(Tc-I)/I-2=Tc/I-3

(16)

n2=3 600(2+1)/[I(εe+3)]

(17)

式中：

Tc,2——越行2次时相邻2组快慢车周期组合中每组首列慢车间的发车间隔,s;

n2——越行2次时的线路通过能力，列/h。

2.4 方案4(θ=1∶3)

方案4下越行次数为1次和2次时的εe与方案3相同；越行次数为3次的列车运行图如图8所示。

图8 越行3次时的列车运行示意图(θ=1∶3)

方案4的线路通过能力计算如下：

Tc,3=2I+I到通+Ie,s

(18)

εe=(Tc-I)/I-3=Tc/I-4

(19)

n3=3 600(3+1)/[I(εe+4)]

(20)

式中：

Tc,3——越行3次时相邻2组快慢车周期组合中每组首列慢车间的发车间隔,s;

n3——越行3次时的线路通过能力，列/h。

2.5 方案5(θ=1∶4)

方案5在越行次数为1次、2次、3次时的εe与方案4相同。越行次数为4次的列车运行图如图9所示。

图9 越行4次时的列车运行示意图(θ=1∶4)

方案5的线路通过能力计算如下：

Tc,4=3I+I到通+Ie,s

(21)

εe=(Tc-I)/I-4=Tc/I-5

(22)

n4=3 600(4+1)/[I(εe+5)]

(23)

式中：

Tc,4——越行4次时相邻2组快慢车周期组合中每组首列慢车间的发车间隔,s;

n4——越行4次时的线路通过能力，列/h。

3 快慢车模式下线路通过能力实例分析

选取上海轨道交通16号线为案例对线路通过能力进行研究。该线全长58.96 km，与本研究相关的运营情况主要有：

1) 列车为A型车，定员216人/辆，设计速度为120 km/h；

2) 快、慢车均采用6节编组，且有足够车底；

3) 慢车的发车间隔时间为150 s。

根据式(1)，可计算得到平图的线路通过能力n为24列/h。

列车的实际运行中，在始发站采用“前慢后快”的发车方式，Is,e为240 s，t起动、t停站合计耗时20 s，I到通为60 s，Ie,s为270 s。由此可计算出上述5个方案下的扣除系数εe及线路通过能力，如表1所示。

表1 不同快慢车开行方案下的扣除系数及线路通过能力

从表1可以看出，随着快慢车开行比例的增大，损失的线路通过能力呈现下降趋势。当慢车所占比例提高，且数量多于快车时，线路通过能力逐渐提高。θ=1∶4时，损失的线路通过能力最小，线路通过能力最大。应根据该线的客流分布特征来选择快慢车的开行比例。

由式(7)、(8)可以得到16号线高峰时段(7:30-8:30)不同快慢车比例下的线路输送能力，如表2所示。

表2 不同快慢车开行比例下16号线的线路输送能力

根据AFC(自动售检票)数据，16号线工作日高峰小时最大断面客流超过3万人次/h。结合表3可以得出结论： 16号线在高峰时段宜采取1∶4的快慢车开行比例。

4 结语

本文对铺画的5种方案进行计算,结果表明：线路的实际通过能力会随快慢车开行比例的变化而变化。在高峰时段，线路的实际通过能力随着开行比例的加大而逐渐提高。在开行比例为1∶4时，实际的线路通过能力达到最大。结合上海轨道交通16号线高峰时段(7:30—8:30)的客流需求，对比分析得到此比例即为线路的最佳开行比例。采用最优的快慢车开行方案，既可满足客流需求，也不会导致列车虚糜率上升，具有一定的社会效益。