基于有限元分析和机器学习的跌落所致封装结构力学行为预测

张筱迪，毛明晖，卢昶衡，王文武，贾冯睿，龙 旭

（1.辽宁石油化工大学土木工程学院，辽宁抚顺 113001；2.西北工业大学力学与土木建筑学院，先进电子封装材料与结构研究中心，西安 710021；3.浙江清华长三角研究院，浙江嘉兴 314006）

1 引言

电子封装本质是其对集成电路芯片的电气特征保持功能、机械保护功能和应力缓和功能，随着科技进步和社会发展，封装将面临着更加严苛的工作条件。电子设备的小型化和无铅化趋势要求封装结构具有更优化的力学性能及更高的结构可靠性，这驱使封装向高集成方向发展，主要体现在焊料微互连向小尺寸和超细间距方向发展。电子产品在使用过程中经常存在跌落情况，而跌落过程会导致焊点承受与正常工况显著不同的应力情况，从而可能导致焊点断裂进而失效。此过程涉及到板级封装在跌落冲击载荷下的失效机理分析、焊料微互连的应力应变响应分析和动态响应分析。

由于板极跌落具有更高的可操作性，目前跌落冲击试验主要研究了板极跌落。ABAQUS 有限元隐式或显式动力学分析方法已被广泛应用于对跌落冲击过程的数值模拟。LIM 等[1]利用ABAQUS 显式分析模拟了寻呼机的跌落冲击动力响应；WONG 等人[2]研究了在跌落冲击载荷下PCB 板的基本动力学原理；VARGHESE 和DASGUPTA[3]发现，在诸多影响因素中，对钎料焊点冲击性能影响最为重要的是过载冲击力和应变大小。TEE 等[4]提出了应用Input-G 的等效加速度方法来模拟电路板在跌落过程中的边界条件。尽管最近有大量工作致力于在电力电子设备[5-8]中使用人工智能，但只有很少一部分应用于电子系统中焊点的可靠性和寿命预测。VAHID 等[9]基于传统的人工神经网络开发了一种相关驱动神经网络（CDNN）机制，用于评估电子系统中焊点的可靠性，该模型根据材料属性、设备配置和热循环变化来预测使用寿命。结果表明预测模型在尽可能短的时间内具有很高的准确性。DING 等[10]提出了一种用于EBSD 模式索引的神经网络（EBSD-CNN），并描述了必要的数据准备和模式预处理，揭示了神经网络在EBSD 模式索引中的潜力。YI 和JONES[11]在最近的工作中，证明了通过人工智能机制预测的故障模式比传统的统计方法要准确得多。SHIRAIWA 等[12]采用了基于模型的机器学习技术，并考虑疲劳寿命的不确定性来预测结构的疲劳性能，表明基于模型的机器学习是预测结构材料疲劳性能的有潜力的工具。本文将利用商业有限元软件ABAQUS对板极BGA 封装结构在跌落冲击下的动力响应进行数值模拟，获取用于训练预测模型的数据组并建立机器学习（Machine Learning，ML）方法预测评估封装结构力学可靠性。在以后的研究中解决类似多场耦合时评估焊点可靠性问题时可以直接应用机器学习来模拟并预测，而不再使用有限元模拟。

2 板级电子封装跌落冲击的数值仿真及结果讨论

作为一个典型封装结构，PBGA 封装芯片示意图如图1 所示，三维有限元模型依此建立，其中芯片、模塑料、基板均为正方形。基板尺寸为42 mm×42 mm×2.5 mm。芯片通过焊点阵列与基板焊接于基板的中央。芯片尺寸为20mm×20mm×2.2mm，焊点直径2mm，高为1.8 mm，焊点间距为3.0 mm。焊点之间用填充物填充。模塑料尺寸为38 mm×38 mm×5.5 mm。相关材料力学参数由表1 给出。

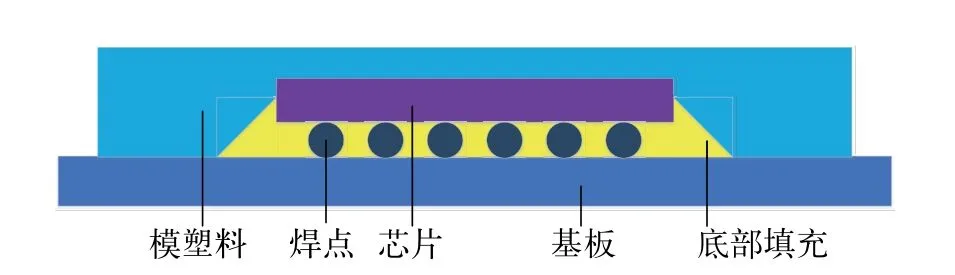
图1 PBGA 封装结构示意图

表1 有限元模型中材料参数

本文所用焊料材料为SAC305，其本构曲线如图2所示。不同的应变率下，材料本构模型对应不同的应力-应变曲线。由于本文研究重点为机器学习算法的训练以及对封装结构应力及变形的预测，因此本文暂未考虑材料的应变率效应。如果考虑应变率效应，可以参考本课题组已发表的其他研究工作[13]。其中PBGA 封装整体模型及焊点网格划分如图3 和图4 所示。

图2 焊料本构曲线

图3 焊点网格划分

图4 PBGA 封装结构网格划分

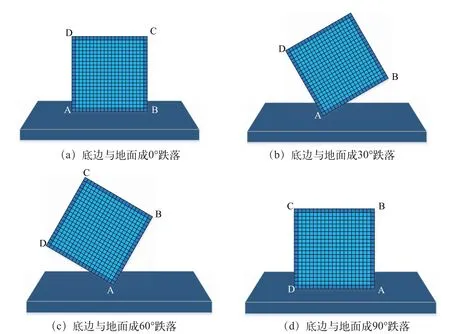
图5 ABAQUS 模型仿真的跌落形式

在实际使用过程中，微型电子器件会有多种不同的跌落工况出现，跌落方式的不同将导致失效焊点的位置和顺序依次变化。如图5 所示，本文主要研究以下4 种封装结构边缘与刚性面相接触的跌落形式：（a）底边与地面成0°跌落；（b）底边与地面成30°跌落；（c）底边与地面成60°跌落；（d）底边与地面成90°跌落。通过控制变量法，分别研究这几种跌落方式在0.8 m、1.0 m 和1.5 m 跌落高度下的动力响应，跌落接触的地面假设为刚度无穷大的刚性面，不产生任何变形。

跌落后结构整体应力云图如图6 所示。研究发现，应变率对焊点的应力应变演化有显著影响。BGA 结构首次接触到地面为t=0 s 时刻，由数值模拟结果得知焊点分别在t=2.2602×10-4s、t=2.2803×10-4s和t=2.2901×10-4s时的Von Mises 等效应力如图7～9 所示。因结构为双轴对称结构，90°跌落与0°跌落的相关动力响应相同，因此此处不再列出其应力云图。可以看出，跌落方式对封装结构内部应力演化有显著影响。在与地面刚开始接触时，离接触面最近的一排焊点应力最先开始增大，这一排的焊点均最先达到临界应力，接着后面焊点应力依次增大。

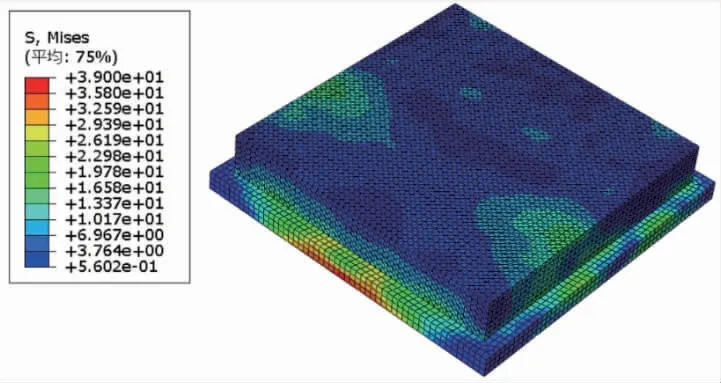
图6 跌落后封装结构应力云图

图7 从1 m 高度跌落后不同时刻焊点Mises 等效应力（底边与地面成0°角）

图8 从1 m 高度跌落后不同时刻焊点Mises 等效应力（底边与地面成30°角）

图9 从1 m 高度跌落后不同时刻焊点Mises 等效应力（底边与地面成60°角）

由图7 可见，在t=2.280×10-4s时，达到临界应力的焊点数量几乎占到总数量的一半，在t=2.2901×10-4s时几乎全部焊点达到应力最大状态。当跌落角度为0°和90°时，跌落所致封装结构应力比30°和60°角度跌落模式大，并且应力增长较快。这是由于跌落方式为非对称，而第二种和第三种跌落经历了较长的应力缓冲时间，结构其他部件消耗了较多的能量，对焊点而言其加载率就最小，应力增长也就更慢。

在实际微电子设备跌落冲击的情况下，从空中跌落的角度和高度是随机的，无法实现准确的跌落形态预测，在本文模拟中简化该工况问题。通过控制变量法，从跌落冲击位置、跌落冲击高度等方面，通过所建立的有限元模型开展参数分析。我们从数值模拟中观察到处于碰撞第一排角点的焊点最先达到应力值，离碰撞面越近其应力值相应越大。这与已有研究结果[13]保持一致。其中，在冲击载荷作用下封装器件会发生自由变形，固化后的焊点会在器件屈曲变形时受到拉压变形，因此基板在跌落时发生的屈曲变形也会影响焊点的应力应变演化。因此，本文选取图10 所示黑色焊点为训练数据来源对象，耦合各变量值后共计选取11×4×3 组点位及其对应的Mises 应力和等效塑性应变PEEQ 值为研究对象，结合机器学习方法，将各点位的应力和PEEQ 作为训练模型的预测目标。

图10 焊点分布位置（训练数据源自黑色焊点有限元计算结果）

3 有限元计算结构的机器学习及结果讨论

3.1 机器学习过程

在热-力耦合过程中，焊点故障演变中涉及的参数数量和种类繁多，导致电子设备的可靠性评估缓慢而昂贵。为了应对这一挑战，相关研究提出一种用于评估电子封装结构抗跌落可靠性的机器学习框架，即相关性驱动的神经网络模型。

如图11 所示，机器学习模型的训练和预测过程分为5 个主要步骤。在数据收集过程和输入输出特性描述之后，提出影响焊点应力演化的跌落方式的主要特征变量，本文所处理问题的关键变量包括跌落角度、跌落高度和跌落速度。下一步是使用机器学习算法来训练预测模型，以估算有效焊点的应力和PEEQ 值。足够多的输入数据的收集，在训练模型过程中起着重要作用。所有收集的数据都是从有限元模型（FEM）模拟结果中提取的，所有参数的单位均已统一。在选取输入特征量时，需要对模型的描述足够全面。本文中将跌落角度、高度和焊点点位坐标作为输入特征量构建了一个12 维向量作为一组数据组，12 个输入特征量的具体选择如表2 所示。其中，点的坐标通过以左下角点为原点的直角坐标系来进行计算。对于每组模拟，从焊点阵列中11 个不同独立焊点位置提取数据，形成包含约132 组12 维向量的数据集。以跌落角度与地面夹角为30°、跌落高度为0.8 m、焊点坐标为（1，1）、目标值为PEEQ 为例，这一组数据的形式为（30，60，90，0，4000，0，800，1，1，1.211×10-3,0,0），数据依次代表用于神经网络训练的12 个输入特征量的具体取值。

图11 CDNN 模型的数据传递图

表2 封装结构抗跌落可靠性评估的关键特征变量

有很多ML 算法，例如线性ML 算法、非线性ML算法和集成ML 算法等，本文所采用人工智能算法为相关驱动神经网络（CDNN），它能够合理捕获候选特征之间的相关性。借助CDNN 模型，可以在输入（或特征）和输出（目标）之间建立更准确的预测模型（f），以评估电子设备中焊点的力学参数。

本文机器学习部分的工作使用CDNN 神经网络方法进行，使用不同的学习方法需要对不同的参数进行设置，对于CDNN 方法主要参数为特征缩放，以对候选特征进行归一化，利用最小-最大重新缩放公式将特征候选重新缩放到[0，1]的预定范围。此外，CDNN神经网络方法包含隐藏层数和隐藏层单元数等参数，决定了模型所能学习数据的复杂程度，也影响模型是否能达到最优解，其中，训练后得到最优神经网络结构，其矩阵传递关系权重如图12 所示（由于过滤器放大了矩阵，过大矩阵不便以表格形式表示，因此以三维曲面图的形式呈现，其中x轴表示的是权重矩阵中的行数，y轴表示的是权重矩阵中的列数，z轴表示权值）。

获取训练所需有效数据后，针对应力与应变分别训练不同的模型，另外用准确度r2=1-u/v判断模型质量好坏。式中u为真实值和预测值的差的平方和，v为真实值和真实平均值的差的平方和。

图12 训练后得到的最优神经网络结构的各参数权值

3.2 结果分析与讨论

相比于有限元计算焊点跌落过程中的应力演化所需时间，使用神经网络方法学习时间约为2 min，在计算速度上具有明显的优势。由图13 和图14 可以看到CDNN 方法训练所得模型对焊点应力和等效塑性应变的演化趋势和ABAQUS 模拟结果是基本相同的。神经网络方法对焊点等效塑性应变、应力学习模型的准确度r2分别为0.924 和0.946，可以看出所预测的模型具有较高精度。

但同时从图14 中也可以看出有一些偏差较大的点，这是由于在机器学习过程中进行了2 次卷积，而在卷积过程中零乘以任何数据值都为零，这不可避免地导致这些时刻对应的权值随机过大或过小，从而导致预测结果与真实值产生较大偏差。但从整体来看，基于机器学习的算法预测值与有限元软件的计算值之间相关性在80%以上，因此总体而言，机器学习的算法预测值还是相对可靠的。综上所述，预测结果表明CDNN 模型能在足够的范围内保证预测精度，可见其具有良好的预测效果。

图13 神经网络方法在测试集上的部分预测结果

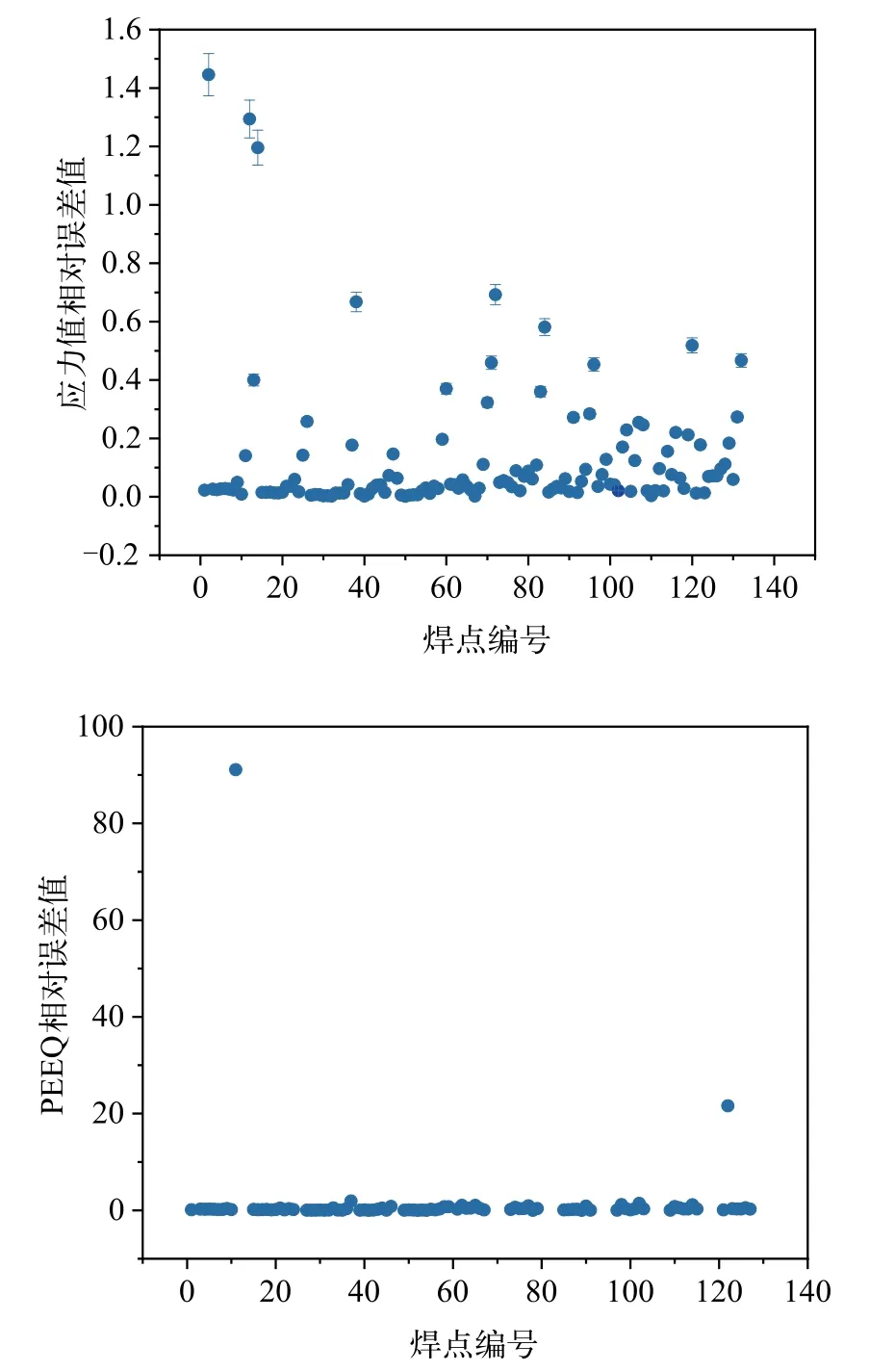
图14 相对误差

4 结论

本文针对PBGA 板极封装结构，从研究不同跌落工况下各点位焊点的动力响应问题出发，通过结合ABAQUS 有限元数值模拟和机器学习方法，采用控制变量方法研究了多种工况下焊点的应力应变演化情况，并验证了CDNN 预测模型的准确性。主要结论如下：

（1）数值模拟结果表示结构在跌落过程中应力首先从接触面位置开始增大，并且角点位置焊点应力应变数值最大。跌落所致的封装失效主要是由于焊点达到临界应力失效所致。

（2）在通过ABAQUS 数值模拟获取基本的数据后，通过机器学习方法提取输入特征参数来建立神经网络预测模型，可以替代有限元实现对焊点应力应变演化结果的预测，训练模型所需的计算时间远低于有限元模拟计算的时间，并且CDNN 模型能较好地预测各种工况下焊点各点位的力学性能参数，预测结果具有较高的精确度。因此，在研究封装结构跌落动力响应时应用机器学习方法可以起到简化复杂的建模流程和提高计算速度的目的。

（3）虽然本文使用机器学习方法研究了PBGA 封装跌落的动力响应，但其计算流程是具有普适性的。对于其他受力模型如温度循环及机械循环寿命预测模型等也可以采取类似的办法。将机器学习方法应用到诸如此类的研究中去，可以达到简化建模和提高计算速度的目的。

本文提出的预测模型还未考虑封装结构几何尺寸以及材料特性等参数，并且计算结果具有不可避免的随机性，这仍需在未来研究中继续探索。总体来说，本文结果表明，基于有限元仿真模型的机器学习方法，在预测封装结构复杂工况下力学性能可靠性方面具有良好的适用性和深入开发的巨大潜力。