混合交通环境车辆队列协同控制
杨依琳,边有钢,胡满江,杜长坤,徐 彪,秦兆博
(1.湖南大学 机械与运载工程学院,湖南 长沙 410082;2.北京理工大学 机电学院,北京 100081)
0 引言
汽车保有量的增加对道路容量、交通安全和通行效率提出了更高要求,智能网联车辆技术为解决这一问题提供了有效手段。车辆队列协同控制即为这一技术的重要应用,其可通过车载传感器和车车(vehicle-to-vehicle, V2V)通信保证车辆之间近距离稳定跟驰,进而有效降低风阻、提升燃油经济性、提高交通流量。
现有队列控制相关研究多假设所有车辆均为智能网联车辆(intelligent connected vehicle, ICV),称为完全智能网联车辆队列。目前,国内外针对完全智能网联车辆队列已有许多研究。文献[1]提出一种分布式模型预测控制设计方法,研究了队列闭环稳定性及鲁棒性;文献[2-5]将队列的稳定性分析与控制器设计拓展到了不同跟踪策略与通信拓扑中。然而,车辆的智能化、网联化过程是循序渐进的,人们必将面对混合交通情况;由于混合车辆队列的复杂性,目前对混合车辆队列的研究较少。文献[6-7]研究了通信拓扑结构与时延对交通稳定性的影响。文献[8]利用机器学习等更复杂的策略提升队列性能。文献[9-10]研究证实了单个智能网联车辆在环形道路中稳定整个交通流的潜力。根据其他性能指标,文献[11-12]将车辆跟踪性能、燃油经济性纳入考虑的控制系统研究中。
现有针对混合车辆队列的研究大多仅考虑前车信息,研究重点在于保证车辆的稳定跟驰,而未考虑智能网联车辆对后方交通流的影响,对后车信息利用也不充分。实际上,后车信息对提升车辆队列性能也非常重要[13]。此外,现有研究多关注车辆队列稳定性,对队列综合性能考虑较少。为此,本文研究智能网联车辆与人工驾驶车辆(human-driven vehicle, HDV)共存的混合交通环境中车辆队列控制问题,重点研究考虑后方车辆信息的控制器设计;并基于数值仿真,分析该控制器对车辆跟踪性能、燃油经济性、交通流稳定性的影响。
1 混合车辆队列系统建模
对所研究的混合车辆队列进行建模:首先描述混合车辆队列系统模型,即建立人工驾驶车辆与智能网联车辆模型;其次,在此基础上为智能网联车辆设计同时一种考虑前后车信息的控制器。
1.1 混合车辆队列
如图1所示,本文考虑由(n+1)辆车组成的混合车辆队列,其中仅包含一辆智能网联车辆,其他均为人工驾驶车辆。通过传感器和V2V通信技术,队列中部分车辆能相互传递信息。

图1 混合车辆队列系统模型Fig.1 System model of the mixed vehicular platoon
1.2 人工驾驶车辆模型
本文采用经典的最优速度模型(optimal-velocity model, OVM)模型[7,9-10]来描述人工驾驶车辆的纵向动力学性能:

式中:si,vi——车辆i的位置和速度;hi(t)——车辆i与前车的距离,hi(t)=si-1(t)-si(t);αh和βh——驾驶员反应参数;V(h)——车辆期望速度函数。
V(h)通常由如下分段函数表示:

其中F(h)连续且单调递增,其有多种形式,本文采用以下典型非线性形式[6,9]:

式(2)和式(3)即经典的OVM模型,其实质是一种距离控制策略:车距h小于等于hst时,停车;车距大于等于hgo时,车辆以最高速度行驶。OVM模型中的车辆期望速度函数V(h)波形如图2所示。
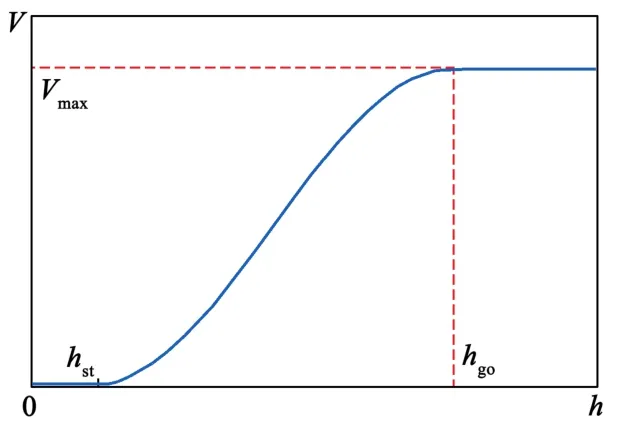
图2 OVM模型中期望速度函数波形Fig.2 Diagram of OVM desired velocity function
车辆队列的期望状态是所有车辆保持相同的速度且有恒定车距,表示为

根据式(4),车辆距离和速度的跟踪误差可分别表示为

定义车辆i的位置误差,由此将式(1)在(h*,v*)处线性化,得到车辆i的速度误差:
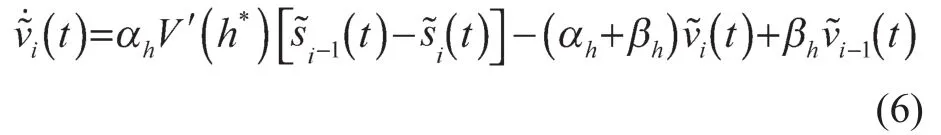
式中:V′(h*)——V(h)在h=h*处的导数。
1.3 智能网联车辆模型
1.3.1 车辆纵向动力学模型
将智能网联车辆的加速度响应近似为一阶惯性环节,其纵向动力学采用式(7)所示线性三阶状态方程[1,3-4]描述。
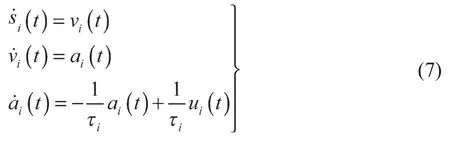
式中:ui——车辆i的控制输入,相当于车辆期望加速度;τi——车辆动力系统的时滞常数;ai——车辆i的加速度。
1.3.2 车辆控制器模型
根据式(4)车辆队列的控制目标构造位置误差与速度误差:

由于本文研究的智能网联车辆同时考虑了前后车信息,故设计了一种适用于双向信息流拓扑结构的控制器,它是基于网联巡航控制模型[6]及OVM模型[9]而改进的。图1为本文所研究的混合车辆队列,其中唯一一辆智能网联车辆可以获取紧邻的前p辆和后q辆车信息。
智能网联车辆非线性控制器设计如下:

式中:αi,j和βi,j——车辆i与车辆j之间的距离控制增益、速度控制增益,此处设定匀质的控制增益,即αi,j=α,βi,j=β;hi,j——车辆i与车辆j的平均车距,;l——车辆长度;Vi,j(hi,j)——车辆期望速度函数。
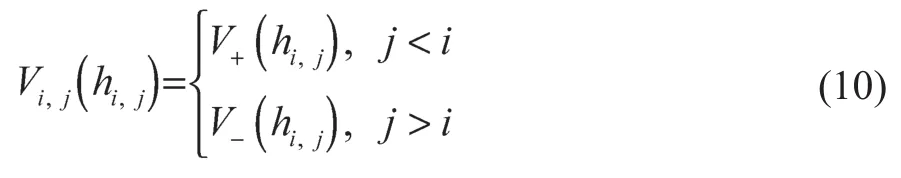
Vi,j(hi,j)由OVM模型改进而来。当车辆获得的信息来源于前方车辆时,V+(hi,j)=V(hi,j),与OVM模型一样,即式(2);当车辆获得的信息来源于后方车辆时,控制策略不同,期望速度函数需要改变,设计为“逆”OVM模型V-(hi,j),其表达式如下:
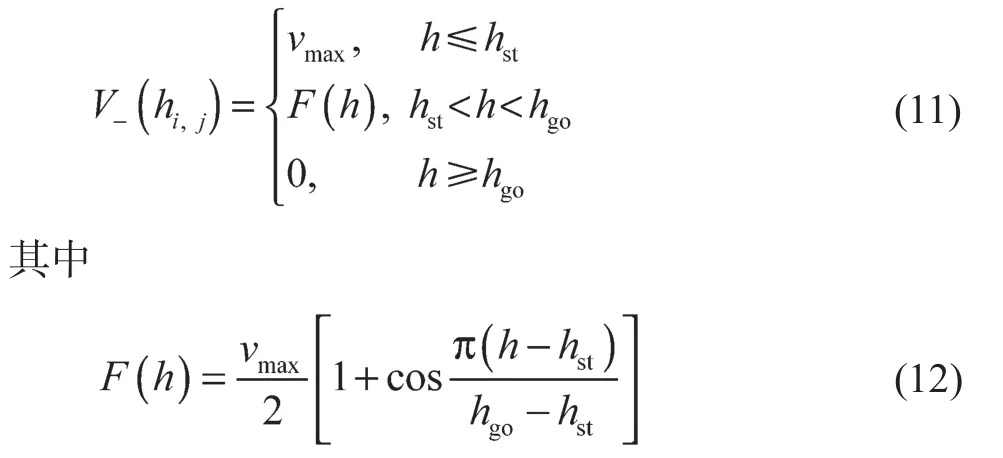
函数F(h)连续且单调递减,这意味着智能网联车辆跟踪前方车辆和后方车辆时跟车策略是相反的。改进后的模型中两种期望速度函数波形如图3所示。

图3 改进模型中的期望速度函数Fig.3 Desired velocity function in the modified model
2 混合车辆队列稳定性分析
对所提出的考虑后车信息的混合车辆队列系统模型进行稳定性分析:先给出车辆队列稳定性定义,然后依据迭代的思想提出一种适用于双向信息流拓扑结构的方法计算首尾传递函数,最后给出队列闭环稳定及队列首尾稳定的条件。
2.1 稳定性定义
定义1闭环稳定性
在没有外界干扰情况下,车辆队列控制系统可达到渐近稳定,即队列闭环稳定。
定义2队列首尾稳定性
扰动作用于头车时,如果扰动在到达尾车时减弱,则队列首尾稳定。
2.2 首尾传递函数计算
首尾传递函数Gn,0(s)即头车到尾车的速度误差传递函数,其描述了扰动的动态关系。本文先通过计算得到Gn,0(s)所需的链路传递函数Ti,j(s),进而给出Gn,0(s)的计算方法。
2.2.1 智能网联车辆链路传递函数的计算
为计算Ti,j(s),先对车辆纵向动力学模型进行线性化处理。由于车辆队列期望状态为(h*,v*),根据式(7)和式(8),则控制器模型式(9)可进一步被改写为

根据式(11),对式(13)在平衡点(h*,v*)处线性化,得

其中V′i,j(h*)为Vi,j的导数。
令
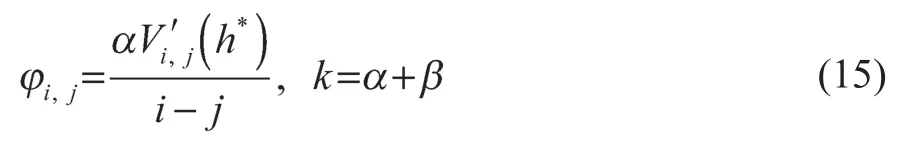
设定vmax=30 m/s,hst=5 m,hgo=35 m,h*=20 m,v*=V(h*)=15 m/s,则根据式(11)可知

至此,对非线性控制器的线性化处理已完成。
由式(7)和式(8)可得

将式(17)代入式(14),则:

为方便推导Gn,0(s),得到队列首尾稳定性条件,本文将式(18)由时域转化到频域中描述。假设零初始状态,式(18)经拉普拉斯变换得

整理式(19),可得

式中:Ti,j(s)称为链路传递函数,可以理解为车辆i速度误差频域描述中车辆j速度误差对应的权重。
2.2.2 人工驾驶车辆链路传递函数的计算
设人工驾驶车辆的链路传递函数为Th(s),其计算更简单,相当于p=1,q=0的特殊情况,且不存在控制器输入。针对人工驾驶车辆i,有Ti,j(s)=Ti,i-1(s)=Th(s),则可知

2.2.3 首尾传递函数的计算
Gn,0(s)在不同文献中有着不同的计算方法,但大部分均以智能网联车辆跟驰前车为前提,未考虑后车信息。这里提出一种基于迭代思想[13]、适用于双向信息流拓扑结构的Gn,0(s)计算方法。
假设整个混合车辆队列共(n+1)辆车,可将Gn,0(s)表述为

其中,Gn,0(s)中包含了0车到n车之间所有车辆的纵向动力学。
假设k车是智能网联车辆,其他均为人工驾驶车辆,则由式(22)可知

将式(25)代入式(20),得

将式(26)代入式(20)和式(24),即可得到首尾传递函数Gn,0(s)。
2.3 队列闭环稳定性及首尾稳定性
基于首尾传递函数,头车速度扰动将被按比率|Gn,0(s)|放大到尾车,s=jω,,ω为速度扰动的频率。因此,队列首尾稳定条件为

3 仿真分析
为验证本文所提出控制器的有效性,本文在Matlab/Simulink平台下进行数值仿真,以分析混合车辆队列的稳定性、跟踪性能和油耗情况。
仿真中考虑包含7辆车的混合车辆队列,其中只有第4车是智能网联车辆,其可获得紧邻的前p辆、后q辆车信息。选取p=2,q=1以及p=2,q=0两种信息流(即是否考虑后车信息)情况进行仿真。仿真工况为头车扰动工况,其速度呈正弦波动。为得到车辆油耗数据,仿真采用非线性动力学模型,使用逆模型补偿方法[2]建模,非线性模型参数设置见表1。

表1 队列中的车辆参数Tab.1 Vehicle parameters of the vehicular platoon
3.1 稳定性分析
根据人工驾驶车辆链路传递函数Th(s)及队列首尾稳定性条件,可得驾驶员反应参数αh和βh的稳定域,如图4所示。依据对驾驶员驾驶行为的研究[14],驾驶员反应参数选取αh=0.6,βh=0.6,此参数不在稳定域内,即扰动经过人工驾驶车辆会被放大。

图4 驾驶员反应参数稳定域图Fig.4 Stability diagram of the reaction parameters of human drivers
由式(26)可计算得到p=2,q=1情况下队列首尾稳定的稳定域,如图5所示。取α=1,β=1.5进行仿真,即图5中A点。在p=2,q=0情况下,不存在首位队列稳定域,即在智能网联车辆只获取前2辆车信息情况下,无论控制器参数如何设计,都无法保证队列首尾稳定性。
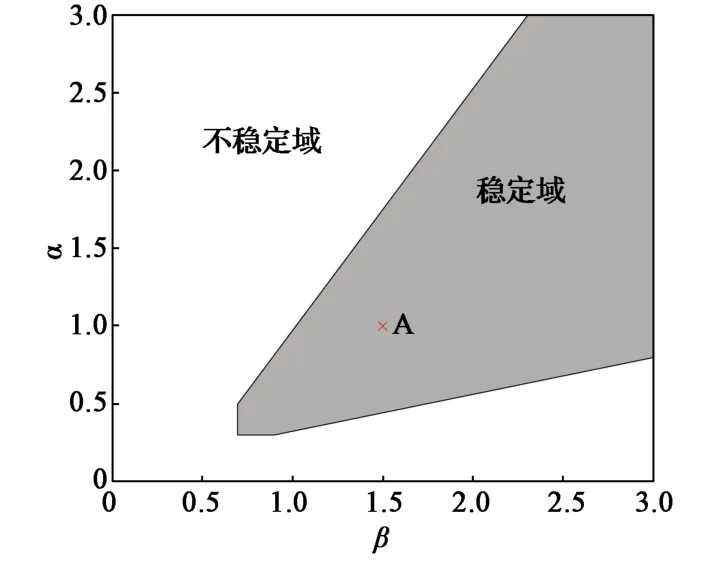
图5 p=2, q=1时车辆队列稳定域图Fig.5 Stability diagram of vehicular platoons as p=2, q=1
采用A点控制器参数进行队列仿真,结果如图6所示,其中速度误差幅值比-频率曲线代表对应两车之间速度误差的幅值比与速度扰动频率的关系。可见,q=0时,队列首尾稳定性无法被保证,第6车传递函数幅值超过1,其速度振动幅值也超过领航车;q=1时,队列首尾稳定,第6车传递函数幅值小于1,后方车辆扰动明显减小,且头车传到尾车的扰动也减小。这表明,混合队列中智能网联车辆的双向信息流拓扑结构有利于扰动衰减,保证队列首尾稳定。

图6 误差频域响应图与速度图Fig.6 Bode plots and velocity responses
3.2 跟踪性能分析
设置智能网联车辆控制器参数α=0.8,β=1.2,可保证车辆队列首尾稳定性。扰动工况下混合车辆队列仿真结果如图7和图8所示,可见智能网联车辆获得紧邻的后车信息后,后方车辆的速度波动与距离误差明显减小。

图7 速度图Fig.7 Velocity responses

图8 距离误差图Fig.8 Spacing error
下面对此仿真结果进行定量分析。定义跟踪误差(tracking error index, TEI)[11-12]指标:

式中:T——仿真时间;Δd——距离误差;Δv——速度误差。
在考虑与不考虑后车信息的两种情况下,智能网联车辆及其后方车辆累计跟踪误差如图9所示。由图9可见,在考虑后半信息情况下,后方车辆跟踪误差显著减小,而智能网联车辆(第4辆车)跟踪误差增大。

图9 累计跟踪误差图Fig.9 Total tracking error
由累计跟踪误差计算结果(表2)可知,考虑后方车辆信息时,智能网联车辆自车的跟踪误差会增大(因为其前车有较大的扰动,而自车扰动衰减,故其与前车距离误差明显增大,跟踪误差随之增大),而后方车辆的跟踪误差减小了30%,因此整体来说后方队列的跟踪性能有明显提升。

表2 跟踪误差指标Tab.2 Tracking error index
3.3 油耗性能分析
依据智能网联车辆动力学非线性模型[2]仿真,得到在考虑与不考虑后车信息情况下智能网联车辆及其后车的累计油耗情况(图10),可见车辆油耗均有所降低。

图10 累计油耗Fig.10 Total fuel consumption
定义每公里平均油耗(fuel consumption per kilometers, FCM)指标[11-12]:

式中:S——自车行驶路程;Qeng——燃油消耗率。
累计油耗结果见表3。由表3可知,当智能网联车辆考虑后车信息时,车辆整体油耗总和降低了0.6%,这是因为考虑后车信息有利于衰减扰动,加减速不再那么剧烈,故油耗也有所降低。

表3 平均油耗Tab.3 Average fuel consumption
4 结语
本文研究混合交通环境下车辆队列协同控制:在智能网联车辆控制中引入后车信息并分析了其对后方交通流的影响;基于已有的混合车辆队列系统模型,改进设计了一种适用于双向信息流拓扑结构的智能网联车辆控制器。仿真结果表明,利用后车信息可有效衰减队内扰动,保证队列稳定,改善队列跟踪性能和车辆整体的油耗性能;同时,智能网联车辆作为混合车辆队列中的可控单元,可有效地衰减队内干扰,提高交通流量,提升燃油经济性。
本研究仅考虑了固定参数的人类驾驶员模型,后续可进一步考虑人类驾驶员驾驶行为的不确定性、智能网联车辆渗透率、通信时延等因素,并分析其对车辆队列的影响。

