一种基于等步长分层拓展的混合A*路径规划方法
陈鑫鹏,徐 彪,胡满江,秦兆博,边有钢
(湖南大学 机械与运载工程学院,湖南 长沙 410082)
0 引言
智能车辆融合了先进传感器技术、高精度定位技术和先进决策控制技术,可有效提高车辆运行效率、提升驾驶安全性、减小驾驶员的驾驶负担,是当下汽车技术发展前沿[1]。路径规划作为智能车辆的核心技术之一,其主要任务是为车辆提供一条通往目的地的安全、无碰撞路径[2]。根据不同场景,智能车辆的路径规划可分为结构化道路的路径规划和非结构化道路的路径规划[3]。结构化道路(如高速公路、城市主干道等)包含明显的车道线、道路标识和车道边界等信息,可以直接为智能车辆提供参考路径,极大地降低了路径规划的复杂程度[4]。相较于结构化道路场景,非结构化道路场景(如矿场、港口、停车场和园区等)无车道线信息、地形场景开阔且道路边界复杂,因此,其智能车辆路径规划具有较大难度。目前,针对非结构化道路场景的路径规划方法主要分为基于采样的方法和基于图搜索的方法两大类。基于采样的方法主要包括PRM算法[5]、RRT算法[6]及其衍生算法[7-9],此类方法具有搜索速度快、不需要对环境进行具体建模等优点,但由于其随机采样的特性导致搜索的路径迂回曲折,难以得到稳定的最优或次优路径。基于图搜索的方法主要有Dijkstra算法、A*算法和D*算法等[10],采用此类方法搜索得到的路径虽能保证最优性,但难以满足车辆的运动学约束[11]。针对这一问题,Dolgov等人提出一种考虑车辆运动学性能的混合A*算法[12],通过对车辆前轮转角进行离散,拓展得到满足车辆运动学约束的子节点。但该方法采用的子节点拓展方式效率较低,且搜索得到的路径不够平滑,仍然难以满足智能车辆实际应用需求。对此,本文在传统混合A*算法基础上进行改进,提出一种新的子节点拓展方式,并对启发式函数(Heuristic)与代价函数进行合理设计,以提高其路径搜索效率与路径平滑性;同时对搜索得到的路径进行进一步平滑与插值,从而保证路径的最优性。
1 混合A*算法
传统A*算法可在栅格化的地图内进行路径搜索,首先建立一个open集和一个closed集,每搜索一步都利用评估函数f(s)=g(s)+h(s)(其中g(s)为代价函数,h(s)为启发式函数)对open集中的节点进行排序,并将评估代价最小的节点移到closed集中;然后以此节点作为父节点进行子节点拓展,从而构建出一棵搜索树。当终点加入搜索树后再通过路径回溯,即可获得一条从给定起点到达终点的最优路径,但由于其子节点只能朝父节点周围8个栅格中心拓展,故得到的路径无法给具有非完整约束的车辆执行。
混合A*算法沿用了传统A*算法的思想,与传统A*算法不同的是,其子节点位置是根据拓展步长、车辆最小转弯半径以及前轮转角离散数量而确定的,因此可以访问栅格中的任意位置,从而保证了最终搜索得到的路径能够满足车辆运动学要求。图1示出传统A*算法与混合A*算法子节点拓展示意。
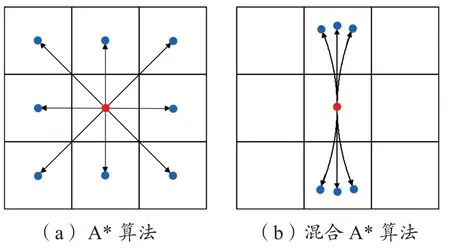
图1 A*算法与混合A*算法子节点拓展示意Fig.1 Node expansion diagram of A* and hybrid-A*algorithms
2 改进混合A*算法
传统混合A*算法采用等步长单层拓展方式,其搜索效果受前轮转角离散数量和搜索步长影响较大。前轮转角离散数量过大或搜索步长过小,都会降低搜索效率;前轮转角离散数量过小或搜索步长过大,则会降低路径的平滑性与安全性。为了同时保证算法搜索效率和路径平滑性,本文提出一种新的子节点拓展方式。其采用等步长分层拓展的方法,既能保证搜索得到的路径平滑性与安全性,又能大大提高路径搜索效率。同时,通过合理设计启发函数和代价函数,避免了节点沿着不必要的区域或方向进行拓展,进一步提高了路径搜索的实时性。
2.1 搜索空间表示
车辆在平面中的状态可表示为(x,y,φ,d),其中(x,y)表示车辆所处位置,φ表示航向角,d表示车辆行驶方向(d=0为前进,d=1为后退)。采用该种车辆状态表达方式即创造了一个复杂的四维搜索空间,必须对其进行离散才能使用混合A*算法进行路径搜索。具体计算方法为

式中:x——(x,y)连续车辆位置信息;——离散车辆位置信息;——离散车辆航向角信息;ξ——位置离散分辨率;γ——角度离散分辨率;o——选取的坐标原点。
2.2 子节点拓展方式
结合图2所示的车辆运动学自行车模型,本文所采用的子节点拓展方式具体步骤如下:
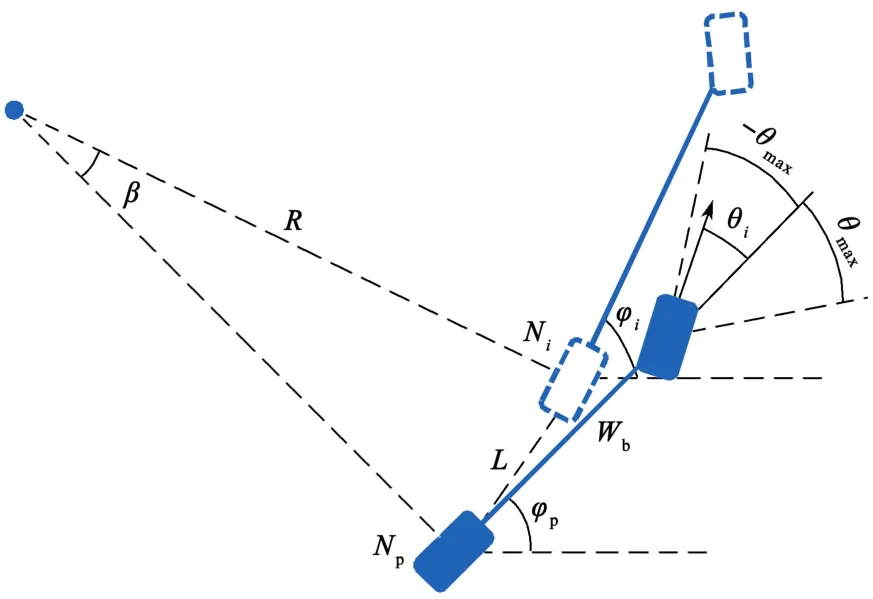
图2 车辆运动学模型Fig.2 Vehicle kinematics model
(1)确定前轮转角离散数量N。为了保证子节点能朝车辆直行方向拓展,N必须为奇数。将前轮转角范围[-θmax,θmax]进行均匀离散,得到每个离散位置的前轮转角为
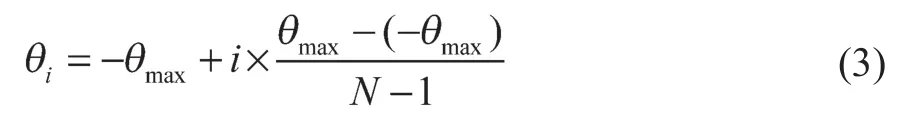
(2)确定从每个离散前轮转角处向前或向后拓展的子节点数量Mi。由于倒车行驶不符合人类驾驶习惯,故本文将向后拓展的节点数量Mi设置为1,保证每次向后拓展的距离较短;而对于向前拓展,为保证车辆尽可能地保持直行,故减少不必要的转弯,子节点数量Mi可由式(4)计算得到:
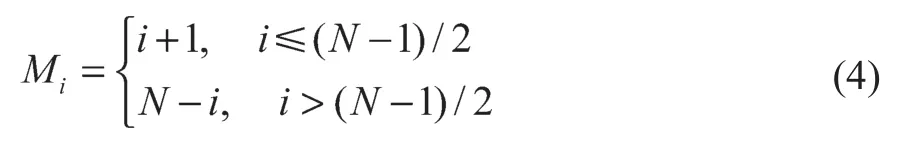
(3)与传统混合A*算法的单步拓展方式不同,改进混合A*算法从每个父节点Np(xp,yp,φp,dp)开始进行等步长分层拓展,各子节点Ni(xi,yi,φi,di)的计算公式如下:
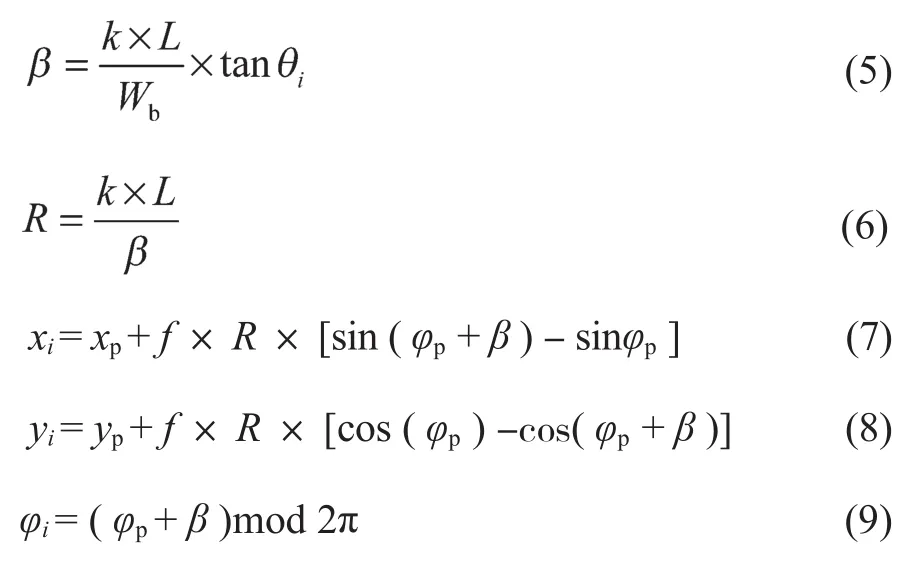

式中:k——拓展层数,k= 1, 2, …,M;f——正负号标志,向前拓展时f取1,向后拓展时f取-1。
(4)对拓展得到的每个车辆位姿进行碰撞检测,若车辆在该节点位姿处与障碍物碰撞,则停止在该前轮转角处继续向外层拓展节点,以保证各子节点与父节点之间的路径无碰撞。
图3示出选取N=7,9和11时的子节点拓展效果。由图可知,采用此子节点拓展方式既能完成长距离的直线探索,又能保证在必要位置进行不同程度的转弯。
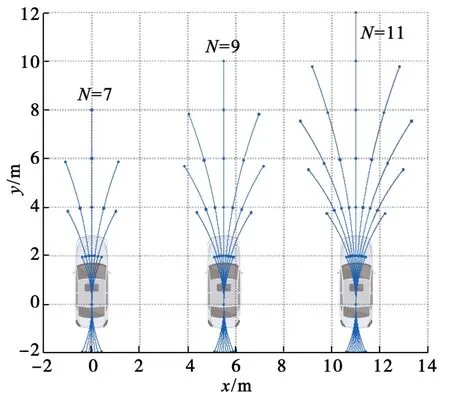
图3 节点拓展效果示意Fig.3 Schematic diagram of node expansion effect
2.3 启发式函数设计
启发式函数对于A*类算法至关重要,由启发式函数计算得到的启发值越接近实际值,路径搜索效率则越高。传统A*算法以欧式距离(即两点间直线距离)或曼哈顿距离(即两点在标准坐标系上的绝对轴距总和)作为启发式函数,由于忽略了障碍物约束,导致对实际路径成本估计不准确。本文采用Dijkstra算法以在二维障碍物地图中计算得到的每个栅格点与终点的距离作为启发值,如图4(b)所示,颜色越深,表明启发值越大,即离目标位置的距离越远,相较于图4(a)以欧式距离计算得到的启发值,其更加符合实际情况。
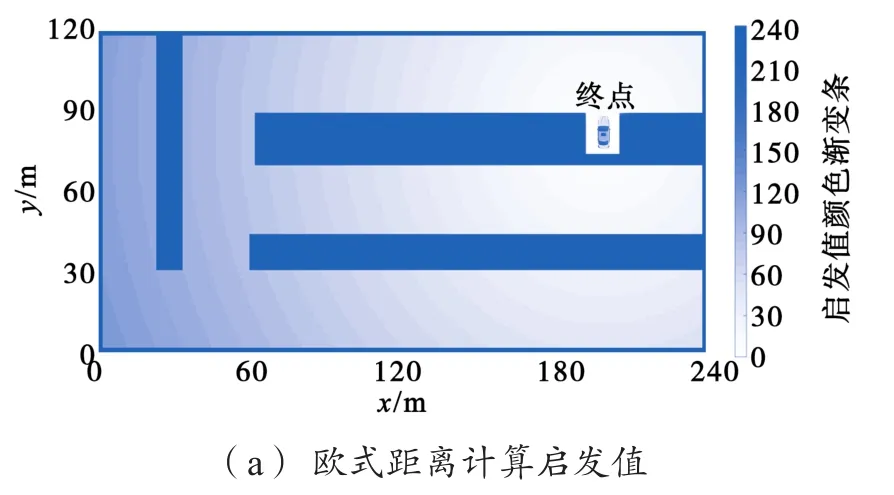
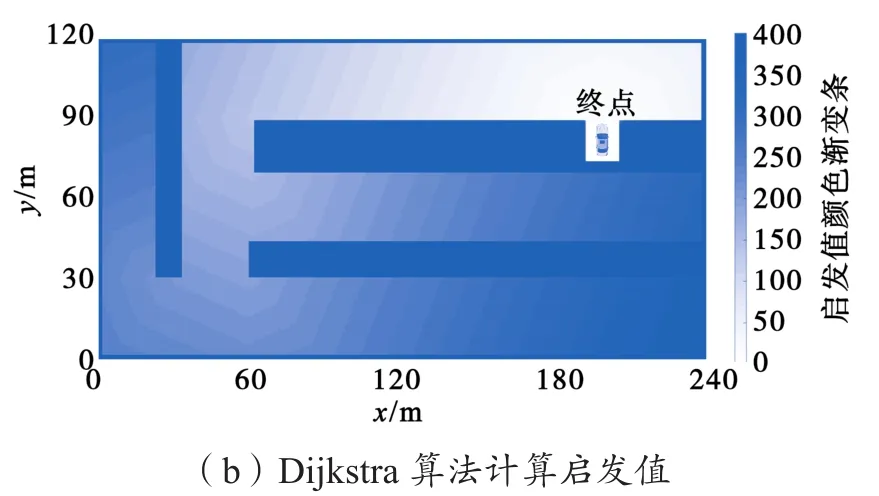
图4 不同启发函数对比Fig.4 Comparison of different heuristic functions
2.4 代价函数设计
为了使搜索得到的路径能让车辆尽可能地保持直行,减少不必要的转弯和后退,本文考虑在代价函数中加入对转弯和后退节点的惩罚,各子节点Ni(xi,yi,φi,di)的实际代价计算公式如下:
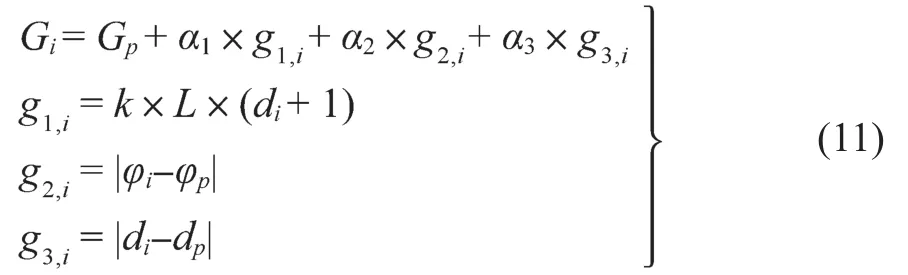
式中:Gp——父节点Np的代价;Gi——子节点Ni的代价;α1,α2,α3——权重系数,可通过多次试验后选取。
根据所设计的代价函数,通过g1,i对后退的搜索给予惩罚,并考虑了节点拓展时的步长代价,保证前向路径搜索的优先性;通过g2,i对路径点航向角改变给予惩罚,保证了路径平滑性;通过g3,i对路径点方向切换给予惩罚,能够有效避免路径出现频繁前进后退切换现象。
2.5 终点区域曲线拟合
由于采用2.2节所述的子节点拓展方式无法精确搜索到目标位姿,需要进行曲线拟合,故本文采用Reeds-Shepp曲线(简称“RS曲线”)[13]进行终点区域曲线拟合。如图5所示,当选择的待拓展节点距终点距离小于一定阈值时,以当前节点位姿作为起点位姿,使用RS曲线拟合到目标位姿;若拟合路径碰撞检测通过则停止搜索,否则继续进行子节点拓展。
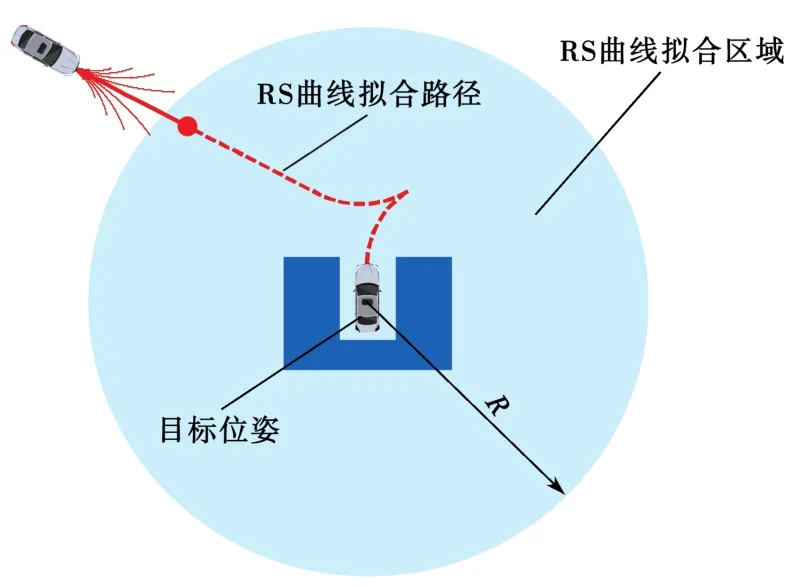
图5 RS曲线终点拟合示意Fig.5 Endpoint fitting diagram of RS curve
3 路径后处理方法
使用图搜索方法搜索得到的路径存在曲率不连续、包含不必要转弯和路点间距不均匀的问题,本文对其做进一步的平滑与插值。首先采用梯度下降法对搜索得到的路径进行非线性优化,以提高路径的平滑度,改善路径曲率连续性;然后采用三次样条曲线对优化后的路径做进一步的插值处理,得到稠密且均匀的路点,以满足实际车辆控制需求。
3.1 路径优化
设混合A*搜索得到的初始路点序列为xo,j=(xj,yj),j∈[1,N],优化的初始解为xj=xo,j。固定起始点和目标点,对中间各点采用梯度下降法进行优化,目标函数定义为
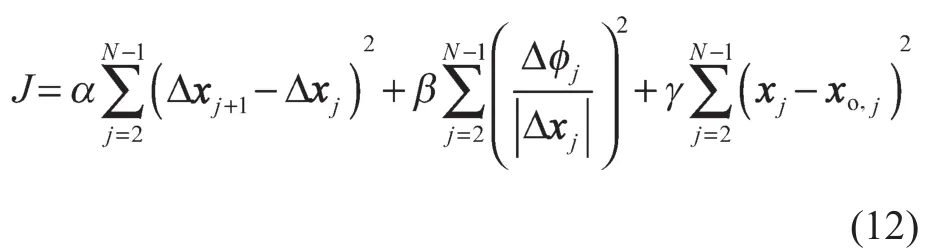
式中:Δxj——各路点之间的位移矢量,Δxj=xj-xj-1;——各路点之间切向角的变化量;α,β,γ——各项权重系数,可通过多次试验选取。
目标函数的三项分别考虑了路径平滑性、曲率约束和优化路径与原路径的偏离程度,各项梯度的求解可参考文献[12]。值得注意的是,采用本方法优化得到的路径可能会与障碍物发生碰撞。若出现这种情况,则参考初始路点xo,j,对优化后发生碰撞的路点进行固定,并再次进行优化处理,同时加大目标函数中的第三项权重系数,以减小优化后路径与原路径的偏差,直到路径碰撞检测通过后停止。
图6示出某非结构化道路场景下路径优化前后对比,图7示出为对应路径优化前后曲率对比。可以看到,优化后路径具备更好的平滑性和曲率连续性,满足车辆的实际行驶要求。
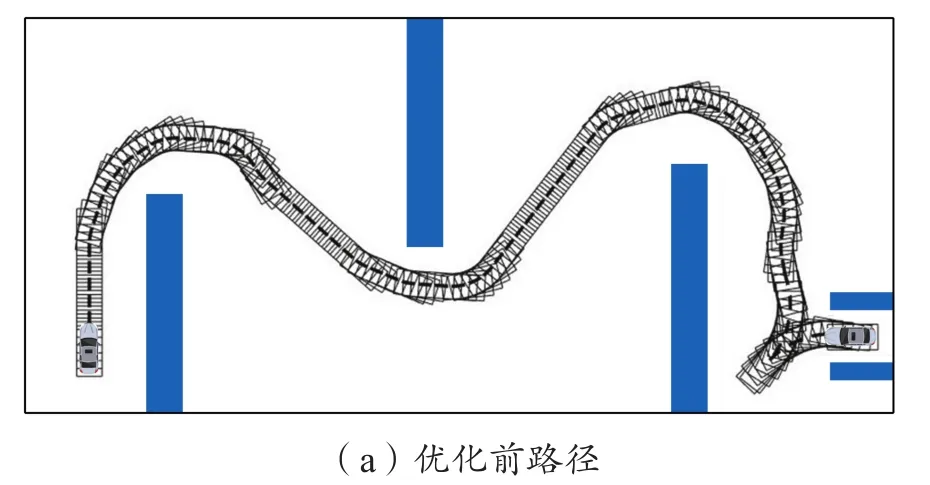
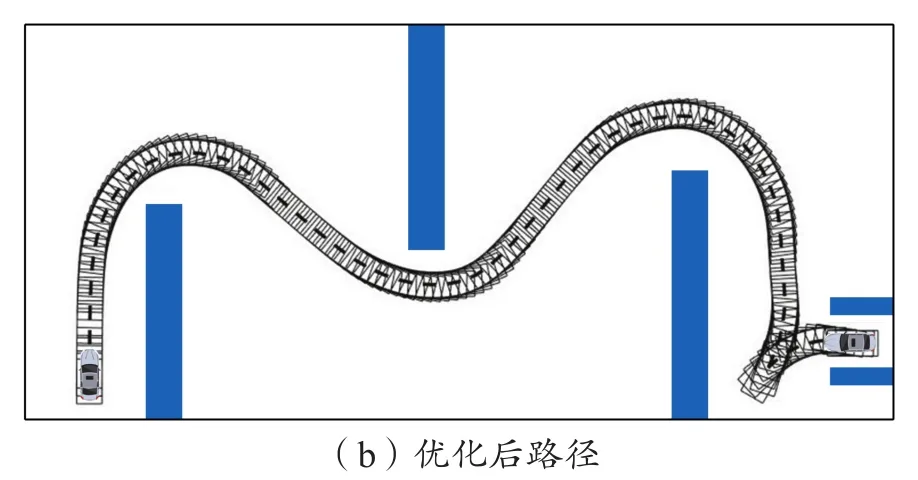
图6 优化前后路径对比Fig.6 Contrast of paths before and after optimization
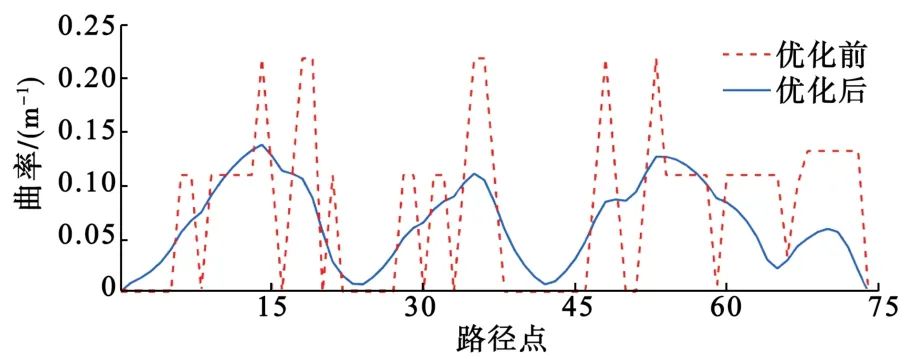
图7 优化前后曲率对比Fig.7 Contrast of curvatures before and after optimization
3.2 路径插值
为了使优化后的路点之间更加稠密,以满足车辆控制需求,本文采用三次样条曲线对路点进行插值。在此之前,由于路径优化过程导致搜索得到各路点航向角信息丢失,此时需要重新进行计算。如图8所示,保持起点、终点和其他固定点的角度不变,中间点xj则是以前后两点(xj-1和xj+1)连线方向与x轴正向的夹角作为该点的航向角φj。
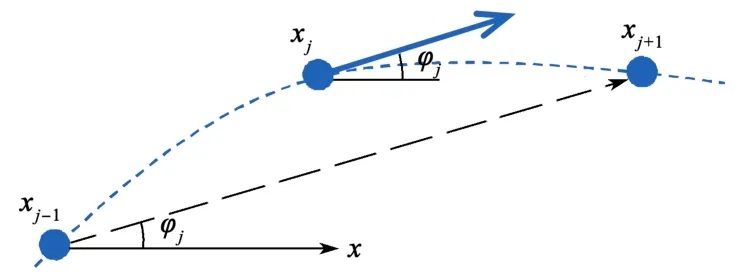
图8 路点航向角计算示意Fig.8 Diagram of road point heading angle calculation
得到路点航向角信息后,再结合每个路点的坐标信息,即可求得每两个路点之间插值用三次样条曲线的各项系数,继而得到各路点之间的插值点坐标,具体求解方式可参考文献[4]。插值前后路径对比如图9所示。
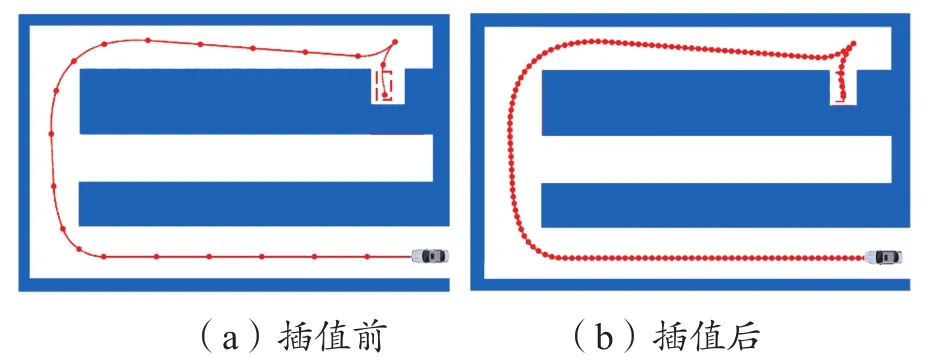
图9 插值前后路径对比Fig.9 Comparison of paths before and after interpolation
4 试验验证
通过仿真和实车试验,验证本文所提等步长分层拓展混合A*算法的有效性和实用性。首先,基于Matlab平台搭建了若干个仿真场景,对本文所提方法与传统混合A*算法进行了对比试验,以验证算法的优越性。然后,基于机器人操作系统(robot operating system, ROS)进行C++算法开发,通过实车采集停车场地图,得到实际的非结构化道路场景。在该场景下进行实车路径规划试验,进一步验证本文所提方法的可靠性。试验相关参数见表1。

表1 试验相关参数Tab.1 Related parameters of the experiment
4.1 仿真对比试验
如图10所示,在80 m×40 m的仿真地图中对本文提出方法与传统混合A*算法进行仿真对比试验,试验结果数据如表2所示。可以看出,本文方法相较于传统混合A*算法可有效减少拓展节点数量,同时,closed集中存放的节点数量降低了一个数量级。根据A*算法原理可知,采用本文方法进行路径搜索时的循环次数也降低了一个数量级,从而大大提高了路径搜索效率,使算法具备更好的实时性。
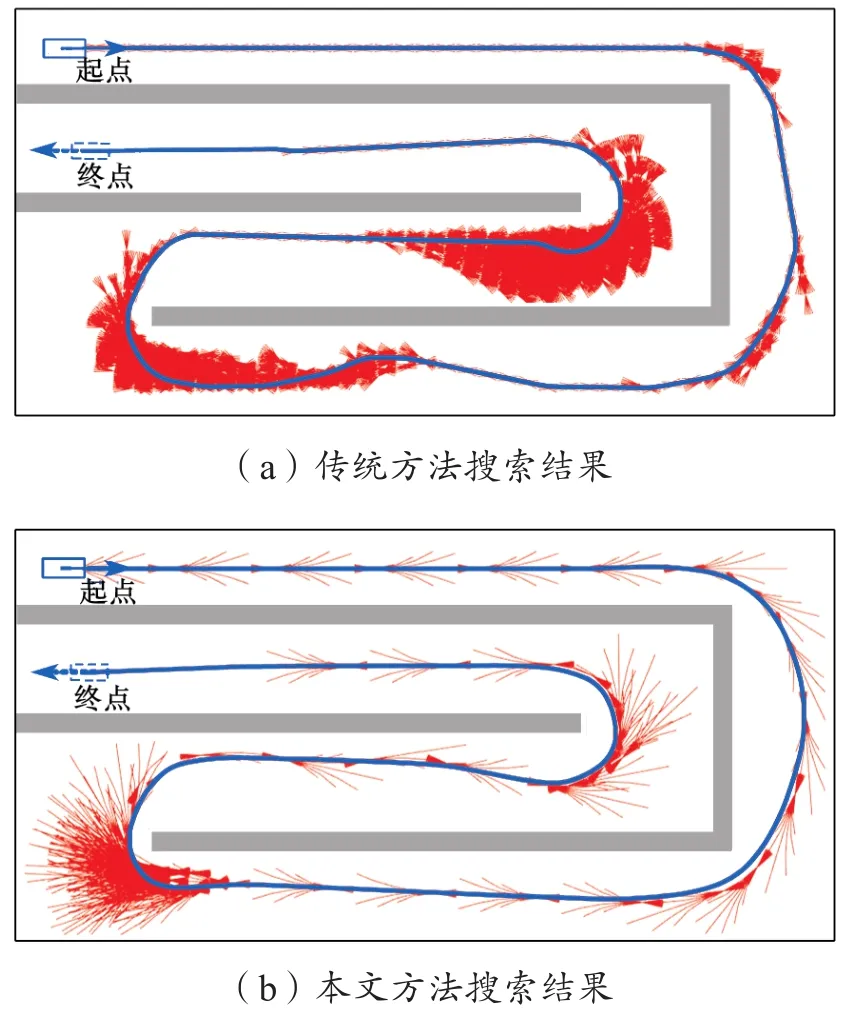
图10 路径搜索结果对比Fig.10 Comparison of the path search results
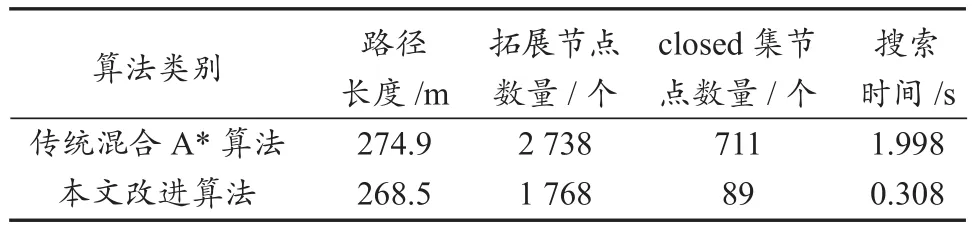
表2 仿真试验数据对比Tab.2 Comparison of simulation experiment data
由表2可知,采用本文所提改进算法较传统混合A*算法,路径搜索时间缩短了84.6 %。此外,除了图10所示的试验场景,本文还针对其他不同的场景进行了仿真对比试验,试验结果显示平均路径搜索时间缩短了51.6%,进一步验证了该方法相较于传统混合A*算法的优越性。
4.2 实车试验
为了进一步验证所提出方法的可靠性,本文针对实际的非结构化道路场景进行了实车试验。如图11所示,本实验所使用的试验车辆为改造的乘用轿车,配备有激光雷达、毫米波雷达以及惯导等感知和定位设备。图12(a)为测试的实际停车场场景(大小约为100 m×30 m),在该地图场景中设置终点进行路径规划。图12(c)为搜索得到的初始路径,总拓展节点数量为551个;图12(d)为优化后的最终路径,采用Intel i5-8300H型处理器进行计算,得到的路径搜索与优化总用时为37 ms。试验结果表明,本文所提方法能够在非结构化道路场景中以较短时间搜索得到一条安全、平滑且满足车辆运动学约束的车辆可行驶路径。
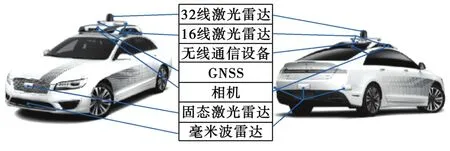
图11 试验车辆Fig.11 Test vehicle
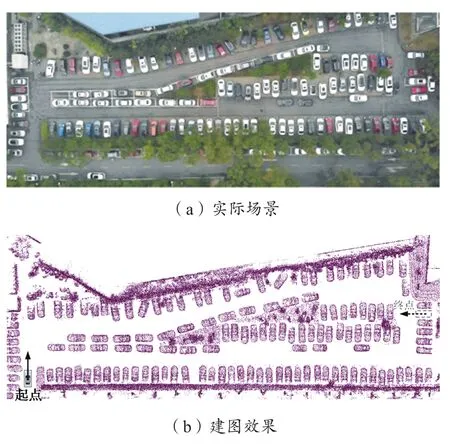
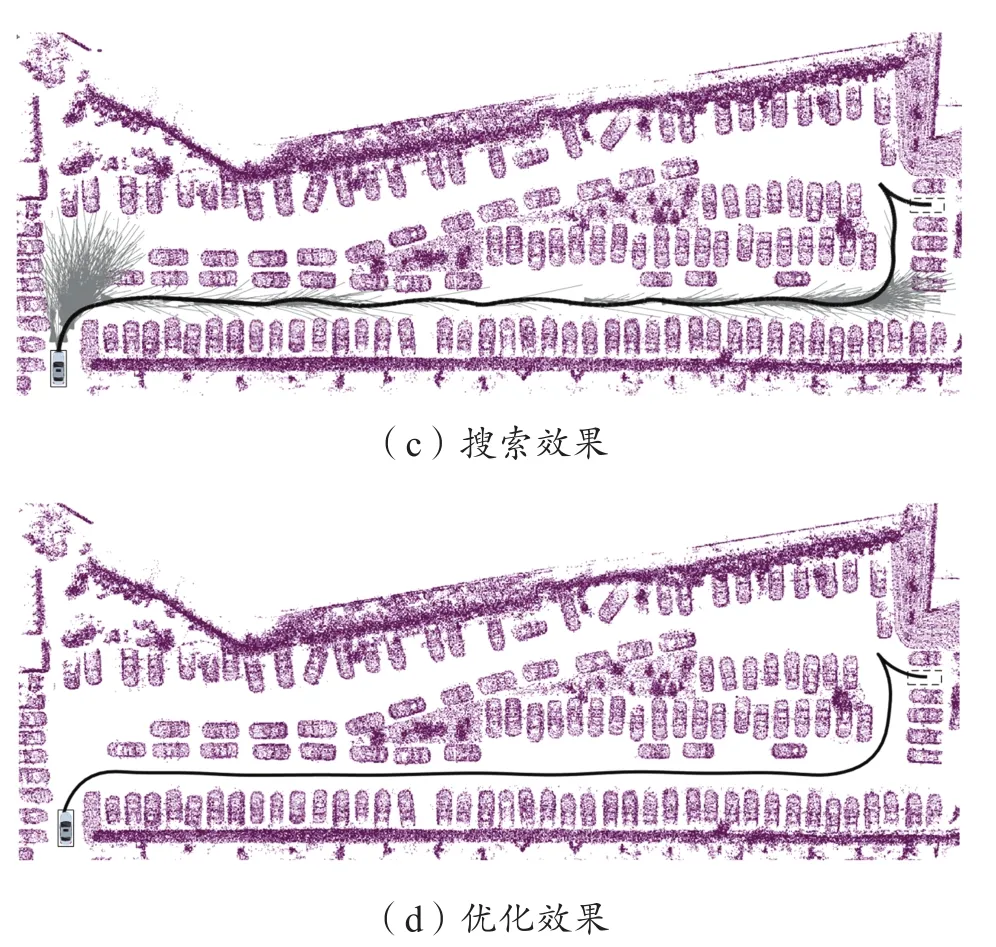
图12 实际场景实车试验验证Fig.12 Actual scene of experiment verification
5 结语
本文对非结构化道路智能车辆的路径规划方法进行了研究,提出了一种基于等步长分层拓展的混合A*路径规划方法。首先,通过改进传统混合A*算法的子节点拓展方式,保证路径安全性的同时提高了节点拓展效率;通过合理设计启发式函数与代价函数,进一步减少了不必要的节点拓展。然后,采用梯度下降法对搜索得到路径进行优化处理,得到一条平滑舒适的车辆可行驶路径。最后利用三次样条曲线对稀疏路径点进行插值,得到稠密且均匀的路点,以满足实际车辆控制需求。仿真对比试验和实车试验结果表明,本文所提出的方法能显著提高传统A*搜索算法的搜索效率,同时保证了最终生成路径的安全性、平滑性以及车辆的可行驶性。本文主要解决了非结构化道路场景下的智能车辆路径规划问题,但未对车辆沿路径行驶时的速度进行规划,因此,后续将对非结构化道路场景下的智能车辆速度规划方法展开研究。

