激光偏振散射法测量钢化玻璃应力的分析

武文杰 张哲 黄达泉 苑静

（北京奥博泰科技有限公司 北京 100070）

0 引言

钢化玻璃是一种有预应力的玻璃，具有强度高、承载能力大、抗冲击性强等优点［1］，现已经广泛应用于建筑玻璃、防火玻璃、汽车机车、航空玻璃、太阳能光伏光热玻璃等各个领域，物理钢化玻璃的制备原理是将玻璃加热到600～700 ℃（接近玻璃软化点）的温度，然后再使之迅速冷却，最终在玻璃表面形成压应力层，而玻璃中部是拉应力层［2］，这样的应力是由于温度梯度的作用而引起的力学不均匀和结构不均匀导致的。化学钢化玻璃的制备原理是通过离子交换的方式，实现玻璃中的碱金属离子与熔盐中的金属离子的交换，从而在玻璃表面形成压应力层，在玻璃中部形成张应力层［3］。表面应力是衡量钢化玻璃抗冲击性、稳定性、安全性等特性的重要指标，GB 15763.2规定钢化玻璃的表面应力不小于90 MPa［4］。玻璃内部两个零应力层之间的厚度越宽，中部张应力峰值就越低，杂质（主要为硫化镍）引起玻璃自爆的风险越小，玻璃安全性越高［5］，对玻璃厚度方向应力分布的测量，是分析零应力层位置的有力手段，可以用于判断玻璃安全性能等级，有利于排除玻璃自爆的安全隐患。所以为确保钢化玻璃达到各种情况的加工及使用要求，需要对钢化玻璃的表面应力和板厚方向应力分布进行准确地测量。

由于钢化玻璃是不可裁切的，所以传统的加载法、盲孔法等破坏性的应力测量方法并不适用于钢化玻璃。光波导法可测量钢化玻璃的表面应力，但是该方法是利用浮法玻璃表面锡扩散层的光波导效应对表面应力进行测量，只能从锡面测量表面应力，不适用于浮法玻璃的空气面和没有锡面的钢化玻璃，也不适用于当中空玻璃、夹胶玻璃等玻璃成品与已安装钢化玻璃的锡面在无法测量的位置时的情况，更无法测量玻璃板厚方向的应力分布。Weller［6］在1939年提出的散光法在兼具表面应力测量的同时还解决了玻璃板厚方向应力分布的测量问题，该方法能适用于浮法玻璃的锡面、空气面和非浮法工艺生产的玻璃，也可以测量玻璃的锡面位于不便测量位置情况下的钢化玻璃成品及已安装的钢化玻璃（如：锡面位于腔体内的中空玻璃、锡面位于夹胶层的夹胶玻璃等）的应力。

经过几十年的发展，散光法已经以激光为光源（以下称“激光偏振散射法”），并逐渐发展成熟，与计算机图像处理技术相结合，可方便快捷地测量应力，但目前关于激光偏振散射法的资料较少，并且很少有资料系统的给出完整的方法推导，国内外的相关标准也一直处于空白状态。

本文介绍了激光偏振散射法的详细原理，在散射干涉条纹处理方面给出了基于数字图像处理技术的四步移相法，并用四点弯曲试验对该方法的准确性进行了验证。

1 激光偏振散射法的原理

激光偏振散射法有正射法与斜射法之分，二者基本原理相同，本文以斜射法进行讨论。

通常情况下，玻璃是各向同性体，各个方向的折射率都相同，而钢化玻璃是一种有预应力的玻璃，应力的存在会破坏这种各向同性性质，使两主应力方向的折射率不再相同，产生应力双折射现象［7］。

假设入射偏振光振动方程为E0＝Acoswt，A为入射光振幅。如图1所示，光束以i的入射角倾斜入射进玻璃，O点为光线传播路径上传播距离为s的一点，sx（ s）与sy（s）是与入射方向相垂直的平面内的两正应力，散射光探测方向为OL，入射光偏振方向是OP，q为sx（s）与OL之间的夹角，b为sx（s）与OP之间的夹角。

图1 光束传播路径上各点的偏振方向、探测方向的相对位置

由于应力双折射现象，光线在O点可以沿sx（s）与sy（s）分解为振动方向相互垂直的两束偏振光Ex（ s）与Ey（s），如图2所示。

图2 光束在传播路径上各点的分解

两束光的位相差为d（s），振动方程式为：

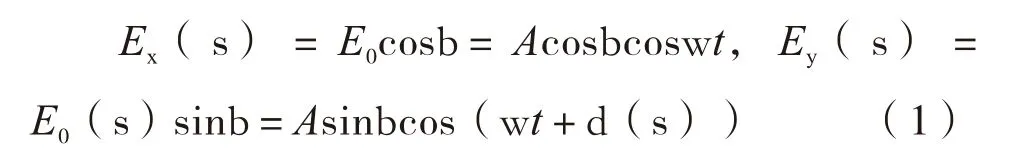
在OL方向可观测到振动方向与OL相垂直的光矢量，将Ex与 Ey投影到与OL相垂直的方向，投影后的E'x（s）与E'y（s）为：

在OL方向观测到的合成光波EL（s）为：

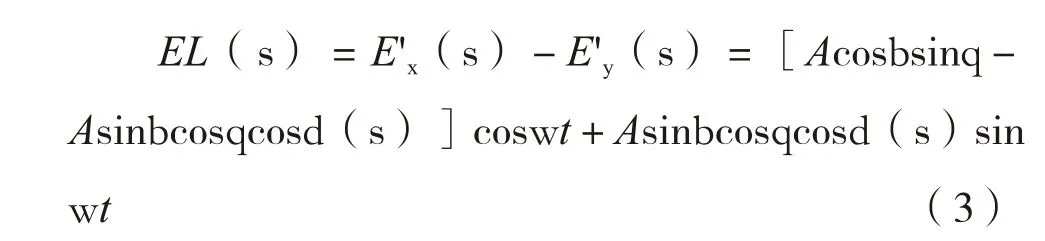
合成光波EL（s）是随光线传播路径变化的椭圆偏振光，可用式（4）表示：

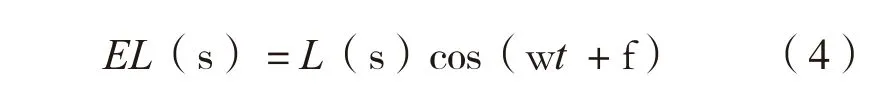
式中：L（s）——合成光波的振幅。

由式（3）与式（4）可得到在OL方向观测到的光矢量的振幅L（s），表达式为：

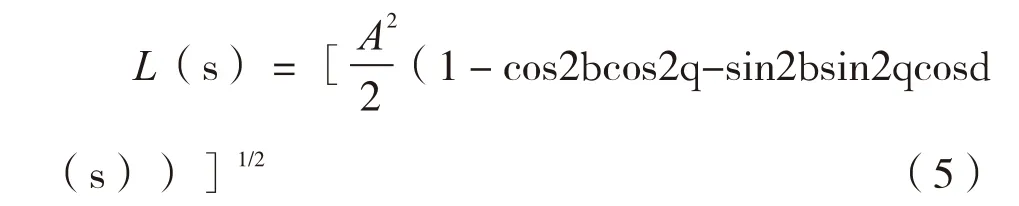
考虑到玻璃材料对光线的散射，最终可获得在OL方向观测到光矢量的光强I（s）：

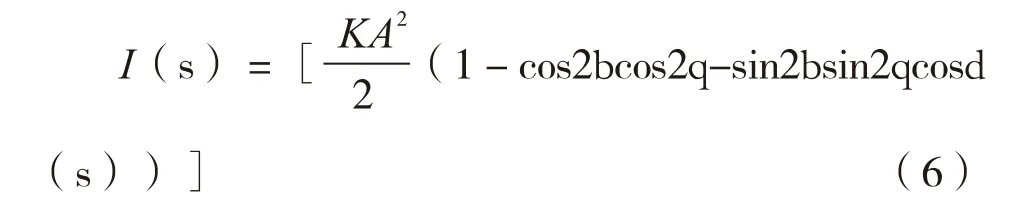
式中：K——与材料的散光性能有关的常数。

当试验装置制作完成后，b 与q 也就随之确定不变，由式（6）可以看出，光强I 随着相位差d（s）的变化而变化，也就是说在OL方向可以观察到明暗相间的散射干涉条纹。当b＝q＝45°时，I（s）的最小值为0，最大值为（KA2）/2，此时光线传播路径上各点的光强的对比度最好。

根据应力光学定律，光线传播路径上各点的应力s（s）与位相差d（s）有式（7）的关系，值得注意的是各点应力的大小与该点位相差的大小无关，只与该点位相差随路径的变化率有关：

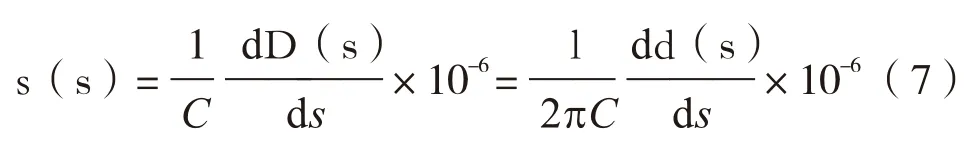
式中：C——被测玻璃应力光学常数，MPa-1，钠钙硅玻璃的应力光学常数取2.60×10-6MPa-1，硼硅玻璃的应力光学常数取3.90×10-6MPa-1；

D（s）——Ex（ s），Ey（s）两光束的光程差，nm。

式（7）给出了应力、光程差、位相差的关系，求得光程差或位相差即可求得应力。在激光偏振散射法发明后的很长一段时间内，技术人员都是利用补偿法，根据光程差与散射条纹之间的关系求应力的，但这种方法的误差，特别是人为引入的误差较大。随着计算机科学技术的发展，基于数字图像处理的自动化测试方法面世并得到了极大的发展，该方法测量精度更高，可在很大程度上减少人为误差的引入，本文着重介绍基于数字图像处理技术的四步相移法。

未施加初始位相时光线在传播路径上各点的沿应力方向分解的两个偏振光分量位相差主值d'（s）与施加不同初始位相时的光线传播路径上各点散射光光强I1（s）、I2（s）、I3（s）、I4（s）的关系为：

反正切函数的值域是［－p/2，p/2］，所以由式（9）求得的d'（s）是相位差的主值或者是包裹相位差，必须通过相位去包裹算法将各点沿应力方向分解的两个偏振光分量的位相差主值d'（s）转换为沿应力方向分解的两个偏振光分量的位相差d（s）。相位去包裹算法在光学检测领域应用广泛，是分析干涉条纹的有力手段，经过多年的发展，已有多种较成熟的算法［9,10］，这里不再赘述。将d（s）代入式（7）即可获得光线传播路径上各点的应力值，最终得到如图3所示的板厚方向应力分布曲线。由图3可获得被测玻璃的表面应力与板厚方向的应力分布。当然，除了四步相移法之外，还可以采用其他步数相移法，只要相移步数不小于3即可。

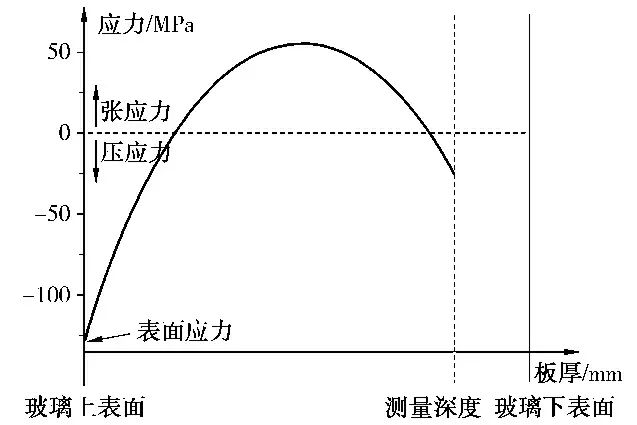
图3 板厚方向应力分布曲线

2 激光偏振散射法测量准确性的核验

国内外通常用四点弯曲试验对激光偏振散射法的测量准确性进行核验，试验在温度为23℃±5℃、相对湿度为25%～75%的环境中进行。本文中的四点弯曲试验是按照ASTM 1377的规定设置的。

2.1 激光偏振散射法的应力仪

选择GlasStress SCALP应力分析仪（以下简称“SCALP应力仪”）作为核验用仪器，该仪器符合本文中关于激光偏振散射法的各项描述，一般包括激光光源、起偏器、电控相移器、耦合棱镜、调节与控制装置、数字面阵相机、信号采集与处理单元等。仪器结构示意见图4。

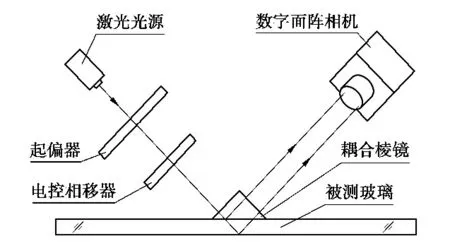
图4 SCALP应力仪结构示意图

2.2 核验过程与结果

四点弯曲试验原理如图5所示。

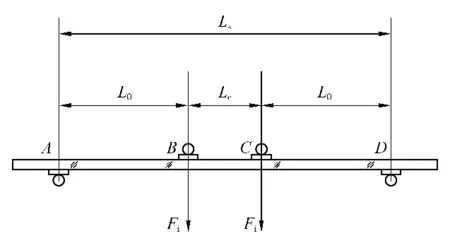
图5 四点弯曲试验原理示意图

B、C是两加载位置，A、D是两支承位置，B、C之间的距离（Lc）为3w，相邻支承与负载之间的距离Lo≮4w。四点弯曲试验应力计算公式为：

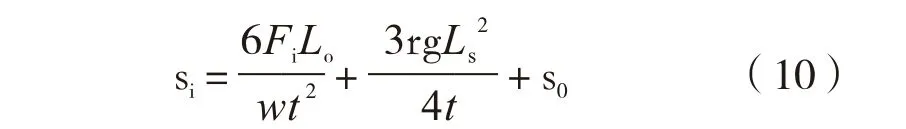
式中：si——施加第i个加载力后，样品BC中点的表面应力，MPa；

s0——样品被测点的残余应力，MPa，应使用在校准有效期内的应力仪测量获得；

Fi——第i 个加载力，N；

t——样品厚度，mm；

w——样品宽度，mm，8 t≤w≤12 t；

Lo——相邻支承与负载之间的距离，mm；

r——样品密度，kg/mm3，对于普通钠钙硅玻璃 r＝2.5×10-6kg/mm3；

g——重力加速度，N/kg，一般取9.8 N/kg；

Ls——两支承之间的距离，mm。

选择退火良好的厚度为5 mm、6 mm、8 mm、10 mm的浮法白玻作为被测样品，分别记为1#、2#、 3#、 4#，被测样品需在温度为23℃±5℃、相对湿度为25%～75%的环境中放置2 h以上。试验前根据各样品的最大断裂应力，通过式（10）估算加载位置可施加的最大力，确保施加的力不会使样品发生断裂，在两加载位置施加10个递增的力Fi（ i＝1、2、3……10），Fi包括四点弯曲试验加载装置的重力和加载砝码的重力，根据式（10）计算施加不同加载力后样品BC中点表面应力，作为理论值，使用SCALP应力仪沿宽度方向测量3次不同加载力时BC中点的表面应力，3次测量的平均值作为测量值。偏差为每个加载力下SCALP仪器测量值与理论值的差值，核验数据如表1所示，不同样品的加载力不同。

表1 利用四点弯曲试验对仪器进行核验的测量结果 MPa

由表1测试数据可知：每个加载力下，通过激光偏振散射法应力仪测得的各样品表面应力测量值与理论值都有一定的偏差且都是负值，可能的原因是四点弯曲理论计算公式适用于样品挠度较小的情况，而按照ASTM 1377的规定进行试验时，样品存在较大挠度，理论计算的表面应力与实际表面应力存在系统偏差。综合来看，每个加载力下每个样品的偏差都在±5 MPa之内，激光偏振散射法测值与四点弯曲试验理论值的差值较小，可满足测试要求。

3 结论

采用破坏性的应力测量方法并不适用于钢化玻璃，业内普遍使用的光波导法只能在浮法玻璃的锡面进行表面应力的测量，也无法测量板厚方向的应力分布。激光偏振散射法没有上述限制，可测量各种玻璃的表面应力及板厚方向的应力分布，适用于钢化玻璃的应力测量。通过激光偏振散射法获得的应力与四点弯曲试验理论应力的偏差较小，可满足测试要求。