高速列车用6008铝合金动态变形本构与损伤模型参数研究*
高玉龙,孙晓红
(中车青岛四方机车车辆股份有限公司,山东 青岛266111)
高速列车在国民经济和生产生活中扮演着愈来愈重要的角色。随着列车速度逐步提升,列车运行安全性(如碰撞脱轨、强侧风)已经成为人们重点关注的工程科学问题[1-2]。在高速碰撞过程中,车体材料和结构会经受强动载荷,因此开展车体材料和结构的耐撞性研究势在必行[3-4]。由于整车碰撞实验成本高昂,现场测试困难,大型数值模拟平台是研究列车碰撞问题的重要工具[5-7]。
车用材料在服役过程中会经受复杂的应力状态和严苛的环境条件(如高应变率、高低温)[2]。目前列车碰撞模拟大都将车体简化为刚体[5,7],很少考虑车体材料和结构的弹塑性变形和损伤断裂演化过程,这与真实工况有较大差异[8],不利于开展精确的列车安全性评估。因此研究考虑应变率效应和变形损伤效应的材料动态本构和损伤模型对开展精确的列车碰撞模拟和人车安全性评估至关重要[9]。
Johnson-Cook (J-C)模型是目前应用最广泛的材料本构模型,由Johnson 和Cook 于1983年提出[10]。J-C模型是一种研究得比较成熟的模型,它将材料加工硬化效应、应变率效应和温度效应解耦,因此,方程形式比较简单,便于工程应用。J-C模型已内置在很多大型商业有限元软件(如Abaqus)中,在材料加工、汽车耐撞性检验、高铁安全性测试、鸟撞飞机模拟等领域中得到了广泛应用[7-8,11-12],为工程结构设计提供了宝贵的技术参数和机理信息。但是,数值模拟的预测能力很大程度上依耐于模型参数的准确性,因此必须对材料J-C模型参数进行细致地实验标定。目前已发表的大多数文献和技术资料都集中在J-C本构模型的参数获取和验证上[11,13-14],而对J-C损伤断裂模型研究较少[15]。主要原因是J-C损伤模型的参数获取过程更为复杂,需要开展不同应力三轴度、不同应变率和不同温度的实验,还需要对试样的局部断裂应变进行精确测量。因此J-C损伤模型的参数获取还需开展大量研究工作。
6008-T4铝合金型材广泛用于新型高速列车的吸能结构[7,16],其防撞性能对高速列车的安全运行非常重要,但关于6008-T4铝合金冲击力学性能以及其J-C模型参数获取的研究还未见报道。本文基于上述背景,对6008-T4铝合金进行了多种力学性能测试,提出一种新的获取损伤模型参数的实验方法,进而标定和获取J-C本构和损伤模型参数;最后利用平板侵彻实验对所获取的参数进行检验,将模拟结果与实验结果进行比较,验证本文所获取的材料参数和参数标定方法的有效性,以期为J-C模型参数标定提供范式。
1 实验相关
1.1 Johnson-Cook 本构模型

1.2 Johnson-Cook 损伤断裂模型
J-C模型自带损伤断裂准则,其损伤断裂模型表达式为
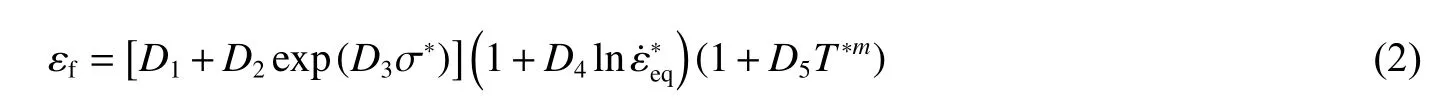
式中:σ*=σH/σeq表示应力三轴度,σH表示平均应力,σeq表示Mises等效应力;参数D1、D2、D3为描述应力路径对材料断裂应变影响的参数,参数D4和D5分别为表征应变率和温度对材料断裂特性影响的应变率敏感指数和温度敏感指数。式(2)等号右边三个因式分别代表应力三轴度、应变率和温度对材料断裂应变εf的影响。由于不同应力路径下试样内应变状态也不同,本文中断裂应变统一采用等效塑性应变来量度。
参数D4和D5的标定过程比较常规,但针对D1、D2、D3的标定过程,文献中则存在一些争议。本文将实验和数值模拟相结合,提出了一种的新的参数标定方法。其特点在于通过设计异形试样来改变加载路径即应力三轴度,分别为0°剪切(0)、45°剪切(0.197)、单轴拉伸(0.333)、单缺口拉伸(0.395)和双缺口拉伸(0.515),从而获取材料断裂应变与应力三轴度的变化关系,括号中为上述实验的理论三轴度[17]。上述实验可全部在拉伸试验机上完成。需要注意的是,J-C损伤模型中第一个因式的断裂应变是绝对值,因此参数标定必须采用局部断裂应变。例如,单轴拉伸实验中应力应变曲线显示的表观断裂应变要远远小于颈缩区的局部断裂应变,不能用于标定参数D1、D2、D3。0°和45°剪切实验以及单双缺口实验中只能获得力-位移曲线。因此,5 类实验中试样局部断裂应变都需要结合有限元模拟来求解,具体过程会在2.2节叙述。而J-C损伤模型中第2和第3个因式都是归一化应变,只要求断裂应变是在同一标准下获取即可,而无需真实的局部应变,下文针对D4和D5的标定过程全部采用真实应力应变曲线显示的表观断裂应变。
1.3 实验材料和样品
图2是标定过程中涉及的8种实验试样的形状和尺寸图。试样尺寸和加工精度都遵照国标GB/T228-2010《金属材料室温拉伸试验方法》。本文中准静态拉压实验均采用三思UTM5105试验完成。动态拉伸和压缩实验分别采用分离式霍普金森拉杆[19]和压杆[20]完成。所有实验结果都重复3次,然后取平均值。

图1 初始材料的EBSD 取向成像图Fig.1 EBSD inverse pole figure maps of initial materials
2 实验结果与讨论
2.1 弹塑性变形
图3是6008-T4铝合金准静态(0.001 s−1)单轴拉压下真实应力应变曲线的对比。压缩应力应变曲线的弹性段已根据材料的拉伸弹性模量(实测71.4 GPa)进行修正。从图中可以看出,拉伸和压缩曲线的屈服点(屈服应力144 MPa)和塑性段吻合很好,但单轴拉伸时试样的总塑性变形远小于单轴压缩时。
前人的文献在对J-C本构模型(式(1))中的参数B 和n进行拟合时,有些[15]采用单轴拉伸曲线,有些[14]则采用单轴压缩曲线,图4对比了两者的拟合效果。图中显示利用单轴拉伸数据拟合得到的参数B=(261±1.2)MPa,n=0.55±0.001 5;而利用单轴压缩数据拟合得到的参数B=(101±0.05)MPa,n=0.19±0.0005。虽然利用拉伸数据的拟合效果更好,但是这些参数只适用于材料塑性变形低于15%的情况。如果将参数延伸至大变形情况,可能会导致模型预测的硬化率和应力虚高。利用压缩数据拟合获得的参数B 和n可能在材料塑性变形较小的情况下产生预测偏差,但是当塑性应变较大时,利用压缩数据拟合获得的参数B 和n能够较好地预测材料的硬化率和应力。因此,在具体工程应用中,应该根据实际工况合理选择模型参数。

图2 试样形貌和尺寸(单位:mm)Fig.2 Configurationsand sizes of thesamples (unit:mm)
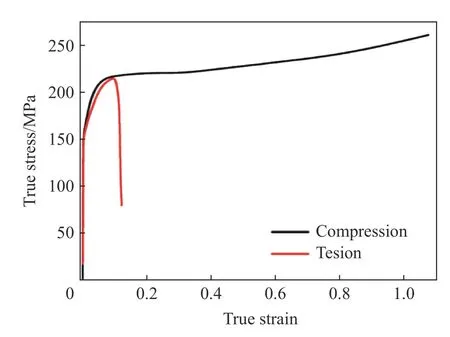
图3 铝合金单轴拉伸和压缩真实应力应变曲线Fig.3 True stress-strain curves of the aluminum alloys under uniaxial tension and compression
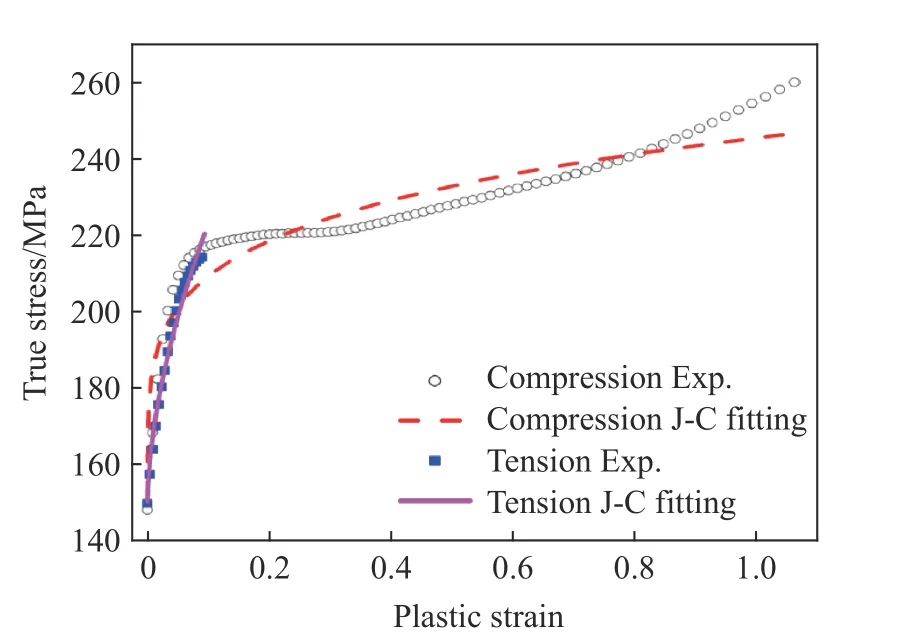
图4 J-C模型拟合曲线Fig.4 J-Cfitting to experimental curves
2.2 应力三轴度的影响
应力三轴度对材料的损伤断裂行为有显著影响[17]。为研究应力三轴度的影响,本文在室温准静态加载下开展了5类实验,即0°剪切、45°剪切、单轴拉伸、单缺口拉伸和双缺口拉伸;借助有限元模拟和已经标定好的J-C本构参数(A、B和n)结合实验中获取的力-位移曲线来计算试样的局部断裂应变。相比直接实验测量而言,实验和模拟结合的方法操作更加简便,精度也较高。
图5给出了利用Abaqus有限元软件模拟的室温准静态下0°和45°剪切实验中试样内塑性应变场的演化过程。图中显示0°剪切实验中试样内会逐渐演化出沿着拉伸方向的应变集中带,进而导致试样沿着0°方向发生剪切破坏。而45°剪切实验中试样则会在沿着45°方向形成应变集中带,进而发生45°方向的剪切破坏。
下面重点介绍如何利用模拟结合实验来计算5 类实验的局部断裂应变。因为文章篇幅有限,而且方法和结果类似,只以室温准静态下0°剪切实验和单缺口拉伸实验为例来说明上述方法并展示相应结果。方法如下:首先基于Abaqus有限元软件建立材料的弹塑性模型,利用2.1节中标定好的本构模型参数A、B 和n(压缩)模拟室温准静态下的0°剪切和单缺口拉伸实验;然后将模拟中获取的力-位移曲线与实验曲线进行对比,如图6)所示,其中叉状标记为试样断裂点。从图中可以看出,模拟和实验结果吻合很好,说明模拟试样中的应力应变状态和实验可以比拟。因为模拟中没有引入断裂准则,所以只能根据实验曲线确定试样的断裂点。由于宏观加载始终处于准静态状态,材料断裂产生的应力释放效应对材料局部应变影响较小(变形需要时间),因此模拟中没有考虑断裂过程并不会影响损伤模型参数的标定。
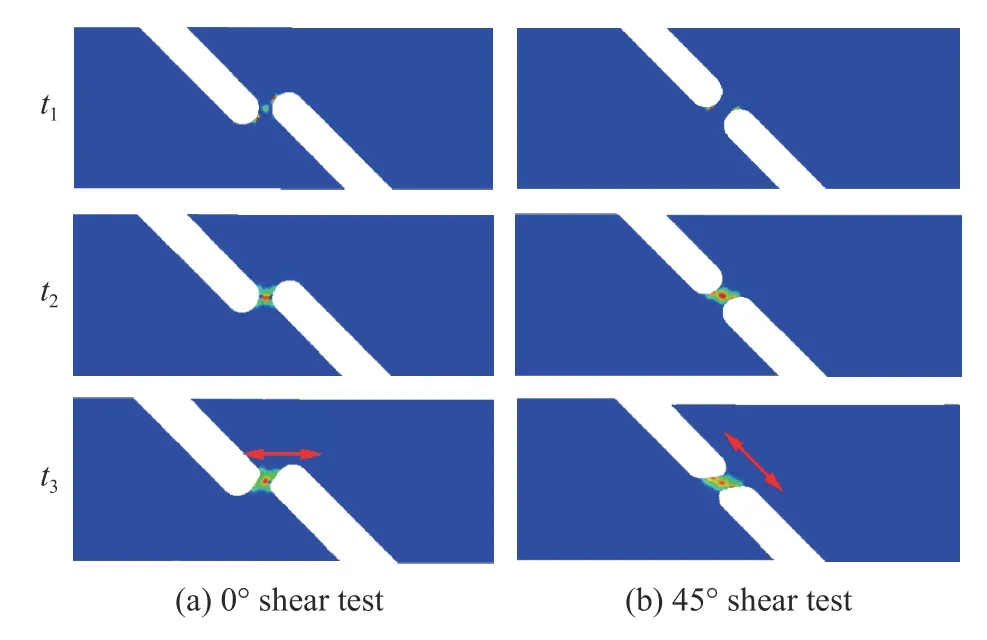
图5 模拟塑性变形场演化过程Fig.5 Evolution of simulated plastic strain fields in the samples
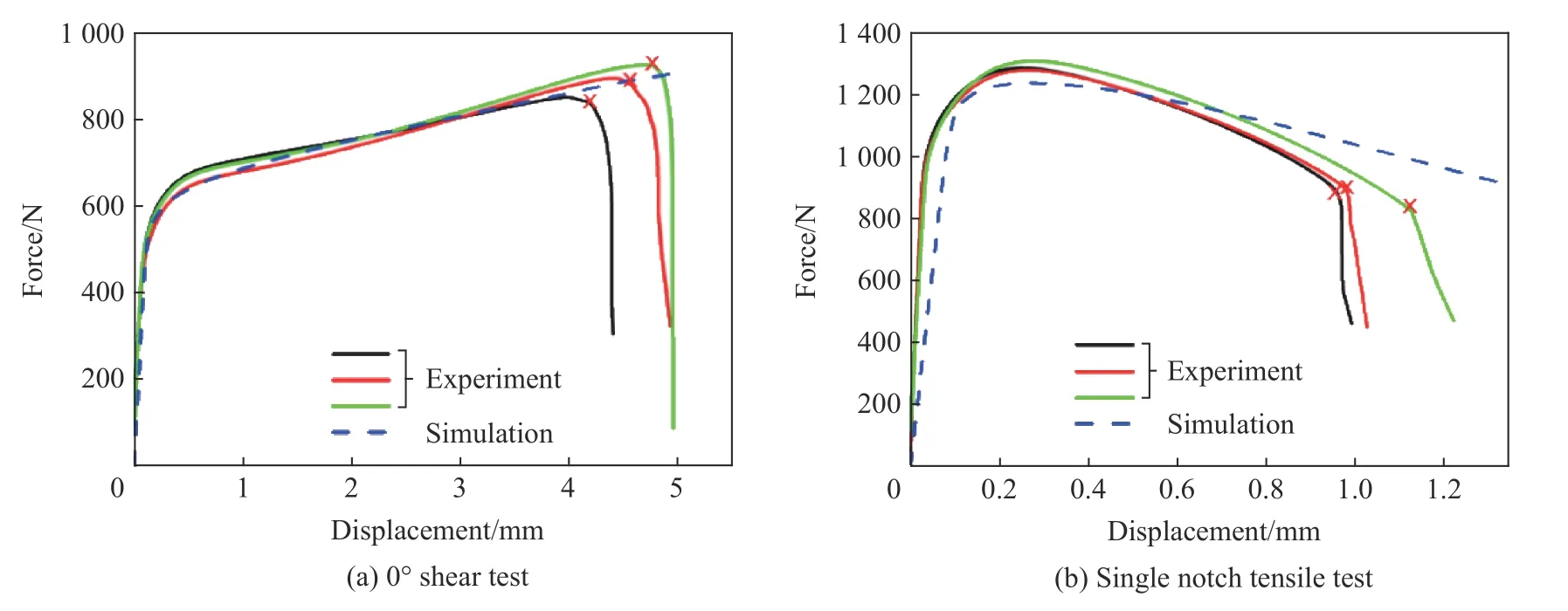
图6 模拟与实验获得的力-位移曲线Fig.6 Force-displacement curves according to experiment and simulation
图7给出了变形区的应力三轴度随宏观变形的演化过程。图中显示0°剪切实验中,变形区应力三轴度随着试样变形增大而缓慢上升,但上升幅度较小,加载方式仍是决定的应力三轴度的主要因素。为统一标准,在参数标定中选用全程应力三轴度的平均值,以更好地考虑应力路径对材料断裂应变的影响,相比文献中普遍采用初始三轴度进行参数标定的做法,更加合理。
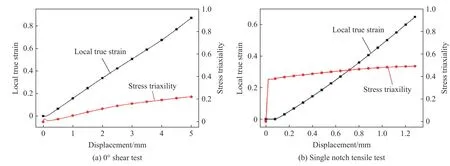
图7 变形区局部应变和应力三轴度曲线Fig.7 Evolution of the local strain and stress triaxiality in deformation areas
对于单轴拉伸和单双缺口拉伸实验而言,三种实验中试样的破坏形式相近,均为颈缩所致的拉伸破坏。因此,试样局部断裂应变还可以通过理论公式来估算。Gambirasio等[21]假定材料塑性体积不变,通过观测试样截面积的缩小即可估算试样的局部断裂应变。试样局部断裂应变εf的计算公式如下:
5)土方施工的压实作业。在填筑材料施工结束后,需要对其进行压实,保证土方的整体强度。在进行压实作业时,需要使用专门的压实设备进行操作,同时还需要对土方进行均匀性处理。

式中:A0、Af分别为初始和断裂时试样缺口处的最小截面积;A0=dt,t 为试件厚度;对单轴拉伸试样而言,d 为标距段宽度;对缺口拉伸试样而言,d 为两个半圆口中点之间的距离。为保证断裂应变计算的准确性,采用金相显微镜辅助测量断口的截面积,如图8所示:首先利用金相显微镜对断口正面和侧面拍照,然后利用图像处理方法统计断口宽度和厚度的像素尺寸,并根据标尺换算成真实面积。需要注意的是在拍断口侧面时,样品和显微镜必须垂直,所以用台钳夹住样品以保证断口竖直。
图9是变形区局部断裂应变随平均应力三轴度的演化过程。图中纵坐标的误差棒是指三个断裂应变的标准差(下同)。由于试样的断裂行为受多个因素影响,因此即使加载条件和样品加工都能精确控制,样品的断裂位置和时刻仍然会呈现一定随机性[22]。图中横坐标的误差棒表示变形区的应力三轴度在加载过程中偏离均值的程度。黑色方点代表的数据点是模拟结合实验获取的局部断裂应变,蓝色圆点代表的数据点则是通过图像法利用式(3) 计算得到的断裂应变。从图中可以看出图像法获取的断裂应变要比模拟实验结合法获得的普遍高出30%~50%。而且0°和45°剪切实验无法通过图像法获取局部断裂应变。从获取标准的一致性而言,模拟实验结合法获取的各应力三轴度下的断裂应变互相之间可比性更强,拟合参数的可信度也更高。图中根据式(2)第一项进行非线性拟合后得到的参数如下:D1= 0.284±0.075,D2=0.677±0.052,D3=−2.461±0.580。

图8 双缺口试样局部断裂应变Fig.8 Local fracturestrain of the double notch specimen
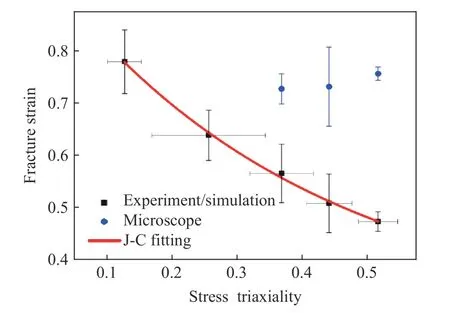
图9 归一化断裂应变随应力三轴度的变化Fig.9 Variation of local fracture strain with stress triaxiality
2.3 应变率效应
开展7种不同应变率(0.000 1、0.001、0.01、500、1 000、2 000、2 500~3 000 s−1)下的单轴拉伸和压缩实验,获得了室温条件下6008-T4铝合金在不同应变率下的拉伸真实应力应变曲线,如图10所示。为清晰起见,准静态数据只给出0.001 s−1下的曲线。所有准静态应力应变曲线是利用动态拉伸样品在Instron 试验机上获取的。主要原因是利用图2(a)所示的准静态国标样和图2(b)所示的动态拉伸样在同一应变率(0.001 s−1)拉伸下获得的试样断裂应变不同(分别约为15%和20%),两者在塑性变形段能很好吻合,但动态拉伸样的颈缩段要比准静态国标样的颈缩段更长。为了在同一标准下获取材料的断裂应变,动、静态拉伸实验均采用图2(b)所示的动态拉伸样。图10中显示相同塑性变形下动态加载相比准静态加载时流动应力更高,说明6008-T4铝合金具有轻微的应变率效应。图10(a)中箭头表示试样发生断裂的位置。特别地,在1 000 s−1应变率拉伸下,回收样品后发现样品已经发生断裂,但对比原始波形却发现入射波和透射波形的脉冲宽度相等,因此判定1000 s−1下样品断裂是多次拉伸造成的,对应的断裂应变数据不能用于参数拟合。
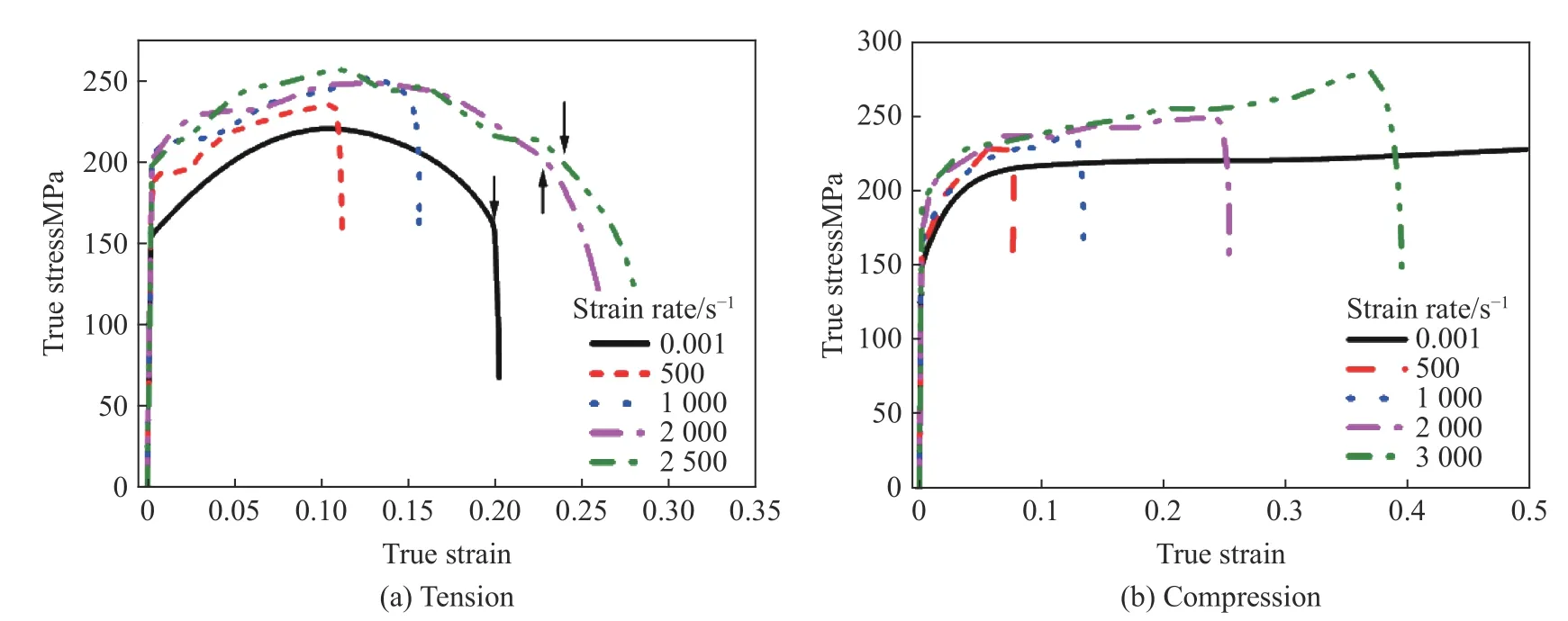
图10 不同应变率下室温铝合金单轴拉伸/压缩的真实应力应变曲线Fig.10 True stress-strain curves of aluminum alloys due to uniaxial tension/compression at different strain ratesand room temperature

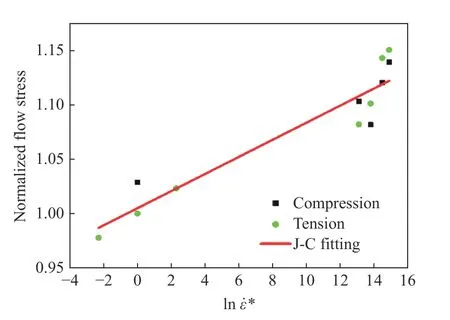
图11 应变为5%处的归一化流动应力Fig.11 Normalized flow stress at the strain of 5%
2.4 温度效应
在参考应变率(0.001 s−1)下开展5种温度(−50、25、100、200、300℃)的单轴拉伸实验,获得材料的真实应力应变曲线,如图13所示。图中显示随着环境温度升高,材料的屈服和流动应力以及应变硬化率都出现明显下降,而断裂应变则呈上升趋势。
图14是归一化屈服应力随环境温度变化的情况。因为指数拟合中要求指数不能为负,为充分利用实验数据,将参考温度选为−50℃,材料熔点取为888 K[23],屈服应力的归一化因子则选为−50℃时的屈服应力。通过对归一化屈服应力和数据T*进行非线性拟合,可以得到温度敏感指数m=1.06±0.12。图15是归一化断裂应变随环境温度变化的情况。线性拟合对指数正负性没有要求,因此仍以常温25℃作为参考温度进行温度归一化。断裂应变在温度从−50℃升高到常温时基本不变,明显偏离J-C 模型式(2)第三个因式所预测的线性关系。为保持J-C模型的原有形式并保证数据拟合的有效性,只针对常温和高温段的断裂应变数据进行讨论。通过对归一化断裂应变和T*进行线性拟合,得到温度敏感指数D5=1.60±0.17。至此本文获得了6008-T4铝合金所有J-C本构和损伤模型的参数,如表1所示。
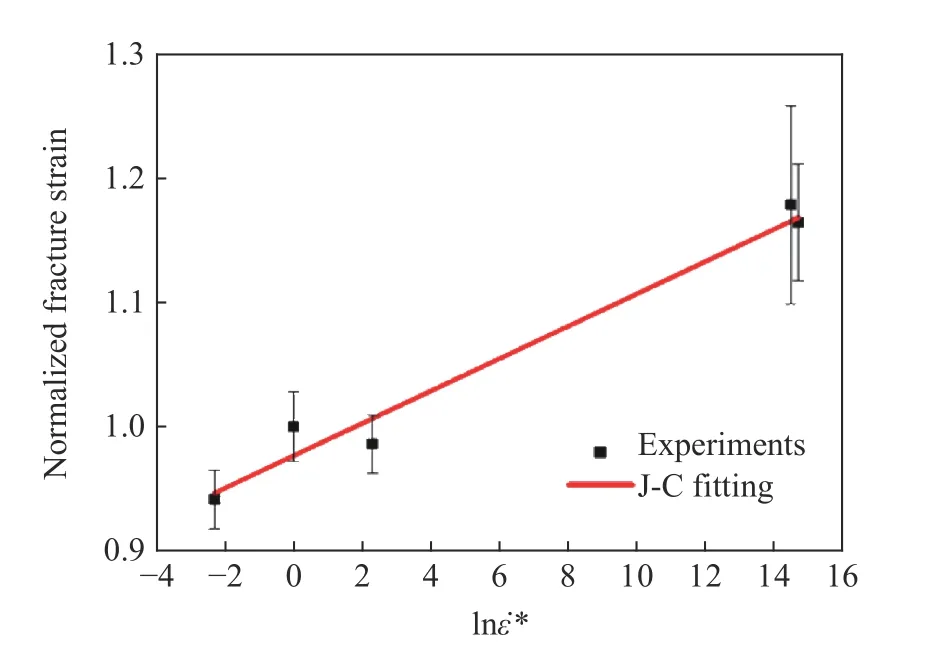
图12 归一化断裂应变随应变率对数的变化关系Fig.12 Normalized fracture strain varying with the logarithmic normalized strain rates
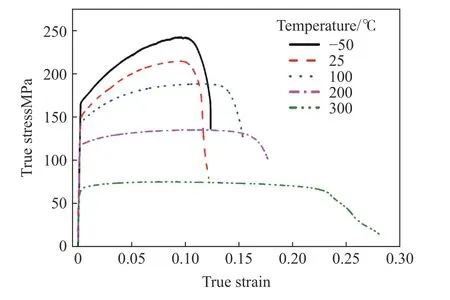
图13 不同环境温度下6008-T4铝合金准静态单轴拉伸真实应力应变曲线Fig.13 Quasi-static true stress-strain curves of 6008-T4 aluminum alloysby uniaxial tension at different temperatures
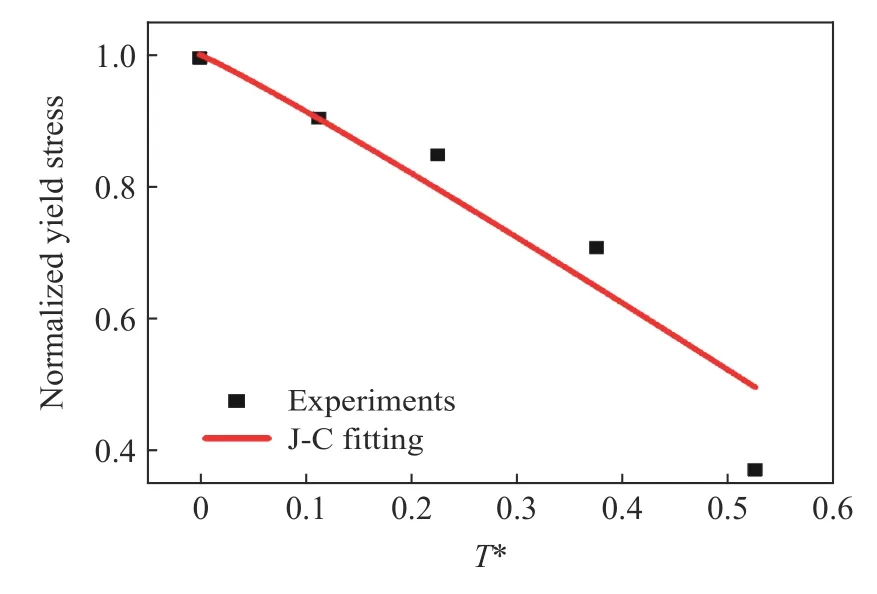
图14 归一化屈服应力随归一化温度的变化关系Fig.14 Normalized fracture strain varying with the normalized temperature
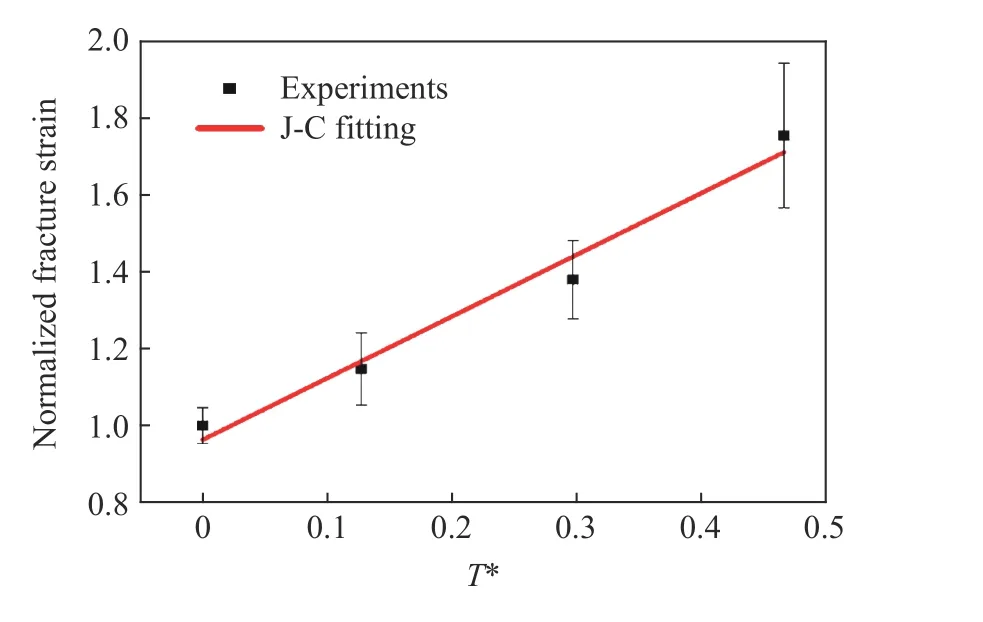
图15 归一化断裂应变随归一化温度的变化关系Fig.15 Normalized yield stress varies with the normalized temperature

表1 6008-T4铝合金J-C本构和损伤断裂参数Table 1 J-C constitutive and damage parameters of the 6008-T4 aluminum alloy
2.5 参数检验
由于材料塑性流动与应变率和温度相关,因此将不同应变率和温度下的实验曲线与J-C模型预测曲线进行比对,如图16所示。图中显示J-C模型可以较好地预测材料的的应变硬化效应和应变率效应。对温度实验而言,在不太高的温度(如−50~100℃)加载下,模型对整个塑性段预测较好;但到高温段,实验曲线的流动应力和应变硬化率比模型预测下降更快,J-C模型预测较差。考虑到J-C模型已经内置到很多商业有限元软件中,为了方便后续有限元模拟,本文仍然采用J-C模型的原始形式,对模型修正不作讨论。

图16 实验与J-C模型结果对比Fig.16 Comparison between experimental results and J-Cmodel predictions
为检验上述参数的准确性和参数标定方法的可靠性,本文利用一级气炮开展了平板侵彻实验。子弹材料选用45号钢,子弹形状和尺寸如图17所示。靶板加工成尺寸为50 mm×50 mm×2 mm 的矩形板,然后装夹到一个中心开孔(直径40 mm)的钢制背板(厚度2 mm)上。实验过程中钢子弹以240 m/s速度侵彻铝板,利用分幅相机SIM-X8记录子弹侵彻靶板以及后续的飞行过程;同时,回收靶板观察其破坏形貌。然后,利用所获取的6008-T4铝合金的J-C模型参数以及从文献中查找的45钢的J-C模型参数[14],通过Abaqus有限元软件模拟了与实验条件相同的平板侵彻过程,获取了相同弹速下靶板受侵彻破坏的过程以及破坏形貌。
实验和模拟中靶板受侵彻破坏的过程对比如图18所示。时间零点选为t1,即t1= 0,则t2=30µs,t3=60µs,t4= 90µs,t5=120µs,t6=170µs,t7= 230µs。以t1时刻的破坏形貌和子弹位置作为基准,将实验和模拟的时间零点对齐,然后对比t2~t7时刻靶板的破坏形貌和子弹位置及剩余速度等参数。图中显示实验和模拟结果吻合很好。实验和模拟中回收靶板的破坏形貌对比如图19所示。图中显示240 m/s冲击下靶板在自由面侧形成了“花瓣形”破坏断口,与模拟结果吻合良好。综上所述,本文中获取的模型参数以及参数标定方法都是可靠的。

图19 侵彻加载下靶板破坏形貌的实验和模拟结果Fig.19 Fracture morphologies of the target after penetration by experiments and simulation
3 结 论
对轨道车辆用6008-T4铝合金进行了多种力学性能实验,提出了一种新的获取断裂模型参数的实验方法,获取了6008-T4铝合金的J-C本构和损伤断裂模型参数;利用平板侵彻实验和有限元模拟验证了参数有效性,发现实验和模拟结果吻合良好,说明本文获取的模型参数以及参数标定方法都是可靠的。针对6008-T4铝合金的力学性能,获得如下结论:
(1)6008-T4铝合金的应变率效应在动、静态加载之间表现不太明显;随着应变率上升,材料屈服和流动应力增加较少,而断裂应变则有明显上升;
(2)6008-T4铝合金表现出明显的温度软化效应,即材料屈服应力随温度上升而发生明显下降,相应的断裂应变则明显上升;
(3)随着应力三轴度的增加,6008-T4铝合金的断裂应变明显降低,下降趋势符合J-C模型的理论预测。

