NEPE推进剂低高应变率下改进的黏-超弹本构模型*
孙政伟,许进升,周长省,陈 雄,杜红英
(1.南京理工大学机械工程学院,江苏 南京 210094;2.晋西工业集团有限责任公司技术中心,山西 太原030027)
固体推进剂在生产、运输、存储和发射过程中常受高应变率载荷作用,因此研究不同应变率对推进剂力学特性的影响在推进剂装药结构完整性分析中具有重要意义。硝酸酯增塑的聚醚聚氨酯推进剂(NEPE 推进剂)是一种由黏弹性基体和铝粉组成的高填充固体黏弹性复合材料[1]。作为一种新型推进剂,NEPE推进剂综合了双基推进剂和复合推进剂的优点,具有高能量的特点和优异的力学性能,近年来得到了广泛的应用。NEPE推进剂具有复杂的非线性黏弹性力学性能,因此必须要考虑有限变形下的加载历史、温度和应变率对材料力学性能的影响。
目前,在宏观研究领域常采用唯象学的方法来建立固体推进剂的本构模型。由于固体推进剂具有的超弹性和黏弹性力学特性,其本构模型通常包括多项式形式、Mooney-Rivlin 模型[2-3]、Ogden 模型[4]、Yeoh 模型[5]的超弹部分,以及Maxwell模型、Duncan 模型[6]、Schapery 模型[7]、朱王唐模型[8]的黏弹部分。常新龙等[9]在Burke 模型的基础上,考虑了温度和应变率效应,采用Mooney-Rivlin 应变能函数来描述稳态超弹响应部分,采用一个Maxwell 单元来描述动态黏弹响应部分,同时引入温度效应关系式,建立了一个黏超弹本构模型,该模型可以较好地描述HTPB推进剂在低中应变率下的压缩力学响应,但在应变率较高时误差会随着应变增大。杨龙等[10]通过低中应变率实验发现1 s−1为应力和应变率双线性关系的转折点,他在Mohotti 模型的基础上,将应变能函数与应变率对数线性联系起来,再结合应变依赖性建立了应变率相关的超弹本构模型。Wang 等[11]发现随着温度的不断降低和应变速率的增大,HTPB推进剂的应力-应变曲线和损伤特征更加复杂;考虑到温度对材料超弹性、黏弹性和损伤的影响,他基于HTPB推进剂的压缩行为和非线性黏弹性本构理论,提出了一种新的含损伤热黏超弹本构模型。Guo等[12]基于Lubliner 等提出的变形梯度的乘法分解和自由能的加法分裂,采用Attard 应变能函数,得到了有限变形下聚脲的非线性黏超弹本构模型,能够较好地描述宽泛应变率下聚脲的拉伸和压缩力学行为。
为了研究推进剂在受载时导致宏观变化的内在因素,近年来,许多学者使用细观方法,根据推进剂外部的受载情况,基于计算机颗粒堆积算法,构建出满足所需条件的细观数值模型,通过数值模拟得到细观结构对宏观力学行为的影响。韩龙等[13]将宏观研究方法与细观研究方法结合起来,基于黏弹性脱湿准则将获得的细观数值代入到宏观本构模型中,提出了一个考虑NEPE推进剂细观颗粒脱湿因素的非线性黏弹性本构模型。
分离式Hopkinson 杆(SHB)技术是目前对复合材料进行高应变率测试的主要方法。Davies[14]和Kolsky[15]首先提出了用两个Hopkinson 杆夹住试样来测量材料的动态响应的方法,后来经过众多学者的改进,分离式Hopkinson 杆技术已经可以用来对材料进行压缩、拉伸和扭转等多种加载形式的测试。
本文通过使用分离式Hopkinson 压杆(SHPB)和电子万能试验机,对NEPE 推进剂进行高低应变率单轴压缩实验,在Yang 等[16]提出的NLHV 模型的基础上,把松弛时间与应变率联系起来,构建一个非线性黏超弹本构模型。
1 本构模型
考虑到NEPE推进剂不仅具有卸载后应变可以基本恢复的超弹特性,同时还具有率相关性、加载历史相关性和松弛等黏弹特性,本文在Yang 等[16]提出的NLHV 模型基础上,采用Rivlin 应变能函数,并根据松弛时间和应变率之间的关系,将松弛时间替换成应变率相关的函数,建立了一个宽泛应变率非线性黏超弹本构模型,模型表达式如下:

1.1 超弹性本构方程

1.2 黏弹性本构模型
由于NEPE推进剂具有率相关性和加载历史相关性,在准静态和动态加载条件下都表现出明显的非线性黏弹特性,因此采用Truesdell 等[19]证明的非线性黏弹性本构方程:

目前,不同应变率范围内的加载过程通常使用不同阶数的Prony 级数来描述。从微观结构的角度看,弹性体在变形过程中,由于化学键的可逆断裂和交换发生了分子间滑移,从而产生了松弛现象。从宏观的角度来看,不同的应变水平下都存在一个整体的松弛时间(θ),Khajehsaeid 等[20]提出该松弛时间最终取决于变形率,通过如下关系将材料的整体松弛时间和变形速率联系起来:

将式(18)和式(19)代入式(17)可得

2 实 验
2.1 实验材料
由于NEPE推进剂是一种多组分的复合材料,不同批次的NEPE推进剂的力学性能也存在偏差,因此本文选择同一批次的NEPE 推进剂来进行实验,并将浇筑成型的管状药切割为两种尺寸。准静态实验使用公称尺寸为∅10 mm×10 mm 的试件,动态实验使用公称尺寸为∅ 10 mm×5 mm 的试件。
2.2 低应变率压缩实验

2.3 高应变率压缩实验
2.3.1试件尺寸设计

2.3.2实验方法及过程
高应变率动态压缩实验在分离式Hopkinson 实验台上进行。由于NEPE推进剂较软,波阻抗较低,为了获得较为准确的透射信号,选择LC4铝制作了本实验的子弹、入射杆、透射杆和吸收杆。在实验过程中,为了减少试验杆与试件之间摩擦带来的影响,在试件端部涂上适量的润滑脂。为了保证实验数据的可靠性,试件内必须满足恒应变率变形和应力均匀条件,使用脉冲整形技术,将厚纸片置于入射杆端部,提升入射脉冲上升沿时间,达到恒应变率变形。在室温下分别进行5种不同应变率下的实验,每个应变率下重复5组实验以获得较为准确的数据。
使用二波法对数据采集系统获得的信号进行处理,获得试件的应力应变曲线和应变率:

式中:c0为杆中的弹性波波速;l0为试件的初始长度; E0为杆的杨氏模量; S0为杆的横截面积; Ss为试件的初始横截面积,εR和εT分别为反射应变和透射应变。
2.4 实验结果分析
2.4.1高应变率实验可靠性分析
为保证实验结果具有有效性和可信性,需要对每次的实验数据进行应力均匀性和恒应变率加载校核。图1为0.12 MPa 炮压下的SHPB实验波形。图1(a)为应变片测得的原始波形,由式(25)可知试件的应变率与反射波强度成正比,图中可以看出反射波呈平台状,因此满足恒应变率加载要求。图1(b)为实验透射波和计算透射波的对比波形,通过将入射波和反射波进行平移相加获得计算透射波,对比发现实验透射波和计算透射波基本重合,说明实验满足应力均匀性假设。
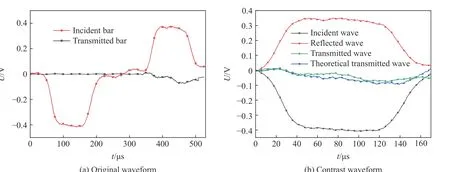
图1 SHPB实验波形图Fig.1 Waveprofilesby SHPB experiment
2.4.2应力应变曲线分析
通过对万能试验机上采集到的数据进行处理,可以获得室温下试件不同应变率的应力应变曲线,如图2所示。由图2可知,随着应变率的增加,NEPE 推进剂的弹性模量明显增大,硬度增加;在曲线中并未找到明显的屈服点;在应变率较低时,曲线接近于直线,当应变率达到8.333×10−1s−1时,表现出明显的非线性且存在应力强化段。
对满足恒应变率变形和应力均匀性的高应变率实验数据进行处理,可以得到高应变率下试件的应力应变曲线,如图3所示。通过观察可以发现,在加载过程中,试件经历了初始弹性上升段、屈服阶段和屈服后应力下降阶段,应力达到峰值后的下降段可能是由于子弹长度有限,产生的应力波作用时间有限,导致了试件内应力被卸载,并不一定是材料结构破坏造成的;材料的性质具有明显的率相关性,随着应变率的增加,材料的强度、屈服应力和弹性模量显著增加,与低应变率相比,材料的应变率敏感性更高;由于高速冲击下材料内部瞬间产生大量热量无法及时散发出去,使得材料内部温度升高,导致了材料出现软化效应,力学性能降低,同时在高速冲击下材料内部结构遭到破坏,颗粒发生了破碎,因此材料在屈服后出现了短暂的应变软化段,然后出现了应力下降段。
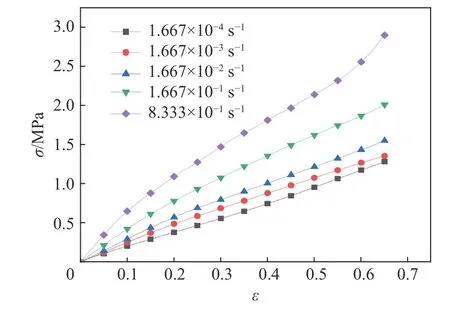
图2 低应变率下的应力应变曲线Fig.2 Stress-strain curves at low strain rates
准静态实验后获得的恢复试件如图4和图5所示,通过观察试件可以发现,对试件进行70%应变的压缩后卸载,卸载后与初始长度相差0.81 mm,静置24 h 后试件几乎可以恢复初始长度,与初始长度相差0.47 mm,基体未产生裂痕和发生断裂;当应变提升至95%时,卸载后与初始长度相差2.1 mm,静置24 h 试件长度与初始长度相差1.3 mm,基体仍未产生裂痕和发生断裂,试件呈现出鼓状,说明材料较软且具有较好的弹性和延展性。在准静态压缩实验中,试件内部颗粒与基体的黏合处会产生应力集中,颗粒脱湿形成横向的孔洞并产生微裂纹,随着应变增大,微裂纹增多,但并未进一步发展成断裂破坏。高应变率实验获得的试件则不同,如图6所示,试件主要分为3种形态,当应变率较低时呈鼓状,此时颗粒受到冲击发生破碎,试件侧面出现裂痕,但试件基体还未发生完全断裂;当应变率升高时,此时裂痕由试件边缘向内扩展,造成基体内部发生破坏,试件断裂;随着应变率继续升高,试件被完全打散,颗粒破碎程度增加,基体被压成片状,试件内部被完全破坏,产生了大量裂痕和空隙,基体发生解体现象。在冲击实验中,由于颗粒的模量远大于基体的模量,大部分的冲击载荷会作用在颗粒上,导致部分颗粒还未脱湿就发生破碎,微裂纹从颗粒内部产生并向基体延伸,推进剂发生穿晶断裂,随着应变率增加,颗粒破碎程度增大,基体解体现象更加明显。

图4 准静态实验后获得的恢复试件(应变为70%)Fig.4 Recovered specimens after quasi-static compression at the strain of 70%

图5 准静态实验后获得的恢复试件(95%应变)Fig.5 Recovered specimensafter quasi-static compression at the strain of 95%

图6 动态试件Fig.6 Specimens after dynamic compression
3 模型拟合与预测
采用最小二乘法对准静态实验中速率为0.1 mm/min 的数据与Rivlin 超弹模型进行拟合,获得的Rivlin 超弹模型参数和相关系数见表1。图7是应变率为1.667×10−4s−1时的实验曲线和拟合曲线,可以看出拟合曲线与实验数据基本重合,超弹参数能较好地反映材料的非线性弹性响应。
对于恒应变率变形,伸长率为关于时间的函数

表1 Rivlin超弹模型参数Table 1 Rivlin fitted parameters
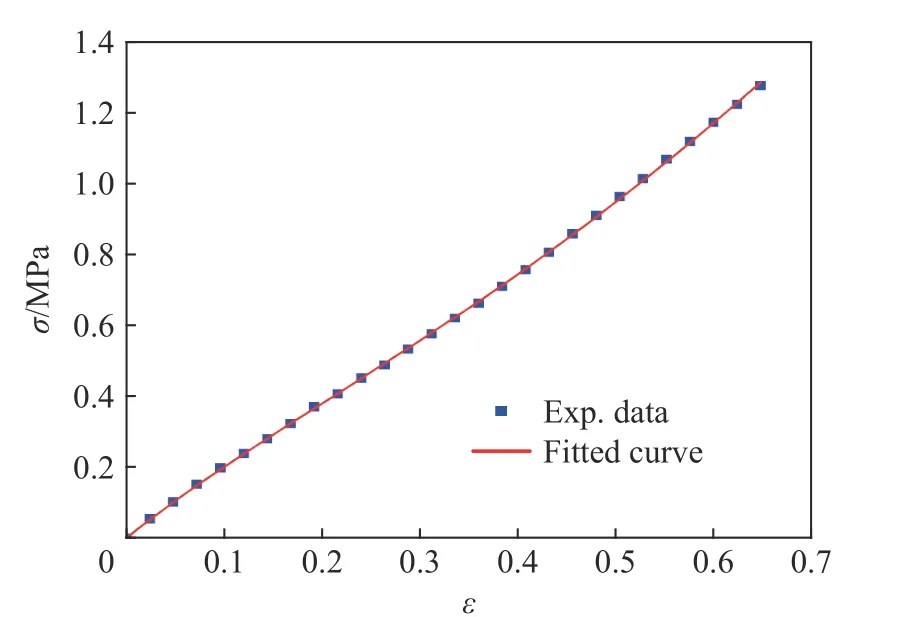
图7 Rivlin 超弹模型准静态实验拟合曲线Fig.7 Rivlin model fit to quasi-static experimental data

松弛函数G (t)可以化为
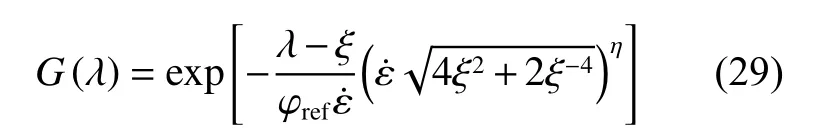
当进行宽泛应变率拟合时,式(23)可化为
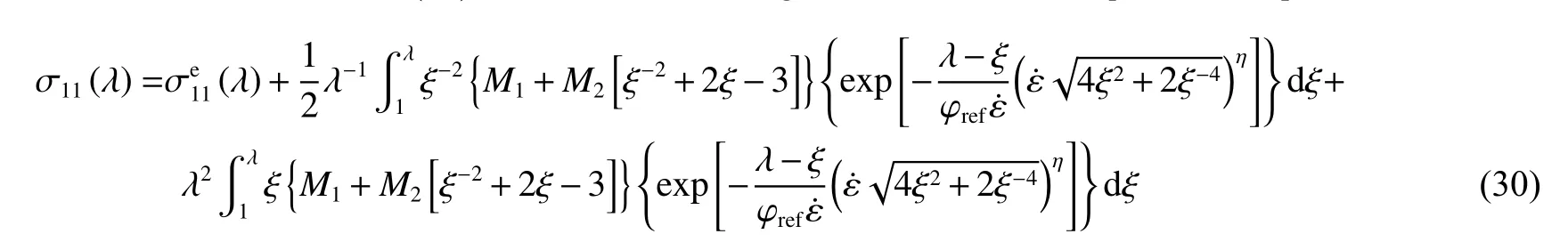
分别对准静态压缩实验和分离式Hopkinson 杆实验获得的数据进行处理,获得应力应变曲线,转化成应力和伸长比代入式(30),采用最小二乘法进行拟合,获得黏弹参数如表2所示。图8是包含了准静态压缩实验和分离式Hopkinson 杆实验的实验曲线和拟合曲线。由图中可以看出,在低/高应变率范围内,拟合曲线与实验数据具有较好的重合度,能够较为准确地描述低/高应变率下NEPE推进剂的应力应变关系。
利用本文建立的黏超弹本构模型对单轴压缩速率为500 mm/min 的准静态实验和应变率为4 500 s−1的动态压缩实验进行预测,预测曲线和实验曲线如图9所示。从图9中可以看出,实验曲线与预测曲线具有较好的一致性,可以较为准确地描述NEPE推进剂在低高应变率下的力学响应;在高应变率情况下,当应变大于0.45时实验曲线逐渐偏离预测曲线,出现应变软化现象,这是由于在冲击实验中响应时间十分短暂,实验过程中的产热速率远大于热扩散速率,此时材料内部的温度急剧升高造成了材料的软化。本文没有考虑在高速冲击下材料内部温升对材料的软化效应,因此造成了高应变率下当应变大于0.45时,预测曲线高于实验曲线的现象。

表2黏弹参数Table 2 Viscoelastic parameters
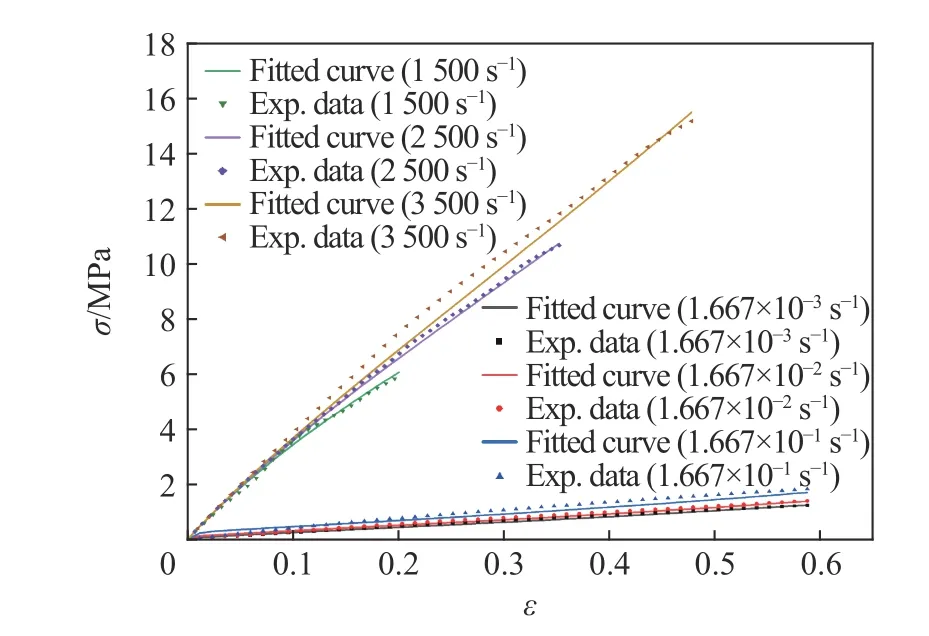
图8 低高应变率下实验曲线与拟合曲线Fig.8 Comparison between fitted resultsand experiment data at low and high rates
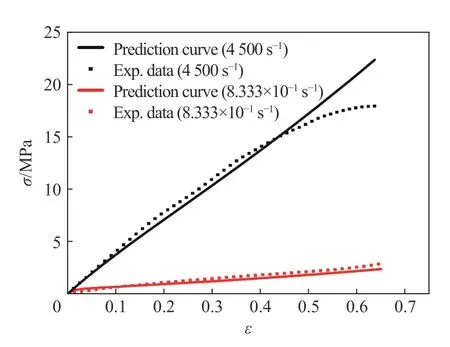
图9 低/高应变率下实验曲线与预测曲线Fig.9 Comparison between prediction curves and experiment data at low and high rates
4 结 论
本文建立的黏超弹本构方程由超弹部分和黏弹部分组成,首先用极慢速压缩实验数据拟合出超弹参数,然后使用准静态和动态实验结果拟合出其他参数。通过预测曲线和实验曲线对比可以看出,本文提出的本构模型能够较为准确地描述NEPE 推进剂在低应变率和高应变率下的力学行为。
考虑到松弛时间是具有率相关性的,本文采用了一个率相关松弛函数来替代传统的Prony 级数形式。与Prony 级数形式相比,该函数减少了材料黏弹参数的数量,同时说明了松弛时间与应变水平有关联。
与准静态实验相比,材料在冲击实验中具有更高的应变率敏感性。在高速冲击下材料内部瞬间产生大量热量无法及时散发出去,使得材料内部温度升高,导致了材料出现软化效应,力学性能降低,同时在高速冲击下部分颗粒还未脱湿就发生破碎,微裂纹从颗粒内部产生并向基体延伸,推进剂发生穿晶断裂,随着应变率增加颗粒破碎程度增大,基体解体现象更加明显,破坏形式通常表现为鼓形变形、试件断裂和完全破坏三种。

