基于数据挖掘技术的地下工程目标毁伤效应计算方法*

张 磊，吴 昊，赵 强，王 幸，任新见，王继民，孔德锋

（1.军事科学院国防工程研究院工程防护研究所，河南 洛阳 471023；2.军事科学院，北京100071；3.河海大学计算机与信息学院，江苏 南京211100）

武器毁伤效应是攻防双方都十分关注的基础性和共性的问题，对武器的研制、目标的防护设计、易损性研究和毁伤评估都具有举足轻重的作用，是承接“进攻-防守-评估”作战要素的核心环节。武器毁伤效应的主要研究手段包括实验研究、理论分析和数值模拟[1]，其中解析法一般需对毁伤过程做一定的简化假定，只能适用于简单条件；数值模拟则过度依赖于算法和模型，参数多且计算速度慢，无法满足实战要求；实验研究是最可靠、最常用的手段。尽管随着国防事业的发展，我国科研人员已经积累了一定数量的实验数据（包括训练、演习和实战等数据）、经验算法和毁伤判据等效应数据，但现有数据仍存在离散性大、数据缺失、数量少、噪声大、分布不均匀、不连续、分布范围窄等缺点，无法支撑毁伤效应计算和评估所需，其需要建立足够精度、宽域分布且连续的毁伤谱。数据挖掘技术的出现为此类问题的解决提供了可行途径，数据挖掘通常又称“数据中的知识发现”，是从大量的、有噪声的、不完全的、不连续的、模糊的、随机的实测数据中提取有效的、新颖的、潜在有用的信息的过程，是将数据变成有价值信息的过程[2]。近年来数据挖掘技术已经在工业意外爆炸、高速穿甲、装甲防护等领域中得到应用。He等[3]首次将过程挖掘技术应用于煤矿瓦斯爆炸事故的紧急救援领域，将2006年至2014年下半年期间我国煤矿发生的50起重大瓦斯爆炸事故作为日志数据，利用过程挖掘技术提取应急救援模型并在紧急事故救援中得到成功应用。Ryan 等[4]开发了一种多层感知器体系结构人工神经网络模型用于预测铝质弹丸超高速撞击Whipple防护盾的贯穿极限，利用769次冲击试验数据训练神经网络模型，预测精度达92%，高于经验方法的71%准确率。Ryan 等[5]还分析了超高速撞击Whipple防护盾的研究中，传统人工神经网络在类似高维空间问题研究中的不足（特别是当试验样本不足、分布范围窄且分布不均匀时，人工神经网络预测精度会大大降低），并提出一种通过最少量额外实验数据来补救采样不良的参数空间影响的算法。李建光等[6]利用RBF神经网络模型对混凝土侵彻深度进行预测。金胜兵等[7]利用数据挖掘技术进行了混凝土靶标侵彻深度的预测，综合了k-近邻（k-nearest neighbor,KNN）算法与BP神经网络模型，提高了现有神经网络模型的预测精度。

在现代战争中，大量具有战略价值的目标被移入地下，依靠高抗力地下防护结构抵御来袭武器毁伤。为提高对地下目标的毁伤能力，钻地武器研发和应用发展迅速。钻地武器依靠动能来穿透防护层、钻入工程内部或侵彻到地下一定深度后爆炸，从而对目标产生毁伤，近年来在实际战场中得到多次应用。因此，常规钻地武器对地下目标的毁伤效应和毁伤评估一直是研究热点。杨秀敏等[8]曾对钻地武器破坏效应的研究现状和发展进行了系统的论述，指出常规钻地弹毁伤效应包括侵彻效应和爆炸效应，其中爆炸效应包括岩土介质中的冲击波（即地冲击）和空气冲击波带来的两方面效应，研究结果表明：由于钻地武器对地下目标毁伤效应的复杂性，以实验数据为基础的经验统计方法具有重要作用。张国星等[9]就钻地弹侵彻地下工程目标研究现状进行了综述，分析了实验研究、解析方法和数值模拟的优缺点，并指出实验方法是其中最为成熟的方法，同时也指出数值模拟方法也是重要的技术手段之一，但计算速度仍限制了其应用。此外，文献[10-11]利用数值模拟进行了钻地武器对地下工程目标的毁伤效应分析和评估，讨论了影响毁伤效应的主要战斗部参数和目标参数。综上所述，在钻地武器对地下目标毁伤的研究中，特别是在实战条件下需要对战场目标的毁伤进行快速评估的情形，实验研究以及以此为基础的经验方法是一种重要的技术途径。

目前通过数据挖掘进行毁伤效应分析，主要是基于实验数据建立各种浅层或深层网络预测模型，但是现有实验数据存在离散性大、缺失明显、数量少、数据噪声大、样本分布不均匀、不连续、分布范围窄等缺点，以至于训练出来的模型无法满足参数域的需要。本文针对钻地武器对地下工程目标的毁伤，构建基于效应试验和经验算法融合的数据挖掘毁伤效应算法：以效应源数据为基础，通过数据异常分析算法剔除数据异常点，建立毁伤源数据库；针对经验算法适用范围有限、计算精度不统一等局限性，建立经验算法评价方法，分析不同参数域内最适用的经验算法；利用实验数据建立神经网络预测模型；在此基础上建立基于k-近邻算法、经验算法和BP神经网络模型的毁伤效应“三阶段”算法进行钻地武器对地下工程目标毁伤效应计算。

1 源数据异常分析

源数据蕴涵分析对象运行的客观规律，其完整性和可靠性是确保数据挖掘能否进行以及挖掘结果能否正确的前提，因此，源数据是数据挖掘的基础和核心。以钻地武器对地下工程目标毁伤效果评价为例，分析过程中所需源数据包括图1所示的数据种类。

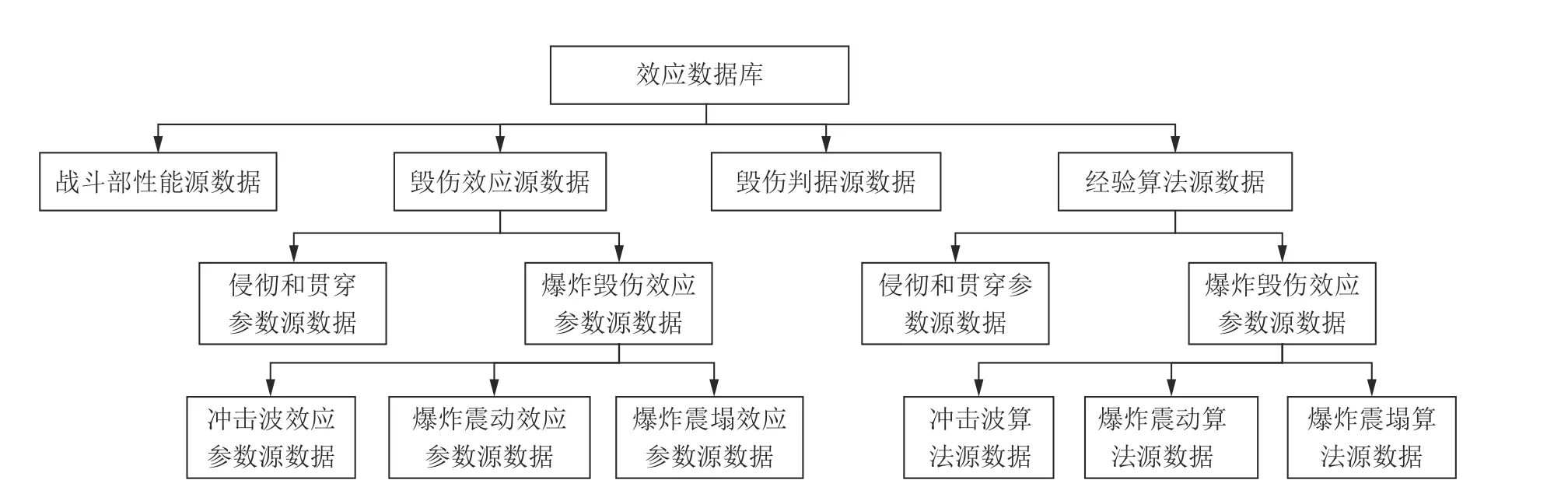
图1 地下工程目标毁伤评估源数据结构Fig.1 Structure of source data for underground engineering target damage assessment

在源数据中，由于实验条件的差别、量测技术和标准的差异、实验误差、人为因素以及记录和数据录入失误等不可避免的因素，会导致一些样本不符合数据模型的一般规则，或者与其他样本存在较大的偏差，这样的样本即为“数据异常点”。异常数据会降低一些数据挖掘算法的效率，可能会在数据模型中引入非正态分布或其他的数据复杂性，从而很难以可行的计算方式找到准确的数学模型。因此，必须对进入数据库的源数据进行数据异常点的检测和清除。考虑到毁伤源数据维度高、各维度量纲和尺度不一致，且各个维度变量存在相互关联性等特征，选用马氏距离（Mahalanobis distance,记为di）作为数据异常性判断参数，计算各数据与数据集均值的距离，距离均值超过± 3σ的数据点认为是异常数据。

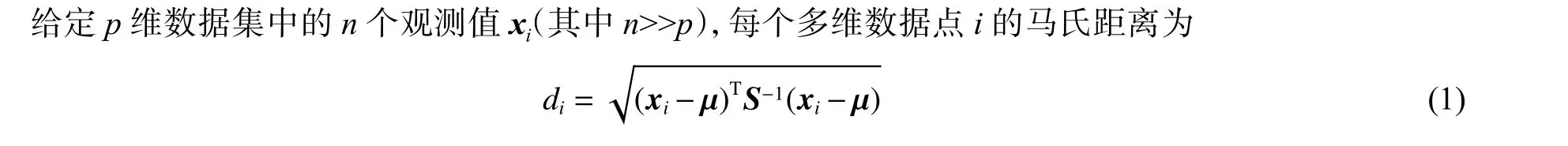
式中：µ为均值向量，S 为协方差矩阵。图2为数据库中456个混凝土侵彻深度试验数据样本在剔除异常点前后马氏距离分布频率对比，在剔除16个与平均值相差超过± 3σ数据点后，保留下的440个数据样本离散性明显减小，其分布也更为吻合正态分布特征，选取这些数据样本能有效消除偶然因素引起的数据异常，提高预测精度。

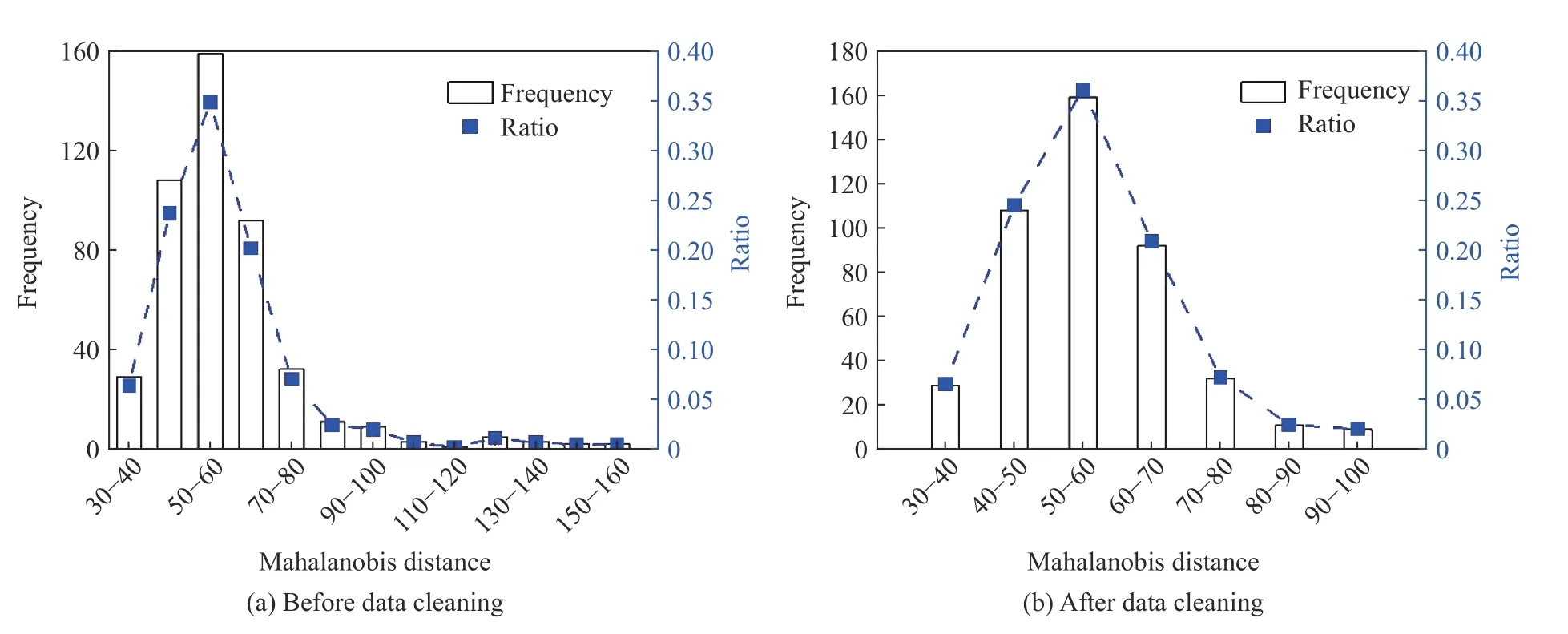
图2 数据样本频率分布图Fig.2 Frequency distribution of data sample

2 经验算法评价方法

实验研究尽管存在成本高、数据不连续以及适用范围有限等缺点，但以此为基础所建立的经验公式，往往在实验数据范围内具有较高的预测精度，且其形式简单，可根据几个有限的控制参数快速给出能满足实际工程精度需求的预测结果。但经验算法也存在明显的不足，经验算法是根据大量现场或实验测试数据，借助回归、拟合等统计分析方法建立，由于现场或实验测试数据都是在某些环境因素下得到的，因而具有一定的适用范围或应用条件。如何评价这些算法在不同参数范围内的优劣，是得到相对准确预测结果的前提。

本文采用如图3所示的算法流程进行经验算法适用性判别。首先计算经验算法与实验数据样本的平均相对偏差，以与实验样本偏差小的算法作为最优算法；如果实验数据样本不足，再利用多个经验算法生成“伪效应试验数据”，计算不同经验算法之间的相对偏差，以相对偏差小的算法作为最佳算法；如果通过以上两个流程仍无法确定最佳算法时，则利用专业知识进行判断，分别从理论分析和使用者评价两个角度去判断算法优劣。

图3 经验算法评价流程Fig.3 Evaluation process of empirical algorithms

3 基于BP 神经网络的效应预测建模

3.1 BP神经网络基本原理

BP神经网络是应用最广泛的神经网络模型之一，其模型结构简单且具有强大的非线性映射能力，几乎可逼近所有非线性系统。它包括一个输入层、若干个隐藏层和一个输出层，输入层和输出层的节点数可以根据数据集的输入输出进行调整，隐藏层的层数和节点数可以根据训练的需要进行调整，同一层上节点不相互连接，层与层之间的神经元相互连接，网络中每一个节点都是一个独立的神经元。

BP神经网络的训练过程是一个全局优化的问题，通过最小化损失函数，可以得到最优的网络参数，它的训练过程由信号的正向传播与反向误差传播两个部分组成。

式中：pi为预测的效应值，ti为样本效应值，n为样本数。

（2）在误差反向传播阶段，误差从输出层输入，然后沿着梯度下降的方向向隐藏层和输入层逐层返回，并修改每一层神经元的权值和偏置项。当误差减少到可以接受的程度或训练达到指定的次数时，则模型训练停止[13]。

钻地武器对地下工程毁的伤过程涉及侵彻贯穿、空气冲击波、爆炸震动和爆炸震塌等不同的毁伤效应，需对每个毁伤效应分别设计神经网络模型。为消除不同特征单位差异对模型的影响，对各效应的主要控制参数进行无量纲化：

式中： x1,x2,···,xn和Y 为无量纲化量。无量纲化可以消除各变量之间的相关关系，同时减少模型输入变量，降低维度。

3.2 神经网络模型结构

（1）模型输入层

模型输入为无量纲化产生的控制参数向量（ x1,x2,···,xn）。

（2）模型隐藏层

Fletcher 等[14]的研究表明：一般三层的神经网络就可以逼近任意的函数，而增加隐藏层的数量可以显著提高模型的预测精度，但同时也会使得模型计算更加复杂，模型训练需要更多的时间，一般可采用经验公式计算隐藏层的数量。本文利用下式确定隐藏层的层数：

式中：N 为输入层节点数量。在确定隐藏层的数量之后，对于每层的神经元节点数目的确定目前没有较好的公式或方法可以参考，实际研究中一般使用人工试错法和经验法进行结合来确定。

（3）模型输出层

输出层神经元个数为1，表示输出的效应量，即式(3)中的Y。

模型激活函数选用Relu 矫正线性单元激活函数，结合数值试验调整学习速率为0.05，既能保证训练的速度，又能保证模型的稳定性和精确度。

3.3 模型实验验证

（1）实验方法

（2）实验数据

从源数据库中抽取实验数据837条，并通过异常分析剔除异常数据，最后用于建模的数据为815条，其中570条作为训练集，245条作为验证集。

（3）实验结果及分析

BP 神经网络和BRL、Young、NDRC和Forrestal经验算法[15-18]计算后的在验证集上的MAPE 指标见表1。由于所选取的测试集为随机从效应数据库中抽取，样本分布比较离散，部分区间样本点会超出经验公式适用范围，从而导致经验算法整体预测效果不佳，而BP神经网络在测试集上的MAPE明显比其他四个经验公式要低，其预测的总体效果要略优于其他四个经验公式。

表1 经验算法和BP 神经网络模型MAPE值Table 1 MAPE valuesof empirical algorithms and BP neural network model

4 毁伤效应计算“三阶段”算法

“三阶段”数据挖掘算法充分利用了源数据、经验算法以及BP神经网络模型的各自优点计算毁伤效应，可提高不同参数区间的效应预测准确率。“三阶段”法的基本思想为：如果输入参数与源数据（实验数据）中的样本接近，则认为通过实验结果即可给出可靠的效应预测；如果输入参数在经验算法的适用范围，则利用经验算法可得比较准确的计算结果；否则，利用实验数据组成训练样本，通过BP神经网络充分挖掘数据中的规律，利用神经网络模型给出预测结果。“三阶段”法的具体步骤为：首先采用k-近邻算法从源数据中检索与输入参数相似的效应过程，结合专业知识判断效应结果的合理性；若计算结果不满足要求，则从该参数区间中选择最优经验算法进行效应计算；若上述两种方法都无法给出合理结果，采用BP神经网络进行效应预测。流程如图4所示。

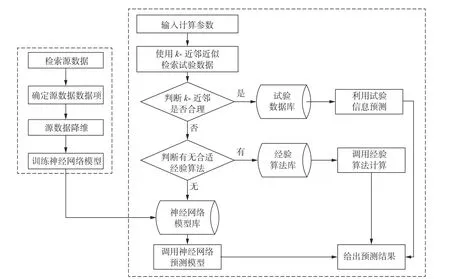
图4 “三阶段”法毁伤效应数据挖掘流程Fig.4 Flow of damageeffect data mining based on “three steps”

4.1 基于k-近邻算法的毁伤效应计算

相近的输入参数，其对应的效应预测输出结果应该是相似的，因此采用k-近邻算法[19]从源数据中检索与输入参数相似的k 个记录，并按照与输入参数距离的远近排列输出，供用户判断。

（1）毁伤效应主要控制参数

毁伤效应影响因素繁多，直接采用所有影响因素进行k-近邻检索会由于“维度灾难”导致检索效率低下以及结果不准确，因此需要对参与计算的数据进行降维。常用的数据降维方法有特征选择和特征提取，其中特征选择也称特征子集选择或属性选择，是指从已有的M 个特征中选择N 个特征使得特定指标最优化，是从原始特征中选择出一些最有效特征以降低数据集维度的过程；而特征提取是指利用已有的M 个特征计算出一个抽象程度更高的包含M 个新特征的特征集，并从中选择N 个重要的子特征，最终被选中的每个特征都是原始M 个特征的线性或非线性组合。本文采用特征选择进行数据降维。由于源数据实际采集的数据特征有限，而且一般常用经验算法已经比较全面地考虑了不同控制参数对效应的影响，因此，本文根据专业知识以及常用经验算法的控制变量来进行人工特征选择，确定毁伤效应的主要控制参数以达到数据降维的目的。以混凝土侵彻深度为例，通过人工选择，确定主要控制参数包括弹体质量、弹体直径、靶标强度、靶标密度和着靶速度等。

（2）相似度量函数

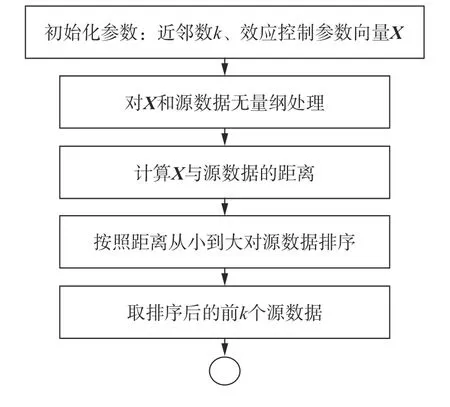
图5 基于KNN 的相似检索流程图Fig.5 Flow chart of similar searching based on KNN

如果输入参数在实验数据附近，那么直接通过检索到的实验数据就可以给出比较准确的效应计算结果；如果输入参数距离实验数据较远，即使检索到输入参数的k-近邻算法也无法得到准确的效率计算结果。为此，就需转入第2步：基于经验算法的毁伤效应计算。

4.2 基于经验算法的毁伤效应计算

利用输入参数所在参数区间的最优经验算法进行效应计算，并人工进行结果的有效性判断。如现有经验算法无法适用或计算精度较低，则转入第3步：基于BP神经网络模型的毁伤效应计算。

根据钻地武器对地下坑道工程目标毁伤过程，模型所涉及的毁伤效应算法主要包括：岩石靶标侵彻深度算法、混凝土靶标侵彻深度算法、土靶标侵彻深度算法、分层岩土介质靶标侵彻深度算法、坑道内空气冲击波效应算法、爆炸震塌效应算法和爆炸震动效应算法。对每一类算法，通过图3所示的算法评价流程，给出参数区间最优算法作为模型算法。

4.3 基于BP 神经网络的毁伤效应计算

由于实验数据分布范围有限，经验算法的适用范围、计算精度有限，以及复杂效应经验算法尚有明显缺失。因此，在前两者都无法给出合理结果的情况下，利用BP神经网络模型进行计算，给出毁伤效应计算结果。具体建模过程已在第3节进行介绍。

5 算法应用

钻地战斗部对地下工程目标毁伤是由侵彻和贯穿、爆炸震动和爆炸震塌、空气冲击波等多个有着前后顺序的过程组成，每个独立的过程对应一种毁伤元的毁伤效应。对每个过程都采用“三阶段”法进行计算，并根据上一过程的计算结果确定下一个过程的初始条件，所需主要参数和毁伤计算流程见图6。根据以上计算流程，开发计算软件。

经人工特征选择后确定的主要输入参数如表2所示，主要包括弹体参数、着靶参数、坑道结构以及围岩和衬砌材料特性等参数，其中弹体参数可根据战斗部型号由计算软件从底层数据库中自动读入，坑道类型、围岩材料种类和衬砌材料种类根据模型所提供的参数选择。

计算软件采用图6中的计算流程，首先根据弹体参数、着靶参数和围岩及衬砌材料等参数，计算弹体侵彻深度。通过“三阶段”算法，模型调用经验算法计算侵彻深度，计算结果为1.99 m。根据侵彻深度计算结果、弹着点坐标、防护层厚度等参数，判断爆心位置为“坑道顶部防护层内爆炸”。根据图6的计算流程，需要计算防护层爆炸震塌以及爆炸震动毁伤，爆炸震塌采用“三阶段”算法选用经验算法，计算结果表明不会产生爆炸震塌；爆炸震动毁伤由于无相临近实验数据，无法采用k-近邻算法，同时现有工程算法在适用范围上无法满足需求，因此模型会调用爆炸震动神经网络模型进行计算。

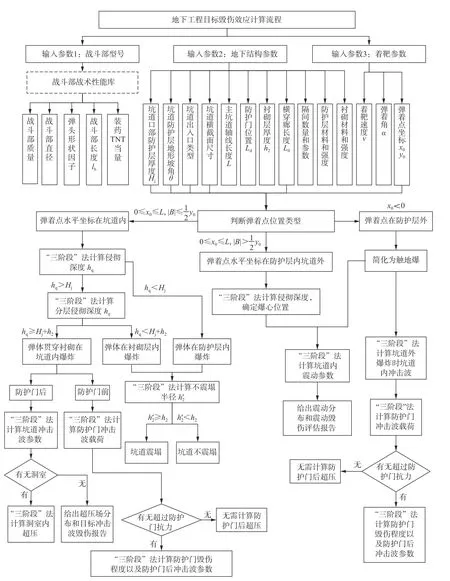
图6 地下工程毁伤效应计算流程图Fig.6 Calculation flow chart of damageeffect to underground engineering

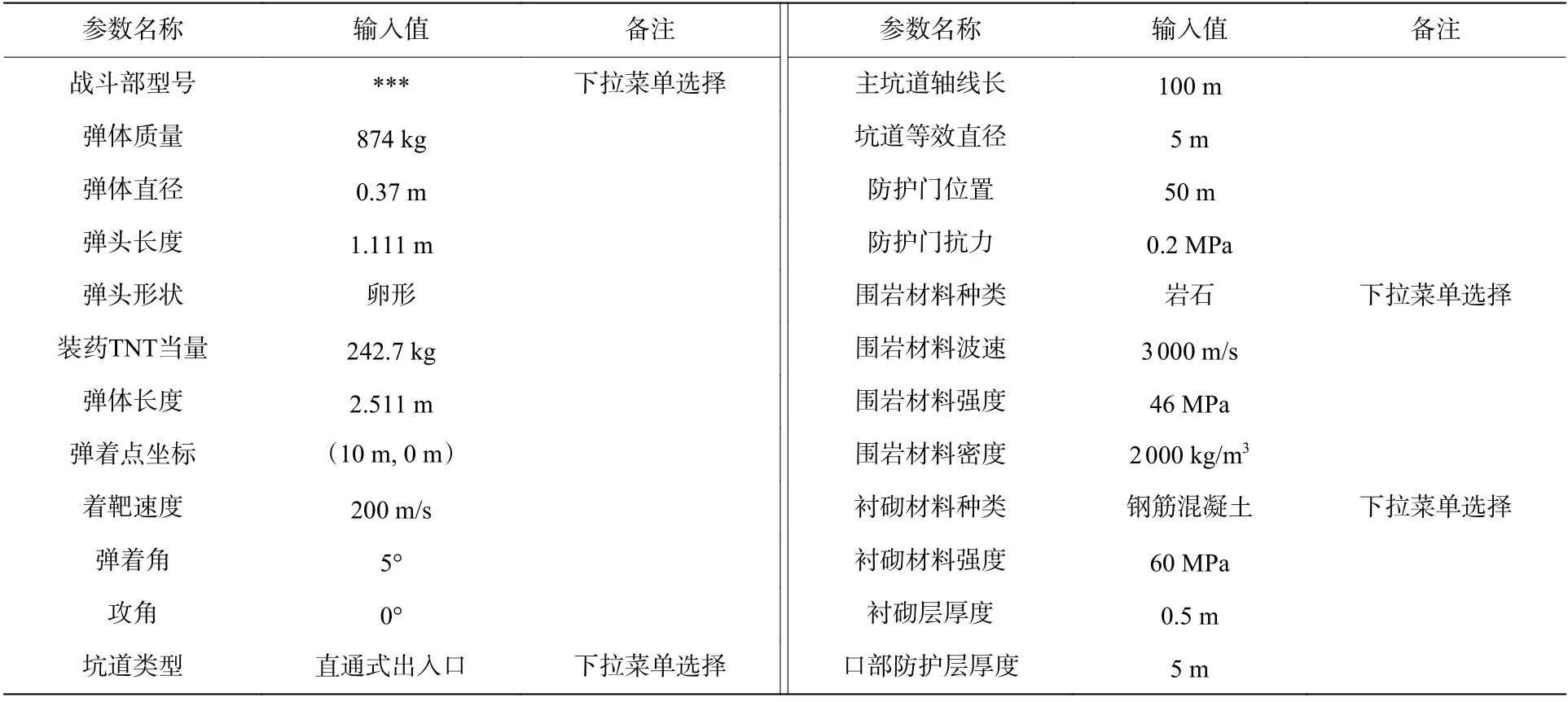
表2 地下工程毁伤计算所需主要控制参数Table2 Main control parametersrequired for damage calculation of underground engineering

6 结 论

本文以毁伤效应试验数据库为基础，采用数据挖掘技术，实现了钻地武器对地下坑道工程目标毁伤效应的快速计算。取得的主要研究成果如下：

（1）针对常规武器对地下工程目标毁伤实验数据的特点，建立了基于马氏距离的数据异常检测算法，实现了对源数据的甄别、分析和清洗，提高了数据挖掘计算结果的可靠性；

（2）针对毁伤效应控制因素多、精确匹配检索数据困难的情况，采用相似搜索技术检索高维空间中与预测输入向量相似的实验源数据，提高了实验数据匹配率，保证了充分优先利用大量的真实实验数据，提高预测精度；

（3）建立了地下工程目标毁伤效应分析的“三阶段”算法，利用实验数据、工程算法和神经网络模型进行毁伤效应计算，特别是在缺少工程算法的情况下，“三阶段”算法可利用现有实验数据建立神经网络模型进行计算，从而实现基于实验数据驱动的毁伤效应分析。