基于遗传算法的轮辋放气装置优化分析
吴中元 何子燚 黄永博
中汽研汽车检验中心(武汉)有限公司 湖北武汉 430056
1 前言
汽车已经成为人们生产生活中不可缺少的工具,在为人们带来方便和迅捷的同时,也会给人们造成生命和财产的巨大损失。据统计显示,近年来我国高速公路安全事故中,爆胎事故占65%以上[1],事故死亡人数占总数的49.81%,受伤人数占63.94%,直接财产损失占总损失的43.38%[2]。显而易见,汽车爆胎是道路交通事故的头号杀手!怎样最大限度地减少由于轮胎爆胎而引发的交通事故,尤其是防范由此引发的群死群伤事故,已经引起社会各界的关注。因此,爆胎应急安全技术研究成为了国内外的共同课题。现阶段的爆胎道路试验,常用的爆胎方法有枪击法、炸药爆破法和轮辋放气法等。枪击法和炸药爆破法的实验材料受到国家严格的管控,获取困难,同时也存在不安全性和重复性差等问题;轮辋放气法重复性好、爆胎效果理想,可是密封要求高,需要对每种型号的轮辋制作特定的放气装置而成本高、周期长。针对以往模拟汽车爆胎试验存在的不足,以放气时间为研究对象,通过构建压力与时间关系模型,找到该装置下放气时间最短的最优方案(放气口径、数量),达到放气时间短、爆胎效果好、成本较低的效果。
2 轮辋放气装置结构及特性分析
爆胎应急安全装置,是汽车的一项被动安全产品。它能有效在车辆发生爆胎瞬间,避免轮毂与地面接触,使车辆转向力及制动力仍然可控的行驶一段距离,第一时间保证人员及车辆安全。爆胎应急安全装置安装在车轮轮槽部位,主要由支撑圆环、弹性钢带和锁紧机构组成,其结构如图1所示。

图1 爆胎应急安全装置结构图
由于车辆爆胎是瞬间释放轮胎内的气体,过程非常迅速。为此,研究远程控制模拟爆胎装置具有重大意义。模拟爆胎时对装置性能要求很高,具有不漏气、定时定点及远程操控放气等特点。为此,开发了一套气缸式快速放气装置。该装置由支管轮毂、过渡储气室、执行构件和控制模块四部分组成。支管轮毂是为释放轮胎气体的输出口,由多个折弯支管与轮辋焊接引出,其在轮辋上的破口即为轮辋轮槽一圈部位;过渡储气室是一种导环与圆柱缸体通过直线滑动形成的气密滑轨,其圆柱体外壁一圈引出多个破口,外壁破口与支管轮毂引出的折弯支管通过气密管路连接形成密闭回路;执行构件为轮胎放气的先导部件,由气缸和导环构成,导环与气缸活塞杆连接,使导环能在过渡储气室中快速进退;控制模块由电磁阀及无线模块组成,电磁阀控制气缸的进退动作,无线模块主导电磁阀的换向动作,进而控制气缸进退功能。
轮辋放气装置在工作前,先把过渡储气室中导环压入圆柱缸体中,使轮胎、支管轮辋和过渡储气室形成一个密闭气室。此时,控制模块中的电磁阀进气路与气缸中上腔连通,从而形成装置内气体使过渡储气室中导环处于平衡状态。一旦模拟爆胎时,控制模块给电磁阀信号,其阀体立刻换向,从而控制模块中的电磁阀进气路与气缸下腔连通,气缸上腔连通大气,进而过渡储气室中的导环上下产生压力差,加速推进导环开启,快速实现轮胎放气,轮辋放气装置结构特性,如图2所示。
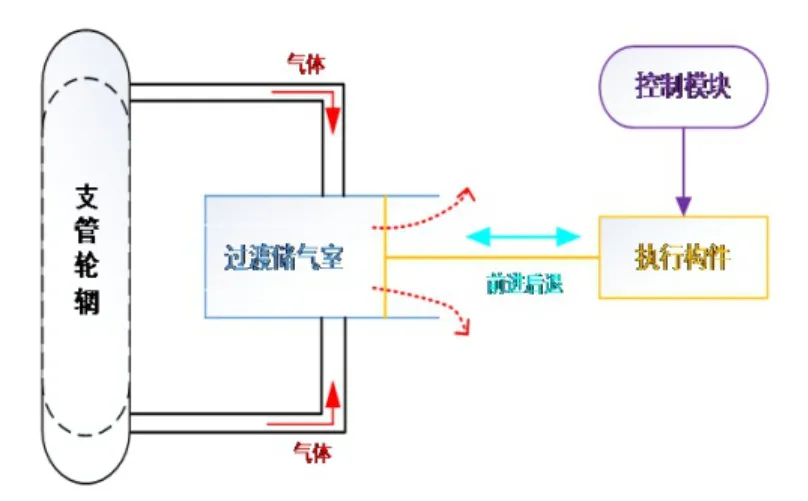
图2 轮辋放气装置结构特性图
依据轮辋放气装置的结构特点,影响其放气快慢的因素主要有支管轮辋和过渡储气室的管路长度、数量及直径,过渡储气室导环截面积,过渡储气室中导环与圆柱缸体的滑移装配性,气缸的缸径,控制模块与气缸连接的管路直径等因素,其影响因素如图3所示。

图3 放气时间影响因素
由于支管轮辋和过渡储气室中管的弯曲折叠易造成管路堵塞,以及安装空间有限,因此安装后选择最短的管路为宜;过渡储气室中导环与圆柱缸体的滑移装配是整个装置密封的难控点,因为气体密封在刚性部件间需添加橡胶垫圈,在此期间,橡胶垫圈的材料对放气快慢起到一定的阻碍作用,但影响不大;当控制模块输出信号电磁阀换向时,电磁阀进气路与气缸下腔连通,气缸的向上推力可直接影响轮胎气体从过渡储气室中释放的进程;当然,气缸上腔连接的管路中气体的释放快慢对过渡储气室中导环滑移有一定的影响,间接影响放气时间;主要影响轮胎放气快慢的因素是管路的有效截面积和过渡储气室导环截面积,但在实际试验中,由于管路弯曲变形及堵塞等原因,很难获取管路的有效截面积。
3 轮辋放气装置的放气规律研究
由于神经网络拥有很强的非线性拟合能力,可映射任意复杂的非线性关系,并且学习规则简单,鲁棒性好及自学能力强等特点。因此,使用神经网络拟合放气时间与因素之间的关系,可得出一种基于神经网络的放气规律模型。若对放气时间影响较大则作为实验因素,否则作为干扰因素。当选好实验因素后,开始制定实验方案并采集数据;实验完成后,运用统计软件对实验数据进行统计分析,拟合出放气规律的模型;最后,进行模型验证;其放气规律模型流程图如图4所示。
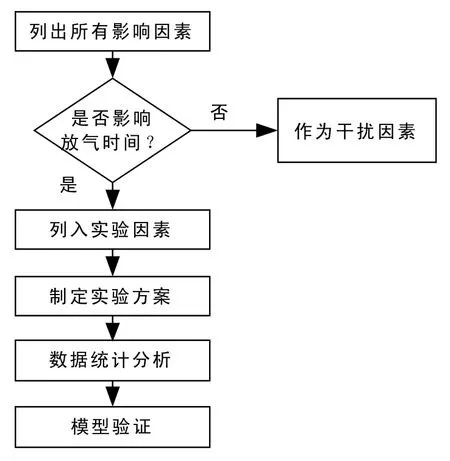
图4 放气规律模型流程图
经过对图5的分析,为了能够使用神经网络数据拟合,该实验中选取了3个因素,压差、管路数量n及直径d,其影响因素及其水平的选择和取值如表1所示。

表1 影响因素及因素水平
具体实验流程总结如下:
a.根据正交实验表 27L,设计三因素三水平的实验设计方案如表1所示;
b.检查模拟爆胎装置气密性,确保正常工作的状态,然后开始执行实验,当轮胎气压很低时(低于0.1MPa,接近大气压),放气时间非常缓慢,此时不计入放气时间;
c.试验中,每0.01s采集一次,同时将实验数据保存于计算机当中,为下一步的数据分析做准备;
d.重新调整实验参数,重复步骤2和步骤3。
通过采集的数据结合神经网络,利用MATLAB分析,得出BP网络预测输出及BP网络预测误差如图5、6所示。
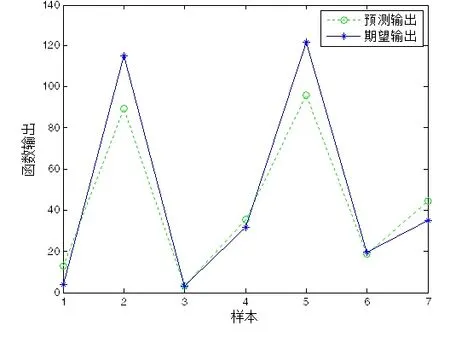
图5 BP网络预测输出图

图6 BP网络预测误差图
最后得出神经网络放气时间规律模型为:

4 基于遗传算法的放气时间优化分析
遗传算法(GA)是一种进化算法,其基本原理是仿效自然界中的生物进化论,通过仿效生物界自然选择过程中的演化法则而发展形成的多路径全局优化算法[4]。基于神经网络的放气规律模型只能用于各种影响因素下放气时间的预测。在实际试验中,为了保证放气时长最短,往往使用遗传算法对放气时间影响因素进行全局优化,找出最短的放气时间下影响因素组合。主要步骤为:首先采用二进制编码初始化和创建种群,然后对神经网络放气时间预测模型进行计算,再计算每个个体的适应度值,当达到设定的结束条件时,就把适应度值最大的个体作为最优结果并解码输出,否则就继续遗传操作直到满足结束条件为止。本文设置的结束条件为种群的进化代数,最短放气时间为优化目标。
4.1 参数优化的确定
由于放气时间中影响参数众多,若只针对某一个参数进行优化,则可能达不到理想优化的效果。因此,需要根据优化的目标对各个参数的类型和优化的可能性进行判断。由建立的放气时间预测模型可知,影响放气时间的参数主要有压差、管路数量及直径。其参数的约束主要分为以下4个方面。
4.1.1 管路数量约束nmin≤n≤nmax
由于轮辋结构及模拟爆胎装置安装空间限制,其管路数量nmin=1,为使放气时间越快越好,管路数量nmax=30,更多则无法安装。
4.1.2 管路直径约束dmin≤d≤dmax
为使放气时间最短,则要求数量多、直径大的管路,结合轮辋安装在鼓式制动器上。由于空间特别有限,将依据实际经验确定管路直径。此处开孔直径dmax=10 mm,若直径特别小的话,无实际意义。因此约束dmin=6 mm。
4.1.3 压差Dpmin≤Dp≤Dpmax
正常载货汽车轮胎气压约为900 kPa,当出现爆胎时,由于大气压远小于轮胎气压,导致气体快速放出,因此取Dpmin=700 kPa,Dpmax=900 kPa。
4.1.4 目标函数

式中,T(x)为放气时间的函数;
x为待优化变量,la和ua分别为变量x的下限和上限约束。
4.2 放气时间的优化模型
通过确定参数优化变量的约束条件、优化目标函数,可以将放气时间进行优化。模型归结为一个单目标三变量的模型。
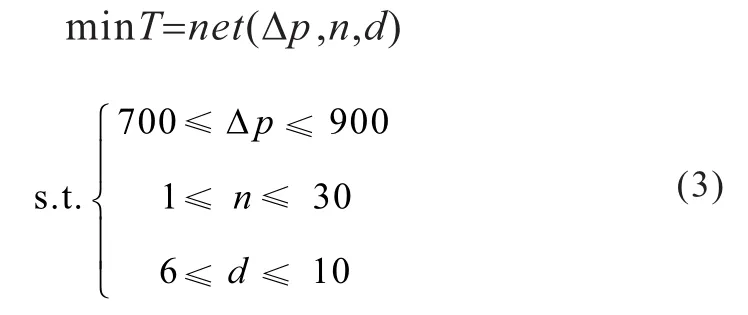
5 案例分析
本节使用MATLAB仿真分析,具体步骤如下:
a.将压差、管路数量及直径作为优化的变量,根据式(3)中的取值范围随机产生50组二进制数据构成遗传算法的初始种群。
b.适应度越大,解的质量越好,由于求解最小化T(x)的参数值,因此将T(x)作为算法的适应度函数,并计算出所有个体的适应度值。
c.采用轮盘赌的方式选择适应度值较大的个体。以单点交叉的方法对选择操作后的新群体进行交叉操作,定义交叉概率为0.05,变异概率为0.9。
d.将迭代次数设置为100代,作为算法的终止准则。当迭代次数超过100时,则停止计算,得到最优参数解。
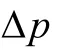
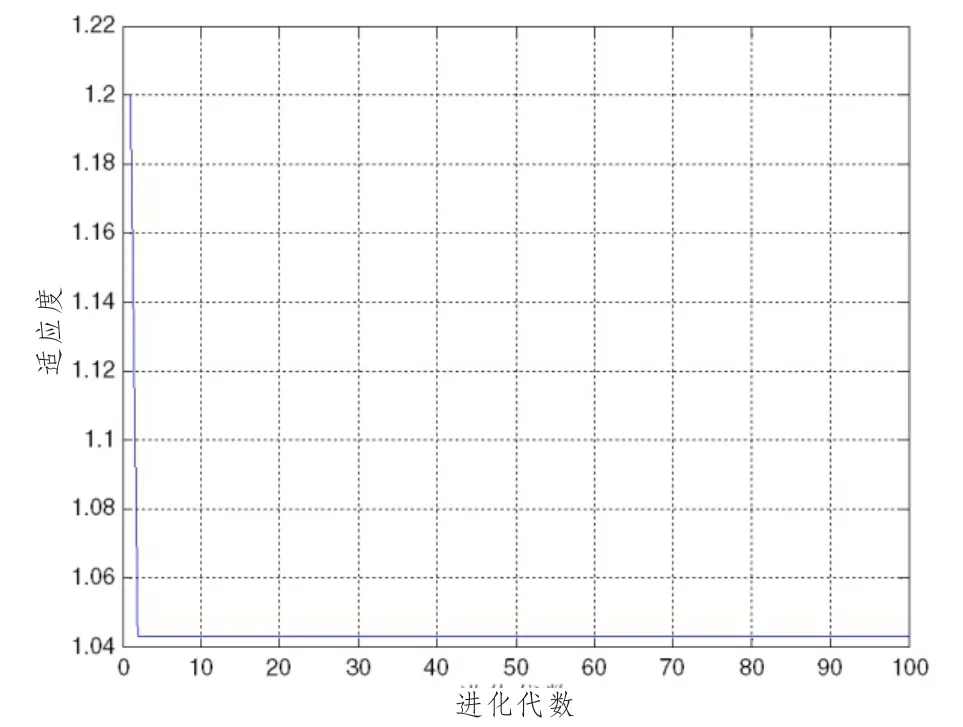
图7 放气时间与进化代数的关系图
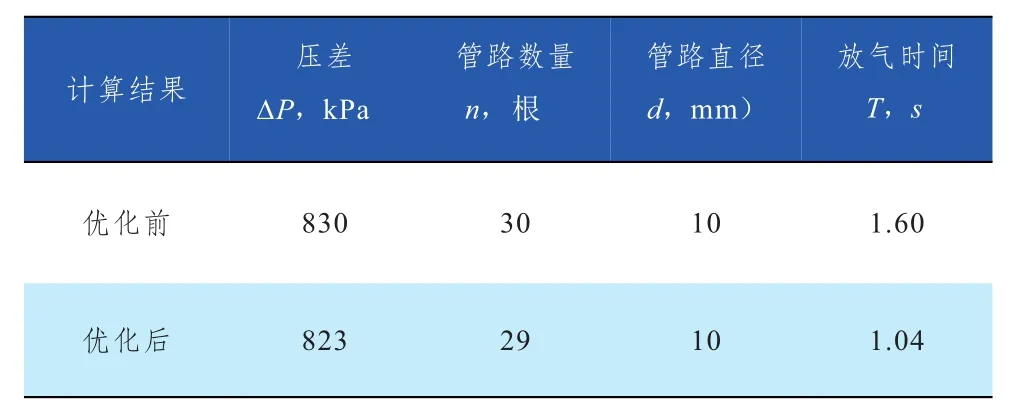
表2 优化前后结果对比分析
6 总结
本文以压差、管路数量及直径作为优化的变量,建立基于快速放气装置的神经网络放气时间预测模型,并利用遗传算法进行了优化计算。模拟放气时间实例优化分析表明,优化获得的放气时间比优化前降低35%。本文可为爆胎模拟装置提供一种理论方法支持、助于优化爆胎模拟装置结构。在建模中,试验数据为模拟爆胎静态数据,在动态试验中会受到路面、车况以及人的反应等因素与放气时间的关系模型尚需进一步研究。

