基于车辆自动定位数据的有轨电车运行效率分析与应用*

蔡国涛 冯远通 刘舒婕

(1. 深圳市现代有轨电车有限公司， 518109， 深圳；2. 上海市轨道交通结构耐久与系统安全重点实验室， 201804， 上海∥第一作者， 工程师)

运行效率是评价有轨电车系统服务质量的重要指标。文献[1]在阐述有轨电车系统构成的基础上，分析其技术适用性，提出了相应的技术适用条件，归纳总结出适用于不同城市的5种应用模式及相应的合理线路长度，并以模糊综合评价模型为基础，运用层次分析法对有轨电车的区域适用性进行了综合评价。文献[2]的研究也显示出有轨电车系统的可靠性对有轨电车线路运行有不可忽视的影响。

有轨电车的运行特性在一定程度上与道路公交的运行特性相似。因此，参考道路公交的研究具有重要意义。文献[3]基于AVL(车辆自动定位)数据，定量分析了道路公交的运行可靠性及其相关关系。文献[4]使用深度神经网络模型来实现公交到达时间的预测，并量化了不同因素的联合影响。

本文结合AVL数据结构对有轨电车运行效率影响因素进行分析，并对有轨电车运行效率指标作细致的量化，然后结合已运营有轨电车线路的真实数据，将其线网模型的评估算法应用到实际算例中。

1 有轨电车AVL数据及运行效率影响因素

1.1 AVL系统与数据预处理

有轨电车AVL系统是一种基于计算机技术的车辆追踪系统，不仅能实时提供有轨电车运行的时空位置信息，也是报站系统、车辆动态监控系统、智能调度系统等运行的重要基础[5]。

本文针对有轨电车数据的结构和内容，提出面向AVL数据的预处理方法，内容包括对重复数据、缺失数据和异常数据的清洗，以及对多源数据信息的关联与合并。AVL数据的预处理流程见图1。

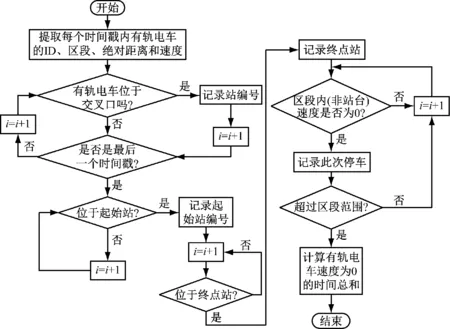
注：ID——起讫点。

1.2 有轨电车线路运行效率的影响因素

有轨电车系统是人、车、线路及环境相互作用的复杂系统。本文将运行效率影响因素归为车站、路段、交叉口3类。其中：车站是有轨电车线路上供车辆到发、通过和折返等作业的分界点，有轨电车需要在车站办理停车作业；交叉口是有轨电车线路在道路信号控制影响下形成的特殊分界点，有轨电车可能需要在交叉口停车等待绿灯通行；路段是车站与车站、车站与交叉口之间连接的主要通道。对车站、交叉口和路段这3个要素进行分析，是构建有轨电车线路运行效率评价模型的基础[6]。

1) 车站。有轨电车车站按布设型式可分为侧式、岛式、岛侧混合式。其中：侧式站台设置在上下行线路的两侧；岛式站台设置在上下行线路之间；混合式站台通常用于换乘站。根据站台位于交叉口进出口道的位置，有轨电车车站还可分为进口道站台和出口道站台。应结合每个车站的实际情况进行有轨电车的线路设计，同时充分利用有轨电车的灵活性和多样性，最大限度地发挥其优势。

2) 交叉口。与传统的城市轨道交通线路不同，有轨电车一般运行在城市的地面道路上，因而在通过道路平交交叉口时会受到道路交叉口信号控制系统的影响，需要根据交叉口信号指示决定车辆通行或停车等待。交通统计数据表明，有轨电车运行延误的80%来自于交叉口的停车等待。交叉口限制了有轨电车的行车效率，使得有轨电车的运行速度较低，从而影响了有轨电车的服务质量。

3) 路段。有轨电车根据进路的排列依次经过相应的路段和分界点，路段长度决定了有轨电车到达、离开各分界点的时间。此外，路段长度会在一定程度上影响有轨电车的加速度曲线。

2 路段运行效率分析模型

本文通过构建多元线性回归模型，重点从基础设施和控制策略2方面对有轨电车线路的运行效率进行分析，并研究线路条件、站台属性、控制策略等关键参数对有轨电车运行效率的影响。

2.1 变量定义

将2个车站之间的线路定义为一个路段。为定量分析各因素对有轨电车运行效率的影响，对各因素的量化说明如表1所示。

表1 有轨电车运行效率模型的变量定义

2.2 多元线性回归分析

由上述分析可知，有轨电车系统的运行效率受多种因素影响。为解释各因素影响有轨电车运行效率的机理，应对单因素进行逐一分析。

1) 站台位置。为了评估不同站台位置对有轨电车平均运行速度的影响，选取某有轨电车线路某区段的上下行方向进行对比。该区段的上、下行方向站台位置分别位于交叉口的出口道、进口道。对比有轨电车经过该区段时的平均运行速度，结果如图2所示。从图2可以看出，有轨电车驶入出口道站台时，平均运行速度较高。

2) 路段长度。为了评估不同长度路段对有轨电车运行效率的影响，选取某有轨电车线路上若干个路段，对比有轨电车在该路段的平均速度(见图3)。可见，随着路段长度的增加，有轨电车在路段上的平均运行速度也随之变大。但是，当路段长度在400～700 m区间时，有轨电车的平均运行速度差异并不大。

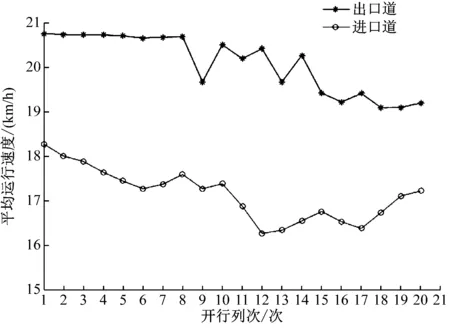
图2 不同站台位置下的平均运行速度对比

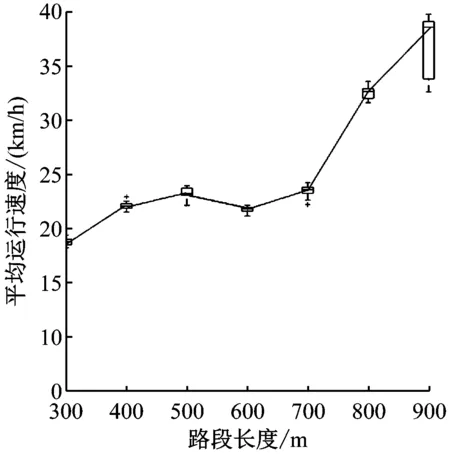
图3 不同路段长度下的平均运行速度对比

3) 交叉口。为了研究道路交叉口交通控制策略对有轨电车停车延误造成的影响，选取包含交叉口的某一区间，对不同运营趟次的有轨电车在该区间的速度曲线进行对比分析，如图4所示。由图4可以看出，有轨电车在交叉口因信号控制而造成的停车延误对运行效率造成较大影响。

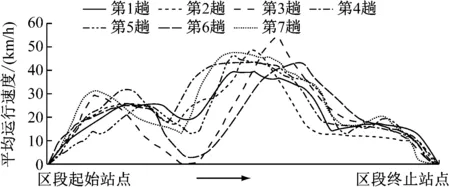
图4 不同运营趟次在某交叉口路段的速度对比

2.3 建立多元线性回归模型

由于评价有轨电车运行效率的自变量有多个指标，而因变量只有路段运行时间均值1个指标，所以本文建立的多元线性回归模型公式如下：

yi=β0+β1x1+β2x2+…+βkxk+ε

(1)

式中：

yi——路段i的运行时间均值；

β0——常数项；

xk——自变量(具体含义见表1)；

βk——xk对应的系数；

ε——随机误差项。

2.4 实例分析

2.4.1 实例描述

图5为选取的有轨电车线网案例。其中，黑色部分为已开通运营的T1线。

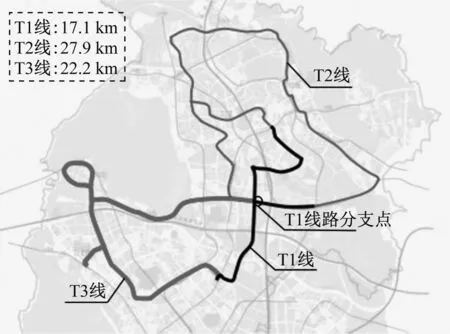
图5 有轨电车算例线网图

2.4.2 多元线性回归模型的结果分析

为表明回归方程的显著性，利用统计软件Matlab对求解得到的多元线性回归模型进行了显著性检验。经计算，因变量yi预测值与路段实际运行时间均值调整后的复测定系数为0.954,说明自变量能解释因变量yi的95.8%，而剩余的4.2%要由其他因素解释。该模型的样本量为310个，其回归结果统计如表2所示。

表2 有轨电车运行效率多元线性回归模型的统计结果

本文对选定指标与路段运行时间均值进行回归分析，最终得到回归方程如式(2)所示。

y=-105.9x1+117.7x2+90.5x3-52.2x4+

0.26x5-0.07x6+119.4x7-0.46x8

(2)

式中：

y——列车在路段内的运行时间。

结果表明，有轨电车的路段运行时间随着交叉口个数的增加而增加。同时，当车站位于出口道时，路段行程时间将略有减少。此外，与经停侧式站台的路段运行效率相比，有轨电车经停岛式站台的路段运行效率较高。路段长度对平均运行速度也有直接的影响，这是由于有轨电车的启动和停车都会极大地影响其在单个路段中的运行效率。而交通量、周期时长及绿信比等交叉口相关影响因素能在一定程度上表征不同交叉口对于有轨电车相位的优先策略。结合以上的数据分析结果，能够更好地拟合有轨电车过交叉口时的运行情况。

3 模型在新建线路运行效果预测及优化建议

3.1 在新建线路中的运行效果预测

该模型还可用于预测新建T3线的运行效率。如表3所示，该线全长为7 607 m，基于T3线的基础设施物理参数及信号配时参数，预测得到各路段的运行时间和平均运行速度。在此基础上计算得到该线单程的运行时间(1 309.94 s)和平均运行速度(20.91 km/h)。表3中的交叉口型式、站台位置、站台型式的取值含义见表1。

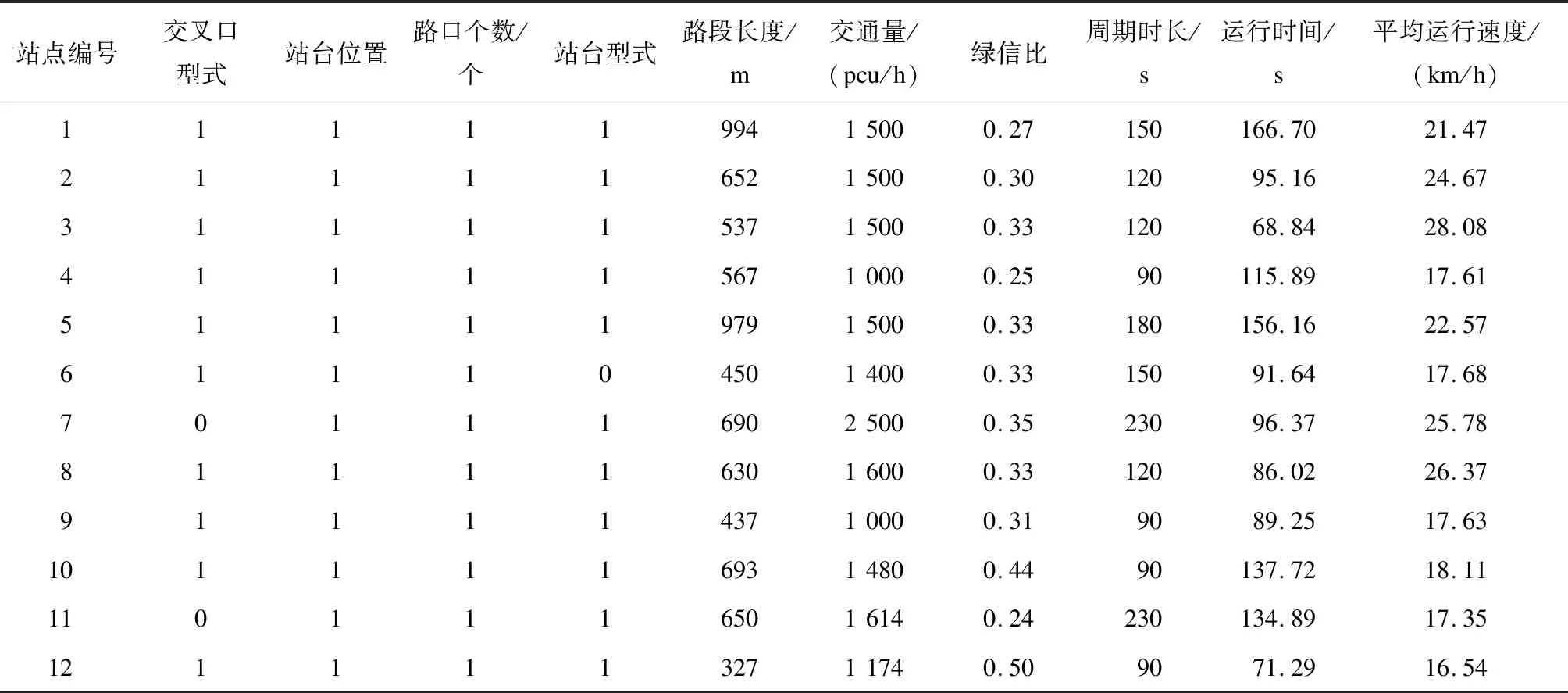
表3 有轨电车T3线的运行情况预测

通过模型拟合得出以下结论：① 在有轨电车绝对优先的情况下，预测T3线全线平均运行速度可以达到24.40 km/h；② 通过现有数据拟合，考虑有轨电车在交叉口受信号控制影响情况，预测T3线全线平均运行速度可以达到20.91 km/h。

3.2 优化建议

1) 可从建设根源上改善有轨电车运行效率，如合理地规划站间距离、设计站台型式及位置等。

2) 可通过优化信号控制策略来改善有轨电车运行效率。

3) 可以通过鼓励出行者错峰出行来缓解高峰时段有轨电车在交叉口运行的压力。同时，针对机动车与非机动车混行通过交叉口问题，可在交叉口渠化上做进一步的优化。

4) 应结合实际运营数据，优化仿真算法，制定调整改善措施，进一步提高运行效率和服务质量。