不完全CSI下协作空间调制系统中继选择及分析*

李 彤，仇润鹤

（1.东华大学，上海 201620；2.数字化纺织服装技术教育部工程研究中心，上海 201620）

0 引言

随着通信技术的发展，多输入多输出（(Multiple Input Multiple Output，MIMO）技术由于其可以成倍地提高系统的吞吐量和频谱效率，因此在现代无线移动通信中得到了广泛的应用。它的基本原理是充分利用频谱资源，在源节点和目的节点间配有多根天线进行发送和接收。但是多根天线的应用在提高通信质量的同时，也带来了一些不足，如信道间同步，天线间干扰等[1]。因此在MIMO技术的基础上，又提出了一种被称为空间调制（Spatial Modulation，SM）[2]的多天线技术，其每时隙仅激活一根发送天线，有效避免了信道和天线间的干扰、同步等问题。并且由于其在射频链路、接收天线数目等方面的要求没有MIMO严格，因此在被提出后即受到广泛关注和研究，并延伸出正交空间调制（Quadrature Spatial Modulation，QSM）、空间移位键控（Space Shift Keying，SSK）等技术。协作通信作为一种虚拟的MIMO技术，将中继节点应用于通信系统中，通过在目的节点收到来自不同链路所传输的相同信号的副本进行合并和检测，最终恢复出原发送信号，在提高系统分集增益的同时也能够加强传输的可靠性。现在常用的中继传输协议有放大转发协议（Amplify-Forward，AF）、解码转发协议（Decode-Forward，DF）、机会中继等。将SM相关技术与协作通信技术相结合，不仅可以解决传统MIMO系统的不足，而且能提高通信系统的传输可靠性，获得更高的分集增益。

现有采用多个放大转发中继协作空间调制系统中，若想对全部中继进行选择，大多是采用随机选择转发或全部中继循环转发等，如文献[3]分析了多中继SSK系统的误比特率性能，当系统中的中继为AF中继时，所有中继全部循环转发；文献[4]分析了多中继时QSM系统的误码性能，该系统中使用源节点中的一部分发送比特来随机选择中继序号。但这些方法在选择中继时大多没有考虑到当中继位于系统不同位置时的情况；且在实际通信过程中，目的节点对接收到的来自不同链路的信号进行合并检测，由于信道的不稳定性和信道状态信息的不完全估计，实际的信道状态信息与估计值之间会存在一定的误差，因此需要考虑不完全信道状态信息（Channel State Information，CSI）对系统性能的影响。文献[5]研究了完全和不完全CSI下上行大规模多用户空间调制系统的误码性能和频谱效率。文献[6-7]分析了不完全CSI下SM和SSK系统在α-μ、κ-μ和η-μ衰落信道下的成对错误概率。文献[8]分析了不完全CSI对QSM系统误码性能的影响。在协作中继与空间调制相结合的系统中，若考虑信道估计误差的影响，对系统的分析将更加符合真实情况。文献[9]将空间调制用于解码转发认知无线电系统中，分析了系统的平均成对错误概率，并研究了信道估计误差的影响。文献[10]在已知完全信道状态信息的基础上分析了当不完全信道估计时协作空间调制系统的误比特率，当信道估计误差为0时，分析结果与完全估计时相同。文献[11]分析了存在信道估计误差时采用单个AF中继的SM系统误比特率；文献[12]在文献[11]的基础上对该系统进行了功率分配，能够进一步降低系统的误比特率，提高传输的可靠性。但以上文献尚未在不完全CSI下将空间调制与多中继协作通信联合考虑进行分析。

由此，本文将空间调制、中继选择与不完全CSI相结合，提出了一种基于中继位置信息对全部中继进行选择的方案LRS（Location-based Relay Selection，LRS），并研究了信道估计误差对协作空间调制系统误比特率的影响。文中首先经过理论分析，得出使得接收端信噪比最大的最优中继位置，据此给出了具体的中继选择方案，并将其应用于不完全CSI情况下的协作空间调制系统中；针对系统中目的节点使用最大似然检测（Maximum Likelihood，ML）解调出的信号，分析了系统的理论平均误比特率和高信噪比下的渐进误比特率，以及两种不同信道估计误差对系统误比特率的影响。

1 系统模型

考虑一个如图1所示的将空间调制与协作通信相结合的系统，称之为AF-SM系统。图中R表示中继节点。该系统模型由源节点、中继节点和目的节点组成，其中源节点配有Nt根发送天线，目的节点配有Nr根接收天线，中继配有根发送天线和根接收天线，且为降低系统复杂性，令在源节点采用了空间调制技术，将发送比特分为选择天线序号和调制信号两部分。该系统共有两条链路，分别为源节点发送数据不经中继转发直接传递给目的节点的直接链路S-D，以及源节点发送的数据经过中继放大后再转发给目的节点的中继协作链路S-R-D。各节点之间均服从独立的平坦瑞利衰落信道，信道系数矩阵分别为hsd、，i表示所选择的中继序号，矩阵中元素均服从均值为0，方差为δmn2的复高斯分布，且各节点间均存在服从CN(0,N0)分布的噪声nmn，式中m、n∈{S,R,D}。

图1 AF-SM系统模型

源节点所使用的空间调制技术是一种能够解决传统MIMO系统同步等问题的新的多天线传输方案。在空间调制系统中，将源节点准备传输的信息比特分为两部分，一部分用于对信号进行传统的M进制调制，如M-PSK、M-QAM等；另一部分用于选择天线序号，并将调制好的信号经过所选择的天线进行传输，每一时隙仅激活一根天线，能够有效避免多根天线同时传输时所产生的天线间同步、干扰等问题。因此，每一时隙源节点所发送的信号矢量xlq可以表示为：

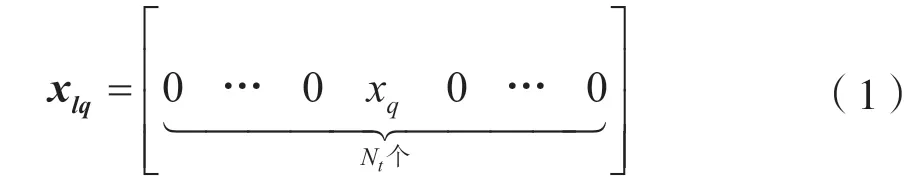
其中唯一非零元素xq为经过M进制调制的一个星座点，为该矢量中第l个元素，l为选择的天线序号。调制阶数M和发送天线数目Nt共同决定了每时隙发送的总比特数B：

1.1 系统传输方案

目的节点接收到的信号ysd和被选择的第i个中继接收到的信号为：

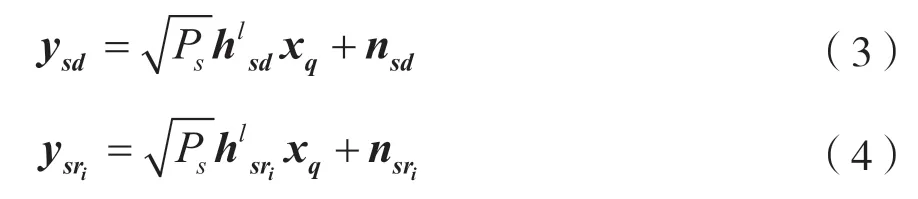
式中，Ps为源节点发射功率，分别表示源节点和目的节点之间以及源节点和被选中的中继之间的信道矩阵的第l列，xq为经过调制后的信号。nsd和分别表示源节点与目的节点和中继间的信道噪声。

被选择的中继节点在接收到来自源节点的信号后，会将该信号进行放大并转发给目的节点，目的节点接收信号为：

考虑到信道估计误差的存在，实际信道系数和它的估计值之间有如下关系：于信道估计误差矩阵中元素的方差考虑两种情况：①其为与信噪比无关的固定值；②其为随信噪比增大而减小的减函数。

因此根据式（6）的信道估计模型，当考虑信道估计误差时，可将式（3）改写为：

在目的节点对接收到的信号进行基于最大似然的最优检测后，恢复出所选择的天线序号和调制信号为：

1.2 LRS中继选择方法

考虑到多个中继节点可能处于源节点和目的节点间不同的位置，该位置信息可能会对系统的性能产生影响，且多个中继进行协作时，需要考虑功率分配、同步等问题，也增加了系统的复杂度，因此采用单中继协作方案，选择出最接近最优中继位置的次优中继进行放大转发。为了使接收端信噪比最大化，提出了基于中继位置信息对全部中继进行选择的LRS中继选择方法。该方法假设各节点的位置信息已由现有定位技术得知。

文献[14]引入了等效信道增益，对全部中继的等效信道增益进行降序排列，选择增益最大的中继节点进行转发。基于此，根据对数-距离的路径损耗模型[15]，给出本系统中信道增益为：

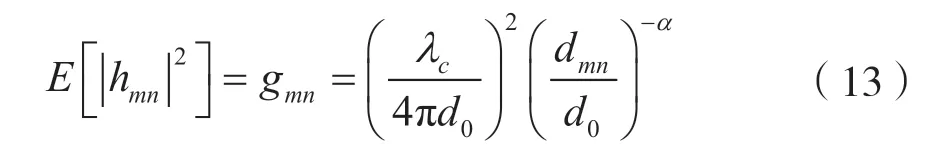
式中，λc为载波长度，dmn为m、n节点间距离，d0为参考距离，α为路径损耗因子，一般取3～5，m、n表示系统中各节点，即S、R或D。已知目的节点对源节点和中继传输来的数据进行合并后的接收端信噪比为：

因此，接收端信噪比同样可简化为：

在高信噪比下，等功率分配时，对上式求平均，得：

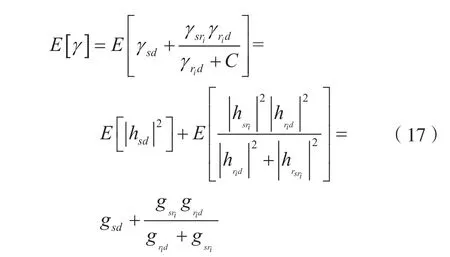
将式（13）的信道增益带入上式后得到[17]：

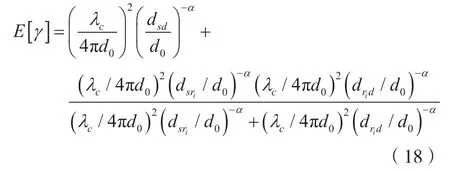
因为源节点和目的节点间距离固定，即dsd不变，对上式进行化简后，可得：

由上述可以证出，使得接收端信噪比最大的中继位置应该位于源节点和目的节点间中点位置。故所提出的LRS中继选择方法即为从全部中继中选择出最接近源节点和目的节点间中点位置的次优中继。该方法可简单描述如下，其中假设中继位于源节点和目的节点之间，且全部节点已知自身的位置信息

（2）令一距离矩阵为d，并将步骤（1）中所计算的全部中继的差值存储于该距离矩阵，即有

（3）行矩阵中的最小值即表示该中继位置最接近源节点和目的节点间的中点，因此应该选择该中继进行放大转发，此时所选择的中继序号应为

式中，R为所选择的中继序号，n为中继数量。

2 性能分析

2.1 误比特率分析

本节对所提出的LRS中继选择方法应用于协作空间调制系统且进行误比特率的分析，考虑了信道估计误差存在的情况。使用矩生成函数法得到了该系统成对错误概率（Pairwise Error Probability，PEP）的解，给出了系统误比特率（Average Bit Error Probability，ABEP）的上界，并基于此给出了高信噪比下的渐近误比特率。

假设在源节点所选择的天线序号和调制的信号可表示为λ(l,xq)，在目的节点所解调出的天线序号和调制信号表示为其中可由式（12）得出，因此可以给出条件PEP为：

故系统的PEP可以表示为[18]：

式中E[·]表示期望，分别为两条链路瞬时信噪比的矩生成函数。令式（22）中t=sinθ，且被积函数为偶函数，则可化简为：

由高斯-切比雪夫求积公式[16]，可以求出上式积分解的表达式为：

因此，该AF-SM系统的PEP可以通过分析所提出系统中两条链路S-D和S-R-D的瞬时信噪比的矩生成函数来得出。接下来将分别求解这两个矩生成函数

2.1.1 S-D链路瞬时信噪比的矩生成函数

又矩生成函数是概率密度函数的拉普拉斯变换，因此对（24）式进行拉式变换，可得该链路瞬时信噪比的矩生成函数为：

2.1.2 S-R-D链路瞬时信噪比的矩生成函数

式中，Kv(·)为第v阶贝塞尔函数。

由于M(s)=sL[F(γ)]，对式（32）进行拉普拉斯变换，并由文献[19]中(6.643.3)，令，可以得出S-R-D链路的矩生成函数为：

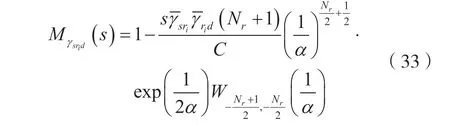
式中，Wa,b(·)为惠塔克函数。

将式（27）和式（33）所求得的各链路瞬时信噪比的矩生成函数带入式（24），即可求得在不完全CSI下的AF-SM系统PEP的解为：

式中：

因此，代入以下理论平均误比特率的统一上界，即有：

2.2 渐近误比特率分析

基于以上对理论误比特率的分析结果，为了能够更加深入地了解系统的性能，在本节中对该系统的渐近性能进行简要分析，并在假设系统接收天线数目Nr=1的情况下推导出了高信噪比下的渐近表达式。

由式（21）已得系统的PEP为：

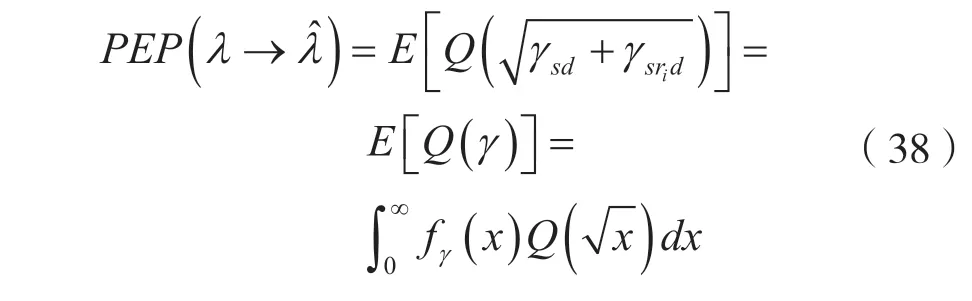
式中，接收端信噪比的概率密度函数fγ(x)为：

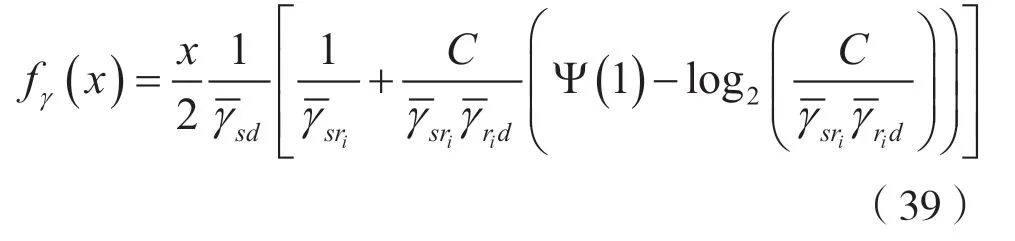
式中，Ψ(·)为Digamma函数，即伽玛函数Γ(·)的对数导数。将式（39）带入式（38）的PEP中，可得该系统的渐近PEP为：

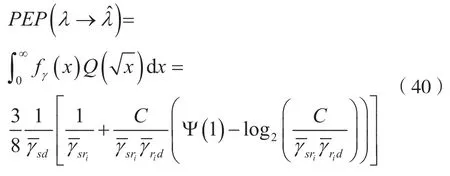
为了研究信道估计误差对整个系统误比特率的影响，接下来将分别考虑3种信道估计误差时系统的渐近PEP表达式。

将以上分析得到的PEP分别带入式（37）中，可得不同信道估计误差下的系统理论误比特率的上界表达式。

3 仿真结果与分析

使用MATLAB对提出的在不完全CSI下的AF-SM系统的误码性能进行仿真验证与分析。在仿真中，使用瑞利衰落信道，信道状态信息存在估计误差，源节点和目的节点间距离规定为1，中继均匀分布于两点之间所在直线上。假设各链路估计误差的方差均相等，源节点发射天线数目Nt=2，目的节点接收天线数目Nr=2、4，中继发射天线数目和接收天线数目调制方式为BPSK和QPSK，中继数量为0、1、4个，信道间衰落系数α=5。

图2给出了目的节点接收天线数目Nr为2，使用QPSK调制，当估计误差的方差为不随着信噪比的变化而变化的固定值时绘制AF-SM系统的误比特率比较曲线，实线表示仿真结果，虚线表示理论误码率。图中曲线的标记符号分别表示估计误差的方差σe2为0.1、0.01、0.001和完全估计（σe2=0）。从图中可以看出，在不完全CSI的系统中，当σe2为0.1时，误比特率最高；当σe2为0.001时，误比特率最低。系统的误比特率随着估计误差的方差减小而减小。当理想情况估计误差的方差为0时，即完全估计的情况下，系统的误比特率最低。从图中还可以看出，当估计误差的方差为固定值时，系统的误比特率曲线随着信噪比的增大而逐渐平缓，最终将趋于常数，此时增加信噪比已经不能有效改善系统的误码性能。

图3给出了目的节点接收天线数目Nr为2，使用QPSK调制，当估计误差的方差为随着信噪比增大而减小的减函数时AF-SM系统的误比特率比较曲线。图中标记符号也分别表示了估计误差的方差分别为1/(P/N0)、1/(2(P/N0))、1/(3(P/N0))和完全估计（σe2=0）。从图中可以看出，所提出的AF-SM系统存在估计误差，且其方差为1/(P/N0)时，误比特率最高；方差为1/(3(P/N0))时，误比特率最低。系统的误比特率随着估计误差的方差减小而降低，在已知完全信道状态信息的理想情况下，系统的误比特率达到最低。

图2 估计误差的方差为固定值

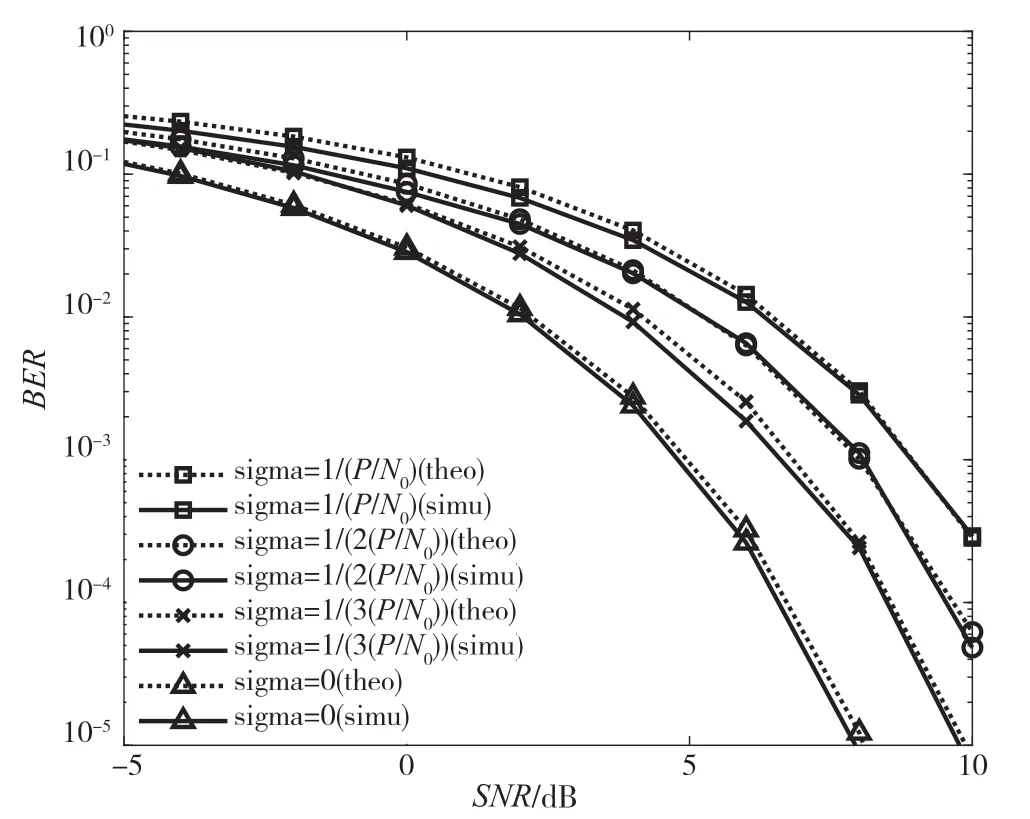
图3 估计误差的方差为可变值

图4给出了目的节点接收天线数目Nr为2，使用QPSK调制，当估计误差的方差为随着信噪比增大而减小的减函数1/(3(P/N0))时，采用不同的中继选择方法对系统误比特率的影响。在文献[3-4]中，当存在多个放大转发中继时，使用随机选择中继转发、循环转发的方式对中继进行选择，将本文AF-SM系统所使用的方法与以上两种方法进行对比，即使是存在信道估计误差的情况下，提出的选择最接近源节点和目的节点间中点的中继的方法与随机转发、循环转发的方式相比，在降低误码率方面也有一定的提升。

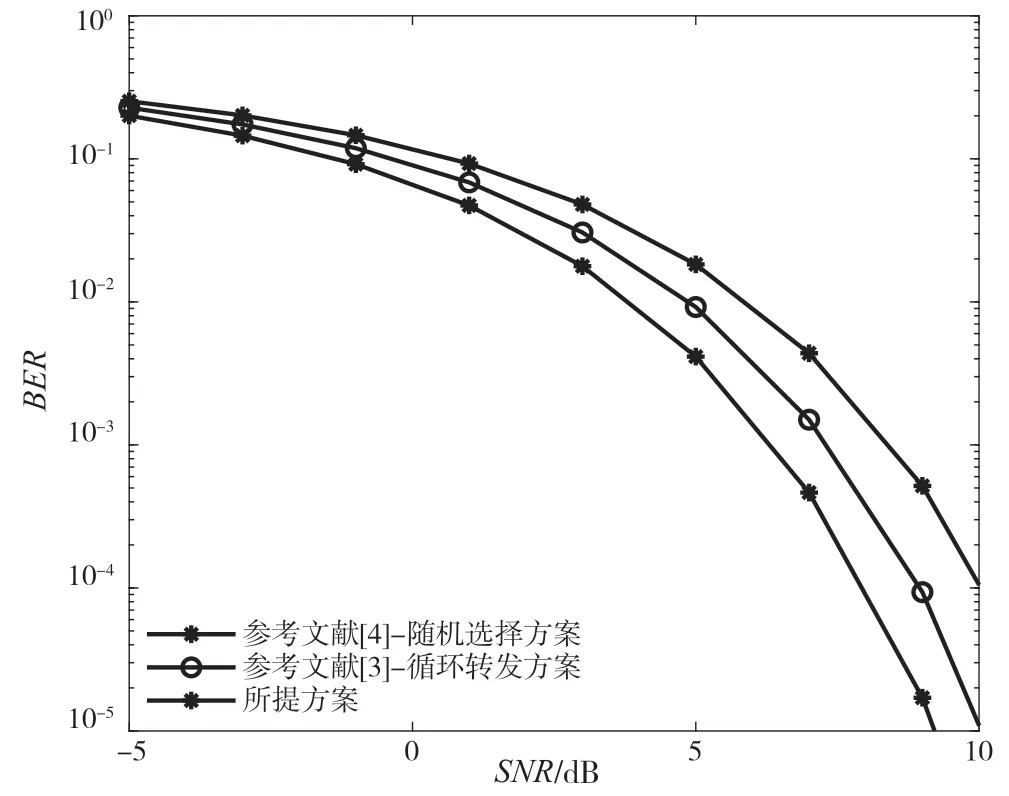
图4 中继选择方法对系统性能的影响

图5给出了在估计误差的方差为1/(3(P/N0))的情况下，系统中调制阶数与接收天线数目对系统误比特率的影响。分别令调制阶数M取2（BPSK）或4（QPSK），接收天线数目Nr为2或4，图中标记符号表示不同的调制阶数和接收天线数目的组合。

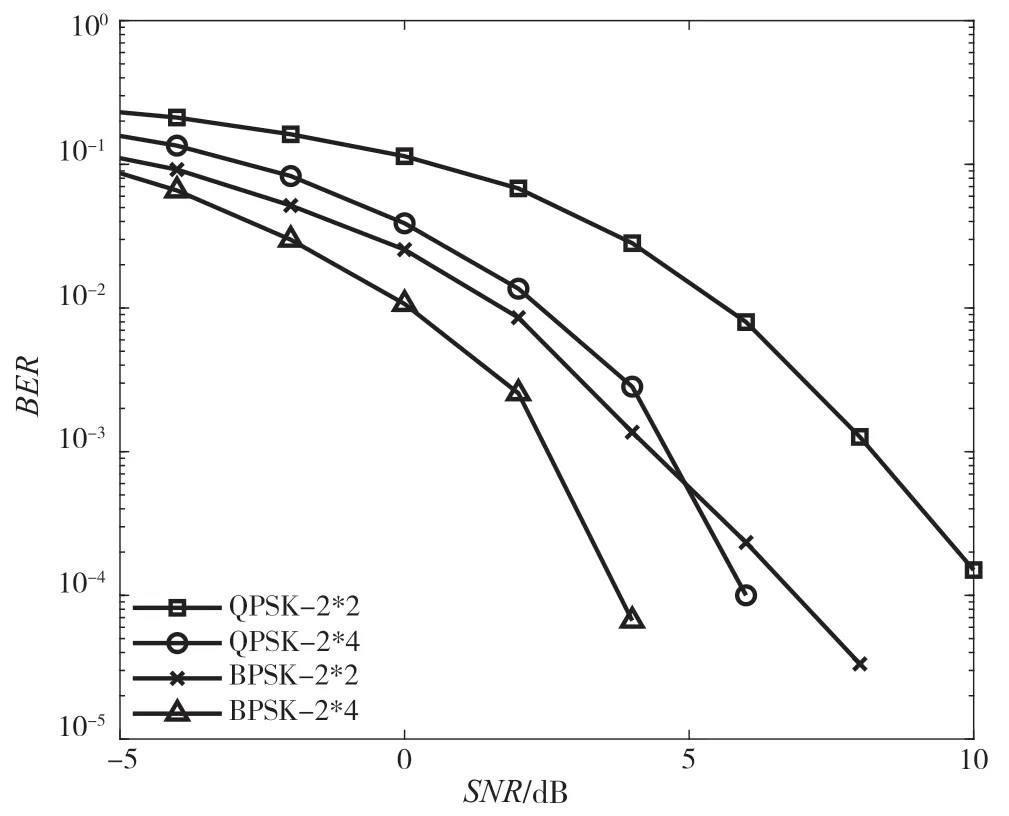
图5 调制阶数和接收天线数目对系统误比特率的影响

可以看出，当采用QPSK调制，且接收天线数目为2时，系统的误比特率最高，当采用BPSK调制，且接收天线数目为4根时，系统的误比特率最低，可以看出误比特率会随着系统调制阶数的减小或接收天线数目的增多而降低。这是因为当系统的接收天线数目固定时，调制阶数越高，星座图中相邻星座点的距离就越小，在解调时越容易产生错误，误比特率会增高；当系统的调制阶数固定时，接收天线的数目越多，在目的节点接收到的来自源节点所传输的信号的副本就越多，因此信号就会恢复得更准确，误比特率会更低。从图中还可以看出，较高信噪比时在不同的估计误差的方差下系统的误比特率曲线趋于平行，表明在接收天线数目不变的情况下，仅改变系统的估计误差的方差不会改变系统的分集增益。

4 结语

本文给出了应用LRS中继选择方法时不完全CSI下的AF-SM系统的误码性能分析。在协作通信与空间调制系统相结合的系统中，考虑不完全CSI的系统将会更接近真实情况。针对使用LRS中继选择方法的AF-SM系统，分析了存在信道估计误差时系统的误比特率性能，以及高信噪比下的渐近误比特率，并研究了两种不同的信道估计误差对系统性能的影响。本文所提出的应用LRS方法的AF-SM系统只给出了节点等功率分配的情况，为进一步提高传输的可靠性，降低系统的误比特率，未来将考虑对源节点和中继进行功率分配。