天电背景下低频弱信号混沌接收方法*

张 洋，芮国胜，毛忠阳，刘锡国，赵志勇

（海军航空大学，山东 烟台 264001）

0 引言

低频信号因其具有绕射能力可获得远距离传输的优势，且信号不易受电离层影响，在导航、标帜、低频授时、地震监测等领域获得了广泛应用，另外低频信号容易穿透海水和土壤，便于进行海洋和地质勘探研究。然而低频信号容易受到恶劣大气环境尤其是天电噪声的影响，低频信号到达接收端时呈现出信号弱、信噪比低的特点，从而导致传输不畅甚至中断。

传统的天电噪声处理方法是限幅、削波方法[1-3]，此方法在20世纪70年代被广泛采用，近年来缺少新理论和新技术的突破，消噪方案和结构都没有太大的更新和改变。该方法虽然可将天电噪声中的大部分脉冲成分消除掉，但同时也会使有用信号损失，此方式在天电噪声脉冲成分所占比例较小时，对通信系统的接收性能有一定程度的改善。但当噪声较强时，消噪效果较差且没有从根本上解决低频信号接收问题。

因此，本文着眼于探索新的天电噪声处理方法，将混沌接收机理应用到低频弱信号接收过程中，实现天电噪声背景下低频弱信号的接收。

1 天电噪声特性分析和建模

低频信号在地—大气波导中的传输比较稳定，传输距离远，且频段内主要噪声源为天电噪声。为了运用混沌机理实现低频弱信号接收，有必要先对大气噪声的统计特性进行研究。

1.1 天电噪声统计特性分析

低频频段的噪声主要是由天电瞬时放电引起的，表现为强脉冲噪声形式。其天电脉冲噪声形式主要由接收机附近的闪电电磁脉冲叠加而成，主要表现为脉冲能量强、持续时间短，且噪声能量主要集中在脉冲分量上。

工程实验表明，干扰低频信号的噪声是由背景噪声和脉冲噪声相加而得：

式中，n(t)是总的噪声，可看作是两个独立的随机过程之和；w(t)是背景噪声，一般认为是来自大范围的大气噪声叠加组成，总体表现形式趋于均值为零、方差为σ02的高斯随机过程；v(t)是脉冲部分，可以看成随机产生的大量窄脉冲之和，可用单位冲激函数来表示：

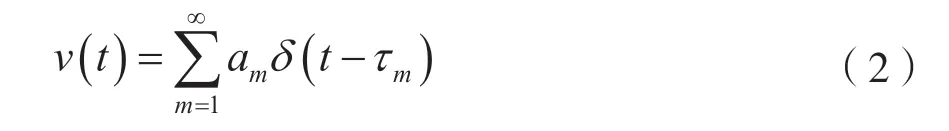
式中，am为随机脉冲的幅度，τm为随机脉冲延迟，且随机幅度am、τm与噪声n(t)相互独立。

脉冲噪声的特性就是由随机幅度和随机延迟决定的。此外，有两个特殊的参数常用于描述天电噪声的统计分布，即幅度概率分布和脉冲间隔的统计。

1.2 天电噪声模型的建立

研究基于混沌振子的低频弱信号接收问题，必须对接收机的前端噪声进行建模。为此需要一个合理描述天电噪声特性，并适合低频传输系统的仿真噪声模型。

噪声在达到接收机之后，首先通过的是接收机的前端滤波器，所以观察到的天电噪声实际上是接收机滤波器的通带上的窄带噪声。对于低频弱信号，接收机带宽相对于频带中心频率来说充分得小，一般来说是中心频率的10-2左右，使得接收到的天电噪声可被假设为一个窄带随机过程。在实际传输过程中，这个假设条件通常可以得到满足，并且远非高斯分布特性严格，因此噪声的建模问题可以被简化。

对天电噪声的测量数据表明，天电噪声在低幅度部分表现为高斯特性，在高幅度部分的包络表现为近似指数正态特性。由于高幅度对传输系统性能的影响更大，因此模型侧重于天电噪声的指数正态特性。用以下形式将天电噪声模拟为一个具有指数正态包络的窄带过程：

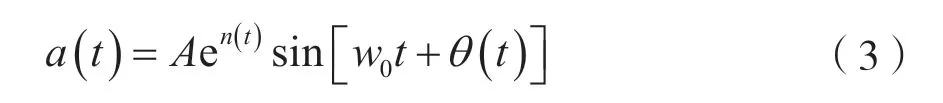
式中，n(t)是一个平稳高斯随机过程，其均值为0，方差为A是一个常数（由噪声功率估计确定）；θ(t)是随机相位过程，独立于高斯过程n(t)。对天电噪声瞬时频率分布的测量结果表明，θ(t)与窄带高斯噪声的频率分布相似，也就是说，即使天电噪声的包络分布与高斯噪声在大包络值时不同，但它们的相位和频率部分却十分类似。因此假设θ(t)具有类似窄带高斯过程的相位的特性，意味着在任何给定的时刻t0，相位θ(t0)为一个均匀分布于[0，2π]上的随机变量，并且独立于包络。

天电噪声的指数正态窄带噪声模型由式（4）给出。噪声的包络为：

考虑包络的平均电压和均方根（Root Mean Squre,RMS）电压，其平均电压为：

RMS电压为：

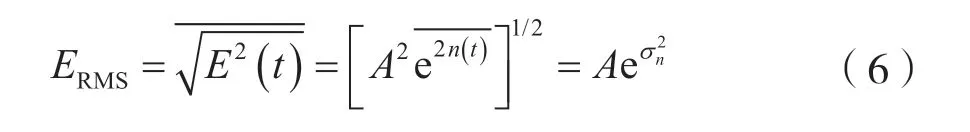
定义电压偏差Vd为：

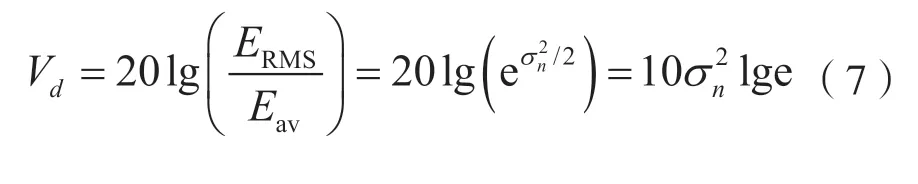
对Vd的认识给出了的值，Vd的值在国际无线电咨询委员会（Consultative Committee on International Radio，CCIR）报告中给出相应的定义。Vd用来确定天电噪声的包络en(t)中随机过程n(t)的方差它决定了天电噪声中的脉冲成分所占的比例。可以认为，不同的Vd值代表了不同天气情况下的天电噪声，Vd越大，则表示接收机所处位置的天气越恶劣，大气中的天电越剧烈。例如，Vd=2时可以认为是普通的天气环境，Vd=4.5时认为是稍差的天气环境，而Vd=7和Vd=10时则表示接收机已处于雷电交加的气候环境中。

基于前述指数正态包络过程，建立天电噪声模型的仿真流程图如图1所示。

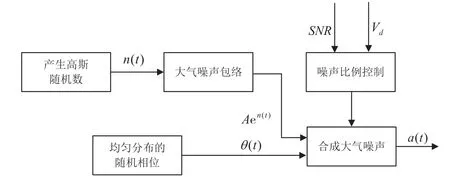
图1 天电噪声模型仿真流程图

2 天电噪声背景下的正弦弱信号混沌接收

理论与仿真实验均表明，混沌振子对任何均值为零的噪声，无论其是白噪声还是色噪声，都具有很好的抑制能力，零均值噪声的加入不会改变系统原有的运动状态，只是体现在相轨迹的粗糙程度上。

考虑由式（3）定义的天电噪声的均值：

随机过程n(t)和θ(t)相互独立，所以由式（8）得：

由于θ(t)在[-π,π]均匀分布，所以：

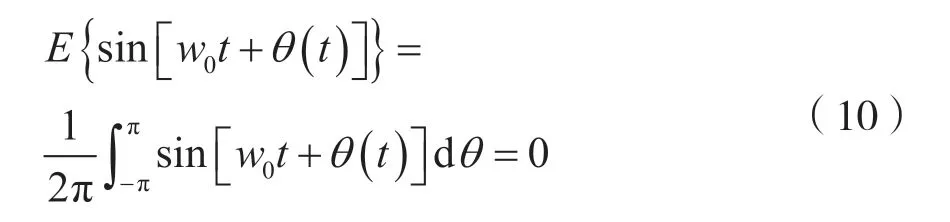
指数正态窄带噪声模型定义的天电噪声的均值为零。

由式（10）可知，天电噪声的均值恒为零，也就是说混沌振子对天电噪声同样具有一定的抑制作用。利用混沌振子接收被天电噪声污染的低频信号可以充分发挥混沌振子优良的抗噪声性能，为实现天电噪声背景下低频信号的可靠接收提供了理论基础。

对天电噪声背景下混沌接收系统的抗噪性能进行实验分析。前面的分析指出，电压偏差Vd可以用来确定天电噪声的包络en(t)中随机过程n(t)的方差，它决定了天电噪声中的脉冲成分所占的比例。分别设置Vd=2、4.5、7和10，按照图1所示的流程对天电噪声进行仿真，得到不同Vd值下产生的天电噪声包络如图2所示。仿真过程中，噪声幅度包络设为A=1，信号与天电噪声中的背景高斯白噪声的功率比为SNR=0 dB。

由仿真结果可以看出，在较小的Vd（Vd=2）时，噪声中的脉冲成分所占的比例较小，此时的噪声主要表现为高斯特性，如图2（a）所示；而随着Vd值的增大，噪声中的脉冲成分也会增加，瞬时脉冲的峰值也会随之增大。此时的脉冲成分集中了噪声的大部分能量，在脉冲持续时间内，噪声电平可能是信号的几十倍甚至上百倍，如图2（b）、图2（c）和图2（d）所示，此时有用信号被完全淹没，即使增加信号的功率也无法削弱噪声对系统接收和性能的影响。在利用混沌振子接收强天电噪声背景下的微弱低频信号[4-7]时，接收模型为：

图2 不同Vd 值下产生的天电噪声包络

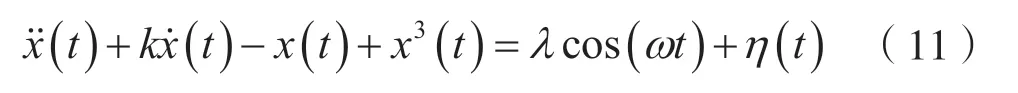
式中，acos(ωt)为待测信号，η(t)为随机噪声电压偏差。各参数设置如下：系统阻尼比k=0.5，初值设定为(x,x˙)=(0,0)。采用Euler-Maruyama算法对系统进行积分运算，仿真步长为h=0.01s，系统内置周期策动力频率为ω=1 rad/s，积分时间取为1 000 s。

调整系统的内置周期策动力强度，使系统处于临界状态，如图3所示。

图3 临界态时系统相图及x 的瞬时频率

Vd分别设置为2、4.5、7和10。待测信号强度为B=0.02 V，然后分别加入受到不同强度天电噪声污染的低频弱信号，天电噪声的强度主要由幅度包络值A决定，通过系统是否发生相变来实现对不同强度天电噪声背景下待测信号的接收[8-12]，研究不同环境中基于混沌接收算法的抗噪性能及工作信噪比门限，仿真所得结果如图4所示。

Vd较小时（Vd=2），噪声主要表现出高斯特性，调节A=0.31，被天电噪声污染的待测信号如图4（a）所示，待测低频弱信号完全淹没在噪声中，在混沌接收系统中加入含噪待测低频弱信号，系统迅速发生相变跃变到大尺度周期态，系统输出的相图如图4（b）所示，待测信号的信噪比为-30 dB。

图4 混沌接收振子的状态Vd=2

Vd较大时（Vd=4.5），噪声中的脉冲成分将继续增加，调节A=0.06，被天电噪声污染的待测信号如图5（a）所示，加入含噪待测低频信号，整个系统迅速发生相变跃变到大尺度周期态，系统输出的相图如图5（b）所示。此时系统实现的信号接收门限为-25 dB。

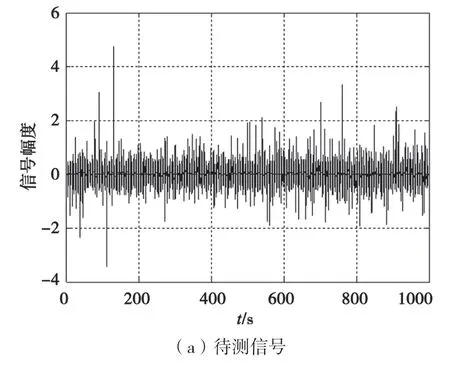
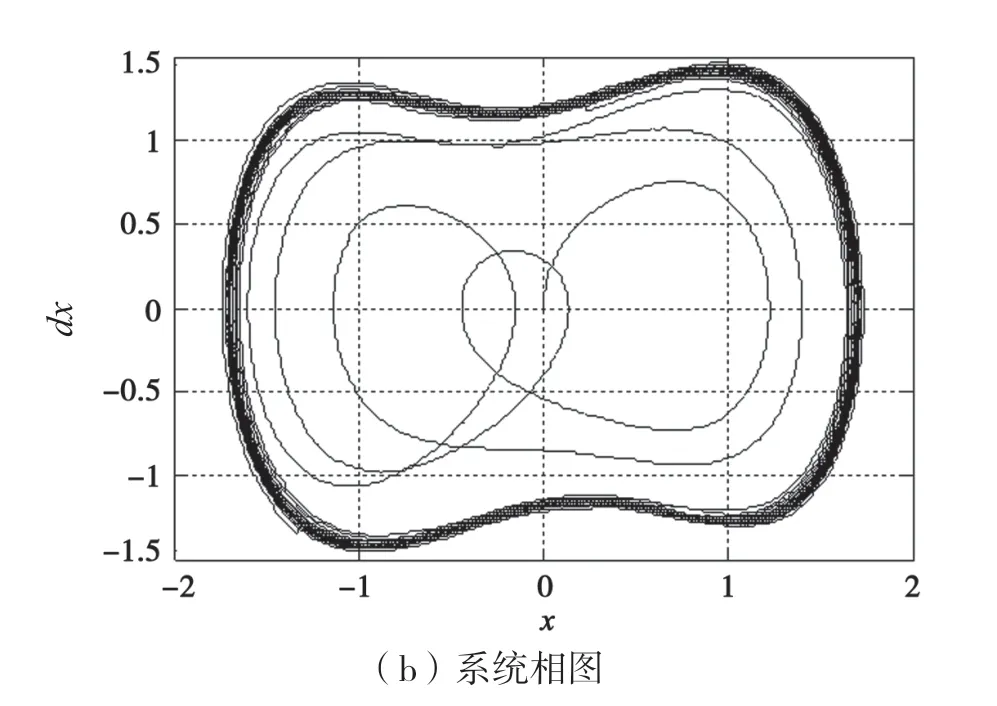
图5 混沌接收状态Vd=4.5

继续增大Vd值（Vd=7），此时的天气环境已经比较恶劣，噪声中的脉冲成分和能量进一步增加，调节至A=0.012时，被天电噪声污染的待测信号如图6（a）所示，加入含噪待测信号，系统迅速发生相变跃变到大尺度周期态，系统输出的相图如图6（b）所示。此时，系统实现的信号接收门限为-19 dB。

图6 混沌接收振子的状态Vd=7

Vd非常大（Vd=10）时，表示天气环境非常恶劣，噪声将以脉冲能量为主，调节至A=0.000 8时，被天电噪声污染的待测信号如图7（a）所示，加入含噪待测信号，系统迅速发生相变跃变到大尺度周期态，系统输出的相图如图7（b）所示。系统可实现的信号接收门限为-13 dB。此外，由仿真结果注意到当存在大幅度脉冲噪声时，相图轨迹出现了较大的毛刺，系统的轨迹不再平滑。

图7 混沌接收振子的状态Vd=10

仿真结果表明，本文提出的基于混沌振子的低频信号接收方法对天电噪声具有很强的免疫性，可以应用于天电噪声背景下的低频弱信号接收。本文算法对于任意零均值未知分布噪声均具有极强的抑制能力和较低的信噪比工作下限，这是目前其他现有的信号处理方法所无法比拟的。本文算法所具有的接收普适性，使它在微弱低频信号接收中具有很大潜力，是一种极具发展前景的接收方法。

3 结语

有效地在强天电噪声条件下增强弱信号接收能力是亟待解决的一个重要问题。为此本文给出了基于混沌振子的低频弱信号接收方法，并对天电噪声的统计特性进行了研究和建模分析，通过仿真分析了天电噪声环境下本文算法的接收性能。实验结果证实了文中算法在复杂天电噪声背景下的接收可靠性，对提高现有低频信号接收的性能具有一定的指导意义。