GPS 高程曲面拟合对变形监测精度的分析

巨金胜，刘青锋

自然资源部第三地形测量队，黑龙江 哈尔滨 150000

1 GPS 高程与正常高、正高的关系

正常高、正高和大地高的关系如图1 所示。其中，点P 为地表任意点；Hq为点P 至参考椭球面的高度，即大地高；H 为点P 至大地水准面的高度，即正高；Hr为点P 至似大地水准面的高度，即正常高。数学表达式如下：

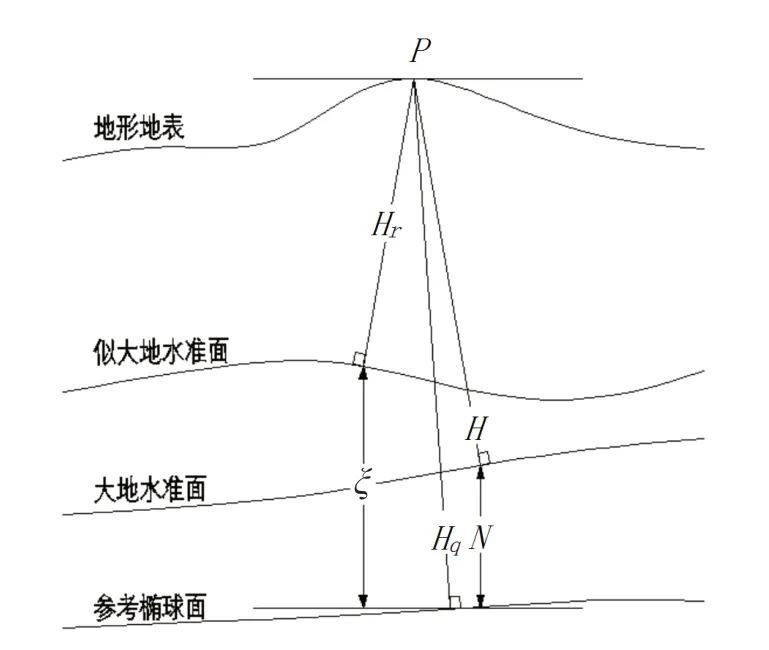
图1 正常高、正高和大地高的关系

通常，应用GPS 技术获取的高程都是基于WGS-84 参考椭球面的大地高Hq，而实际测量中主要采用的多是基于似大地水准面的正常高Hr。通过GPS 技术获取地面点高程数据时，各观测点的高程虽然进行了高程异常值ξ 的修正，但小范围的GPS 观测通常采用的是短基线模式，在解算过程中采用的高程异常值ξ 存在一定的随机误差。

2 GPS 高程拟合原理及技术手段

GPS 高程拟合主要是通过数学方法极大限度地降低大地高和正常高之间的差异值，进一步提高GPS 数据的应用性和准确度。目前主要的处理方法有曲面拟合法、解析内插法、等值线图法等。在构筑物沉降、平坦地面沉降、山体滑坡监测等不同变形监测中，可以依据实际情况选取合适的解决方案。文章主要介绍曲面拟合法，具体原理：首先，采用GPS 技术进行变形监测，同时使用二等水准测量模式联测变形监测点，同步获取变形监测点的GPS 高程与水准高程，并通过已知高程获取各联测变形监测点的高程异常值ξ。其次，采用曲面拟合法，对各监测点的高程异常值ξ进行拟合，搭建局部似大地水准面，进而使用数学方法获取各变形监测点的高程异常值ξ，并求取各点的拟合正常高。最后计算相应的形变量。

3 监测应用

3.1 实例分析

文章主要对GPS 高程曲面拟合法在大桥变形监测中的应用进行精度分析。该大桥长580m，属于筋混凝土公路大桥。在此次变形监测过程中共设置8 个监测点，每个点均设立混凝土观测墩，并埋设稳固、良好的强制对中基座，如图2所示。全程采用静态观测模式，分两个时段对各个监测点进行观测。为了消除或削弱GPS 接收机端相关误差，需要使每个监测点接收机的天线高度均大于1.5m；另外大桥周边有大面积水域，会产生多路径效应，因此需要使用设计良好带有扼流圈的天线。在GPS 静态观测完成后采用二等水准方式再次对各监测点进行变形监测，获取各监测点的水准高程。

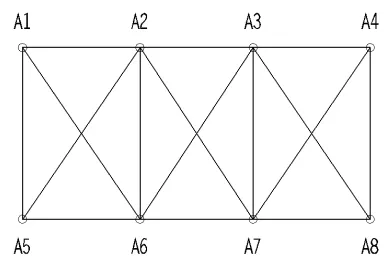
图2 大桥变形监测布点略图

3.2 成果

对两个时段的GPS 静态观测结果分别进行基线结算，获取相应的GPS 高程，并采用多项式曲面拟合法拟合平差后的GPS 高程得出拟合正常高。分别计算各变形监测点的GPS 曲面拟合形变量与二等水准形变量，并进行分析比较。

此次变形监测GPS 高程控制网的误差主要由三部分组成：

（1）GPS 静态观测过程中存在的误差，即GPS 高程测量误差X1；（2）求取高程异常值ξ 过程中存在的误差，即二等水准联测误差X2；（3）通过曲面拟合获取变形监测点拟合正常高过程中存在的误差，即高程拟合误差X3。故整个监测成果的误差X 与上述三类误差的关系如下：

前文已说明在进行静态观测时，已有效消除或削弱传播路径误差和接收机端误差，故X1主要为卫星端误差和相应的电离层效应误差，该误差为系统误差x1。同样，X2主要为二等水准测量的观测误差，在求取高程异常值ξ 后，该项观测误差可以视为系统误差x2。已知变形监测点A 已完成相关监测，两次变形监测成果拟合高程h1、h2：

由上可知，X1、X2都可以在求取形变量的过程中被消除，故影响最终形变量精度的因素只有X3，文章将针对此次大桥变形监测成果具体分析X3对变形监测整体精度的影响。

将两个时段观测所得出的GPS 正常高精度分析如表1所示。由表1 可知，1 ～8 号变形监测点GPS 静态观测结果良好，满足相关精度要求。将二等水准联测后经过平差得到的变形监测点水准高程作为已知值，通过基线解算获取GPS 正常高，并通过曲面拟合法获取拟合正常高，将其进行比对，得出相关数据分析如表2 所示。分析表2 可知，相比于GPS 正常高，拟合正常高的精度更加接近二等水准测量结果，而且拟合效果良好。现将已有8 个变形监测点的二等水准变形监测结果与GPS 曲面拟合变形监测成果进行分析比对，如表3 所示。

通过对上述成果数据的分析可知，采用曲面拟合法拟合GPS 高程后获取的拟合正常高可以达到二等水准测量的技术要求，而且精度较高，能够很好地满足了对大桥、高楼等各类构筑物进行变形监测的迫切需求。

4 结束语

GPS 技术在此类变形监测项目中的应用使变形监测的时空采样率飞速上升，为构筑物等的形变分析提供了丰富的数据信息。另外，采用GPS 测量可实现全天候作业，具有观测速度快、效率高、成本低等优点，可以广泛应用于高层建筑、特大桥梁、机场跑道等变形监测中。同时，随着智慧城市的大力推进，GPS 技术可与大数据有效集成，实现区块链模式的信息共享，为城市应急防灾提供坚实保障。

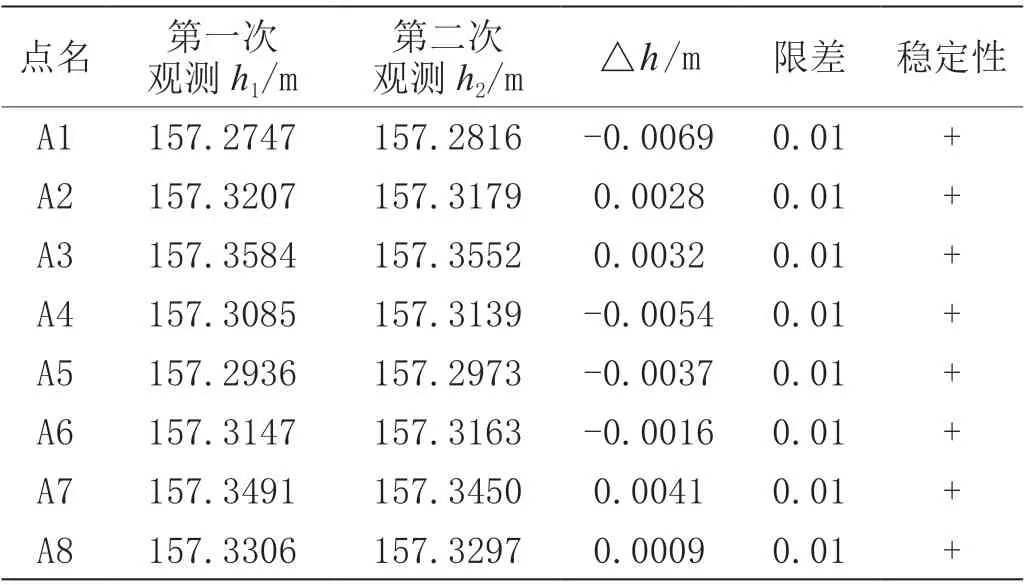
表1 两个时段下各GPS 变形监测点的稳定性分析

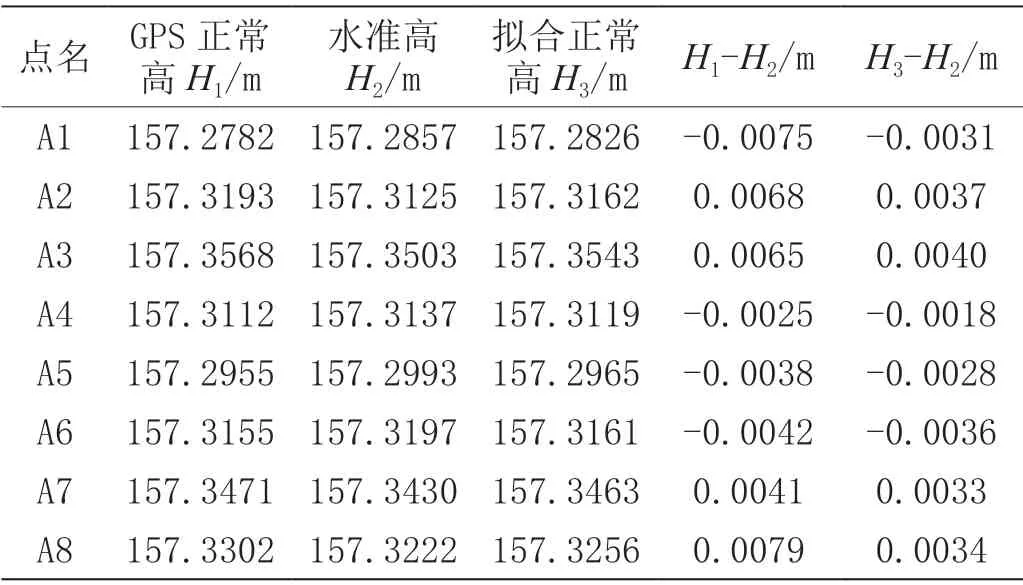
表2 各变形监测点多种高程分析比较

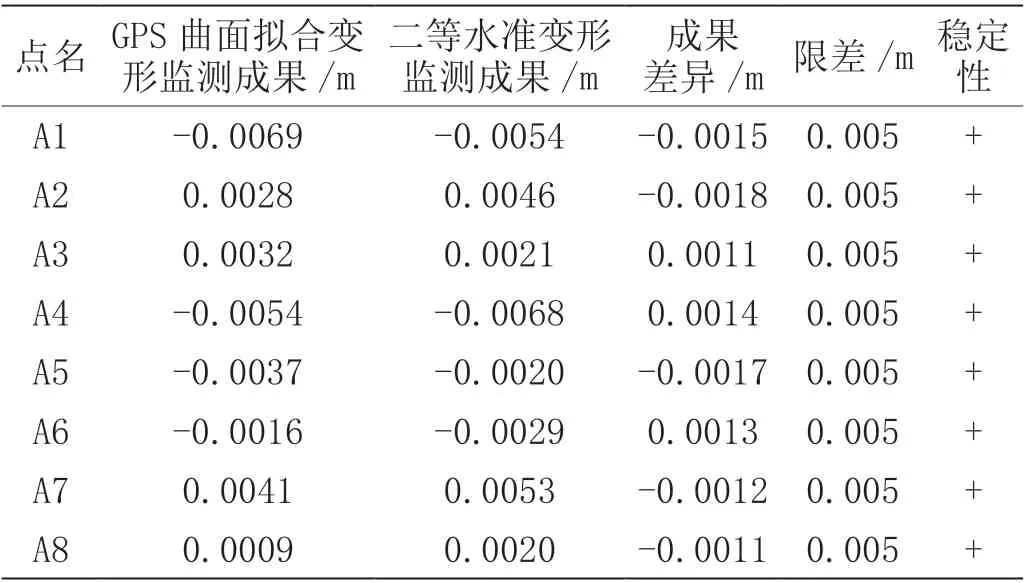
表3 不同模式下变形监测结果分析