初始位移作用下车身振动系统的能量消耗

周长峰，张家豪，鲁大坤，刘立邦，娄光浩

山东交通学院 汽车工程学院，山东 济南 250357

0 引言

在进行汽车振动、模态参数辨识等试验研究时，通常要获取车身的振动固有频率和阻尼比等参数，多采用偏频试验和正弦扫频的方法，由于车轮的跳动与车身的跳动相互耦合，为了消除车轮跳动的影响，需要固定轮毂，将整个车身看作是一个垂向振动的单自由度系统。文献[1-9]论述了振动系统受力平衡方程、频率响应特性、路面输入激励下的响应等方面的内容。如文献[2]运用广义虚功原理建立汽车振动微分方程组，建立考虑路面不平整度因素的车辆振动数值模型，用以研究车辆的振动响应情况与车辆行驶速度和公路路面状况之间的关系，得出以下结论：相同车速情况下，随着路面状况变差，车体振动强度呈现几何级数增大的趋势；相同路面等级情况下，车体振动强度随车速增大而增加，但存在一个车速增大而车体振动强度不再增大的平缓区间。文献[10]分析了阻尼振动系统的欠阻尼、过阻尼、临界阻尼3种状态，并叙述了受迫振动系统中能量损耗和能量补充问题。文献[11-14]推导了有阻尼单自由度系统的强迫振动通解，分析了振幅和频率比、阻尼比的关系。文献[15-20]分别建立了车辆悬架振动数学模型，并考虑对减振器消耗的能量进行回收。文献[21-25]建立了主动悬架的汽车振动微分方程，并对它们的响应进行了分析，结果表明安装主动悬架的汽车乘坐舒适性有很大提高。

当前的研究以主动悬架和振动能量回收为热点，但上述研究中未见初始位移作用下车身振动系统能量消耗的详细阐述。本文推导初始位移作用下车身垂向振动系统减振器在一个周期内能量消耗的计算公式，以及此工况下振动系统停止振动需要满足的周期数量，以便对车身振动系统进行模态参数辨识时，可以有针对性地改变车身振动系统的相关参数，使之产生多个周期振荡，从而更精准地识别车身振动系统的模态参数。

1 车身振动系统初始位移下的响应

刚性固定车辆的行驶系统，只对车身施加一个初始垂向位移，所引起的系统振动与单自由度系统振动类似。单自由度车身振动系统主要由车身、弹簧、减振器组成，其单自由度模型如图1所示。图1中：m为车身质量；k为弹簧刚度系数；c为减振器阻尼系数；O为车身振动系统静平衡位置；-x0为初始位移；F(t)为简谐振动的外激励力，F(t)=F0sin(ωt),其中F0为力幅，ω为激励圆频率，t为系统的振动时间。

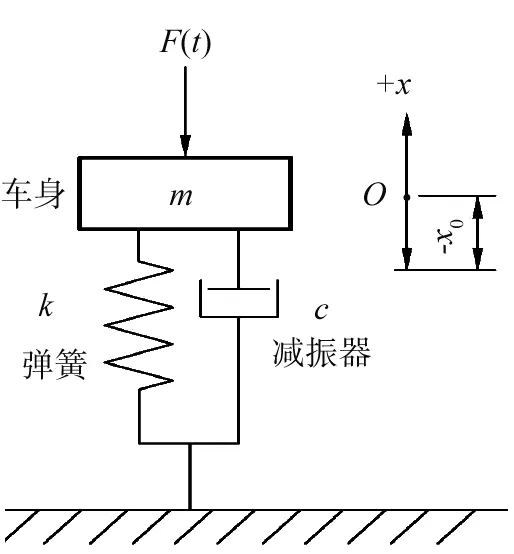
图1 单自由度车身振动系统模型

由牛顿力学定律可得单自由度振动系统在简谐激振力作用下的振动微分方程

(1)

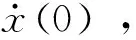
(2)

令k/m=ωn2，ωn为无阻尼固有频率；令c/m=2ξωn，ξ为振动系统的阻尼比，0<ξ<1。将式(2)进行因式分解和拉普拉斯反变换，可得在初始状态下系统的位移响应

(3)

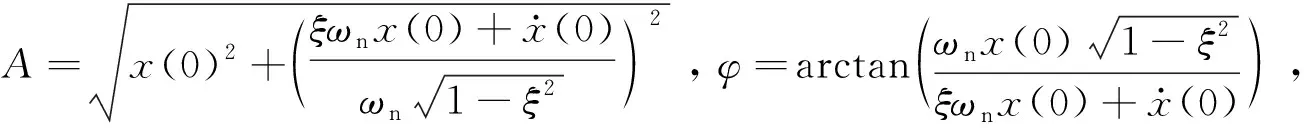
(4)

单自由度车身振动系统的位移曲线如图2所示，图2中车身位移响应曲线的相邻两个峰值(振幅)A1、A3之比称为减幅系数η，由图2及式(4)可以看出：

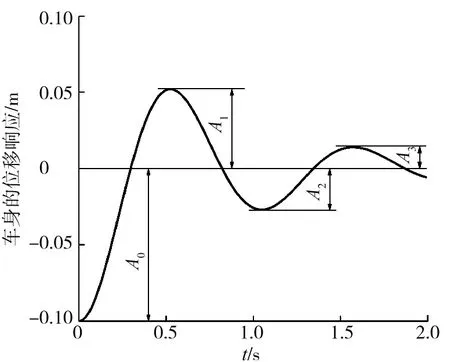
图2 单自由度车身振动系统的位移

(5)

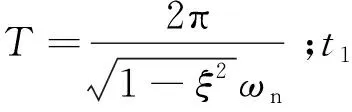
2 初始位移响应中各部件的功

2.1 弹簧做功

如图1所示，当m在恒定载荷F作用下向下运动x0并停止在该位置，运动过程中忽略阻尼器的影响，载荷F与弹簧所做的功分别为

(6)

(7)

由式(6)(7)可以看出：载荷F的功全部转化为弹簧的弹性势能。m在第一个振动周期内车身的运动状态以及弹簧做的功如表1所示。

表1 一个周期内车身的运动状态及弹簧做的功

2.2 减振器做功

减振器在一个周期内消耗的能量

(8)

由式(4)可知各时刻m的运动速度

(9)

将式(9)代入式(8)，计算得到第一个周期内减振器消耗的能量

(10)

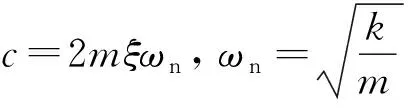
(11)

由式(11)可以看出：在仅由车身初始位移引起的振动中，车身振动系统减振器消耗的能量只与阻尼比有关，与车身振动系统的固有频率无关。

假设减振器每个周期消耗的能量为Wci，则n个振动周期内减振器消耗的能量

(12)

当车身振动系统的输入功被消耗掉Ws(Ws为百分数)时，振动基本结束，因此车身振动系统停止振动需要满足的条件为：

(13)

由式(12)(13)可计算经过n个周期振动基本结束。n越大，则振荡周期数越多，越便于在模态参数辨识时对车身振动系统进行数据采集。

3 算例

计算参数选取为：m=400 kg，k=15 kN /m，c=1 kN·s/m，x0=0.1 m,Ws=98%，由前述可求得ωn、ξ、A、η、Wk等参数。1～4个振动周期每个周期减振器消耗的能量分别为69.520、5.080、0.370、0.027 J，减振器消耗的能量占总输入功的百分比分别为92.700%、99.500%、99.960%和99.997%。由此可知：随着时间增加，各个周期内减振器消耗的能量逐渐减小，消耗的能量与η2成反比。相邻两周期前者与后者所消耗的能量的比值为η2。根据式(13)计算得到n≥1.493，车身振动系统在1.5T内其振动能量衰减了总输入功的98%。

c不同时减振器所消耗的能量如图3所示。由图3可以看出：c较大时，减振器消耗的能量在较短的时间内达到了75 J，c越大，达到75 J的时间越短；当c较小时，振动系统持续振动的时间增加。相同时间内，c越大，减振器消耗的车身振动系统的能量越多。

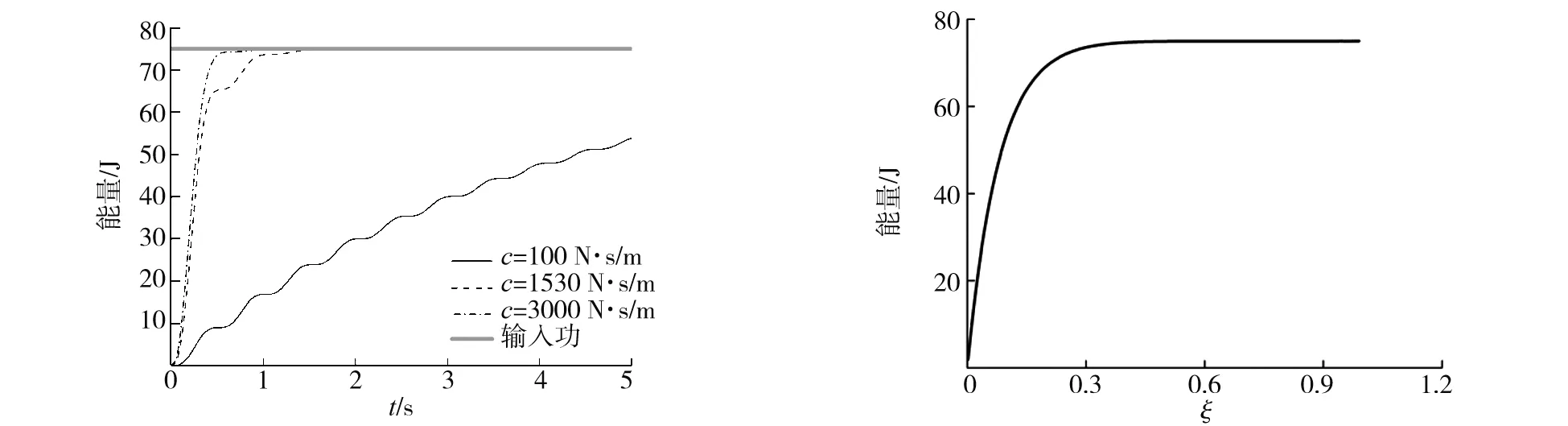
图3 阻尼系数不同时减振器所消耗的能量 图4 减振器消耗的能量随阻尼比的变化关系

第一个周期内减振器消耗的能量随ξ的变化关系如图4所示。由图4可知：随着ξ的增大，振动系统第一个振动周期内消耗的能量逐渐增大，但ξ增大到0.3时，减振器第一个周期消耗的能量达到了73.56 J，占此状态下总输入功的98%。

当k、c不变，m改变时，车身振动系统的加速度响应波形如图5所示。当m、c不变，k改变时，车身振动系统的加速度响应波形如图6所示。

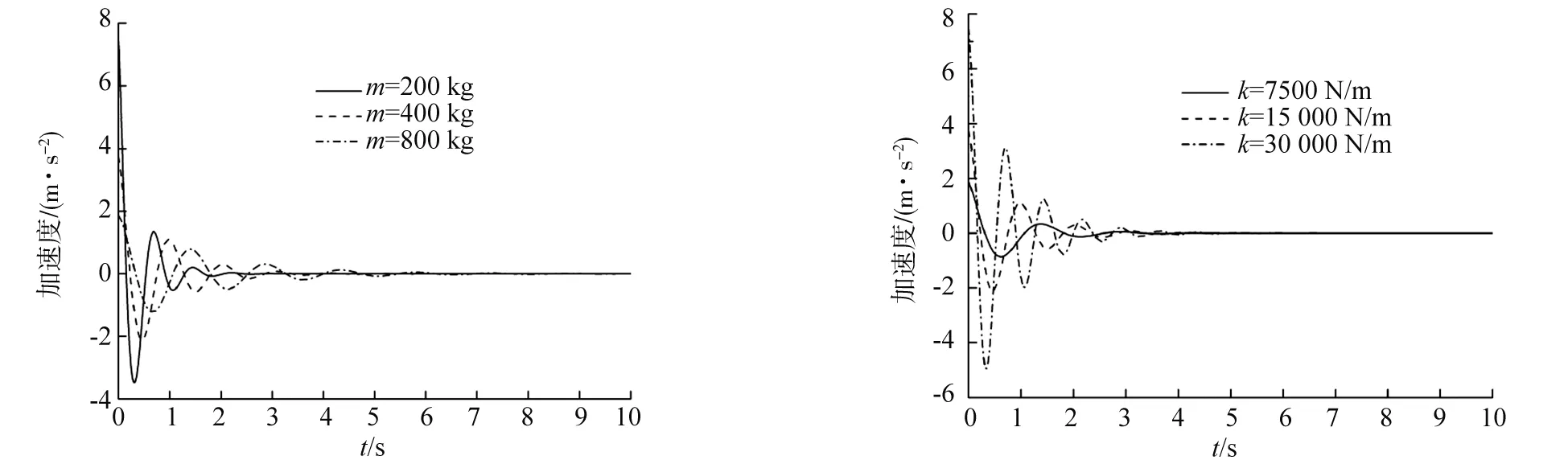
图5 质量改变时车身振动系统的加速度响应 图6 刚度改变时车身振动系统的加速度响应

由图5、6可以看出：当k、c不变时，增加m，车身振动响应的周期变长、达到振动基本结束所需的振荡次数增加；当m、c不变时，k越小，振动周期越长，振动加速度幅值越小，k越大，振动周期变短，达到振动基本结束所需的振荡次数增加。因此在试验时，为减小每个周期减振器对车身振动系统能量的消耗，可以通过增加车身质量或换装大刚度系数的弹簧，再测量车身垂向振动的有阻尼振动响应，并通过多次改变结构的质量和刚度，得到车身振动系统的模态参数。

4 结论

1)在一个振动周期内，振动系统减振器消耗的能量随着阻尼比的增大而增大，当阻尼比增大到0.3时，减振器第一个周期消耗的能量达到总输入功的98%。减振器各个周期内消耗的能量逐渐减小，其消耗的能量与减幅系数的平方成正比。

2)进行车辆振动试验时，刚性固定车辆的行驶系统，只对车身施加一个初始垂向位移时，系统的振动与单自由度系统振动类似。要使车身振动响应的振荡次数增加，则需要减小每个周期减振器对车身振动系统能量的消耗，当刚度和阻尼系数不变时，需要增加车身的质量，当质量和阻尼系数不变时，则要增大弹簧的刚度。试验时，通过多次改变上述物理参数，即能确定车身振动系统的模态参数。