混合梁桥钢混结合段合理布置位置的优化
黄国红,官彩依,卓为顶
1.南京市公共工程建设中心,南京 210019;2.东南大学 土木工程学院, 南京 211189;3.南京工程学院 建筑工程学院, 南京 211167
0 引言
三跨连续梁应用广泛,其边跨与中跨长度比例与结构受力的均衡性及合理性密切相关。受地形和两岸接线等因素限制,常采用超短边跨的三跨连续梁布置方案。对于超小边中跨比的桥梁,为了避免边支座上出现的上翘拉力,常采用2种解决方案:1)边跨配重,如加拿大的Grand-mere桥[1],中跨和边跨分别长181.4 、39.6 m,边中跨比为0.22;2)主跨中段采用钢箱梁,形成钢和混凝土纵向组合的混合梁体系[2]。
目前国内外对于超小边中跨比桥梁的合理边中跨比、钢混结合段合理位置的研究较少。混合梁常应用于大跨度的斜拉桥和悬索桥中,部分学者研究了这类桥梁结合段的合理位置。刘高等[3]结合湖北鄂东长江公路大桥,提出主梁弯曲应变能和支墩反力分布是确定混合梁斜拉桥钢混结合部合理位置的两个重要因素,还应兼顾施工、经济等因素。徐恭义[4]结合广东汕头海湾大桥混合型斜拉桥方案的技术设计,提出结合段位置必须考虑内力小、变形小、锚跨长度合适、施工方便等原则。基于混凝土施工和质量控制便利的考虑,湛江海湾大桥(混合梁斜拉桥)的结合段设置在边跨辅助墩墩顶处[5-7]。
对于混合连续梁桥,张鹏等[8]提出结合段受力的合理位置应是混合梁内力和变形较小处,综合考虑受力、造价和施工3方面因素,采用层次分析优选法进行系统分析,并给出定性评价和定量评价相结合的关键要素评价法。黄丽[9]分析了不同钢梁长度下主梁跨中截面弯矩等参数随接头位置变化的规律,建立以接头处截面弯矩及剪力最小为优化目标的多目标优化模型,确定在约束条件下的合理接头位置。张少勇等[10]基于相同长度的钢箱梁段自质量约等于等效混凝土梁自质量的30%,比选瓯越大桥中跨的钢梁段合理长度。苏庆田等[11]提出了混凝土-钢混组合梁的新型混合梁桥构造设想,认为边跨长度和中跨组合梁长度相互影响,并以桥梁结构在运营过程中边支点不出现负反力作为限制条件,推导了最小边中跨比和中跨组合梁长度占比之间的关系。陈军等[12]认为选择结合段合理位置,应考虑混合连续梁桥中结合段局部应力分布规律及传力机理。
本文以南京机场二通道跨秦淮新河三跨变截面混合梁桥为研究背景,分析并推导超小边中跨比连续混合梁桥跨径布置及结合段合理位置的设计原则和设计理论,以期为同类设计提供参考。
1 工程背景
机场二通道跨秦淮新河桥是预应力连续箱梁桥,纵向采用钢-混组合结构,桥跨组合为200(35+130+35)m,如图1所示。桥梁为双幅布置,单幅桥面横截面布置为20(0.5+3.0+4.0+0.5+11.5+0.5) m,即人行栏杆+人行道+非机动车道防撞护栏+车行道+防撞护栏。
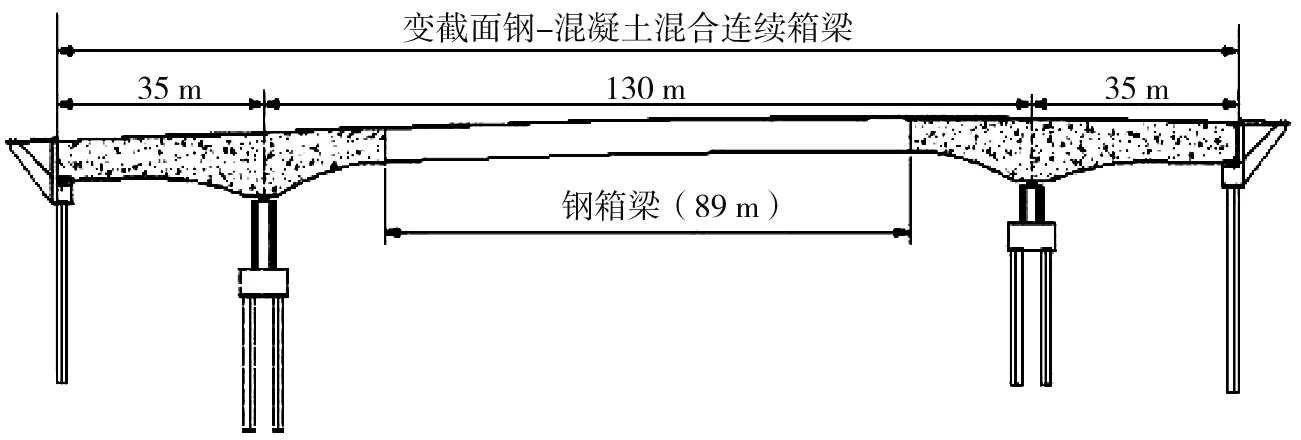
图1 秦淮新河桥桥型布置
主梁的混凝土梁段采用混凝土C55,钢箱梁段采用Q345D,普通钢筋采用HRB400,箍筋采用HPB300,纵横向预应力筋采用抗拉强度为1860 MPa、直径为15.2 mm的低松弛钢绞线,竖向预应力筋采用屈服强度为785 MPa、直径为32 mm的高强精轧螺纹粗钢筋。
受地形限制,秦淮新河桥的边中跨比为0.269(35/130),远小于常见的连续梁桥0.6~0.8。因此,中跨部分采用钢箱梁代替混凝土梁以减小中跨自重,增加边支座支反力。
2 混合连续梁桥跨径布置及结合段合理位置
2.1 基于中墩处截面弯矩等效的原则
基于弯矩等效的原则[13-15]确定混合梁中跨钢梁长度比值和边中跨比之间关系,任意设计参数确定的全混凝土梁以中墩截面弯矩等效为指标,边跨或中跨长度相同时,改变混合梁结合段位置,计算满足中墩处梁截面弯矩相同的边跨比。
2.1.1 混合连续梁桥中墩弯矩
三跨混合连续梁桥如图2所示,边跨长L1,中跨长L2,钢梁长度Ls,混凝土梁长度Lc。钢箱梁的自重荷载集度qs,混凝土梁的自重荷载集度qc,混凝土箱梁的抗弯刚度为EcIc,钢箱梁的抗弯刚度为EsIs。根据对称性,计算简图取半结构,如图3所示。

图2 三跨混合连续梁桥示意图

a) 连续梁桥半结构示意图 b) 结构力学示意图图3 三跨混合连续梁桥计算示意图
根据结构力学位移法[16],此结构的位移法基本方程为:
(1)
式中:Z1为中支座处梁的单位转角,Z2为钢混结合处梁的单位转角,Z3为钢混结合处梁的单位竖向线位移,rni为Zi发生单位位移在第n个位置产生的约束反力矩,Rnp为外荷载作用下在第n个位置产生的约束反力矩。
根据中支点截面和钢混截面的平衡关系,可得rni,代入式(1)则有:
(2)
式中:i1、i2、i3分别为全混凝土梁段、中跨混凝土梁段、中跨半钢梁段的线刚度,i1=EcIc/Lc,i2=EcIc/La,i3=EcIc/Lb;Lc、La、Lb分别为混凝土梁段、中跨混凝土梁段、半中跨钢梁段长度。
整理可得
(3)
式中:Ci1、Ci2、Ci3、Ci4为线刚度比例系数,Ci1=(2i2+i3)/(3i1i2+3i1i3+i2i3),Ci2=(i2+i3)/(3i1i2+3i1i3+i2i3),Ci3=(3i2+i3)/(3i1i2+3i1i3+i2i3),Ci4=i2/(3i1i2+3i1i3+i2i3)。
计算得三跨混合连续梁桥中墩弯矩
。
(4)
2.1.2 混凝土连续梁桥中墩弯矩
三跨等截面全混凝土连续梁桥如图4所示,边跨长L1c,中跨跨长L2c,计算简图如图5所示,只设支座处梁截面的转角作为超静定的冗余约束,ω1为中墩支座处节点角位移。

图4 三跨混凝土连续梁桥示意图

a)半结构示意图 b) 结构力学示意图图5 三跨混凝土连续梁桥计算示意图
该桥梁在中墩截面处的弯矩方程为:
r11ω1+R1=0,
(5)

由式(5)得
因此,三跨混凝土连续梁桥中墩截面处弯矩
定义全混凝土梁的边中跨比λc=L1c/L2c,则弯矩简化后的中墩截面弯矩
(6)
2.1.3 边中跨比与钢梁长度占比的关系
在保持边跨长度相等的情况下,使上述2种类型桥梁的中墩截面的弯矩相等,即Mc=Ms,可以得
(7)
简化可得边中跨比ξ和中跨钢梁长度占比λ之间的关系式
A(ξ)λ3+B(ξ)λ2+C=0,
(8)
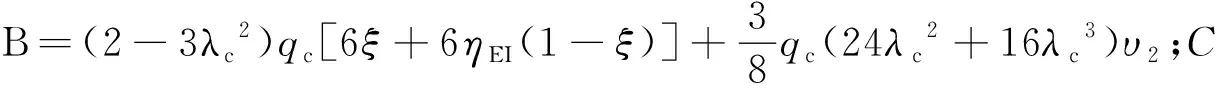
即对具有相同边跨长度L1c=Lc的三跨混合梁和全混凝土梁,在混凝土梁设计参数确定的条件下,总能找到边中跨比为ξ和中跨钢梁长度占比为λ的混合梁,使结构在中墩处的截面弯矩与之相等。
2.2 基于边支座支反力控制的原则
2.2.1 边支座支反力计算
边支座支反力计算主要考虑混凝土梁浇筑至最大悬臂长度阶段、中跨钢梁合龙阶段、桥面铺装阶段和运营阶段4个施工阶段的支反力及其叠加。
1)混凝土梁浇筑至最大悬臂长度阶段
由平衡关系可以得到
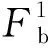
此时边支座支反力产生的力矩
2)中跨钢梁合龙阶段
中跨钢梁合龙时,结构的计算简图如图6所示。

图6 中跨钢梁合龙阶段计算示意图
根据结构力学位移法,可以得到此施工阶段的典型方程为:

根据平衡关系可得

3)桥面铺装阶段
桥面铺装完成后,结构的计算简图如图7所示。

图7 桥面铺装阶段计算示意图
根据式(1),可以得到:

4)运营阶段
运营阶段活载最不利布载如图8所示。

图8 运营阶段计算示意图
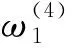
5)内力叠加
悬臂浇筑施工时,连续梁成桥后的总恒载内力是各个阶段不同体系内力叠加的结果。在正常运营阶段,三跨连续混合梁的边支座反力

2.2.2 边中跨比与钢梁长度占比的关系
在施工及运营过程中,将结构边支座始终受压作为控制条件,考虑边支座的压力储备Pr,研究混合梁桥中跨钢梁长度占比λ和边中跨比ξ的关系,应满足
整理后可得
3 算例
为简化计算过程,将秦淮新河桥混凝土主梁的变截面等效为等截面计算。秦淮新河桥钢箱梁的弹性模量为206 GPa,集度为qs=102.01 kN/m,抗弯惯性矩Is=3.551 m4;混凝土箱梁的弹性模量为35.5 GPa,自重载荷集度取为qc=741.00 kN/m,抗弯惯性矩Ic=48.527 m4,ηEI=0.425。
3.1 基于中墩弯矩等效原则
确定边跨长度为35 m,代入式(8),取混合梁中跨钢梁λ分别为30%、40%、50%、60%、70%和80%,计算满足中墩处截面弯矩等效的混合梁的跨径组合,主要参数及跨径组合见表1。

表1 中跨钢梁占比与边中跨比的关系
秦淮新河桥的ξ约为0.27,中跨钢梁λ约为0.69,符合弯矩等效原则。
3.2 基于边支座支反力控制原则
1)边支座不出现负反力
取中跨长130 m,当边支座无压力储备Pr时,针对不同的钢梁λ,根据式(7)(8),可得此时的钢梁与混凝土梁段长度、边跨长度等,如表2所示。

表2 边支座支反力为0时钢梁λ与ξ的关系
2)边支座保留Pr
取中跨长130 m,当边支座保留一定的Pr时,取Pr与边跨长度正相关,关系为Pr=0.2qcL1。根据式(7)(8)可得此时的钢梁长度、混凝土梁段长度、边跨长度等,如表3所示。

表3 边支座保留压力储备时钢梁λ与ξ的关系
3)ξ及钢梁长度可行域
根据计算结果,当确定中跨长度时,可以得到边支座支反力为零与保留一定压力储备时的λ与钢梁ξ之间的关系,因此可以得到合理的边中跨比与钢梁长度的取值范围,如图9所示阴影部分。
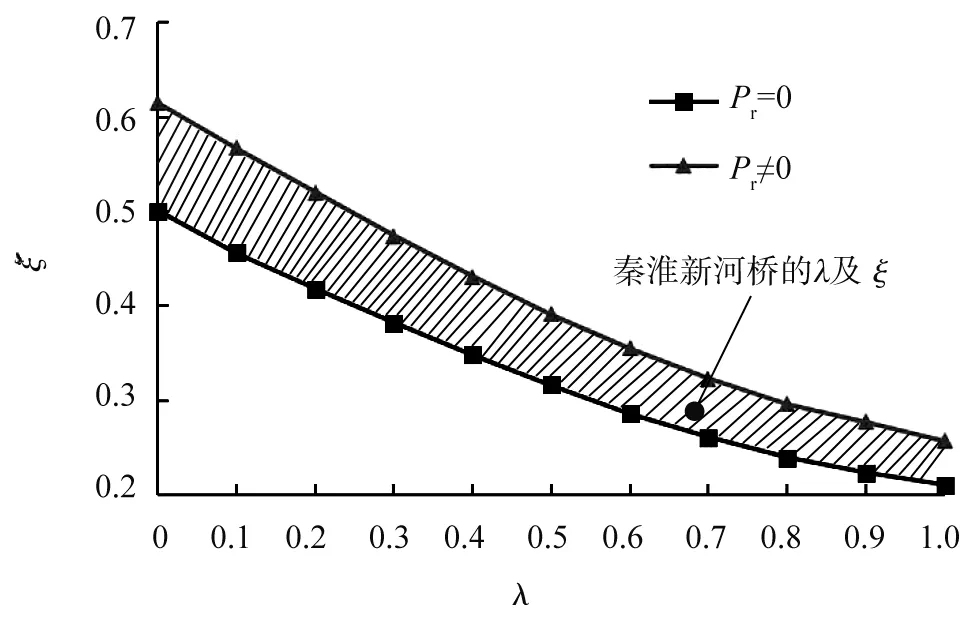
图9 边中跨比λ与钢梁长度占比ξ可行域
秦淮新河桥的ξ约为0.27,中跨钢梁λ约为0.69,λ与ξ处于可行域内,满足支反力控制原则,说明该桥梁结构的跨径和构造布置合理。
4 结语
针对中跨采用部分钢箱梁,形成钢和混凝土纵向组合的超小边中跨比三跨混合连续梁桥,本文以南京机场二通道跨秦淮新河桥为背景,基于中墩截面弯矩等效和边支座支反力控制两个原则,研究该类型桥梁跨径布置及结合段合理位置(即边中跨比与中跨钢梁长度占比)之间的关系。
1)建立计算模型,推导三跨混凝土梁和混合梁在中墩处的弯矩表达式,基于中墩弯矩等效原则,可得边跨长度相等时,混合梁的中跨钢梁长度占比和边中跨比的取值关系。
2)提出边支座支反力控制的原则。在施工及运营过程中,基于结构边支座不出现负反力准则,推导了三跨混合梁的内力表达式,考虑边支座处的压力储备,得到了边中跨比和中跨钢梁长度占比之间的关系。
3)边跨或者中跨长度确定时,根据中墩弯矩等效和边支座支反力控制原则,得到合理的边中跨比与钢梁长度占比。南京机场二通道跨秦淮新河桥的边中跨比约为0.27,钢梁长度占比约为0.69,处于合理范围内。

