求解奇异非线性方程组的改进的Levenberg-Marquardt方法*
覃雪冰,陆 莎,胡红红
(南宁师范大学 数学与统计学院,广西 南宁 530100)
1 引言
本文考虑非线性方程组
F(x)=0,
(1.1)
其中,函数F(x):Rn→Rn连续可微,并假设(1.1)的解集X*非空.文中,符号‖·‖表示矩阵或向量的2-范数.
牛顿法是求解非线性方程组的一类重要迭代方法,而Gauss-Newton方法是求解非线性方程组的一类基本方法.Gauss-Newton方法的迭代步为
其中Jk=F′(xk)是F在xk处的雅可比矩阵.在F(x)的雅可比矩阵在解值点非奇异且Lipschitz连续等条件下,牛顿法具有二阶收敛速度.为了克服牛顿法在雅可比矩阵奇异或接近奇异时无法求解的缺陷,不少学者对算法进行了改进.比如Levenberg[1]和Marquardt[2]提出了Levenberg-Marquardt(LM)方法.LM方法的主要迭代步为
(1.2)
其中Fk=F(xk),λk是一个非负参数.易见,dk1是凸函数
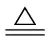
(1.3)
的极小值点.另一方面,如果记
则dk1也是信赖域子问题
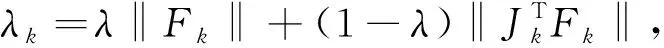
(1.4)

该LM参数是对(1.4)的进一步推广.
另一方面,为节约雅可比矩阵的计算量,Fan[9]提出一种改进的LM方法,该方法在每次迭代中除了计算一个LM步dk1,还计算一个近似LM步
(1.5)
类似于dk1,dk2可视为凸函数
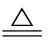
的极小值点.若令
则dk2也可以看成是信赖域问题
的解.关于含有一个近似步LM方法的推广可见文献[10]和[11],二者均在一般LM参数下对带一个LM步和一个近似LM步的方法进行改进,得到三阶收敛速度.在上述文献的基础上本文给出推广的LM参数,从而得到一个改进的算法,该算法在每次迭代中不仅计算一个LM步,而且计算一个近似LM步用以减少对应的雅可比矩阵的计算量,同时利用信赖域的思想确定是否接受试探步和更新LM参数的规则。最后讨论算法的全局收敛性和收敛速度.
2 改进的Levenberg-Marquardt方法
φ(x)=‖F(x)‖2
为其价值函数.设在第k次迭代中,φ(x)的实际下降量为
Aredk=‖Fk‖2-‖F(xk+dk1+dk2)‖2,
(2.1)
定义预测下降量
Predk=‖Fk‖2-‖Fk+Jkdk1‖2+‖F(yk)‖2-‖F(yk)+Jkdk2‖2
(2.2)
以及实际下降量与预测下降量的比值
(2.3)
类似于信赖域方法,利用rk来决定是否接受试探步以及更新LM参数规则.
以下给出改进的带近似步LM算法.
算法求解非线性奇异方程组的改进Levenberg-Marquardt方法(MLMPM)
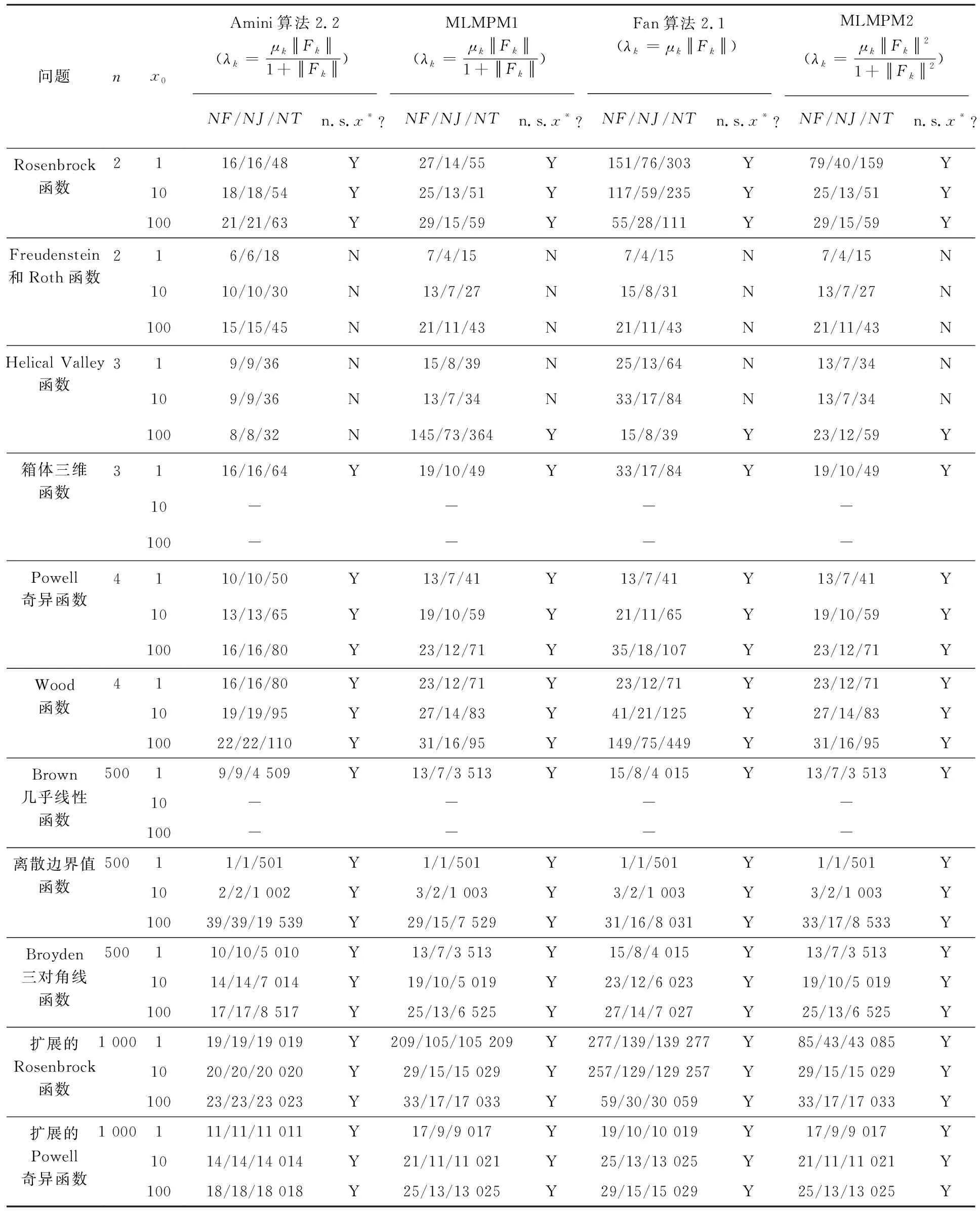
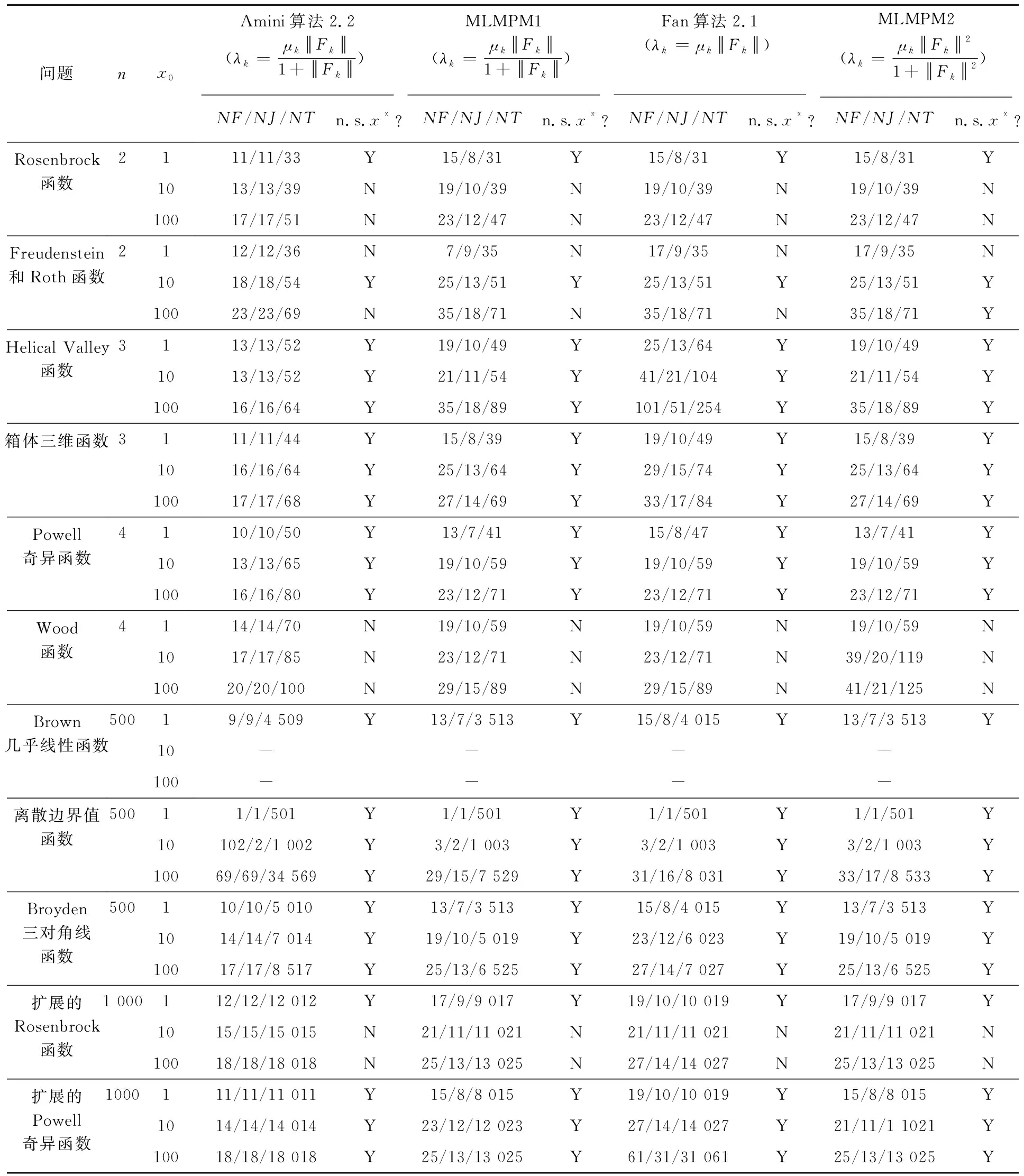
步骤1 给定x0∈Rn,0 (2.4) 计算 得到dk1. 令yk∶=xk+dk1,计算 得到dk2.记sk∶=dk1+dk2. (2.5) 步骤4令 (2.6) 步骤5令k∶=k+1,转步骤2. 由算法步骤4,易见m是μk的一个下界. 假设1F(x)连续可微且F(x)及其雅可比矩阵J(x)均Lipschitz连续,即存在常数L1>0和L2>0,使得对任意的x,y∈Rn,有 ‖F(y)-F(x)‖≤L1‖y-x‖, (3.1) ‖J(y)-J(x)‖≤L2‖y-x‖. (3.2) 易知,若(3.2)成立,则对于任意的x,y∈Rn,有 ‖F(y)-F(x)-J(x)(y-x)‖≤L2‖y-x‖2. (3.3) 引理1若Predk由(2.2)定义,则对所有的k∈N,有 Predk≥ (3.4) 该引理来自文献[9],它表明在迭代过程中预测下降量Predk总是非负的. 下面证明算法的全局收敛性. 定理1如果假设1成立,那么算法(MLMPM)要么终止于有限步,要么满足 证明反证法.假设结论不成立,则存在常数τ>0及对任意的k,有 (3.5) 定义指标集 以及成功迭代指标集 下面分两种情形进行证明. 情形1S2是有限集. 当rk μk→+∞,λk→+∞. (3.6) 从(1.5),(3.3)和(3.1),可知 (3.7) 其中常数c1>0.因此 ‖sk‖=‖dk1+dk2‖≤(1+c1)‖dk1‖. (3.8) 再结合(3.3)和(3.7),有 ‖F(xk+dk1+dk2)‖2-‖F(yk)+Jkdk2‖2= (‖F(xk+dk1+dk2)‖+‖F(yk)+Jkdk2‖)(‖F(xk+dk1+dk2)‖-‖F(yk)+Jkdk2‖)≤ (‖Fk+Jk(dk1+dk2)‖+L2‖dk1+dk2‖2+‖Fk+Jk(dk1+dk2)‖+L2‖dk1‖2)· (L2‖dk1+dk2‖2+L2‖dk1‖2)=(2‖Fk+Jk(dk1+dk2)‖+L2‖dk1+dk2‖2+ L2‖dk1‖2)(L2‖dk1+dk2‖2+L2‖dk1‖2)≤ (‖Fk+Jk(dk1+dk2)‖+O(‖dk1‖2))O(‖dk1‖2)= ‖Fk+Jk(dk1+dk2)‖O(‖dk1‖2)+O(‖dk1‖4) 以及 ‖F(yk)‖2+‖Fk+Jkdk1‖2=(‖F(yk)‖+‖Fk+Jkdk1‖)(‖F(yk)‖-‖Fk+Jkdk1‖)≤ (2‖Fk+Jkdk1‖+L2‖dk1‖2)(L2‖dk1‖2)=2L2‖Fk+Jkdk1‖‖dk1‖2+L2‖dk1‖4. 利用以上两个不等式以及(2.1)和(2.2),可推出 |Aredk-Predk|= |‖F(xk+dk1+dk2)‖2-‖F(yk)+Jkdk2‖2+‖F(yk)‖2-‖Fk+Jkdk1‖2|≤ ‖Fk+Jk(dk1+dk2)‖O(‖dk1‖2)+O(‖dk1‖4)+2L2‖Fk+Jkdk1‖‖dk1‖2+L2‖dk1‖4≤ ‖Fk‖O(‖dk1‖2)+‖Jkdk1‖O(‖dk1‖2)+‖Jkdk2‖O(‖dk1‖2)≤ ‖Fk‖O(‖dk1‖2)+‖Jkdk2‖O(‖dk1‖2). (3.9) 于是由(2.3),(3.9),(3.4),(3.1)和(3.5),有 (3.10) 情形2S2是无限集. 由引理1知‖Fk‖单调非增且有下界,由(2.3),(3.4),(3.1)和rk≥p0,可得 因此 (3.11) 由文献[12]有‖Jk‖≤L1.结合(1.2)得,当k∈S2且k→+∞时,有λk→+∞. 类似于(3.7),有 (3.12) 结合(3.11),可推出 从而由(3.1)和(3.2),以及‖Fk‖单调非增有下界,可得 dk1→0,dk2→0. 于是由(1.2),(3.5)以及‖Jk‖≤L1,可推出λk→+∞,再由(2.4)以及‖Fk‖单调非增,有 μk→+∞. (3.13) 假设由算法MLMPM生成的序列{xk}收敛于某一解x*∈X*,并作假设: 假设2F(x)连续可微,F(x)和J(x)在邻域N(x*,b),其中0 (4.1) (4.2) 因为μk≥m,故若‖Fk‖δ≤1,则有 (4.3) 若‖Fk‖δ>1,则1+‖Fk‖δ≤2‖Fk‖δ,进而有 (4.4) (4.5) (4.6) (4.7) 证明分两种情形对dk1进行讨论. 与情形1类似,有 故(4.5)得证. 接下来证明(4.6)和(4.7).从(1.2),(1.5)和(3.3),可推出 (4.8) 其中, Σk,1=diag(σk,1,…,σk,r),σk,1≥σk,2≥…≥σk,r>0, Σk,2=diag(σk,r+1,…,σk,r+q)且σk,r≥σk,r+1≥σk,r+2≥…≥σk,r+q>0. 以下为书写方便,将Σk,i,Uk,i和Vk,i(i=1,2,3)的子下标k省略,那么Jk可写成 (4.9) 由Steward和Sun[14]的矩阵扰动定理以及Jk的Lipschitz连续性,有 由此可得 (4.10) 下面分两种情形讨论. (4.11) 由于对任意σi>0(i=1,2,…,r),有 因此由Σ1的定义可推出 进而由(4.9)可得 再结合(4.8)和(4.5),即有 对所有充分大的k成立.由以上的不等式以及(4.5),有 (4.12) 又因为 所以, 结合(4.8)和(4.5),可推出 进而有 结合情形1和情形2,有(4.6)和(4.7)成立.引理得证. μk≤M. 引理3表明μk有界,其证明可见文献[9]的引理3.3. (4.13) 即,LM参数λk有上界.结合(4.3)和(4.4),可知λk有界. 下面求算法(MLMPM)的收敛阶是3.根据Jk的奇异值分解,有 (4.14) (4.15) (4.16) (4.17) (4.18) (4.19) (4.20) (4.21) 定理2若假设2成立,则由算法(MLMPM)生成的序列{xk}三阶收敛到(1.1)的某一解. 证明由(4.1),(4.2)和(3.3)可知 ‖F(yk)+Jkdk2‖+‖(J(yk)-Jk)dk2‖+L2‖dk2‖2. (4.22) (4.23) (4.24) 而对‖dk2‖,有以下两种情形. 由(4.15),(4.23),(4.19)和(4.20),可得 由(4.23),(4.19)以及(4.20),可推出 综合情形1和情形2,有 (4.25) 又由(3.2),(4.14),(4.17),(4.18),(4.24)和(4.25),有 ‖F(yk)+Jkdk2‖+‖(J(yk)-Jk)dk2‖+L2‖dk2‖2≤ 结合(4.22)可得 (4.26) 由此可推出,序列{xk}三阶收敛于解集X*. 用算法(MLMPM)对奇异非线性方程组问题进行测试,并与Amini[7]的算法2.1和Fan[9]的算法2.1进行数值结果对比.我们采用与[15]一样的问题形式,记x*是F(x)的根,将More′,Gabow和Hillstrom[16]给出的标准非奇异测试问题F(x)修改为 A∈Rn,AT=[1,…,1], 和 算法(MLMPM)的一些参数设置如下: p0=0.000 1,p1=0.25,p1=0.75,μ0=1,m=10-8,ε=10-5. 取δ=1时,记算法为MLMPM1;δ=2时,记算法为MLMPM2. n表示问题的维数; NF表示对应函数值的计算量; NJ表示对应雅可比矩阵的计算量; NT——NF+NJ*n,表示总计算量; n.s.x*?表示逻辑判断.若算法收敛到对应的非奇异问题的解x*,则记为Y,否则记为N; -表示当迭代次数达到100(n+1)时,算法不能收敛到x*. 以上测试问题均在配置i5-4200HIntel内核,2.80GHZ CPU的笔记本电脑上运行. 表1 求解rank(J(x*))=n-1的奇异非线性方程组数值结果 表2 求解rank(J(x*))=n-2的奇异非线性方程组数值结果 在上述参数设置下,表1和表2的数值结果表明,无论是对rank(J(x*))=n-1或rank(J(x*))=n-2的奇异非线性测试问题,从耗费总计算量来看,算法(MLMPM)在大部分测试问题中均优于Amini算法2.1和Fan算法2.1.尤其在n≥500的中高维问题中,MLMPM算法有较为明显的计算量优势.相较于Amini算法2.1,MLMPM中近似步的引入在一定程度上减少了雅可比矩阵的计算量;而与Fan算法2.1相比,LM参数λk的选取又具有更大的灵活性以适应迭代点xk的不同状态.此外,δ=1与δ=2的数值结果似乎相差不大.总体而言,本文提出的推广LM参数结合一个近似步的改进LM方法得到的数值结果相对较为稳定. 本文根据信赖域思想,引入推广的LM参数,进而获得一个改进的算法,该算法在每次迭代中计算一个LM步以及一个近似LM步,从而可以减少雅可比矩阵的计算量和总计算量.改进的LM算法全局收敛且具有三阶收敛速度.对一些奇异非线性方程组问题进行求解测试,初步数值结果表明该改进算法是有效的.
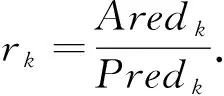
3 改进的LM算法的全局收敛性

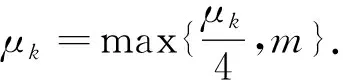
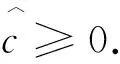
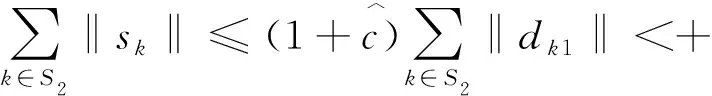

4 算法的三阶收敛性
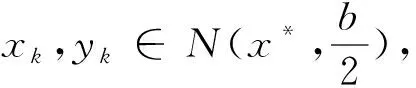
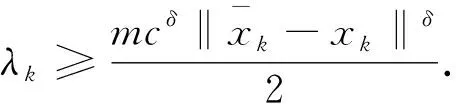
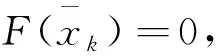
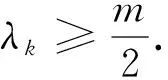
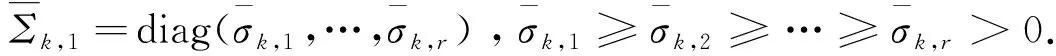
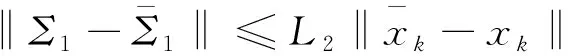
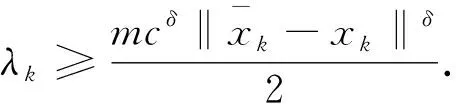
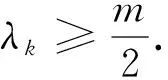
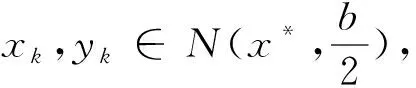
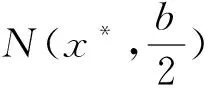
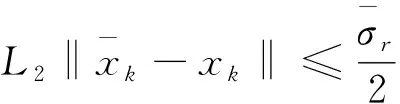
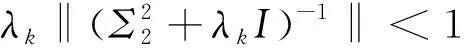
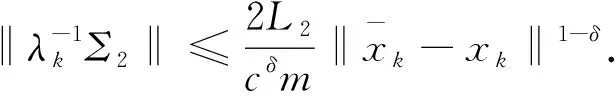
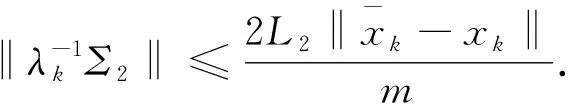

5 数值实验
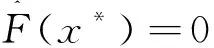
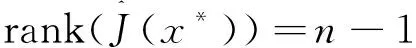
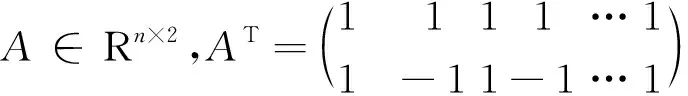

6 总结

