多项式代数上的罗巴理想*

谷伟平

(重庆人文科技学院 机电与信息工程学院， 重庆 401524)

1 引言及预备知识

罗巴代数作为一个带有罗巴算子的结合代数，是分析中积分代数的抽象和推广，起源于20世纪60年代数学家Baxter([1])关于概率论的研究，随后便得到组合学家Rota([2])等人的重视.20世纪80年代，李代数上的罗巴算子又以经典杨-巴克斯特方程的算子形式由Belavin，Drinfel′d([3])和Semenov-Tyan-Shanskii([4])各自独立发现.本世纪以来，罗巴代数的基础理论得到系统发展，在量子场论、数论、operad，Hopf 代数和组合数学等学科中有着广泛应用.与理想在代数中的地位类似,罗巴理想从根本上决定了一个罗巴代数的结构与性质.所有罗巴理想都必是通常意义上的理想,但是理想不一定是罗巴理想.因此，刻画那些恰好能成为罗巴理想的理想自然是一个非常有趣的问题,这对罗巴代数结构,特别是罗巴算子的把握具有重要意义.

域F上的多项式代数F[x]是数学上最经典的研究对象之一.2015年，Zheng,Guo 和Rosenkranz([5] )研究了F[x]上的罗巴算子与积分之间的关系.随后，Yu([6])给出了F[x]上权为零的单项式罗巴算子的分类.本文将在此基础上，刻画F[x]上单项式罗巴算子对应的罗巴理想的结构.因为F[x]是一个主理想整环,其每一个理想都由一个元素生成，所以，刻画F[x]的罗巴理想，就等价于研究哪些多项式生成的理想是罗巴理想.

下面先给出本文所需要的基本定义与符号.如不特别说明，N表示非负整数集，F表示一个特征为零的域，F[x]上的多项式f(x)有时也简记为f，集合

supp(f)={i∈N|xi在f中的系数不为零}

称为f的支撑集.其他符号和概念参见文献[7,8,9].

设R是F上的一个结合代数,λ是F中的一个元素.若R上的一个线性算子P:R→R满足等式

P(x)P(y)=P(xP(y))+P(P(x)y)+λP(xy) (x,y∈R),

则称P是R上权为λ的罗巴算子，并称(R，P)是一个权为λ的罗巴代数.若R的一个理想I满足P(I)⊆I,则称I为罗巴理想.由R的一个非空子集S生成的理想和罗巴理想分别记作〈S〉和〈S〉RB.

设P是多项式代数F[x]上的罗巴算子.若任意单项式在P下的像仍为单项式，则称P为单项式罗巴算子.因此，对任意一个单项式罗巴算子P，必有唯一的映射β∶N→F和θ∶N→N，使得P(xn)=β(n)xθ(n).显然，当β(n)=0时,θ(n)的取值是无关紧要的，所以，为了简单起见，此时规定θ(n)=0.

2 权为零的单项式罗巴算子对应的罗巴理想

这一节，主要对F[x]上权为零的单项式罗巴算子对应的罗巴理想进行分类，证明这类罗巴理想只能由单项式生成. 为了证明主要结论，首先给出一个关于罗巴代数的一般结论.

引理1设(R，P)是一个权为λ含单位元的交换罗巴代数，S是R的一个非空子集，则由S生成的罗巴理想〈S〉RB是R中由集合

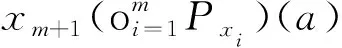
故由P的线性性可知,P(I)⊆I,从而I是由SRB生成的罗巴理想,即I=〈SRB〉RB.因为S⊆SRB⊆〈S〉RB，所以〈S〉RB=〈SRB〉RB, 从而I=〈S〉RB.

关于F[x]上罗巴理想，有以下结论.

引理2设P是F[x]上的一个权为λ的罗巴算子,则理想〈f〉是一个罗巴理想当且仅当对任意k∈N,都有f|P(xkf).

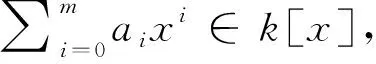
可被f整除,从而P(g)∈〈f〉,所以〈f〉是一个罗巴理想.

根据文献[6] 的定理2.9,有如下结论.

命题1设P是F[x]上的一个权为零的罗巴算子,且P(xn)=β(n)xθ(n),n∈N,则P是一个单项式罗巴算子当且仅当存在正整数d,d个非负整数c0,c1,…,cd-1以及F中的d个元素b0,b1,…,bd-1使得

(i)bi=0当且仅当ci=0,其中i=0,1,…,d-1;

(ii) 对任意n∈N,有

本节余下部分总是假设F[x]上权为零的罗巴算子P由命题1给出.记Sβ={i∈N|β(i)≠0},Sθ={i∈N|θ(i)≠0},则由命题1可知, 对于权为零的单项式罗巴算子,总有Sβ=Sθ.

引理3设f(x)是F[x]上的一个多项式,P是F[x]上由命题1定义的一个权为零的非零单项式罗巴算子.若对于满足条件0≤k≤d-1的整数k,总有P(xkf)=0,则f=0.

β(m+p)amxθ(m+p)+β(m+p+1)am+1xθ(m+p+1)+…+β(n+p)anxθ(n+p)=0.

(1)

下面我们证明对任意p+1≤j≤n-m+p,都有θ(m+j)>θ(m+p),从而有β(m+p)am=0即am=0,得到矛盾,进而完成证明.事实上,当p+1≤j≤d-1时,由M的最小性和p的最大性可知,θ(m+j)>θ(m+p)成立.当d≤j≤n-m+p时,m+j大于m,m+1,…,m+d-1并且恰好与其中的一个元素模d同余，不妨设m+j与m+μ模d同余，则存在正整数k使得m+j=m+μ+kd，所以，根据命题1中θ(n)的公式及θ(m+p)的最小性得

θ(m+j)=θ(m+μ)+kd≥θ(m+p)+kd>θ(m+p),

再结合式(1)可知,xθ(m+p)在P(xpf)中的系数β(m+p)am=0.注意到β(m+p)≠0,所以am=0，与假设矛盾.因此，f=0.

引理4设f(x)是F[x]上的一个非零多项式,P是F[x]上的一个权为零的非零单项式罗巴算子，则〈f〉是一个罗巴理想当且仅当f是一个单项式.

证明若f是一个单项式,则因为F是域,所以可以假设f的首项系数为1, 不妨令f=xm.对任意非负整数k有,P(xkf)=P(xm+k)=β(m+k)xθ(m+k).令k+m=qd+r,其中q,r∈N,0≤r≤d-1.由命题1,若β(k+m)=0,则P(xk+m)=0,从而f|P(xkf).若β(k+m)≠0,则θ(k+m)≠0,从而cr=θ(r)≥1,于是θ(k+m)=crd+qd≥r+qd=k+m≥m,因此也有f|P(xkf).从而根据引理2,〈f〉是一个罗巴理想.

反之，假设〈f〉是一个罗巴理想.由于f是一个非零多项式,所以根据引理3,必存在非负整数k,0≤k≤d-1,使得P(xkf)≠0.根据引理2,f|P(xkf),故当P(xkf)是单项式时,f必是单项式.以下假设P(xkf)不是单项式.由命题1,P(xkf)中系数不为零的单项式的幂指数必可被d整除, 所以可设

g(x)=P(xkf)=amximd+am-1xim-1d+…+a1xi1d,

其中aj≠0,j=1,2,…,m,且im>im-1>…>i1≥0.因为P≠0,所以Sβ≠Ø,从而存在s∈{0,1,…,d-1}使得bs≠0,cs≠0.于是，对任意l∈N,有

进而得到

因为P(xs+dg),P(xs+2dg),…,P(xs+mdg)都是〈f〉中的元素,所以只需证明它们的最大公因式是x的方幂,就可以保证f是一个单项式.为此,取一个包含F的代数闭域K.

令

并取以α1,α2,…,αm作为行向量组的矩阵A，则

注意到矩阵A的行列式

所以在域K上,h1=h2=…=hm=0必蕴含x=0,这说明h1,h2,…,hm的最大公因式在域K上的根只有零.由于代数闭域K上任何次数大于零的多项式都能分解为一次因式的乘积，所以h1,h2,…,hm的最大公因式必是x的方幂，从而证明了P(xs+dg),P(xs+2dg),…,P(xs+mdg)的最大公因式是x的方幂，即f是一个单项式.

定理1设P是F[x]上的一个权为零的非零单项式罗巴算子,f(x)=anxn+an-1xn-1+…+atxt是F[x]上的一个非零多项式,其中n≥t且at≠0,则〈f〉RB=〈xt〉.

证明根据引理4,F[x]的每个罗巴理想都由一个单项式生成, 所以可以假设〈f〉RB=〈xm〉, 其中m∈N.于是xm|f,从而m≤t.下面证明t≤m,从而完成证明.