基于应变模态的风机叶片损伤诊断研究
张则荣,韩桐桐,李 影
(青岛科技大学 机电工程学院,山东 青岛 266061)
0 引言
风机叶片是风力发电机中非常重要的部件,其受力较复杂,工作时承受脉动风载荷、离心惯性力载荷和重力载荷。风机全天运行且工作环境恶劣,易造成风机叶片产生腐蚀、磨损、疲劳裂纹[1]。如果不能及时修复,叶片上的疲劳裂纹会在交变应力作用下逐渐扩展至发生疲劳断裂。
风机结构的损伤会引起叶片质量、刚度和阻尼的变化,其模态频率、位移模态等参数也会相应发生变化[2]。但结构的模态频率和位移模态对损伤的敏感度较低,不能准确地对结构进行损伤辨识[3],而应变是位移的微分形式,因此在损伤诊断中,前者比后者更为敏感。文献[4]推导了应变与位移之间的关系,建立了基于应变响应的表达式及其传递矩阵。文献[5]指出,在结构产生损伤时,应变类指标要比位移类指标对损伤的出现、位置和程度更加敏感。文献[6]~[9]借助应变振型在结构损伤处产生的突变峰值分别实现了混凝土框架、管道、振动筛横梁和滑动电接触轨道的损伤辨别。文献[10]通过对损伤后的应变振型进行差分处理而建立的损伤定位指标和对未受损处的数据进行拟合而建立的损伤程度指标可以有效地识别出桥梁的受损状况。
通过对风机叶片进行模态分析,可以确定其模态频率和位移模态,而叶片的裂纹损伤会导致受损局部的刚度降低和应变模态突变。本文借助有限元软件对风机叶片进行模态分析,然后将分析得到的位移模态经微分运算得到叶片的应变模态,选取应变模态变化率作为损伤诊断指标,再通过差分运算由应变模态得到差分曲线,选取直接定位损伤指标ISMSD作为损伤指标进行对比,从而进一步确定叶片的损伤位置和裂纹损伤程度。
1 应变模态损伤识别的理论基础
风机叶片的有限元分析是把复杂的叶片划分成有限个数的微小单元,其振动动力学方程为

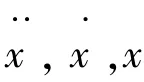
对叶片进行模态分析,系统是自由振动,无外力作用,所以F=0,且忽略阻尼的影响,则式(1)可以简化为

由 式(2)可 得:
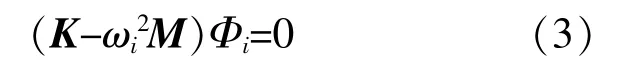
式中:ωi,Φi分别为与第i阶模态对应的模态频率和位移振型。
应变模态可由位移模态经过推导得出,其对应关系为[4]

式中:ψiε为第i阶应变模态振型;B为应变算子矩阵;D为线性微分算子;P为位移函数矩阵;A为数值矩阵;β为坐标变换矩阵。
将 式(4)代 入 式(3)可 得:
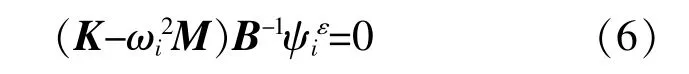
由 式(3),(6)可 知,每 一 阶 位 移 模 态 均 有 与 其相对应的应变模态,两者的模态刚度、模态频率和模态质量均相同。
风机叶片由于结构损伤而产生裂纹时,会引起结构物理参数和模态参数的变化。通常损伤对结构质量影响较小,即ΔM=0,损伤主要引起叶片损伤局部刚度降低,即式(3)变为
相应地,应变模态参数也会因位移模态参数变化而产生改变,因此由式(6)可得:
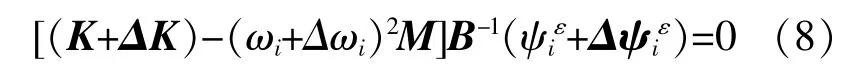
式 中:ΔK,ΔΦi,Δψiε分 别 为 叶 片 受 损 前 后 刚 度、位移模态和应变模态的变化矩阵;Δωi为受损前后模态频率的改变量。
2 风机叶片有限元模型及位移模态分析
本文的研究对象为一小型风力发电机叶片,其长度为3.9 m,材料是以环氧树脂为基体,玻璃纤维为增强体的玻璃钢,材料参数见表1。

表1 玻璃钢复合材料参数Table 1 Parameters of FRP composites
风机叶片为悬臂梁结构,在叶根处设置固定端约束,采用4节点6自由度的壳单元SHELL181建立风机叶片有限元模型(图1),共划分为18 652个节点,37 231个单元。

图1 风机叶片有限元模型Fig.1 Finite element model of wind turbine blade
风机叶片距叶根部长度30%和70%处是其疲劳裂纹萌生、扩展和易断区[11],本 文 选 取 距叶根2.7 m处(70%处)作为损伤位置,通过设置宽1 mm的穿透型横向裂纹来模拟损伤,通过设置如表2所示工况对风机叶片进行模态分析。

表2 模拟工况Table 2 Parameter of variable parameter model
利用模态分析仿真计算得到距叶根2.7 m处叶片受损前、后的五阶模态频率如表3所示。

表3 叶片受损前、后前五阶模态频率Table 3 Modal frequency before and after blade damage
对比表3中的数据可知,当发生损伤时,风机叶片的每一阶模态频率均呈现下降趋势,损伤程度越大模态频率越低,因此以叶片模态频率下降作为损伤指标可判别结构是否发生损伤,但模态频率是结构本身的固有属性,反映的是叶片整体的状态,叶片的受损位置仅凭模态频率很难确定。
图2为仿真分析得到的风机叶片位移模态振型。由图2可知:第一阶位移模态振型为挥舞;第二阶位移模态振型为摆振;第三阶为挥舞和摆振的耦合,以挥舞为主。由于振动引起的能量主要汇集在低阶模态,故对叶片结构影响最大的是第一阶挥舞和第二阶摆振位移模态。
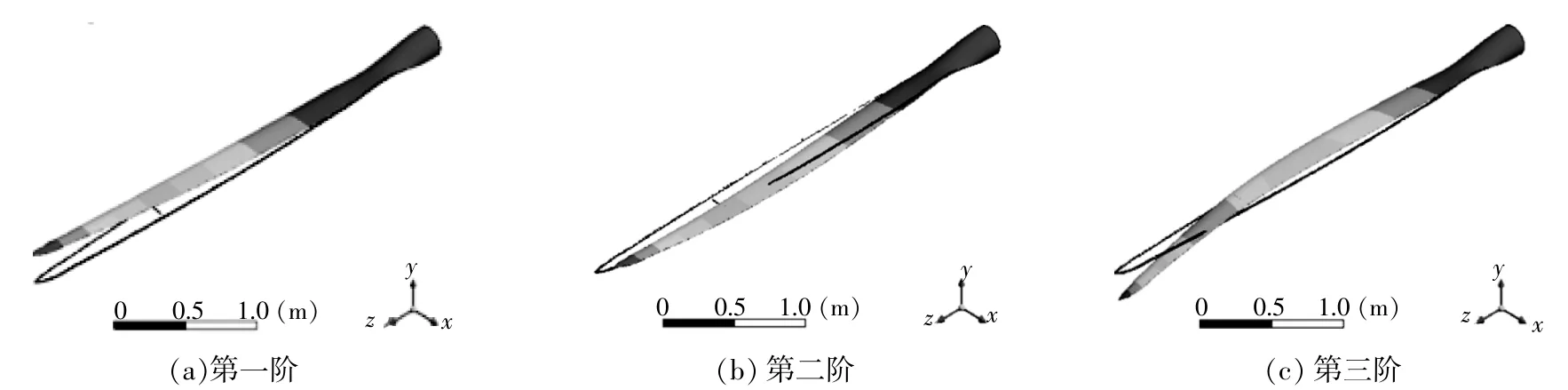
图2 叶片前三阶位移模态振型Fig.2 Displacement mode of blade
3 风机叶片应变模态分析
在风机叶片表面沿展向选取一条路径,通过该路径线来分析第一、三阶位移振型沿叶片长度挥舞振动的变化趋势。第一阶、第三阶距叶根2.7 m处分别发生10%,30%和70%损伤程度时的位移模态振型如图3所示。
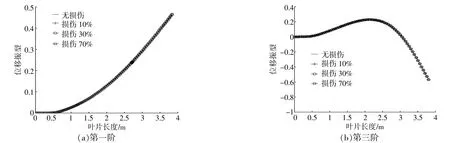
图3 2.7 m处损伤位移模态振型Fig.3 Damage displacement mode shape at 2.7 m
由图3可知,在不同损伤程度下的位移模态振型均没有因裂纹的存在而产生较为明显的突变,各位移模态振型近似汇集成一条曲线,无法判断出叶片的受损位置,故位移模态振型对受损区域的识别度较低。
相同损伤程度下的第一阶、第三阶应变模态振型如图4所示。由图4可知:第一、三阶应变模态振型均在距离叶根0.6 m处发生了突变,原因是在叶片翼型的过渡处存在应力集中现象,但该处的突变并没有因受损情况的不同而改变;应变模态振型在2.7 m受损处也产生了明显的突变,突变随着裂纹长度的增加而增大,损伤程度越大,应变模态振型在受损区域产生的突变越显著,影响的范围越广。
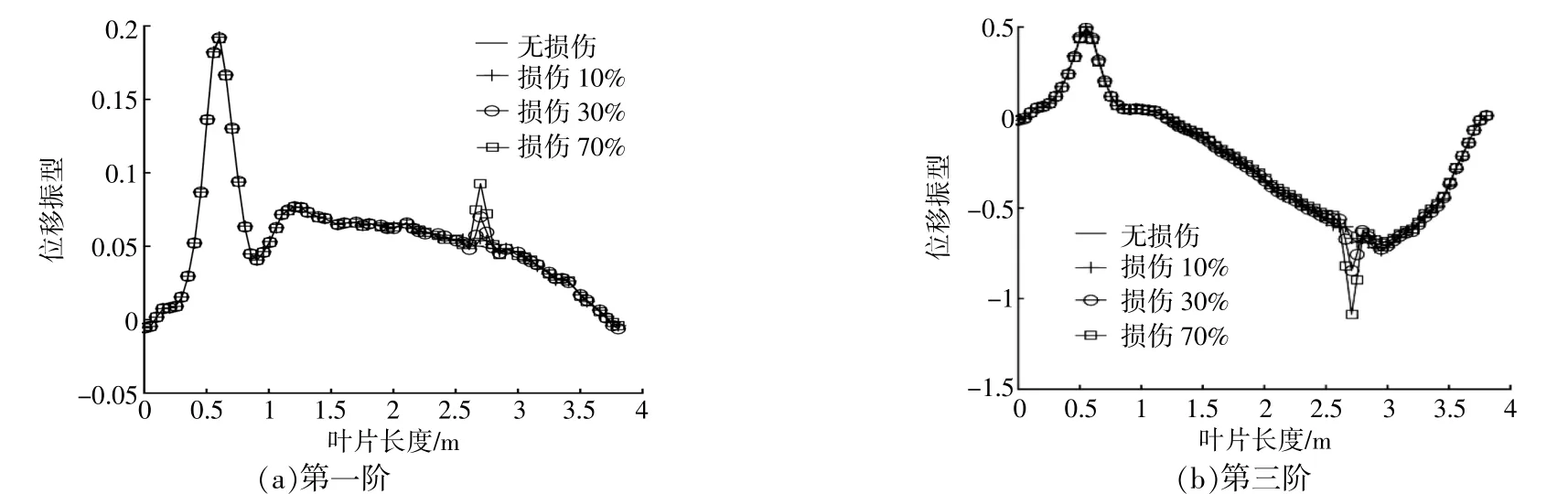
图4 2.7 m处损伤应变模态振型Fig.4 Damage strain mode at 2.7 m
风机叶片受损后其应变模态振型比模态频率和位移模态振型的突变更明显,对损伤的辨识度更高,故将应变模态变化率SR作为损伤指标,可提高损伤辨识的有效性和可靠性[7]。式中:m为选取的有效模态阶数之和;s为选取的有效模态阶数,取模态均值来提升识别效果的准确度。
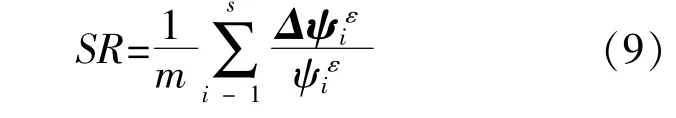
距叶根2.7 m处的SR如表4所示。

表4 2.7 m处受损时的SRTable 4 Strain mode change rate at 2.7 m
对SR与对应受损程度d的关系采用最小二乘法进行拟合,采用四次多项式拟合时,相关系数R2最小。

拟合曲线和函数关系如图5所示。

图5 拟合曲线Fig.5 Fit curve
4 基于应变模态差分曲线的损伤定位
当损伤程度较低时,应变模态振型的突变并不明显,难以观察到突变峰,且容易受到噪声的影响。而由应变模态曲线差分运算后的差分曲线建立的ISMSD对损伤量较小的情况有较好的识别效果。通过观察发现,风机叶片的应变模态振型存在一些极值点,极值点的导数为零,即应变模态振型上的极值点在差分曲线上横坐标值为零,这些点即为叶片受损处或应变模态曲线峰值处。
采用三次样条插值法对应变模态曲线进行差分 运 算,式(11)为 等 间 距 基 本 差 分 格 式,式(12),(13)为边界节点1和n处的差分格式。
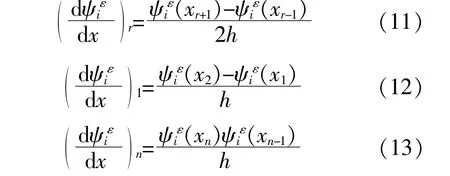
式中:h为相邻节点的间距;x为相应节点的坐标值,如xr+1为节点r+1的坐标值。
应变差分曲线进行三次样条插值时,须设置边界条件,采用第一类边界条件,其差分格式分别为
根据仿真数据微分得到的应变模态曲线,取等间距 为0.05 m,结合上述应变差分格式利用三次样条插值方法得到差分曲线(图6)。除0.6 m翼型过渡处,差分曲线仅在2.7 m受损区域产生急剧变化。
由图6可知:第一阶应变模态2.7 m处损伤差分曲线在损伤区域从左侧极大值经过受损处很快达到右侧极小值;第三阶2.7 m处损伤差分曲线在损伤区域从左侧极小值经过受损处很快达到右侧极大值,受损处的差分值有时不一定为零,这是因为损伤处于应变模态曲线上的非峰值点,但是曲线仍会在损伤处产生变化,相当于平移横向坐标轴至受损处;第一、三阶模态下10%~50%受损量下的应变模态差分曲线近似交于同一位置,其他零值点在各受损工况下基本重合在一起。尽管受损位置处差分曲线产生的突变幅度稍有差异,但无论受损状况如何,各工况下的差分曲线均交于一点,接近受损位置,故适合用作损伤定位指标。
如果差分曲线任意两个相邻极值的符号不同,它们之间只有一个零点,则该点为有效极值点,叶根和翼型过渡处之外的零值点为有效点。基于上述建立的损伤位置直接指标为


由表5,6可知:同受损量下ISMSD的值在2.7 m损伤处(表5有效零值点为l3,表6有效零值点为l4)最大,损伤程度为50%以下时,增长速度较快,超过50%以后增长变缓;在受损处两侧 的 有 效 极 值 点(表5为l2,l4,表6为l3,l5)对 应的ISMSD值变化情况类似损伤位置;非损伤位置有效 零 值 点(表5为l1,l5,表6为l1,l2和l6)的ISMSD值变化程度不大,趋于平稳。由此可以准确地确定损伤位置。第一、三阶2.7 m处受损的平均值变化如图7所示。

图7 损伤处定位指标平均值曲线Fig.7 Average value curve of damage location index
5 结论
本文借助ANSYS软件建立了长度为3.9 m的风机叶片有限元模型,在不同损伤工况下,通过比较损伤前后的模态频率、位移模态及应变模态参数,得到以下结论。
①通过对产生损伤裂纹的风机叶片进行位移模态、应变模态分析,发现叶片受损前、后的同阶模态频率变化不明显,损伤前后位移模态振型变化亦不显著,以模态频率和位移模态振型作为损伤识别指标很难对风机叶片进行损伤定位。
②风机叶片受损区域的应变模态曲线相比未受损位置产生了明显的突变峰值,据此建立了应变模态变化率损伤指标。受损程度较小时,难以在曲线上观察到明显的突变峰,但经过差分处理后的差分曲线在受损区域会产生剧烈变化,各受损程度的差分曲线近似相交于一点,不随损伤量的变化而改变。将基于应变模态差分原理的直接指标和应变模态变化率共同作为风机叶片损伤识别指标能够进一步提高识别的精确度,降低由于损伤识别误差造成的损伤误判概率。

